革命固体:洗手者制造的数量

播放段落

A solid of revolution can be created by revolving the area under a single curve around some axis, and the disk method (a form of slicing) can be used to determine the volume of the solid. If the area that is being revolved around an axis is defined by the area between two curves ( discussed in the  Concept: ), can we continue to use the slicing method to determine the volume of the solid? Does anything need to change?
::将区域旋转到某个轴周围的单一曲线下可以产生一个坚实的革命。 磁盘法(一种切片形式)可以用来确定固体的体积。 如果围绕一个轴旋转的区域是由两个曲线之间的区域(概念中的讨论: ) 来定义的 , 我们能否继续使用切片法来确定固体的体积? 有什么需要改变吗 ?

播放段落

Volumes by Washers
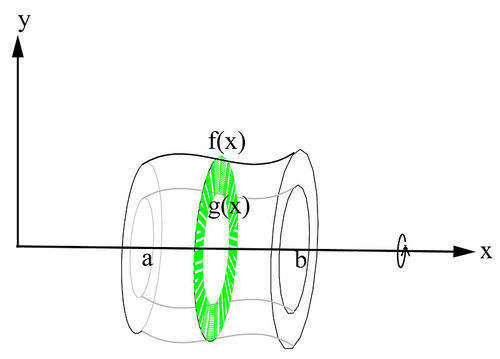
::洗涤器的体积

播放段落

Suppose that  $\begin{align*}f(x)\end{align*}$ and  $\begin{align*}g(x)\end{align*}$  are non-negative and continuous functions such that $\begin{align*}f(x) \ge g(x)\end{align*}$ for  $\begin{align*}a \le x \le b\end{align*}$ . When the region, $\begin{align*}R\end{align*}$ , enclosed by the two graphs and bounded by  $\begin{align*}x=a\end{align*}$ and  $\begin{align*}x=b\end{align*}$  is revolved about the $\begin{align*}x\end{align*}$ -axis, it will generate washer-like cross-sections in the plane perpendicular to the $\begin{align*}x\end{align*}$ -axis at each $\begin{align*}x\end{align*}$ , as shown in the figures.
::假设f(x)和g(x)是非负性和连续性的函数,例如,f(x)g(x)x(x)xxb。当区域R(由两个图表附着,并被 x=a 和 x=b 捆绑)围绕x轴旋转时,如图所示,它会在平面中产生与每个xx轴垂直的类似异形横截面。

播放段落

At each value of  $\begin{align*}x\end{align*}$ in the interval $\begin{align*}[a,b]\end{align*}$ , there will be two radii: an inner radius  $\begin{align*}g(x)\end{align*}$ and an outer radius. The area of each washer in the plane perpendicular to the $\begin{align*}x\end{align*}$ -axis is $\begin{align*}(\pi[f(x)]^2-\pi[g(x)]^2)\end{align*}$ , and can be projected a distance $\begin{align*}dx\end{align*}$  along the $\begin{align*}x\end{align*}$ -axis to create an incremental piece of the solid’s volume. The total volume of the solid of revolution in the interval  $\begin{align*}[a,b]\end{align*}$ is then given by:
::在[a,b] 间隔期间, x 的每个值将有两个半径: 内半径 g(x) 和外部半径。 与 x 轴垂直的平面上每个隔热层的面积为( {[f(x)] 2] {[g(x)] 2] , 并可以预测 x 轴沿线的距离 dx , 以创建固体体积的递增部分。 然后给出在间隔[a,b] 间隔内革命的固体总量 :

播放段落

$$\begin{align*}V=\int\limits_a^b \pi([f(x)]^2-[g(x)]^2)dx.\end{align*}$$
::V=ba([f(x)]2-[g(x)]2)dx。

播放段落

Apply the equation  from above and find the volume generated when the region between the graphs $\begin{align*}f(x)=x^2+1\end{align*}$  and $\begin{align*}g(x)=x\end{align*}$  over the interval [0, 3] is revolved about the $\begin{align*}x\end{align*}$ -axis.
::从上方应用方程式, 并查找在图形 f( x) =x2+1 和 g( x) =x 间距 [ 0, 3] 之间的区域围绕 x 轴旋转时生成的音量 。

播放段落

Because the revolution is about the $\begin{align*}x\end{align*}$ -axis, the volume is determined as follows:
::由于革命是关于X轴的,其体积确定如下:

播放段落

V ( x ) = b ∫ a π ( [ f ( x ) ] 2 − [ g ( x ) ] 2 ) d x = 3 ∫ 0 π ( ( x 2 + 1 ) 2 − ( x ) 2 ) d x = 3 ∫ 0 π ( x 4 + x 2 + 1 ) d x = 303 π 5 .

$$\begin{align*}V(x) &=\int\limits_a^b \pi([f(x)]^2-[g(x)]^2)dx \\ &=\int\limits_0^3 \pi((x^2+1)^2-(x)^2)dx \\ &=\int\limits_0^3 \pi(x^4+x^2+1)dx \\ &=\frac{303 \pi}{5}.\end{align*}$$
::V(x) = ba}([f(x)]2 - [g(x)] 2) dx= 30((x2+1) 2-(x) 2) dx= 30(x4+x2+1) dx=303}5) (x4+x2+1) (x=303}5) (x2+1) (x2+1)

播放段落

What if the region enclosed by the two curves "> $\begin{align*}w(y)\end{align*}$  and  "> $\begin{align*}v(y)\end{align*}$ generates washers in planes perpendicular to the $\begin{align*}y\end{align*}$ -axis when it is revolved about the $\begin{align*}y\end{align*}$ -axis? In an analogous construction as for revolution about the $\begin{align*}x\end{align*}$ -axis, if  "> $\begin{align*}w(y)\end{align*}$  and  "> $\begin{align*}v(y)\end{align*}$ are non-negative and continuous functions such that %20%5Cge%20v"> $\begin{align*}w(y) \ge v(y)\end{align*}$  for $\begin{align*}c \le y \le d\end{align*}$ , the volume of this solid is given by:
::如果两个曲线和 v所覆盖的区域在围绕 Y 轴旋转时产生与y 轴垂直的平面上的洗衣液呢? 在类似X 轴革命的构造中,如果 w和 v是非负和连续的函数,例如cv,则该固体的体积如下:

播放段落

%5D%5E2-%5Bv%5D%5E2)dy."> V = d ∫ c π ( [ w ( y ) ] 2 − [ v ( y ) ] 2 ) d y .

$$\begin{align*}V=\int\limits_c^d \pi([w(y)]^2-[v(y)]^2)dy.\end{align*}$$

::V=dc([w]2 -[v]2] dy。

播放段落

Apply the equation from above and find the volume of the solid generated by revolving the region bounded by $\begin{align*}f(x)=2-x^2\end{align*}$ , $\begin{align*}g(x)=\sqrt{1-x^2}\end{align*}$ , $\begin{align*}x=0.25\end{align*}$ , and $\begin{align*}y=0\end{align*}$  about the $\begin{align*}y\end{align*}$ -axis.
::应用上面的方程式, 并找到以 f( x) =2 - x2, g( x) =1 - x2, x=0. 25, y=0 有关 Y 轴的区域旋转产生的固体体积 。

播放段落

The figure below shows the cross-section in the $\begin{align*}xy\end{align*}$ -plane of the solid of revolution generated by revolving the shaded region in Quadrant I about the $\begin{align*}y\end{align*}$ -axis .
::下图显示了在Quadrant I关于y轴轴的阴影地区旋转所产生的革命固体的x-平面的横截面。

播放段落

Because the revolution is about the $\begin{align*}y\end{align*}$ -axis, the volume is determined by the general integral:
::因为革命是关于Y轴的, 音量是由整体整体决定的:

播放段落

%5D%5E2-%5Bv%5D%5E2)dy."> V = d ∫ c π ( [ w ( y ) ] 2 − [ v ( y ) ] 2 ) d y .

$$\begin{align*}V=\int\limits_c^d \pi([w(y)]^2-[v(y)]^2)dy.\end{align*}$$
::V=dc([w]2 -[v]2] dy。

播放段落

The plane of each washer with thickness $\begin{align*}dy\end{align*}$  is perpendicualr to the $\begin{align*}y\end{align*}$ -axis. The interval of integration is from $\begin{align*}y=0\end{align*}$ to $\begin{align*}y=2\end{align*}$ . However, examination of the figure shows that the interval of integration along the $\begin{align*}y\end{align*}$ -axis needs to be broken up into two sub-intervals to account for the change of the function  "> $\begin{align*}v(y)\end{align*}$ as follows:
::厚度为y 轴的每张隔板的厚度为 Y 轴的近距离。 集成间隔从 y=0 到 y=2 。 然而,对图的检查表明, Y 轴的集成间隔需要分为两个次间隔,以说明函数 v 的变化如下:

播放段落

$\begin{align*}y\end{align*}$ -sub-interval $\begin{align*}1 = [0,1]\end{align*}$ : %3D%5Csqrt%7B2-y%7D"> $\begin{align*}w(y)=\sqrt{2-y}\end{align*}$ , the inverse of $\begin{align*}f(x)\end{align*}$ , and %3D%5Csqrt%7B1-y%5E2%7D"> $\begin{align*}v(y)=\sqrt{1-y^2}\end{align*}$ , the inverse of $\begin{align*}g(x)\end{align*}$ ; and
::y-sub-interval 1 = [0,1]: w%%2-y, f(x) 和 v%1-y2 的反义, g(x) 的反义;以及

播放段落

$\begin{align*}y\end{align*}$ -sub-interval $\begin{align*}2 = [1,2]\end{align*}$ : %3D%5Csqrt%7B2-y%7D"> $\begin{align*}w(y)=\sqrt{2-y}\end{align*}$  and %3D0.25"> $\begin{align*}v(y)=0.25\end{align*}$ .
::y-sub-interval 2=[1,2]: w2-y和v=0.25。

播放段落

With this in mind, the volume is evaluated as follows:
::考虑到这一点,对该卷的评价如下:

播放段落

%5D%5E2-%5Bv%5D%5E2)dy.%20%5C%5C%0A%26%3D%5Cint%5Climits_0%5E1%20%5Cpi%20%5Cleft(%5B%5Csqrt%7B2-y%7D%5D%5E2-%5B%5Csqrt%7B1-y%5E2%7D%5D%5E2%5Cright)dy%2B%20%5Cint%5Climits_1%5E2%20%5Cpi%20%5Cleft(%5B%5Csqrt%7B2-y%7D%5D%5E2-%5B0.25%5D%5E2%5Cright)dy%20%5C%5C%0A%26%3D%5Cint%5Climits_0%5E1%20%5Cpi(y%5E2-y%2B1)dy%2B%20%5Cint%5Climits_1%5E2%20%5Cpi%5Cleft(-y%2B%20%5Cfrac%7B31%7D%7B16%7D%20%5Cright)dy%20%5C%5C%0A%26%3D%5Cpi%20%5Cleft%5B%5Cfrac%7By%5E3%7D%7B3%7D-%20%5Cfrac%7By%5E2%7D%7B2%7D%2By%20%5Cright%5D_0%5E1%2B%20%5Cpi%5Cleft%5B-%20%5Cfrac%7By%5E2%7D%7B2%7D%2B%20%5Cfrac%7B31%7D%7B16%7Dy%20%5Cright%5D_1%5E2%20%5C%5C%0A%26%3D%5Cpi%5Cleft%5B%5Cfrac%7B5%7D%7B6%7D%5Cright%5D%2B%20%5Cpi%5Cleft%5B%5Cfrac%7B7%7D%7B16%7D%20%5Cright%5D%20%5C%5C%0AV%26%3D%5Cfrac%7B61%7D%7B48%7D%20%5Cpi">

$$\begin{align*}v &=\int\limits_c^d \pi ([w(y)]^2-[v(y)]^2)dy. \\ &=\int\limits_0^1 \pi \left([\sqrt{2-y}]^2-[\sqrt{1-y^2}]^2\right)dy+ \int\limits_1^2 \pi \left([\sqrt{2-y}]^2-[0.25]^2\right)dy \\ &=\int\limits_0^1 \pi(y^2-y+1)dy+ \int\limits_1^2 \pi\left(-y+ \frac{31}{16} \right)dy \\ &=\pi \left[\frac{y^3}{3}- \frac{y^2}{2}+y \right]_0^1+ \pi\left[- \frac{y^2}{2}+ \frac{31}{16}y \right]_1^2 \\ &=\pi\left[\frac{5}{6}\right]+ \pi\left[\frac{7}{16} \right] \\ V&=\frac{61}{48} \pi\end{align*}$$
::=======================================================================================================================================================================================================

播放段落

The volume of the solid is $\begin{align*}\frac{61}{48}\pi\end{align*}$  cubic units.
::固体的体积为6148立方单位。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked whether we can continue to use the slicing method to determine the volume of the solid generated from revolving the area between two curves around an axis. Does anything need to change? If you said that the methods should not be very different, you were correct. The washer method discussed in this concept is just another application of the method of slicing. But, the shape of the slice is a disk with a hole in the middle, i.e., a washer. What changes is that we use the formula for the area of a washer to find the volume, instead of using the area of a disk.
::早些时候,有人问您,我们是否可以继续使用切片方法来确定在轴周围两个曲线之间旋转区域产生的固体体积。 需要改变什么吗? 如果您说方法不应该非常不同, 您是对的。 这个概念中讨论的洗涤方法只是切片方法的另一种应用。 但是, 切片的形状是一个圆盘, 中间有一个洞, 即一个洗衣工。 我们用洗衣工的公式来寻找这个体积, 而不是使用磁盘的面积, 有何改变 。

播放段落

Example 2
::例2

播放段落

Find the volume of the solid generated by revolving the region bounded by $\begin{align*}f(x)=2-x^2\end{align*}$ , $\begin{align*}g(x)=\sqrt{1-x^2}\end{align*}$ , $\begin{align*}x=-1\end{align*}$ , and $\begin{align*}x=1\end{align*}$  about the $\begin{align*}x\end{align*}$ -axis.
::查找以 f(x) =2 - x2, g(x) =1 - x2, x*1, 和 x=1为界于 x 轴的区域的旋转产生的固体体积。

播放段落

Because the revolution is about the $\begin{align*}x\end{align*}$ -axis, the volume is determined as follows: $\begin{align*}V=\int\limits_{a}^{b}\pi([f(x)]^2-[g(x)]^2)dx.\end{align*}$
::由于革命是有关 x 轴的, 音量确定如下 : V=ba( [f(x)]2 - [g(x)]2]dx 。

播放段落

$$\begin{align*}V &=\int\limits_a^b \pi([f(x)]^2-[g(x)]^2)dx. \\ &=\int\limits_{-1}^1 \pi \left([2-x^2]^2-[\sqrt{1-x^2}]^2\right)dx. \\ &=\pi\int\limits_{-1}^1 ([4-4x^2+x^4]-[1-x^2])dx. \\ &=\pi\int\limits_{-1}^1 [x^4-3x^2+3]dx. \\ &=\pi\left[\frac{x^5}{5}-x^3+3x \right]_{-1}^1 \\ &=\frac{22}{5} \pi\end{align*}$$
::V=b*a}([f(x)]2-[g(x)]2]2-[g(x)]2]2dx.=1*1*1}([2-x2]2-2)-2-[一至x2]2],dx.1([4-4x2+x4]-[1至x2])),dx.*1*1[x4-3x2+3],dx.[x55-x3+3x]1-1=225}

播放段落

The volume of the solid is $\begin{align*}\frac{22}{5}\pi\end{align*}$  cubic units.
::固体体积为225立方单位。

播放段落

Example 3
::例3

播放段落

Find the volume of the solid generated by revolving the region bounded by $\begin{align*}y=\sin \frac{x}{2}\end{align*}$  and  $\begin{align*}y=\cos \frac{x}{2}\end{align*}$ on the interval $\begin{align*}\left[0,\frac{\pi}{2}\right]\end{align*}$ , about the $\begin{align*}x\end{align*}$ -axis.
::查找以 y=sinx2 和 y=cosx2 的间隔 [0]2] 围绕 x 轴旋转区域产生的固体体积。

播放段落

The figure below shows the bounded region in Quadrant I that is to be revolved about the $\begin{align*}x\end{align*}$ -axis.
::下图显示Quadrant I的接壤区域,该区域将围绕x轴进行。

播放段落

Because the revolution is about the $\begin{align*}x\end{align*}$ -axis, the volume is determined as follows:
::由于革命是关于X轴的,其体积确定如下:

播放段落

$$\begin{align*}V&=\int\limits_a^b \pi([f(x)]^2-[g(x)]^2)dx. \\ &=\int\limits_0^{\frac{\pi}{2}} \pi \left(\left[\cos \frac{x}{2} \right]^2- \left[\sin \frac{x}{2} \right]^2 \right)dx. \\ &=\int\limits_0^{\frac{\pi}{2}} \pi \left(\left[1- \sin^2 \frac{x}{2} \right]- \left[\sin^2 \frac{x}{2} \right] \right)dx. \\ &=\int\limits_0^{\frac{\pi}{2}} \pi \left(1-2 \sin^2 \frac{x}{2} \right)dx. \\ &=\int\limits_0^{\frac{\pi}{2}} \pi \left(\cos x \right)dx. \quad \ldots \text{Use the trig identify} \\ &=\pi[\sin x]_0^{\frac{\pi}{2}} \\ &=\pi\end{align*}$$
::V=b*a}([f(x)]2 -[g(x)]2]]dx.202([cosx2]2-2-[sinx2]2]dx.20([1-sin2x2]-[sin2x2]))dx.20(1-2sin2x2)dx.20(cosx)dx.

播放段落

The volume of the solid is $\begin{align*}\pi\end{align*}$  cubic units.
::固体的体积是立方单位 。

播放段落

Review
::回顾

播放段落

For #1-4, find the volume of the solid generated by revolving the region bounded by the curves about the $\begin{align*}x\end{align*}$ -axis.
::在 # 1-4 中, 找到通过旋转生成的固体体积, 以 X 轴的曲线为界的区域为界 。

播放段落
1. $\begin{align*}y=\sqrt{9-x^2}\end{align*}$ , $\begin{align*}y=0\end{align*}$
   ::y9 - x2, y=0
播放段落
2. $\begin{align*}y=3+x\end{align*}$ , $\begin{align*}y=1+x^2\end{align*}$
   ::y=3+x,y=1+x2 y=3+x,y=1+x2
播放段落
3. $\begin{align*}y=\sec \ x, y=\sqrt{2}, \frac{-\pi}{4} \le x \le \frac{\pi}{4}\end{align*}$
   ::y=sec x,y2,4x4
播放段落
4. $\begin{align*}y=1\end{align*}$ , $\begin{align*}y=x\end{align*}$ , $\begin{align*}x=0\end{align*}$
   ::y=1, y=x, x=0 y=1, y=x, x=0

播放段落

For #5-8, find the volume of the solid generated by revolving the region bounded by the curves about the $\begin{align*}y\end{align*}$ -axis.
::对于5-8号, 找到圆圈产生的固体的体积, 以Y轴曲线为界的区域为界 。

播放段落
5. $\begin{align*}y=x^3\end{align*}$ , $\begin{align*}x=0\end{align*}$ , $\begin{align*}y=1\end{align*}$
   ::y=x3, x=0, y=1 y=1
播放段落
6. $\begin{align*}x=y^2\end{align*}$ , $\begin{align*}y=x-2\end{align*}$
   ::x=y2, y=x- 2
播放段落
7. $\begin{align*}x=\csc \ y\end{align*}$ , $\begin{align*}y=\frac{\pi}{4}\end{align*}$ , $\begin{align*}y=\frac{3 \pi}{4}\end{align*}$ , $\begin{align*}x=0\end{align*}$
   ::x=csc y, y4, y= 34, x=0
播放段落
8. $\begin{align*}y=0\end{align*}$ , $\begin{align*}y=\sqrt{x}\end{align*}$ , $\begin{align*}x=4\end{align*}$
   ::y=0,yx, x=4

播放段落

For #9-12, use washers  to find the volume generated when the region bounded by the curves is revolved about the axis indicated.
::对于# 9-12, 使用洗衣机寻找被曲线覆盖的区域围绕所示轴旋转时产生的体积 。

播放段落
9. $\begin{align*}y=\frac{1}{x}\end{align*}$ , $\begin{align*}y=0\end{align*}$ , $\begin{align*}x=1\end{align*}$ , $\begin{align*}x=3\end{align*}$ , about the $\begin{align*}y\end{align*}$ -axis.
   ::y=1x,y=0, x=1, x=3,关于y轴。
播放段落
10. $\begin{align*}y=x^2\end{align*}$ ,  $\begin{align*}x=1\end{align*}$ , $\begin{align*}y=0\end{align*}$ , about the $\begin{align*}x\end{align*}$ -axis.
    ::y=x2, x=1, y=0, 关于 x 轴。
播放段落
11. $\begin{align*}y=2x-1\end{align*}$ ,  $\begin{align*}y=-2x+3\end{align*}$ , $\begin{align*}x=2\end{align*}$ , about the $\begin{align*}y\end{align*}$ -axis.
    ::y=2x- 1, y2x+3, x=2, 有关 Y 轴。
播放段落
12. $\begin{align*}y^2=x\end{align*}$ ,  $\begin{align*}y=1\end{align*}$ ,  $\begin{align*}x=0\end{align*}$ , about the $\begin{align*}x\end{align*}$ -axis.
    ::y2=x, y=1, x=0, 关于 x 轴 。
播放段落
13. Use the volume by washers  method to find the volume generated when the region is bounded by  $\begin{align*}y=x^3\end{align*}$ ,  $\begin{align*}y=1\end{align*}$ ,  $\begin{align*}x=0\end{align*}$ , is revolved about the line $\begin{align*}y=1\end{align*}$ .
    ::使用洗衣机的体积方法查找当区域被y=x3、y=1、x=0捆绑时产生的体积,该体积围绕y=1线旋转。
播放段落
14. Find the volume of the solid generated by rotating about the $\begin{align*}x\end{align*}$ -axis the area between the curves  $\begin{align*}y=-2x^2+ \frac{7}{2}\end{align*}$ and $\begin{align*}y=-\frac{1}{2}x^2+2\end{align*}$ .
    ::查找在 x 轴上旋转生成的固体的体积。 在 y 2x2+72 和 y 12x2+2 之间的曲线区域中, 以 y 2x2+2 旋转生成的固体体积。
播放段落
15. Find the volume of the solid generated by rotating about the line  $\begin{align*}x=4\end{align*}$ the area between the curves $\begin{align*}x=2\end{align*}$ , $\begin{align*}y=\sqrt{x-1}\end{align*}$ , and the $\begin{align*}x\end{align*}$ -axis.
    ::在 x=4 线上旋转产生的固体的体积、曲线 x=2 、 yx-1 和 x 轴之间的区域。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

 

播放段落

Resources
::资源