节: 革命的固体:圆柱壳的体积 | 6.5 革命固体:圆柱壳壳体积

章节大纲

The method of computing volumes so far depended upon computing the cross-sectional area of the solid and then integrating it across the solid. What happens when the cross-sectional area cannot be found or the integration is too difficult to solve? Here is where the shell method comes along.
::到目前为止,计算体积的方法取决于对固体的跨部门区域进行计算,然后将其整合到整个固体中。当无法找到跨部门区域或集成太难解决时会发生什么情况?这里是罐壳方法的形成地。

Volumes by Cylindrical Shell
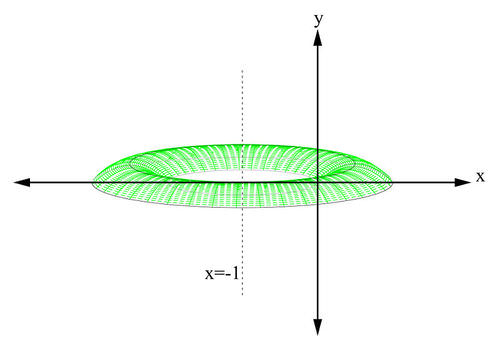
::圆柱形壳壳体积

To show how difficult it sometimes is to use the disk or the washer methods to compute volumes, consider the region enclosed by the function $\begin{aligned} f (x) = x - x^{2} \end{aligned}$ . Let us revolve it about the line $\begin{aligned} x = - 1 \end{aligned}$ to generate the shape of a doughnut-shaped cake. What is the volume of this solid?
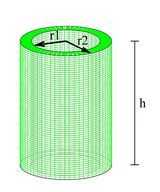
::要显示有时使用磁盘或洗衣机计算音量的方法有多困难, 请考虑函数 f( x) =x- x2. 所连接的区域。让我们绕行 x1 来生成甜甜圈形蛋糕的形状。这个固体的体积是多少 ?

If we wish to integrate with respect to the $\begin{aligned} y \end{aligned}$ -axis, we have to solve for $\begin{aligned} x \end{aligned}$ in terms of $\begin{aligned} y \end{aligned}$ . That would not be easy (try it!). An easier way is to integrate with respect to the $\begin{aligned} x \end{aligned}$ -axis by using the shell method. Here is how: A cylindrical shell is a solid enclosed by two concentric cylinders. If the inner radius is $\begin{aligned} r_{1} \end{aligned}$ and the outer one is $\begin{aligned} r_{2} \end{aligned}$ with both of height $\begin{aligned} h \end{aligned}$ , then the volume is as depicted.
::如果要结合 Y 轴, 我们就必须用y 来解析 x 。这并不容易( 尝试它! ! ) 。比较容易的方法是使用 shell 方法来整合 x 轴。下面是 : 圆柱形外壳是两个同心圆筒的固固体。如果内半径是 r1, 外半径是 r2, 两者均高 h , 则其体积是描述的。

Notice however that $\begin{aligned} (r_{2} - r_{1}) \end{aligned}$ is the thickness of the shell and $\begin{aligned} \frac{1}{2} (r_{2} + r_{1}) \end{aligned}$ is the average radius of the shell.
::然而,通知(r2-r1)是罐壳厚度,12(r2+r1)是罐壳的平均半径。

Thus
::因此,

$\begin{aligned} V = 2 π \cdot [average radius] \cdot [height] \cdot [thickness] \end{aligned}$ .
::V=2[平均半径] [高 [重。

Replacing the average radius with a single variable $\begin{aligned} r \end{aligned}$ and using $\begin{aligned} h \end{aligned}$ for the height, we have $\begin{aligned} V = 2 π \cdot r \cdot h \cdot [thickness] \end{aligned}$ .
::将平均半径替换为单变量 r , 并使用 h 来替换高度, 我们有 V=2\\\\\\\\\\\[thickness] 。

In general the shell’s thickness will be $\begin{aligned} d x \end{aligned}$ or $\begin{aligned} d y \end{aligned}$ depending on the axis of revolution. This discussion leads to the following formulas for rotation about an axis. We will then use this formula to compute the volume $\begin{aligned} V \end{aligned}$ of the solid of revolution that is generated by revolving the region about the $\begin{aligned} x \end{aligned}$ -axis.
::一般来说,罐壳的厚度是 dx 或 dy , 取决于革命的轴。这一讨论引出一个轴的旋转公式如下。然后我们将使用这个公式来计算在X轴上旋转区域所产生的革命固体的V 体积。

Suppose $\begin{aligned} f \end{aligned}$ is a continuous function in the interval $\begin{aligned} [a, b] \end{aligned}$ and the region $\begin{aligned} R \end{aligned}$ is bounded above by $\begin{aligned} y = f (x) \end{aligned}$ and below by the $\begin{aligned} x \end{aligned}$ -axis, and on the sides by the lines $\begin{aligned} x = a \end{aligned}$ and $\begin{aligned} x = b \end{aligned}$ . If $\begin{aligned} R \end{aligned}$ is rotated around the $\begin{aligned} y \end{aligned}$ -axis, then the cylinders are vertical, with $\begin{aligned} r = x \end{aligned}$ and $\begin{aligned} h = f (x) \end{aligned}$ . The volume of the solid is given by
$\begin{aligned} V = \int_{a}^{b} 2 π r h d x = \int_{b}^{a} 2 π x f (x) d x . \end{aligned}$

::假设 f 是间隔 [a, b] 的连续函数, R 区域受 y = f (x) 和 x 轴的 y = f (x) 与 y = f (x) 的区域的约束, 边上则受 x 轴的 y = a 和 x = b 。如果 R 围绕 y 轴旋转, 那么圆筒是垂直的, 包括 r=x 和 h= f (x) 。固体的体积由 Vab2rhdx ba2x (x) dx 给出。

Use the cylindrical shell method to find the volume of the solid formed by revolving the region in Quadrant I bounded by $\begin{aligned} f (x) = x - x^{2} \end{aligned}$ and $\begin{aligned} y = 0 \end{aligned}$ about $\begin{aligned} x = - 1 \end{aligned}$ .
::使用圆柱形外壳方法查找在Quadrant I 区域旋转形成的固体体积,该区域由 f(x) =x-x2 和 y= 0 约x @ @% 1 约束。

By using the volume formulation presented above, the volume of the solid of revolution is determined as:
::通过使用上述体积配方,确定革命固体的体积如下:

$\begin{aligned} V & = \int_{a}^{b} 2 π r h d x = \int_{b}^{a} 2 π r f (x) d x \\ = \int_{0}^{1} 2 π (x + 1) (x - x^{2}) d x \\ = 2 π \int_{0}^{1} (- x^{3} + x) d x \\ = 2 π {[- \frac{x^{4}}{4} + \frac{x^{2}}{2}]}_{0}^{1} \\ = \frac{π}{2} \end{aligned}$

::Vab2rhdxba2rf(x)dx012(x+1)(x-x2x)dx=201(-x3+x)dx=2[-x44+x22]01#2

The volume of the solid is therefore $\begin{aligned} \frac{π}{2} \end{aligned}$ cubic units.
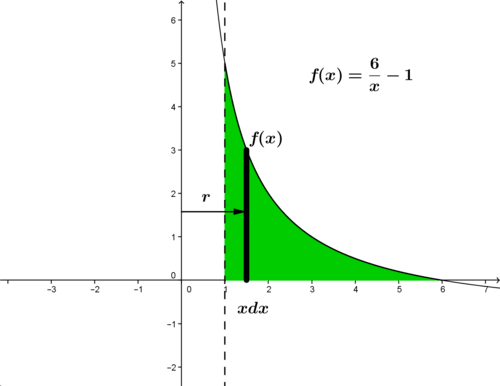
::因此,固体的体积为%2立方单位。

Use the cylindrical shell method to find the volume generated by revolving the region bounded by $\begin{aligned} x = 1 \end{aligned}$ , the $\begin{aligned} x \end{aligned}$ -axis, and $\begin{aligned} y = \frac{6}{x} - 1 \end{aligned}$ about the $\begin{aligned} y \end{aligned}$ -axis.
::使用圆柱形外壳方法查找由 x=1 、 x 轴和 y= 6x- 1 围绕 y 轴区域旋转产生的体积。

By using the volume formulation presented above, the volume of the solid of revolution is determined as:
::通过使用上述体积配方,确定革命固体的体积如下:

$\begin{aligned} V & = \int_{a}^{b} 2 π r h d x = \int_{b}^{a} 2 π r f (x) d x \\ = \int_{1}^{6} 2 π (x) (\frac{6}{x} - 1) d x \\ = 2 π \int_{1}^{6} (6 - x) d x \\ = 2 π {[6 x - \frac{x^{2}}{2}]}_{1}^{6} \\ = 25 π \end{aligned}$

::Vab2rhdxba2rf(x)dx_162}(x)6x-1)dx=216(6-x)dx=2}[6x-x22]16=25}[6x-x22]16=25}

The volume of the solid is therefore $\begin{aligned} \frac{π}{2} \end{aligned}$ cubic units.
::因此,固体的体积为%2立方单位。

The previous examples looked at solids generated by revolving some region about the $\begin{aligned} y \end{aligned}$ -axis, or some other vertical axis. Equivalently, if the volume is generated by revolving the same region about the $\begin{aligned} x \end{aligned}$ -axis, then the cylinders are horizontal with
::前几个例子考察了一些区域围绕 Y 轴或一些其他垂直轴旋转产生的固体。同样,如果该体体是由同一区域围绕 X 轴旋转产生的,那么圆筒是水平的,

$\begin{aligned} V = \int_{c}^{d} 2 π r h d y, \end{aligned}$

::

where $\begin{aligned} c = f^{- 1} (a) \end{aligned}$ and $\begin{aligned} d = f^{- 1} (b) \end{aligned}$ . The values of $\begin{aligned} r \end{aligned}$ and $\begin{aligned} h \end{aligned}$ are determined from the context of the problem.
::其中 c=f-1(a) 和 d=f-1(b) 。 r 和 h 的值根据问题的背景确定。

Examples
::实例

Example 1
::例1

Earlier, you were asked what to do when the cross-section cannot be found or the integration is too difficult. When the disk or washer method is employed and the cross-sectional area of a solid of revolution cannot be found (or the integration is too difficult to solve), the cylindrical shell method is often the way to go. Remember that the cylindrical strips will be parallel to the axis of rotation and the integration along the axis perpendicular to the axis of rotation
::早些时候,有人询问您在无法找到横截截面或整合过于困难时要做什么。当磁盘或洗衣机方法被使用,无法找到革命固体的跨截面区域(或整合太难以解决)时,圆柱体外壳方法往往是前进的道路。要记住圆柱体内带将与旋转轴平行,圆轴的整合与旋转轴垂直平行。

Example 2
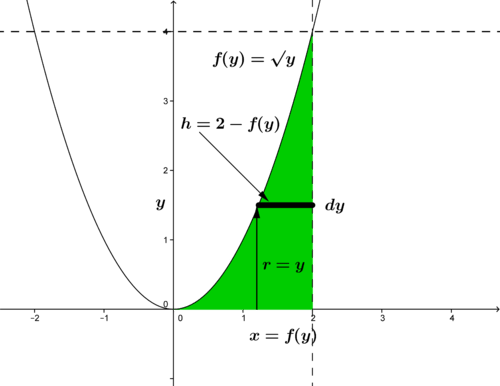
::例2

A solid figure is created by rotating the region $\begin{aligned} R \end{aligned}$ around the $\begin{aligned} x \end{aligned}$ -axis. $\begin{aligned} R \end{aligned}$ is bounded by the curve $\begin{aligned} y = x^{2} \end{aligned}$ and the lines $\begin{aligned} x = 0 \end{aligned}$ and $\begin{aligned} x = 2 \end{aligned}$ . Use the shell method to compute the volume of the solid.
::将 R 区域旋转到 x 轴周围,从而生成一个固态数字。 R 受曲线 y=x2 和行 x=0 和行 x =2 的约束, 使用 shell 方法计算固体的体积。

Because the volume is generated by rotating around the $\begin{aligned} x \end{aligned}$ -axis, the volume is given by:
::由于该音量是围绕 X 轴旋转产生的,因此该音量由下列单位提供:

$\begin{aligned} V = \int_{c}^{d} 2 π r h d y, \end{aligned}$

::

From the figure, we can identify the limits of integration: $\begin{aligned} y \end{aligned}$ runs from 0 to 4. A horizontal strip of this region would generate a cylinder with height $\begin{aligned} 2 - \sqrt{y} \end{aligned}$ and radius $\begin{aligned} y \end{aligned}$ .
::从图中,我们可以确定整合的限度:y 运行从0到4。该区域的水平条将产生一个高度为2-y和半径为y的圆筒。

Thus the volume of the solid will be
::因此,固体的体积将是

$\begin{aligned} V & = \int_{c}^{d} 2 π r h d y \\ = \int_{0}^{4} 2 π y (2 - \sqrt{y}) d y \\ = 2 π \int_{0}^{4} (2 y - y^{\frac{3}{2}}) d y \\ = 2 π {[y^{2} - \frac{2}{5} y^{\frac{5}{2}}]}_{0}^{4} \\ = \frac{32 π}{5} . \end{aligned}$

::Vcd2rhdy042y(2-y)dy=204(2y-y)y32dy=2[y2-2555]04=325。

The alert reader will have noticed that this example could be worked with a simpler integral using disks.
::提醒阅读器会注意到,这个例子可以用一个使用磁盘的更简便的集成件来操作。

Example 3
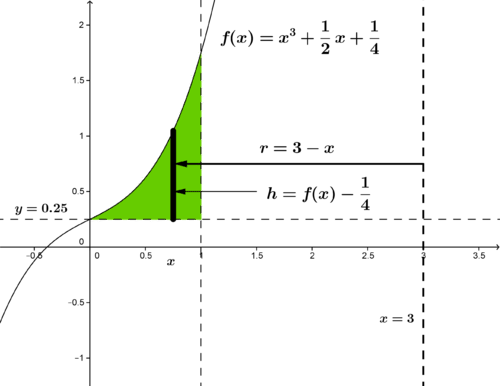
::例3

Find the volume of the solid generated by revolving the region bounded by $\begin{aligned} y = x^{3} + \frac{1}{2} x + \frac{1}{4} \end{aligned}$ , $\begin{aligned} y = \frac{1}{4} \end{aligned}$ and $\begin{aligned} x = 1 \end{aligned}$ about $\begin{aligned} x = 3 \end{aligned}$ .
::查找y=x3+12x+14、y=14和 x=1 约x=3 区域旋转产生的固体体积。

As you can see, the equation $\begin{aligned} y = x^{3} + \frac{1}{2} x + \frac{1}{4} \end{aligned}$ cannot be easily solved for $\begin{aligned} x \end{aligned}$ and therefore it will be necessary to solve the problem by the shell method. We are revolving the region about a line parallel to the $\begin{aligned} y \end{aligned}$ -axis and thus integrate with respect to $\begin{aligned} x \end{aligned}$ Our formula is
::您可以看到, y=x3+12x+14 等公式对于 x 来说不容易解决, 因此有必要用 shell 方法解决问题。我们正在将区域旋转到与 Y 轴平行的一条线上, 从而结合到 x 。我们的公式是

$\begin{aligned} V = \int_{a}^{b} 2 π r h d x . \end{aligned}$
.
::瓦布2rhdx..

In this case, the radius is $\begin{aligned} 3 - x \end{aligned}$ and the height is $\begin{aligned} y - \frac{1}{4} \end{aligned}$ . Substituting,
::在这种情况下,半径为3-x,高度为y-14。

$\begin{aligned} V & = 2 π \int_{0}^{1} (3 - x) (x^{3} + \frac{1}{2} x + \frac{1}{4} - \frac{1}{4}) d x \\ = 2 π \int_{0}^{1} (- x^{4} + 3 x^{3} - \frac{1}{2} x^{2} + \frac{3}{2} x) d x \\ = 2 π {[\frac{- 1}{5} x^{5} + \frac{3}{4} x^{4} - \frac{1}{6} x^{3} + \frac{3}{4} x^{2}]}_{0}^{1} \\ = 2 π [\frac{- 1}{5} + \frac{3}{4} - \frac{1}{6} + \frac{3}{4}] \\ = 2 π [\frac{17}{15}] \\ = \frac{34 π}{15} . \end{aligned}$

::V=201(3-x)(x3+12x+14-14)dx=201(-x4+3x3-12x2+32x)dx=2}[-15x5+34x4-16x3+34x2]01=2}[-15+34-16+34]=2}[1715]=34}15。

Review
::回顾

For #1-10, use cylindrical shells to find the volume generated when the region bounded by the curves is revolved about the axis indicated.
::对于 # 1- 10, 使用圆柱形贝壳来找到曲线所覆盖的区域围绕所示轴旋转时产生的体积。

$\begin{aligned} y = x \end{aligned}$ , $\begin{aligned} y = 0 \end{aligned}$ , $\begin{aligned} x = 2 \end{aligned}$ , about the $\begin{aligned} y \end{aligned}$ -axis
::y=x, y=0, x=2, 有关 Y 轴的 Y 轴

$\begin{aligned} y = x \end{aligned}$ , $\begin{aligned} y = - \frac{x}{2} \end{aligned}$ , $\begin{aligned} x = 2 \end{aligned}$ , about the $\begin{aligned} y \end{aligned}$ -axis
::y=x, yx2, x=2, 有关 Y 轴

$\begin{aligned} y = \sqrt{x} \end{aligned}$ , $\begin{aligned} y = \sqrt{3} \end{aligned}$ , about the $\begin{aligned} y \end{aligned}$ -axis
::y=x,y=3,关于y轴

$\begin{aligned} y = x \end{aligned}$ , $\begin{aligned} y = 0 \end{aligned}$ , $\begin{aligned} x = 2 \end{aligned}$ , about the $\begin{aligned} x \end{aligned}$ -axis
::y=x, y=0, x=2, 关于 x 轴

$\begin{aligned} y = \sqrt{x} \end{aligned}$ , $\begin{aligned} y = \sqrt{3} \end{aligned}$ , about the $\begin{aligned} x \end{aligned}$ -axis
::y=x, y=3, 关于 x 轴

$\begin{aligned} y = \frac{1}{x} \end{aligned}$ , $\begin{aligned} y = 0 \end{aligned}$ , $\begin{aligned} x = 1 \end{aligned}$ , $\begin{aligned} x = 3 \end{aligned}$ , about the $\begin{aligned} y \end{aligned}$ -axis
::y=1x, y=0, x=1, x=3 有关 Y 轴的 Y=1x, y=0, x=1, x=3

$\begin{aligned} y = 2 x - 1 \end{aligned}$ , $\begin{aligned} y = - 2 x + 3 \end{aligned}$ , $\begin{aligned} x = 2 \end{aligned}$ , about the $\begin{aligned} y \end{aligned}$ -axis
::y=2x- 1, y2x+3, x=2, 有关 Y 轴的 Y 轴

$\begin{aligned} y = - \frac{4}{9} (x^{2} - 10 x + 16) \end{aligned}$ , $\begin{aligned} y = 0 \end{aligned}$ , about the $\begin{aligned} y \end{aligned}$ -axis
::y49(x2- 10x+16), y=0 y轴

$\begin{aligned} y = x^{2} \end{aligned}$ , $\begin{aligned} x = 1 \end{aligned}$ , $\begin{aligned} y = 0 \end{aligned}$ , about the $\begin{aligned} x \end{aligned}$ -axis
::y=x2, x=1, y=0 关于 x 轴的 y=2, x=1, Y=0

$\begin{aligned} y^{2} = x \end{aligned}$ , $\begin{aligned} y = 1 \end{aligned}$ , $\begin{aligned} x = 0 \end{aligned}$ , about the $\begin{aligned} x \end{aligned}$ -axis.
::y2=x, y=1, x=0, 关于 x 轴。

Use the cylindrical shells method to find the volume generated when the region is bounded by $\begin{aligned} y = x^{3} \end{aligned}$ , $\begin{aligned} y = 1 \end{aligned}$ , $\begin{aligned} x = 0 \end{aligned}$ is revolved about the line $\begin{aligned} y = 1 \end{aligned}$ .
::使用圆柱形贝壳方法来查找当区域被y=x3、y=1、 x=0 围绕 y=1 线旋转时生成的音量。

Find the volume of the solid generated by rotating the curve $\begin{aligned} y = 3 x + 2 \end{aligned}$ about the $\begin{aligned} x \end{aligned}$ -axis on the interval $\begin{aligned} 0 \leq x \leq 4 \end{aligned}$ using the method of cylindrical shells.
::使用圆柱形外壳的方法,在间距 0 ×x 4 的 X 轴上, 找到旋转 y= 3x+2 所生成的关于 X 轴的固体体积。

Find the volume of the solid generated by rotating about the line $\begin{aligned} x = 4 \end{aligned}$ the area between the curves $\begin{aligned} x = 2 \end{aligned}$ , $\begin{aligned} y = \sqrt{x - 1} \end{aligned}$ and the $\begin{aligned} x \end{aligned}$ -axis, using the method of cylindrical shells.
::使用圆柱形外壳的方法,在 x=4 线上旋转产生的固体体积、曲线 x=2 、 y=x-1 和 x 轴之间的区域,以查找圆柱形外壳所生成的固体体积。

Find the volume of the solid generated by rotating about the line $\begin{aligned} x = - 2 \end{aligned}$ , the region bounded by the curves $\begin{aligned} y = 4 \end{aligned}$ and $\begin{aligned} y = - x^{2} + 4 x + 1 \end{aligned}$ , using the method of cylindrical shells.
::使用圆柱形贝壳的方法,在x2线周围旋转产生的固体体积、以 y=4 和 y2+4x+1 曲线为界的区域,查找圆柱形贝壳周围旋转产生的固体体积。

Set up, but do not solve, an integral to find the volume of the solid generated by rotating about the line $\begin{aligned} x = π \end{aligned}$ the area bounded by the curves $\begin{aligned} x = π \end{aligned}$ , $\begin{aligned} x = \frac{π}{2} \end{aligned}$ and $\begin{aligned} y = \sin (x) \end{aligned}$ , using the method of cylindrical shells.
::设置, 但不解析, 使用圆柱形外壳的方法, 以查找在“ line x ” 周围旋转所生成的固体体积。

Find the volume of the solid generated by rotating about the $\begin{aligned} y - \end{aligned}$ axis the area bounded by the curves $\begin{aligned} y = 13 - x^{2} \end{aligned}$ and $\begin{aligned} y = x^{2} - 8 x + 19 \end{aligned}$ using the method of cylindrical shells.
::使用圆柱形外壳的方法,在 y- 轴上旋转曲线y= 13- x2和y=x2-8x+19所包围的区域,查找圆柱形外壳周围旋转产生的固体体积。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Volumes by Cylindrical Shell ::圆柱形壳壳体积

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)

Volumes by Cylindrical Shell
::圆柱形壳壳体积

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Review
::回顾

Review (Answers)
::回顾(答复)