平板曲线的长度

播放段落

Length of a Plane Curve
::平面曲线的长度

播放段落

In this section will consider the problem of finding the length of a plane curve. Formulas for finding the arcs of circles appeared in early historical records and they were known to many civilizations. However, very little was known about finding the lengths of general curves, such as the length of the curve  $\begin{align*}y=x^{\frac{3}{2}}\end{align*}$ in the interval [1, 3] until the discovery of calculus in the seventeenth century.
::本节将讨论寻找平面曲线长度的问题。早期历史记录中出现了寻找圆圈弧的公式,许多文明都了解这些公式。然而,在找到一般曲线长度方面却鲜为人知,如在17世纪发现微积分之前的间隔[1,3]内曲线 y=x32的长度。

播放段落

In calculus, we define an  arc length as the length of a smooth plane curve  $\begin{align*}y=f(x)\end{align*}$ over an interval $\begin{align*}[a,b]\end{align*}$ . By smooth plane curve we mean if  $\begin{align*}y=f(x)\end{align*}$  has a continuous first derivative, $\begin{align*}f^\prime\end{align*}$ , on $\begin{align*}[a,b]\end{align*}$ , then  $\begin{align*}f\end{align*}$ is said to be a smooth function (or smooth curve) on $\begin{align*}[a,b]\end{align*}$ .
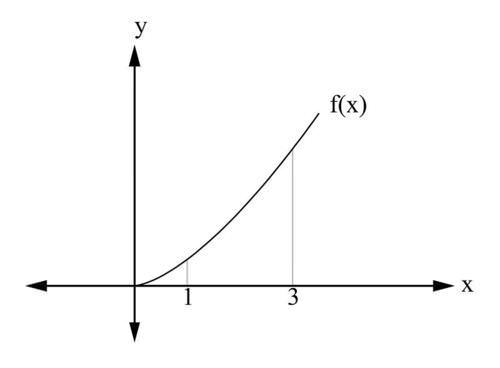
::在微积分中,我们将弧长度定义为平滑平面曲线y=f(x)在间隔[a,b]中的长度。用平滑平面曲线表示,如果y=f(x)在[a,b]上具有连续的第一个衍生物 f',那么,f在[a,b]上被称为平稳函数(或平滑曲线)。

播放段落

An example of a smooth curve  $\begin{align*}y=f(x)\end{align*}$ on  $\begin{align*}[a,b]\end{align*}$ is depicted below.
::下文举例说明了[a,b] 上的平滑曲线y=f(x)的例子。

播放段落

The arc length is defined as if  $\begin{align*}y=f(x)\end{align*}$ is a smooth curve on the interval  $\begin{align*}[a,b]\end{align*}$ then the arc length  $\begin{align*}L\end{align*}$ of this curve is defined as
::弧弧长度被定义为 Y=f(x) 是间距[a,b] 的平滑曲线, 然后这个曲线的弧长度 L 被定义为

播放段落

$$\begin{align*}L=\int\limits_a^b\sqrt{1+[f^\prime (x)]^2}dx=\int\limits_a^b\sqrt{1+ \left(\frac{dy}{dx} \right)^2}dx.\end{align*}$$
::L=ba1+[f_(x)]2dx=ba1+(uddx)2dx。

播放段落

Similarly,
::同样,

播放段落

If  "> $\begin{align*}x=f(y)\end{align*}$ is a smooth curve on the interval  $\begin{align*}[c,d]\end{align*}$ then the arc length $\begin{align*}L\end{align*}$ of this curve is defined as
::如果 x=f 是间距[c,d] 上的平滑曲线,则此曲线的弧长L定义为

播放段落

%5D%5E2%7Ddy%3D%5Cint%5Climits_c%5Ed%5Csqrt%7B1%2B%20%5Cleft(%5Cfrac%7Bdx%7D%7Bdy%7D%20%5Cright)%5E2%7Ddy.">

$$\begin{align*}L=\int\limits_c^d\sqrt{1+[f^\prime (y)]^2}dy=\int\limits_c^d\sqrt{1+ \left(\frac{dx}{dy} \right)^2}dy.\end{align*}$$
::L=dc1+[f]2dy=dc1+(dxdy)2dy。

播放段落

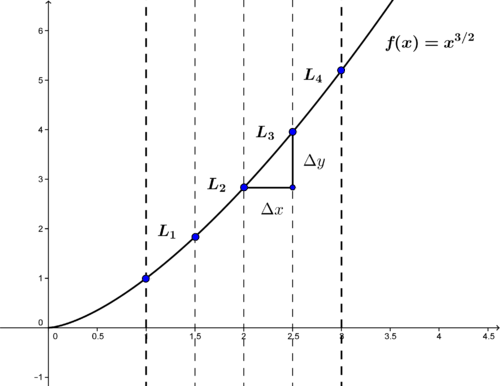
The above definitions come from the recognition that the smooth function curve can be approximated over the interval  $\begin{align*}[a,b]\end{align*}$ by a large number of straight line segments (e.g., see line segment sample, $\begin{align*}L_k\end{align*}$  below) whose length can be computed using the distance formula (Pythagorean theorem); these segments can then be sumed to provide an estimate of the length of the curve. The more line segments, the better the estimate.
::上述定义源于承认平滑函数曲线可以在间距[a,b]中以大量直线段相近(例如,见线段样本,下k),其长度可以用距离公式(Pythagorean定理)计算;然后可以对这些部分进行总和,以提供曲线长度的估计。线段越多,估计越好。

播放段落

The summation of the line segments, $\begin{align*}L_k\end{align*}$  is a of lengths, given by.
::Lk是线段总和的长度,由给定 。

播放段落

$$\begin{align*}L &\approx \sum_{k=1}^n L_k \\ &\approx \sum_{k=1}^n \triangle x \sqrt{1+\left[ \frac{f(x_k+\triangle x)-f(x_k)}{\triangle x} \right]^2} \quad \ldots \text{ Riemann Sums where }\triangle x=\frac{b-a}{n} \\ L&=\lim_{n \to \infty}\left[\sum_{k=1}^n \left(\sqrt{1+ \left[\frac{f(x_k+ \triangle x)-f(x_k)}{\triangle x} \right]^2}\triangle x \right) \right] \\ &=\int\limits_a^b\sqrt{1+[f^\prime (x)]^2}dx \\ L&=\int\limits_a^b\sqrt{1+ \left[\frac{dy}{dx} \right]^2}dx\end{align*}$$
::{{{{{{{{{{{{{{{{{{{{{}}}}1{{{{{{{{{{}}}1{{{{{{{{}}}{{{{{{}}}}}{{{{{{{{{{{{}}}{{{{{{}}}}}{{{{{{{}}}{{{{{{{}}}}}{{{{{{{}}}}}{{{{{{{{{{{}}}}}}}{{{{{{{{{{}}}}}}}}}{{{{{{{{{{}}}}}}}}}{{{{{{{{{{{{{{{}}}}}}{{{{{{{{{}}}}}}}{{{{{{{}}}}}}}}}}}{{{{{{{{{}}}}}}}}}}}}}{{{{{{{{{{{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

播放段落

Apply your knowledge of arc length to find the arc length of the curve  $\begin{align*}y=x^{\frac{3}{2}}\end{align*}$  on [1, 3] by using Riemann sums with $\begin{align*}n=4\end{align*}$ .
::应用您对弧长度的知识在 [1, 3] 上找到曲线 y=x32 的弧长度, 使用 Riemann 和 n=4 的数值 。

播放段落

The interval [1, 3] can be divided into  $\begin{align*}n\end{align*}$ sub-intervals of width $\begin{align*}\triangle x=\frac{b-a}{n}=\frac{2}{n}\end{align*}$ . If we take right endpoints, function values can be expressed as  $\begin{align*}f(x_i)=\left(i \frac{2}{n} \right)^{\frac{3}{2}}\end{align*}$ with  $\begin{align*}i=0\end{align*}$ to $\begin{align*}n\end{align*}$ .
::间距 [1, 3] 可以分为 n 的宽度 {x=b- an=2n 的次间隔。 如果我们选取右端点, 函数值可以用 f( xi) =( i2n) 32 和 i= 0 到 n 表示 。

播放段落

$$\begin{align*}L \approx \sum_{i=1}^n L_i=\sum_{k=1}^n\left[\sqrt{\triangle x_i^2+ \triangle y_i^2}\right]=\sum_{i=1}^n \sqrt{\left(\frac{2}{n} \right)^2+\left(\left[1+i \frac{2}{n} \right]^{\frac{3}{2}}-\left[1+(i-1) \frac{2}{n} \right]^{\frac{3}{2}} \right)^2}\end{align*}$$
::Lni=1Li=1Lik=1[x2iy2i]=ni=1(2n)2+([1+i2n]32-[1+(i-1)2n]2]2

播放段落

The table below shows the estimate of the arc length for $\begin{align*}n=4\end{align*}$ .
::下表显示n=4的弧长度估计数。

播放段落

Now, let’s see what the arc length definite integral yields.
::现在,让我们来看看什么是弧长度 确定的整体产量。

播放段落

Find the arc length of the curve  $\begin{align*}y=x^{\frac{3}{2}}\end{align*}$  on [1, 3].
::在 [1, 3] 上查找曲线 y=x32 的弧长度。

播放段落

Since  $\begin{align*}y=x^{\frac{3}{2}}\end{align*}$ , $\begin{align*}\frac{dy}{dx}=\frac{3}{2} x^{\frac{1}{2}}\end{align*}$ .
::从y=x32, dydx=32x12开始。

播放段落

Using the definite integral form of the arc length formula, we get:
::使用弧长度公式的明确整体形式,我们得到:

播放段落

$$\begin{align*}L&=\int\limits_a^b\sqrt{1+[f^\prime (x)]^2}dx \\ &=\int\limits_1^3\sqrt{1+\left[\frac{3}{2} x^{\frac{1}{2}} \right]^2}dx \\ &=\int\limits_1^3\sqrt{1+ \frac{9}{4}x} \ dx \quad \ldots \text{Uses change of variables (u-substitution) as follows:}\\ &=\int\limits_{\frac{13}{4}}^{\frac{31}{4}} \frac{4}{9} \sqrt{u} \ du \qquad \ u=1+ \frac{9}{4} x \text{ and } du=\frac{9}{4}dx, \text{ and change the integration limits}. \\ &=\frac{4}{9}\left[\frac{2}{3} u^{\frac{3}{2}} \right]_{\frac{13}{4}}^{\frac{31}{4}} \\ &\approx 4.66\end{align*}$$
::L=baa1+[f}(x)]2dx=3111+[32x12]2dx=311+94xdx...使用变数变化(u-替代)如下:=31413449u u=1+94x和du=94dx,并更改整合限制。=49[23u32]3141344.66。

播放段落

The length of the arc of $\begin{align*}y=x^{\frac{3}{2}}\end{align*}$  on the interval [1, 3] is $\begin{align*}\approx 4.66\end{align*}$ .
::间隔 [1, 3] 的 y=x32 弧的长度为 4. 66。

播放段落

How would the arc length determination be made if the integration were made along the $\begin{align*}y\end{align*}$ -axis instead of the $\begin{align*}x\end{align*}$ -axis. Would we get the same arc length value?
::如果按照 y 轴而不是 x 轴来进行整合, 则如何确定弧长度 。 我们是否能得到相同的弧长度值 ?

播放段落

Find the arc length of the curve  $\begin{align*}y=x^{\frac{3}{2}}\end{align*}$  on [1, 3], but using integration along the $\begin{align*}y\end{align*}$ -axis.
::在 [1, 3] 上查找曲线 y=x32 的弧长度,但使用 Y 轴的集成。

播放段落

Since  $\begin{align*}y=x^{\frac{3}{2}}\end{align*}$ , solving for  $\begin{align*}x\end{align*}$ gives the inverse relationship %3Dy%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D"> $\begin{align*}x=f(y)=y^{\frac{2}{3}}\end{align*}$ , and  $\begin{align*}\frac{dx}{dy}=\frac{2}{3} y^{\frac{-1}{3}}\end{align*}$ .
::由于 y=x32, 解析 x 时会给出反向关系 x=f =y23 和 dxdy= 23y- 13 。

播放段落

Using the arc length formula  %5D%5E2%7D%20dy%3D%5Cint%5Climits_c%5Ed%20%5Csqrt%7B1%2B%20%5Cleft(%5Cfrac%7Bdx%7D%7Bdy%7D%20%5Cright)%5E2%7Ddy"> $\begin{align*}L=\int\limits_c^d \sqrt{1+[f^\prime (y)]^2} dy=\int\limits_c^d \sqrt{1+ \left(\frac{dx}{dy} \right)^2}dy\end{align*}$ above, we get:
::使用上文弧长度公式L=dc1+[f]2dy=dc1+(dxdy)2dy,我们得到:

播放段落

%5D%5E2%7D%20dy%20%5C%5C%0A%26%3D%5Cint%5Climits_1%5E%7B3%5Csqrt%7B3%7D%7D%5Csqrt%7B1%2B%5Cleft%5B%5Cfrac%7B2%7D%7B3%7Dy%5E%7B%5Cfrac%7B-1%7D%7B3%7D%7D%20%5Cright%5D%5E2%7D%20dy%20%26%26%20%5Cldots%20%5Ctext%7BWhere%7D%20%5C%20c%20%5C%20%5Ctext%7Band%7D%20%5C%20d%20%5C%20%5Ctext%7Bare%20determined%20from%7D%20%5C%20x%3D1%20%5C%20%5Ctext%7Band%7D%20%5C%20x%3D3%20%5C%5C%0A%26%3D%5Cint%5Climits_1%5E%7B3%5Csqrt%7B3%7D%7D%5Csqrt%7B1%2B%20%5Cfrac%7B4%7D%7B9%7D%20y%5E%7B%5Cfrac%7B-2%7D%7B3%7D%7D%7Ddy%20%26%26%20%5Cqquad%20%5Ctext%7Brespectively%3A%7D%20%5C%20c%3D(1)%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D%3D1%20%5C%20%5Ctext%7Band%7D%20%5C%20d%3D(3)%5E%7B%5Cfrac%7B3%7D%7B2%7D%7D%3D3%5Csqrt%7B3%7D.%20%5C%5C%0AL%26%3D4.66%20%26%26%20%5Cldots%20%5Ctext%7BThe%20integral%20has%20been%20evaluated%20numerically%20using%20a%20calculator%7D.">

$$\begin{align*}L&=\int\limits_c^d \sqrt{1+[f^\prime(y)]^2} dy \\ &=\int\limits_1^{3\sqrt{3}}\sqrt{1+\left[\frac{2}{3}y^{\frac{-1}{3}} \right]^2} dy && \ldots \text{Where} \ c \ \text{and} \ d \ \text{are determined from} \ x=1 \ \text{and} \ x=3 \\ &=\int\limits_1^{3\sqrt{3}}\sqrt{1+ \frac{4}{9} y^{\frac{-2}{3}}}dy && \qquad \text{respectively:} \ c=(1)^{\frac{2}{3}}=1 \ \text{and} \ d=(3)^{\frac{3}{2}}=3\sqrt{3}. \\ L&=4.66 && \ldots \text{The integral has been evaluated numerically using a calculator}.\end{align*}$$
::L=dc1+[f]2dy=33311+[23y-13]2dy...在 x=1 和 x=3=3=33311+49y-23 分别确定为 c=(1)23=1 和 d=(3)32=33.L=4.66的 c和 d=(3)32=33.L=4.66的情况下. 集成体用计算法进行了数字评价。

播放段落

This is the same arc length result from  the problem above. 
::以上问题造成的长度相同。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked if the distance formula can be used to find the length of a curve over some interval. If you postulated that th is is true,  you were correct. If any function curve is divided into enough straight line segments over the interval, the sum of the lengths of the segments gets closer to the length of the function curve. In the limit, the sum goes to the actual value of the curve length, and the sum is represented by a definite integral.
::早些时候,有人问您是否使用距离公式来找到某个间距的曲线长度。 如果您假设这是对的, 您是对的。 如果任何函数曲线在间隔内被分为足够的直线段, 则各段长度的总和会接近函数曲线的长度。 在极限内, 数值会达到曲线长度的实际值, 并且总和会由一个明确的整体表示 。

播放段落

Example 2
::例2

播放段落

Do the functions $\begin{align*}f(x)=\sin \ x\end{align*}$  and $\begin{align*}g(x)=\sin^2 x\end{align*}$  have the same arc length in the interval  $\begin{align*}[0, \ 2 \pi]\end{align*}$ ?
::函数 f( x) =sin x 和 g( x) =sin2x 在间隔 [0, 2] 中是否有相同的弧长度 ?

播放段落

To answer the question requires evaluation of the arc lengths of both functions over the interval. The evaluation is as follows:
::要回答问题,就必须在间隔期间对两个职能的弧长度进行评价。

播放段落

In both cases, the integral is evaluated numerically using a calculator. Both results are found to be the same to two decimal places.
::在这两种情况下,综合体都使用计算器进行数字评价,结果与小数点后两位数相同。

播放段落

Review
::回顾

播放段落
1. Are all polynomials smooth functions?
   ::所有多边性功能均平稳吗 ?
播放段落
2. Let  $\begin{align*}f(x)\end{align*}$ equal  $\begin{align*}x\end{align*}$ for all $\begin{align*}x > 0\end{align*}$ , and equal zero otherwise. Is this a smooth function?
   ::Letf(x) 等於 x 全部 x>0 的 x, 否则等于 0。 这是平滑的函数吗 ?
播放段落
3. Are all linear combinations of smooth functions also smooth functions?
   ::平滑函数的所有线性组合是否也平滑功能?
播放段落
4. Is the function  $\begin{align*}f(x)=x^2 \tan(x)\end{align*}$ smooth?
   ::函数 f( x) =x2tan( x) 平滑吗 ?
播放段落
5. Find the arc length of the curve  $\begin{align*}y=\frac{(x^2+2)^{\frac{3}{2}}}{3}\end{align*}$ on [0, 3].
   ::在 [0, 3] 上查找曲线y=(x2+2)323的弧长度。
播放段落
6. Find the arc length of the curve  $\begin{align*}x=\frac{1}{6} y^3+ \frac{1}{2y}\end{align*}$ on $\begin{align*}y \in [1, \ 2]\end{align*}$ .
   ::在 y[1, 2] 上查找曲线 x=16y3+12y 的弧长度。
播放段落
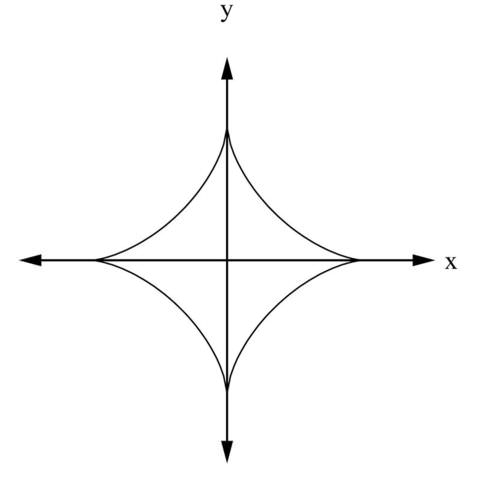
7. Find the length of the curve shown in the figure below. The shape of the graph is called the astroid because it looks like a star. The equation of its graph is $\begin{align*}x^{\frac{2}{3}}+y^{\frac{2}{3}}=1\end{align*}$ .
   ::查找下图中显示的曲线长度。 图形的形状被称为小行星, 因为它看起来像一颗恒星。 图形的方程式是 x23+y23=1 。

播放段落
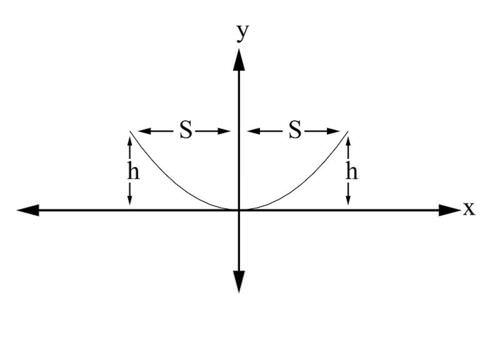
9. The figure below shows a suspension bridge. The cable has the shape of a parabola with equation $\begin{align*}x^2=y\end{align*}$ . The suspension bridge has a total length of  $\begin{align*}2S\end{align*}$ and the height of the cable is  $\begin{align*}h\end{align*}$ at each end. Show that the total length of the cable is $\begin{align*}L=2 \int\limits_0^s \sqrt{1+\frac{4h^2}{S^4}x^2} dx\end{align*}$ .
   ::下图显示悬浮桥。 电缆的形状是具有等式x2=y的抛光线。 悬浮桥的总长度为2S, 电缆的高度为每端 h。 显示电缆的总长度为 L=2s01+4h2S4x2dx。

播放段落
10. Use the arc length formula to verify that the length of the curve $\begin{align*}x=c\end{align*}$ , where  $\begin{align*}c\end{align*}$ is a constant, is 1 between the points  $\begin{align*}x=0\end{align*}$ and $\begin{align*}x=1\end{align*}$ .
    ::使用弧长度公式来验证曲线x=c(其中 c 是常数)的长度是 x=0 和 x=1 之间的1。
播放段落
11. Set up, but do not evaluate, the integral used to evaluate the length of  $\begin{align*}\ln(x^2+ \sin(x))\end{align*}$ between [15, 25].
    ::设置但不评价用于评价 In(x2+sin(x))在 [15、25] 之间的长度的集成件。
播放段落
12. What is the length of  $\begin{align*}\frac{2}{3}(x-1)^{\frac{3}{2}}\end{align*}$ between [0, 5] ?
    ::[0,5]之间23(x-1)32之间的长度是多少?
播放段落
13. Set up, but do not evaluate, the integral used to evaluate the length of  $\begin{align*}2x^3+4x^2-x-1\end{align*}$ between [1, 3].
    ::设置但不评价用于评价[1、3]之间2x3+4x2-x-1长度的集成件。
播放段落
14. Set up, but do not evaluate, the integral used to evaluate the length of  $\begin{align*}x=y+y^3\end{align*}$ between [1, 4].
    ::设置用于评价 x=y+y3 在 [1, 4] 之间的长度的内装件, 但不进行评价 。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。