节: 参数形式和微积分:平面面积 | 10.6 参数形式和微积分:平面面积

章节大纲

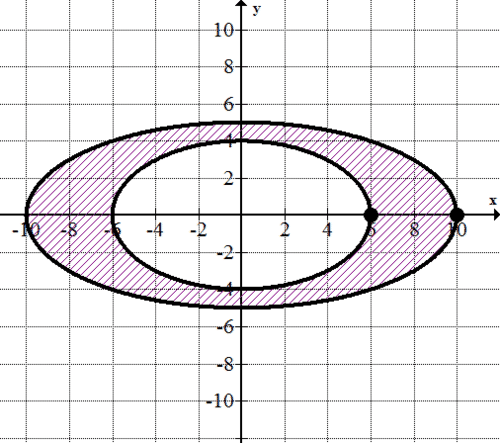
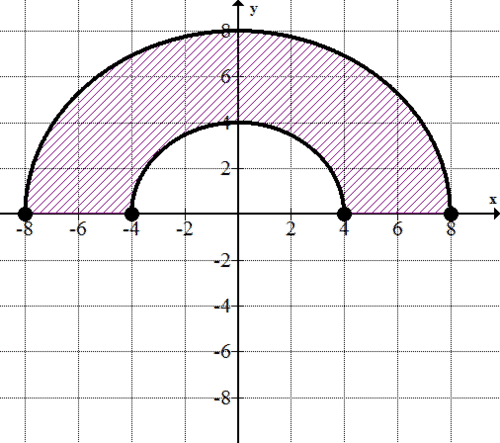
The Springdale Community Park District is applying for a grant so that the town can install a new, rubber running track. The grant writers need to know the area of the running surface so that they can predict the cost of the new track. A runner’s path along the outermost edge of the track can be described by the parametric equation
::斯普林代尔社区公园区正在申请一笔赠款,以便该镇能够安装一个新的橡胶运行轨迹。赠款作者需要了解运行的表面面积,以便他们能够预测新轨迹的成本。赛跑者沿赛道外围的路径可以用参数方程描述。

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 10 \cos t \\ y (t) & = 5 \sin t \end{aligned}$

::F(t) = (x(t) y(t) ) x(t) = 10costy(t) = 5sint

While a walker’s path along the innermost edge can be described as
::步行者沿着最深边缘的道路可以说是:

$\begin{aligned} G (t) & = (x (t), y (t)) \\ x (t) & = 6 \cos t \\ y (t) & = 4 \sin t \end{aligned}$

::G( t) = (x( t) y( t) ) x( t) = 6costy( t) = 4sint

All measurements are in terms of minutes and meters. How many square meters of rubber surface will the park district need to purchase in order to create these new tracks?
::公园区需要购买多少平方米的橡胶表面才能建立这些新轨道?

Area Under a Parametric Curve
::参数曲线下的区域

To find the area under a parametric curve, you’ll need to integrate. A simple tool allows you to integrate in terms of $\begin{aligned} t \end{aligned}$ . A typical integral takes the form $\begin{aligned} \int_{a}^{b} f (x) d x \end{aligned}$ . To integrate a parametric equation, multiply the quantity under the integral by $\begin{aligned} \frac{d t}{d t} \end{aligned}$ . This is just a form of the number 1, but it lets you rewrite the integral as:
::要在参数曲线下找到区域, 您需要整合。一个简单的工具允许您以 t 的方式整合区域。一个典型的集成以 {abf( x) dx 的形式整合。要整合参数方程式, 请将集成下的数量乘以 dtdt 。这只是数字 1 的一种形式, 但它允许您将集成内容重写为 : @ abf( x) dx 。

$\begin{aligned} \int_{t_{0}}^{t_{1}} f (x) d x \frac{d t}{d t} = \int_{t_{0}}^{t_{1}} f (t) \frac{d x}{d t} d t \end{aligned}$

::{t0t1f(x) dxdtdt}}t0t1f(t) dddtt} (x) dddddt}(x) ddddt}t0t0t1f(t) ddddtt

Now, $\begin{aligned} f (t) \end{aligned}$ is the same as $\begin{aligned} y (t) \end{aligned}$ , and $\begin{aligned} \frac{d x}{d t} = x^{'} (t) \end{aligned}$ . This means that you can rewrite the integral as the product of $\begin{aligned} y (t) \end{aligned}$ and $\begin{aligned} x^{'} (t) \end{aligned}$ ,
::f( t) 与 y( t) 相同, dxdt=x_x_( t) 相同。这意味着您可以重写 y( t) 和 x_( t) 的产物为 y( t) 和 x_( t) ,

$\begin{aligned} \int_{t_{0}}^{t_{1}} f (t) \frac{d x}{d t} d t = \int_{t_{0}}^{t_{1}} y (t) x^{'} (t) d t \end{aligned}$

::t0t1f( t) dddtdtt0t1y( t)x_( t) dt

and then evaluate.
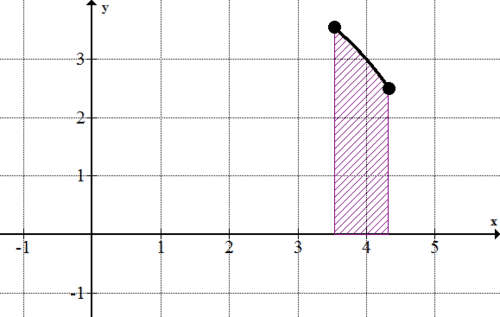
::然后进行评估。

Let's find the defined by the following function between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = 10 \end{aligned}$ .
::让我们在 t=0 和 t=10 之间找到以下函数定义的函数。

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 2 t \\ y (t) & = 3 t + 4 t^{2} \end{aligned}$

::F(t) = (x(t) y(t) ) x(t) = 2ty(t) = 3t+4t2

First, start with the form for a parametric integral, then solve:
::首先,先从参数元件的表单开始,然后解答:

$\begin{aligned} A & = \int_{0}^{10} y (t) x^{'} (t) d t \\ x (t) & = 2 t \\ x^{'} (t) & = 2 \\ y (t) & = 3 t + 4 t^{2} \end{aligned}$

::A010y(t)x_(t)dtx(t)=2tx_(t)=2y(t)=3t+4t2

$\begin{aligned} A & = \int_{0}^{10} (3 t + 4 t^{2}) (2) d t \\ = 2 \int_{0}^{10} (3 t + 4 t^{2}) d t \\ = 2 {[\frac{3}{2} t^{2} + \frac{4}{3} t^{3}]}_{0}^{10} \\ = 2 [(\frac{3 (100)}{2} + \frac{4 (1000)}{3}) - 0] \\ = 2 [\frac{8900}{6}] \\ = 1483 \frac{1}{3} \end{aligned}$

::A010(3t+4t2)(2)dt=2010(3t+4t2)dt=2[32t2+43t3]010=2[(3)(1002)+4(1003)-0]=2[89006]=148313

The area under the curve is $\begin{aligned} 1483 \frac{1}{3} \end{aligned}$ units squared. This area is shown shaded below:
::曲线下的区域为148313 单位平方。此区域显示在下面的阴影下:

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine how many square meters of rubber surface a park district will need to purchase in order to build a running track. The path of the outermost edge is described by:
::先前曾要求你确定公园区需要购买多少平方米的橡胶表面才能建立运行轨迹。

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 10 \cos t \\ y (t) & = 5 \sin t \end{aligned}$

::F(t) = (x(t) y(t) ) x(t) = 10costy(t) = 5sint

The path of the inner most edge is described by :
::内部最边缘的路径描述如下:

$\begin{aligned} G (t) & = (x (t), y (t)) \\ x (t) & = 6 \cos t \\ y (t) & = 4 \sin t \end{aligned}$

::G( t) = (x( t) y( t) ) x( t) = 6costy( t) = 4sint

The curves are symmetrical across the $\begin{aligned} x \end{aligned}$ -axis, so you can find the area of the top half of each and then double it. Also, recall that $\begin{aligned} t \end{aligned}$ traverses the curves in a counter-clockwise direction.
::X 轴的曲线对称, 所以您可以找到每个轴的顶部半部区域, 然后翻一番。另外, 提醒您注意, 曲线在逆时针方向穿行。

$F(t)$ , which defines the outer limit of the track. First, find the area of the ellipse enclosed by the function
::,它定义了轨道的外部界限。首先,找到函数附加的椭圆区域

$& F(t) = (x(t), y(t)) \\& x(t)= 10 \cos t \\& x^{\prime}(t)= -10 \sin(t) \\& y(t) = 5 \sin t$

$\begin{aligned} \int_{0}^{π} y (t) x^{'} (t) d t \\ \int_{0}^{π} 5 \sin (t) (- 10 \sin (t)) d t \\ - 50 \int_{0}^{π} \sin^{2} (t) d t \\ = - 50 {[\frac{1}{2} t - \frac{1}{4} \sin (2 t)]}_{0}^{π} \\ = - 50 [\frac{π}{2} - 0] \\ = - 25 π \end{aligned}$

::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

So, the total area enclosed by the outer edge of the track is $\begin{aligned} 50 π \end{aligned}$ .
::因此,铁轨外缘所封闭的总面积是50英寸。

Now, find the area enclosed by the inner ring of the track.
::现在,找到铁轨内环所包围的区域

$\begin{aligned} G (t) = (x (t), y (t)) \\ x (t) = 6 \cos t \\ x^{'} (t) = - 6 \sin (t) \\ y (t) = 4 \sin t \end{aligned}$

::G( t) = (x( t) y( t) x( t) = 6cos @ tx}( t) @ 6sin( t) y( t) = 4sin}t

$\begin{aligned} \int_{0}^{π} y (t) x^{'} (t) d t \\ \int_{0}^{π} 6 \sin (t) (- 4 \sin (t)) d t \\ = - 24 \int_{0}^{π} \sin^{2} (t) d t \\ = - 24 {[\frac{1}{2} t - \frac{1}{4} \sin (2 t)]}_{0}^{π} \\ = - 24 [\frac{π}{2} - 0] \\ = - 12 π \end{aligned}$

::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

So, the total area enclosed by $\begin{aligned} G (t) \end{aligned}$ (the walker's path) is $\begin{aligned} 24 π \end{aligned}$ . This means that the park district will need $\begin{aligned} 50 π - 24 π = 26 π m^{2} \end{aligned}$ of rubber to cover the track.
::因此,G(t)(行尸路径)所覆盖的总面积是24英寸。这意味着公园区需要502426英寸平方米的橡胶来覆盖铁轨。

Example 2
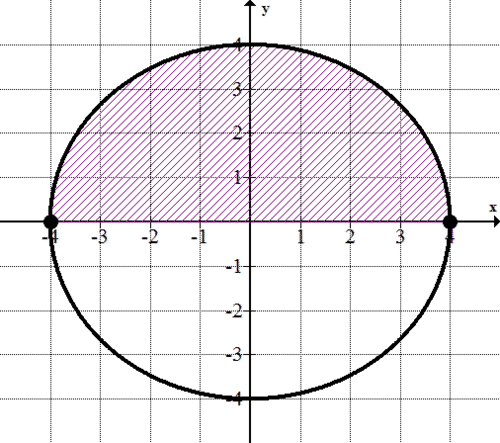
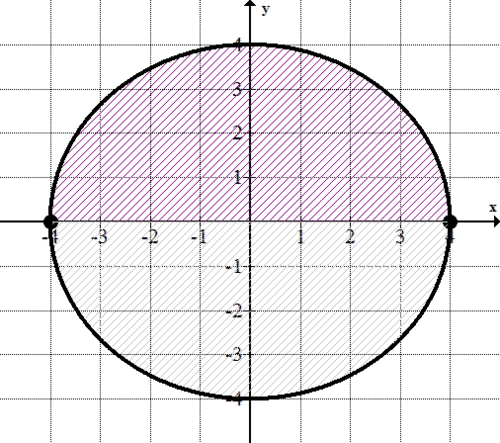
::例2

Use integration to find the area of a circle with a center at (0, 0) described by the following parametric equation:
::使用下列参数方程来查找圆圆区域,圆的中心值为0,0):

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 4 \cos t \\ y (t) & = 4 \sin t \end{aligned}$

::F( t) = (x( t) y( t) ) x( t) = 4costy( t) = 4sint

Since the circle is symmetrical with respect to the $\begin{aligned} x \end{aligned}$ -axis, you can find the area of the top half of the circle (shaded below) and then double it to find the area of the bottom half.
::由于相对于 X 轴的圆对称,您可以找到圆顶半部的区域(下面有阴影),然后翻一番才能找到底部半部的区域。

Start by setting up the integral. Then, integrate using your knowledge of trigonometric functions. Remember that as $\begin{aligned} t \end{aligned}$ traces the complete circle as it moves from 0 to $\begin{aligned} 2 π \end{aligned}$ , you can find the area of the top half of the circle by evaluating the integral from 0 to $\begin{aligned} π \end{aligned}$ . Since $\begin{aligned} t \end{aligned}$ goes from 0 to $\begin{aligned} 2 π \end{aligned}$ , you traverse the circle in a counterclockwise manner. This means that you’ll be integrating ‘backwards’ as $\begin{aligned} t \end{aligned}$ goes from 0 to $\begin{aligned} π \end{aligned}$ .
::以设置集成件开始。然后, 使用您对三角函数的知识集成。记住, 当整个圆从 0 向 2° 移动时, 您可以通过对圆顶半部从 0 到 ° 来评估圆顶部的面积。自 t 从 0 到 2 ° 之后, 您会逆时针绕过圆。这意味着您会像 0 到 ° 那样将“ 向后” 整合。

$\begin{aligned} \int_{0}^{π} y (t) x^{'} (t) d t \\ x (t) = 4 \cos (t) \\ x^{'} (t) = - 4 \sin (t) \end{aligned}$

::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

$\begin{aligned} \int_{0}^{π} 4 \sin t (- 4 \sin (t)) d t \\ = \int_{0}^{π} - 16 \sin^{2} (t) d t \\ = - 16 \int_{0}^{π} \sin^{2} (t) d t \\ = - 16 {[\frac{1}{2} t - \frac{1}{4} \sin (2 t)]}_{0}^{π} \\ = - 16 ([\frac{1}{2} π - \frac{1}{4} \sin (2 π)] - [\frac{1}{2} (0) - \frac{1}{4} \sin (0)]) \\ = - 16 [\frac{π}{2} - 0] \\ = - 8 π \end{aligned}$

::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Why is the area above the $\begin{aligned} x \end{aligned}$ -axis $\begin{aligned} - 8 π \end{aligned}$ ? Because $\begin{aligned} t \end{aligned}$ traverses the circle in a counter clockwise motion. So if you'd been integrating clockwise, the answer would have been $\begin{aligned} 8 π \end{aligned}$ . So the area for half of the circle is $\begin{aligned} 8 π \end{aligned}$ , which means that the area for the whole circle is $\begin{aligned} 16 π \end{aligned}$ .
::为什么在 X 轴 - 8 上方的区域是 ? 因为圆在逆时针运动中横跨圆圈。所以如果你将时钟组合在一起, 答案应该是 8 。所以圆的半个区域是 8 。这意味着整个圆圈的面积是 16 。

Notice that this is the exact same area you would have obtained if you’d used the formula for the area of a circle, where $\begin{aligned} A = π r^{2} \end{aligned}$ .
::请注意,如果您使用Ar2圆区域公式,此区域与您本来可以得到的区域完全相同。

Example 3
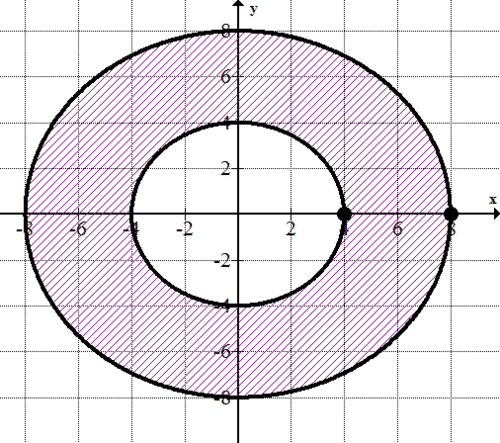
::例3

The area enclosed by the rim of a wheel can be described by the parametric equation:
::轮子边缘封闭的区域可以用参数方程描述:

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 8 \cos t \\ y (t) & = 8 \sin t \end{aligned}$

::F( t) = (x( t) y( t) ) x( t) = 8costy( t) = 8sint

Meanwhile, the area enclosed by the hub of the wheel can be described as:
::同时,车轮枢纽所包围的地区可描述为:

$\begin{aligned} G (t) & = (x (t), y (t)) \\ x (t) & = 4 \cos t \\ y (t) & = 4 \sin t \end{aligned}$

::G(t) = (x(t),y(t)) x(t) = 4costy(t) = 4sint

What is the area of the space between the rim and the hub of the wheel?
::轮子与轮子枢纽之间的空间范围是什么?

To solve this problem, you’ll need to find the area of the circle enclosed by the rim, and then subtract the area of the circle enclosed by the hub.
::为了解决这个问题,您需要找到圆圈的边缘区域,然后减去中枢的圆圈区域。

The remaining area will be the space between the rim and the hub, as shown below.
::如下文所示,其余面积将是边缘与枢纽之间的空间。

First, integrate to find the area enclosed by the rim. Remember that since the circle is symmetrical, you can find the area of the semicircle:
::首先, 集成以找到圆圈所包围的区域。记住, 由于圆圈是对称的, 您可以找到半圆圈的区域 :

Then, you will double that answer to find the total area.
::然后,你会把答案翻倍找到整个区域。

Remember that to find the area of the shaded portion, you will find the area of the circle enclosed by the rim, and then subtract the area of the circle enclosed by the hub. First find the area of the circle enclosed by the rim:
::记住要找到阴暗部分的区域,您可以找到圆圈所包围的圆圈区域,然后减去中枢所包围的圆圈区域。首先,您可以找到圆圈所包围的圆圈区域:

$\begin{aligned} \int_{0}^{π} y (t) x^{'} (t) d t \\ x (t) = 8 \cos (t) \\ x^{'} (t) = - 8 \sin (t) \end{aligned}$

::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

$\begin{aligned} \int_{0}^{π} 8 \sin (t) (- 8 \sin (t)) d t \\ = - 64 \int_{0}^{π} \sin^{2} (t) d t \\ = - 64 {[\frac{1}{2} t - \frac{1}{4} \sin 2 t]}_{0}^{π} \\ = - 64 [[\frac{π}{2} - \frac{1}{4} \sin 2 π] - [\frac{1}{2} (0) - \frac{1}{4} \sin (0)]] \\ = - 32 π \end{aligned}$

::08sin(t)(-8sin(t))dt640sin2(t)dt64[12t-14sin2}064[12t-14sin2}[[2-14sin2]-[12(0)-14sin0]]}32

So, the upper area enclosed by the rim is $\begin{aligned} 32 π \end{aligned}$ .
::因此,上方的边缘地带是32英寸。

Now, use the same process to find the area enclosed by the hub.
::现在,使用同样的程序来找到中心所在区域。

$\begin{aligned} \int_{0}^{π} y (t) x^{'} (t) d t \\ x (t) = 4 \cos t \\ x^{'} (t) = - 4 \sin t \end{aligned}$

::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

$\begin{aligned} \int_{0}^{π} 4 \sin t (- 4 \cos t) d t \\ = - 16 \int_{0}^{π} \sin^{2} (t) d t \\ = - 16 {[\frac{1}{2} t - \frac{1}{4} \sin (2 t)]}_{0}^{π} \\ = - 16 ([\frac{1}{2} (π) - \frac{1}{4} \sin (2 π)] - [\frac{1}{2} (0) - \frac{1}{4} \sin (0)]) \\ = - 8 π \end{aligned}$

::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

So, the upper area of the hub is $\begin{aligned} 8 π \end{aligned}$ . Subtract the hub from the area enclosed by the rim, and you'll see that the upper area between the rim and the hub is $\begin{aligned} 24 π {units}^{2} \end{aligned}$ . This means that the total area between the rim and the hub is $\begin{aligned} 48 π {units}^{2} \end{aligned}$ .
::因此, 中枢的上层面积是 8°。将中枢从边缘封闭的区域中减去, 你会看到中枢和中枢之间的上层面积是 24° 单位 2 。这意味着中枢和中枢之间的总面积是 48° 2 单位 2 。

Example 4
::例4

Find the area under the following curve between $\begin{aligned} t = \frac{π}{6} \end{aligned}$ and $\begin{aligned} t = \frac{π}{4} \end{aligned}$ .
::在t6和t4之间的以下曲线下查找区域。

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 5 \cos (t) \\ y (t) & = 5 \sin (t) \end{aligned}$

::F(t) = (x(t) y(t) ) x(t) = 5cos(t) y(t) = 5sin(t)

To find the area under the curve between $\begin{aligned} \frac{π}{6} \end{aligned}$ and $\begin{aligned} \frac{π}{4} \end{aligned}$ , first use the method for taking the integral of a parametric function, then evaluate.
::要在 6 和 4 之间的曲线下找到区域,先使用参数函数的集成法,然后进行评估。

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 5 \cos (t) \\ y (t) & = 5 \sin (t) \\ x^{'} (t) & = - 5 \sin t \end{aligned}$

::F( t) = (x( t) ,y( t) ) x( t) = 5cos *( t) y( t) = 5sin ( t) x_( t) 5sin}t

$& \int\limits_\frac{\pi}{6}^\frac{\pi}{4} y(t)x^{\prime}(t)dt \\& \int\limits_\frac{\pi}{6}^\frac{\pi}{4} 5 \sin(t) (-5 \sin(t))dt \\&= -25 \int\limits_\frac{\pi}{6}^\frac{\pi}{4} \sin^2(t)dt \\&= -25 \left[\frac{1}{2}t - \frac{1}{4}\sin(2t)\right]_{\frac{\pi}{6}}^{\frac{\pi}{4}} \\&= -25 \left[\left[\frac{\pi}{4}\left(\frac{1}{2}\right) - \frac{1}{4}\sin \frac{\pi}{2}\right] - \left[\frac{1}{2} \left(\frac{\pi}{6}\right) - \frac{1}{4}\sin \frac{\pi}{3}\right]\right] \\&= -25 \left[\left[\frac{\pi - 2}{8}\right] - \left[\frac{\pi}{12} - \frac{\sqrt{3}}{8}\right]\right] \\&= -2.4352$

Since $\begin{aligned} t \end{aligned}$ traverses the circle in a counter-clockwise direction, the area is 2.4352.
::由于圆向反时针方向跨过圆圈,面积为2.4352。

Example 5
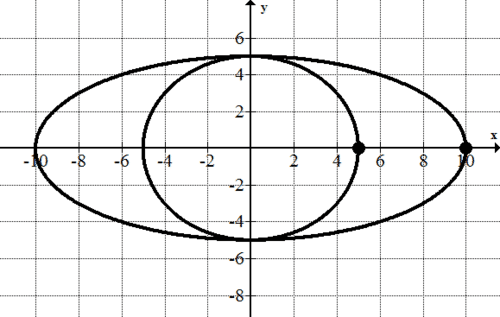
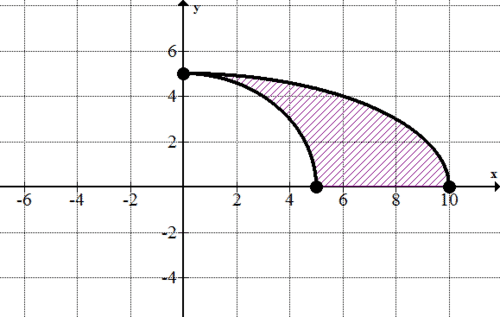
::例5

Find the area between $\begin{aligned} F (t) \end{aligned}$ and $\begin{aligned} G (t) \end{aligned}$ between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = \frac{π}{2} \end{aligned}$ when
::查找 F( t) 和 G( t) 之间在 t= 0 和 t% 2 之间的区域

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 10 \cos (t) \\ y (t) & = 5 \sin (t) \\ G (t) & = (x (t), y (t)) \\ x (t) & = 5 \cos (t) \\ y (t) & = 5 \sin (t) \end{aligned}$

::F( t) = (x( t) ,y( t) ) x( t) = 10cos( t) y( t) = 5sin( t) G( t) = (x( t) ,y( t) x( t) x( t) = 5cos *( t) y( t) y( t) = 5sin( t)

You may want to sketch the curves so that you can see that $\begin{aligned} G (t) \end{aligned}$ is a circle inscribed within the ellipse $\begin{aligned} F (t) \end{aligned}$ .
::您可能想要绘制曲线的草图, 以便您可以看到 G( t) 是一个在椭圆 F( t) 中标定的圆。

Here is the portion between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = \frac{π}{2} \end{aligned}$ , which shaded area that you are looking for:
::这里是 t=0 和 t2 之间的部分, 您正在寻找的阴影区域 :

To find the area, first find the area under $\begin{aligned} F (t) \end{aligned}$ , then subtract the area under $\begin{aligned} G (t) \end{aligned}$ .
::要找到区域,首先在F(t)下找到区域,然后减去G(t)下的区域。

$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 10 \cos (t) \\ x^{'} (t) & = - 10 \sin (t) \\ y (t) & = 5 \sin (t) \end{aligned}$

::F( t) = (x( t) ,y( t) ) x( t) = 10cos @ (t) x_( t) @ 10sin( t) y( t) = 5sin}( t)

$\begin{aligned} \int_{0}^{\frac{π}{2}} y (t) x^{'} (t) d t \\ \int_{0}^{\frac{π}{2}} 5 \sin (t) (- 10 \sin (t)) d t \\ = - 50 \int_{0}^{\frac{π}{2}} \sin^{2} (t) d t \\ = - 50 {[\frac{1}{2} t - \frac{1}{4} \sin (2 t)]}_{0}^{\frac{π}{2}} \\ = - 50 (\frac{π}{4}) \\ = - \frac{25 π}{2} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080} {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

The area under $\begin{aligned} F (t) \end{aligned}$ is $\begin{aligned} \frac{25 π}{2} \end{aligned}$ . Now find the area under $\begin{aligned} G (t) \end{aligned}$ .
::F(t)下的面积为25°2,现在找到G(t)下的面积。

$\begin{aligned} G (t) & = (x (t), y (t)) \\ x (t) & = 5 \cos (t) \\ y (t) & = 5 \sin (t) \end{aligned}$

::G(t) = (x(t) y(t) ) x(t) = 5cos(t) y(t) = 5sin(t)

$\begin{aligned} \int_{0}^{\frac{π}{2}} y (t) x^{'} (t) d t \\ = \int_{0}^{\frac{π}{2}} 5 \sin (t) (- 5 \sin (t)) d t \\ = - 25 \int_{0}^{\frac{π}{2}} \sin^{2} (t) d t \\ = - 25 {[\frac{1}{2} t - \frac{1}{4} \sin (2 t)]}_{0}^{\frac{π}{2}} \\ = - \frac{12.5 π}{2} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

The area under $\begin{aligned} G (t) \end{aligned}$ is $\begin{aligned} \frac{12.5 π}{2} \end{aligned}$ .
::G(t)下的面积为12.5°2。

Now, subtract to find the area between the curves :
::现在, 减去以找到曲线之间的区域 :

$\begin{aligned} \frac{25 π}{2} - \frac{12.5 π}{2} = \frac{12.5 π}{2} \end{aligned}$

The area between the curves is $\begin{aligned} \frac{12.5 π}{2} \end{aligned}$ .
::曲线之间的区域为12.5°2。

Review
::回顾

Find the area under the curve defined below between $\begin{aligned} t = 1 \end{aligned}$ and $\begin{aligned} t = 5 \end{aligned}$ .
$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 4 t^{2} + 6 \\ y (t) & = 8 t \end{aligned}$

::查找以下t=1和t=5.F(t)=(x(t),y(t))x(t)=4t2+6y(t)=8t之间的曲线下区域

Find the area under the curve defined below between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = 10 \end{aligned}$ .
$\begin{aligned} G (t) & = (x (t), y (t)) \\ x (t) & = t^{2} - 1 \\ y (t) & = 3 t^{3} \end{aligned}$

::查找以下t=0和t=10.G(t)=(x(t),y(t))x(t)=t2-1y(t)=3t3之间的曲线下区域

Find the area under the curve defined below between $\begin{aligned} t = 5 \end{aligned}$ and $\begin{aligned} t = 8 \end{aligned}$ .
$\begin{aligned} H (t) & = (x (t), y (t)) \\ x (t) & = 7 t \\ y (t) & = 3 t^{2} + 1 \end{aligned}$

::查找以下t=5和t=8.H(t)=(x(t),y(t))x(t)=7ty(t)=3t2+1之间的曲线下区域

Find the area under the curve defined below between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = 12 \end{aligned}$ .
$\begin{aligned} J (t) & = (x (t), y (t)) \\ x (t) & = t^{2} + 1 \\ y (t) & = t \end{aligned}$

::查找以下t=0和t=12.J(t)=(x(t),y(t))x(t)=t2+1y(t)=t的曲线下所定义的区域

For #5-8, find the area under the curve between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = \frac{π}{2} \end{aligned}$ .
::对于#5-8,在 t=0 和 t2 之间的曲线下找到区域。

$\begin{aligned} K (t) & = (x (t), y (t)) \\ x (t) & = 2 \cos (t) \\ y (t) & = 2 \sin (t) \end{aligned}$

:t)=(x(t),y(t))x(t)=2cos(t)y(t)=2sin(t)

$\begin{aligned} L (t) & = (x (t), y (t)) \\ x (t) & = 3 \cos (t) \\ y (t) & = 7 \sin (t) \end{aligned}$

:t)=(x(t),y(t))x(t)=3cos(t)y(t)=7sin(t)

$\begin{aligned} M (t) & = (x (t), y (t)) \\ x (t) & = 4 \cos (t) \\ y (t) & = \sin (t) \end{aligned}$

:t)=(x(t),y(t))x(t)=4cos(t)y(t)=sin(t)

$\begin{aligned} N (t) & = (x (t), y (t)) \\ x (t) & = 12 \cos (t) \\ y (t) & = 12 \sin (t) \end{aligned}$

:t)=(x(t),y(t))x(t)=12cos(t)y(t)=12sin(t)

For #9-15, find the area between the two curves for the given values of $\begin{aligned} t \end{aligned}$ .
::对于# 9-15, 找到 t 给定值在两个曲线之间的区域。

Between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = \frac{π}{2} \end{aligned}$ :
$\begin{aligned} P (t) & = (x (t), y (t)) \\ x (t) & = 12 \cos (t) \\ y (t) & = 8 \sin (t) \\ Q (t) & = (x (t), y (t)) \\ x (t) & = 10 \cos (t) \\ y (t) & = 8 \sin (t) \end{aligned}$

::t=0 和 t2: P(t) = (x(t) y(t) x(t) = 12cos * (t) y(t) = 8sin (t) Q(t) Q(t) = (x(t) y(t) x(t) = 10cos *(t) y(t) = 8sin(t)

Between $\begin{aligned} t = \frac{π}{2} \end{aligned}$ and $\begin{aligned} t = \frac{3 π}{2} \end{aligned}$ :
$\begin{aligned} R (t) & = (x (t), y (t)) \\ x (t) & = 3 \cos (t) \\ y (t) & = 3 \sin (t) \\ S (t) & = (x (t), y (t)) \\ x (t) & = \cos (t) \\ y (t) & = \sin (t) \end{aligned}$

::在 t2 和 t= 32: R( t) = (x( t) y( t) x( t) = 3cos ( t) y( t) = 3sin( t) S( t) (t) (t) = (x( t) y( t) x( t) = cos ( t) y( t) =sin( t)

Between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = π \end{aligned}$ :
$\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 10 \cos (t) \\ y (t) & = 10 \sin (t) \\ G (t) & = (x (t), y (t)) \\ x (t) & = 10 \cos (t) \\ y (t) & = 3 \sin (t) \end{aligned}$

::在 t= 0 和 t 之间 : F( t) = (x( t) ,y( t) ) x (t) = 10cos ( t) y( t) = 10sin( t) G( t) = (x( t) ,y( t) ) x( t) = 10cos ( t) y( t) = 3sin( t)

Between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = \frac{π}{2} \end{aligned}$ :
$\begin{aligned} H (t) & = (x (t), y (t)) \\ x (t) & = 8 \cos (t) \\ y (t) & = 10 \sin (t) \\ J (t) & = (x (t), y (t)) \\ x (t) & = 8 \cos (t) \\ y (t) & = 8 \sin (t) \end{aligned}$

::t=0 到 t2: H( t) = (x( t) y( t) x( t) = 8cos * (t) y( t) = 10sin (t) J( t) = (x( t) y( t) = (x( t) ,y( t) x( t) = 8sin ( t)

Between $\begin{aligned} t = \frac{π}{2} \end{aligned}$ and $\begin{aligned} t = π \end{aligned}$ :
$\begin{aligned} K (t) & = (x (t), y (t)) \\ x (t) & = 12 \cos (t) \\ y (t) & = 12 \sin (t) \\ L (t) & = (x (t), y (t)) \\ x (t) & = 5 \cos (t) \\ y (t) & = 5 \sin (t) \end{aligned}$

::t2 和 t : K( t) = (x( t) ,y( t) ) x( t) = 12cos ( t) y( t) = 12sin( t) (t) L( t) = (x( t) ,y( t) = 5cos ( t) = 5sin( t)

Between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = π \end{aligned}$ :
$\begin{aligned} M (t) & = (x (t), y (t)) \\ x (t) & = 8 \cos (t) \\ y (t) & = 7 \sin (t) \\ N (t) & = (x (t), y (t)) \\ x (t) & = 6 \cos (t) \\ y (t) & = 5 \sin (t) \end{aligned}$

::t=0 和 t : M(t) = (x(t) y(t) ) x(t) = 8cos *(t) y(t) = 7sin *(t) N(t) = (x(t) y(t) x(t) = 6cos *(t) y(t) y(t) = 5sin(t)

Between $\begin{aligned} t = 0 \end{aligned}$ and $\begin{aligned} t = 2 π \end{aligned}$ :
$\begin{aligned} P (t) & = (x (t), y (t)) \\ x (t) & = 3 \cos (t) \\ y (t) & = 3 \sin (t) \\ Q (t) & = (x (t), y (t)) \\ x (t) & = 3 \cos (t) \\ y (t) & = \sin (t) \end{aligned}$

::在 t= 0 和 t= 2之间: P( t) = (x( t) ,y( t) ) x( t) = 3cos ( t) y( t) = 3sin( t) Q( t) Q( t) = (x( t) y( t) x( t) = 3cos ( t) y( t) =sin( t)

Review (Answers)
::回顾(答复)
To see the answer key for this book, go to the and click on the Answer Key under the ' ' option.

章节大纲

Area Under a Parametric Curve ::参数曲线下的区域

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Area Under a Parametric Curve
::参数曲线下的区域

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)