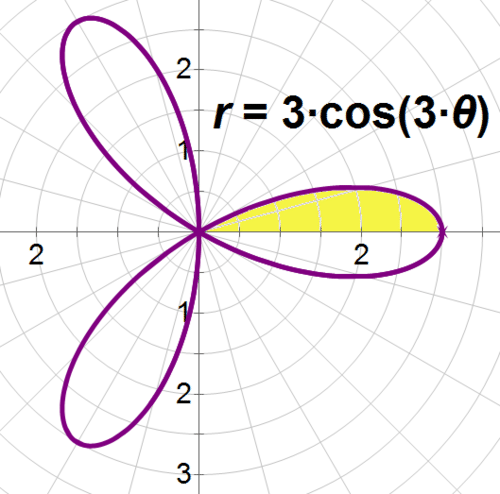节: 极表和微积分:平地面积 | 10.13 极表和微积分:平面面积

章节大纲

Max has just finished setting up the microphones and speakers for his sister’s wedding reception. He gets a frantic text from the best man. The groomsmen have planned a special song and dance routine to pay homage to the couple’s love of acapella music. The number must be carefully choreographed, and the groomsmen need to know how much room they have to sing and dance. All 7 of them want to be careful to stay within the range of the microphones. Can Max give them an accurate number for the floor area they have without measuring by hand? The wedding starts in less than an hour, so he needs to have an answer soon.
::马克斯刚刚为他姐姐的婚礼招待会安装了麦克风和扬声器。他得到了伴郎发来的疯狂短信。新郎们计划了一场特殊的歌曲和舞蹈活动,以向这对夫妇对阿卡贝拉音乐的爱致敬。这个数字必须仔细编程,而且新郎们需要知道他们有多少空间可以唱歌和跳舞。他们中的7人都想小心地留在麦克风的范围之内。 Max能否给他们一个不手工测量的地面面积的准确数字? 婚礼在不到一个小时内开始,所以他需要尽快得到答案。

Area with Polar Form
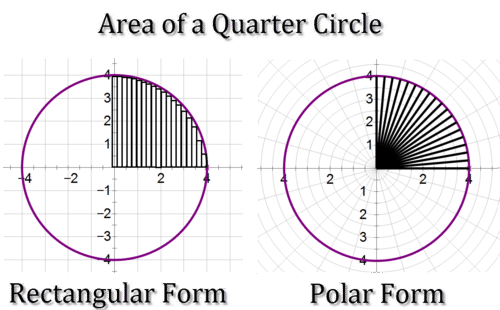
::极表区域

When you find the area under a curve in rectangular form , you’re measuring the amount of space between the curve and the $\begin{aligned} x \end{aligned}$ -axis. To find the area, you’re essentially dividing the curve into an infinite number of infinitely thin rectangles. By finding the sum of the areas of all the rectangles, you can find the area under the entire curve.
::当您在矩形曲线下找到区域时,您正在测量曲线和 X 轴之间的间距。要找到区域,您基本上就把曲线分割成无限细的矩形。通过找到所有矩形区域的总和,您就可以在整个曲线下找到区域。

When you find the area under a curve in polar form , you’re finding the area of the space bounded by the curve and two rays that share a common origin. You’re finding the area enclosed by an infinite number of infinitely small sectors.
::当您在极曲线下找到区域时,您正在找到与曲线和两条共同来源的射线相邻的空间区域。您正在找到被无限小的区块所包围的区域。

The formula for the area under a curve in polar form takes this difference into account. To find the area under a curve in polar form, you use the formula $\begin{aligned} A = \int_{a}^{b} {(ρ (θ))}^{2} d θ \end{aligned}$ , where $\begin{aligned} ρ (θ) \end{aligned}$ is the radius $\begin{aligned} r \end{aligned}$ . So, for instance, to find the area under the curve $\begin{aligned} r = 2 θ \end{aligned}$ from 0 to $\begin{aligned} π \end{aligned}$ , you’d integrate the following: $\begin{aligned} A = \int_{0}^{π} \frac{1}{2} {(2 θ)}^{2} d θ \end{aligned}$ .
::极形曲线下区域的公式考虑到这一差异。要找到极形曲线下的区域,请使用公式 Aab( }) 2d, 其中是半径 r 。因此, 例如, 要在 r= 2( 从 0 到 ) 的曲线下找到区域, 您可以将以下区域整合到 : A0 12( 2) 2d 中。

Finding the area under a polar curve can be a bit more complicated than finding the area under a rectangular curve. First, determine what sort of curve the equation represents. Then sketch the curve and figure out what angles of $\begin{aligned} θ \end{aligned}$ form the boundaries of the area you plan to integrate (be very careful with this step!). Finally, set up the integrals and solve.
::在极曲线下查找区域可能比在矩形曲线下查找区域要复杂一些。首先, 确定方程代表的曲线类型。然后绘制曲线图, 并找出% 的角构成您计划整合的区域的边界( 要非常小心此步骤 !) 。最后, 设置整体和解析。

Now, let's apply that technique to fi nd the area inside the polar curve $\begin{aligned} r = 1 + \cos θ \end{aligned}$ .
::现在,让我们运用这个技术找到极曲线 r=1+cos内的区域。

This equation appears to be a cardioid. Graph the curve to be sure.
::此方程式似乎是一个类固醇。绘制曲线以确认。

Notice that this curve is symmetrical. This means that the area from 0 to $\begin{aligned} π \end{aligned}$ is half the area inside the entire curve. So one way to find the area is to integrate from 0 to $\begin{aligned} π \end{aligned}$ , and then double the result.
::注意此曲线是对称的。这意味着 0 到 __ 的区域是整个曲线内区域的一半。因此找到区域的一个方法就是将区域从 0 到 __ 合并, 然后将结果翻一番。

$\begin{aligned} A & = \int_{a}^{b} \frac{1}{2} {(ρ (θ))}^{2} d θ \\ = 2 \int_{0}^{π} \frac{1}{2} (1 + \cos θ)^{2} d θ \\ = \int_{0}^{π} (1 + 2 \cos θ + \cos^{2} θ) d θ \end{aligned}$

::============================================================================================================================================= ===============================================================================================================================================================================================================================================================================================================================================================================

Use a trigonometric identity to simplify $\begin{aligned} \cos^{2} θ \end{aligned}$ .
::使用三角特征来简化 Cos2。

$\begin{aligned} = \int_{0}^{π} (1 + 2 \cos θ + \cos^{2} θ) d θ \\ = \int_{0}^{π} (1 + 2 \cos θ + \frac{1}{2} + \cos (2 θ)) d θ \\ = {[\frac{3 θ}{2} + 2 \sin θ + \frac{1}{2} \sin (2 θ)]}_{0}^{π} \\ = \frac{3 π}{2} \\ A & = \frac{3 π}{2} u n i t s^{2} \end{aligned}$

::0( 1+2cos2) d( 1+2cos12+cos22222222222222222222222222222222222222222222222222

Examples
::实例

Example 1
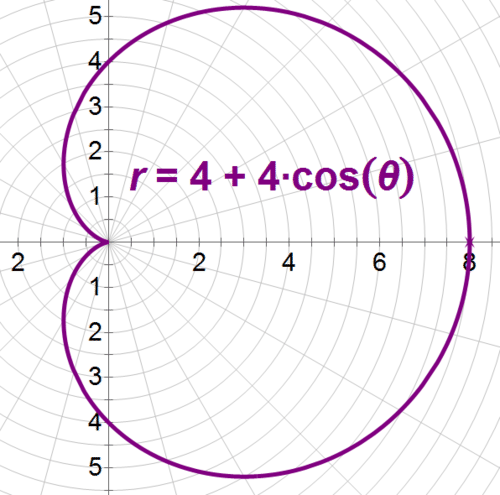
::例1

Earlier, you were asked how Max can determine how much area on the dance floor the groomsmen will have so that they will remain in range of the microphones. Max contacts the manufacturer and finds out that one of his microphones is a cardioid microphone with a pickup area of $\begin{aligned} r = 4 + 4 \cos θ \end{aligned}$ with the distance measured in feet. He graphs the equation and sees that the groomsmen can stand up to eight feet behind the microphone and still be heard.
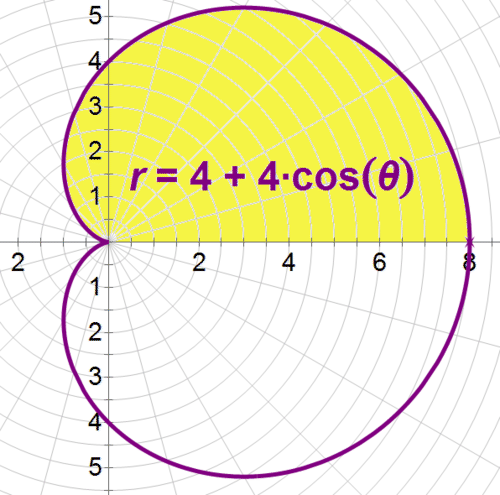
::早些时候,有人问您Max如何确定舞蹈地板上的新郎们有多少面积,以便留在麦克风的射程内。 Max联系了制造商,发现他的一个麦克风是一个心型麦克风,有r=4+4cos的接合区,有以足为单位的距离。他绘制了方程图,看到新郎们可以站到麦克风后面8英尺,仍然可以听到。

Since the microphone’s range is symmetrical, Max can find the area from 0 to $\begin{aligned} π \end{aligned}$ , as shown below, and then double it.
::因为麦克风的射程是对称的, Max可以找到0到%的区域, 如下文所示, 然后翻一番。

$\begin{aligned} A & = \int_{a}^{b} \frac{1}{2} {(ρ (θ))}^{2} d θ \\ = 2 \int_{0}^{π} \frac{1}{2} {(4 + 4 \cos θ)}^{2} d θ \\ = \int_{0}^{π} (16 + 8 \cos θ + 16 \cos^{2} θ) d θ \\ = 16 \int_{0}^{π} (1 + \frac{1}{2} \cos θ + \cos^{2} θ) d θ \\ = 16 \int_{0}^{π} (1 + \frac{1}{2} \cos θ + \frac{1}{2} + \cos 2 θ) d θ \\ = 16 {[\frac{3 θ}{2} + \frac{1}{2} \sin θ + \frac{1}{2} \sin 2 θ]}_{0}^{π} \\ = 24 π \end{aligned}$

::======================================================================================================================================================

The groomsmen have $\begin{aligned} 24 π \end{aligned}$ , or about 75 square feet, of floor space to perform their act.
::新郎们有24平方英尺或约75平方英尺的地板空间来表演他们的行为。

Example 2
::例2

Find the area enclosed by the polar curve $\begin{aligned} r = 3 \cos (3 θ) \end{aligned}$ .
::查找极曲线 r= 3cos(3) 所覆盖的区域。

This is a rose curve with 3 petals. Sketch or graph the curve so that you can see where to integrate.
::这是一个包含 3 个花瓣的玫瑰曲线。拖动或绘制曲线图, 以便您看到如何整合。

When theta is zero, the radius is 1. When theta is $\begin{aligned} \frac{π}{6} \end{aligned}$ , the radius is zero. You can see from the graph that this interval will give the area of half a petal.
::当Theta为零时,半径为1。当theta为 6时,半径为 6。从图表中可以看出,这个间距会给半个花瓣面积。

Since there are 3 petals, if you multiply the area of the half-petal by six, you’ll find the area enclosed by the entire curve.
::因为有3个花瓣, 如果你把半块半块的面积乘以6, 就会发现整个曲线所覆盖的区域。

$\begin{aligned} A & = \int_{a}^{b} \frac{1}{2} {(ρ (θ))}^{2} d θ \\ = 6 \int_{0}^{\frac{π}{6}} \frac{1}{2} {(3 \cos (3 θ))}^{2} d θ \\ = 3 \int_{0}^{\frac{π}{6}} {(3 \cos (3 θ))}^{2} d θ \\ = 27 \int_{0}^{\frac{π}{6}} \cos^{2} (3 θ) d θ \end{aligned}$

::-=YTET -伊甸园字幕组=-伊甸园字幕组=- 翻译:

Simplify using the trigonometric identity: $\begin{aligned} \cos^{2} θ = \frac{1}{2} + \frac{1}{2} \cos 2 θ \end{aligned}$ .
::使用三角特性简化 : cos2\\\ 12+12cos\\\ 2 。

$\begin{aligned} A & = 27 \int_{0}^{\frac{π}{6}} \cos^{2} (3 θ) d θ \\ = 27 \int_{0}^{\frac{π}{6}} \frac{1}{2} + \frac{1}{2} \cos (6 θ) d θ \\ = \frac{27}{2} \int_{0}^{\frac{π}{6}} 1 + \cos (6 θ) d θ \\ = \frac{27}{2} {[θ + \frac{1}{6} \sin (6 θ)]}_{0}^{\frac{π}{6}} \\ = \frac{9 π}{4} u n i t s^{2} \end{aligned}$

::A=2706cos2(3)d270612+12cos(6)d272061+cos(6)d272[16sin(6)]06=94单位2

Example 3
::例3

Find the area of the space between the polar curves $\begin{aligned} r = 1 + \cos θ \end{aligned}$ and $\begin{aligned} r = \cos θ \end{aligned}$ .
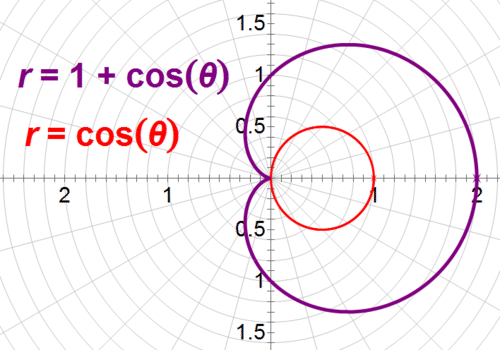
::查找极曲线 r= 1+cos 和 r= cos 之间的空间区域。

You may recognize $\begin{aligned} r = 1 + \cos θ \end{aligned}$ from Example A. It is a cardioid curve. Meanwhile, $\begin{aligned} r = \cos θ \end{aligned}$ produces a circle in polar form. Graph the two curves together so that you can see the space and its boundaries.
::您可以从例A中识别 r=1+cos。它是一个心形曲线。同时, r=cos 以极的形式产生圆形。将两个曲线一起绘制, 以便您可以看到空间及其边界。

As you can see, $\begin{aligned} r = \cos θ \end{aligned}$ is totally enclosed by $\begin{aligned} r = 1 + \cos θ \end{aligned}$ . This means that you can simply find the area of $\begin{aligned} r = \cos θ \end{aligned}$ and subtract it from the area of $\begin{aligned} r = 1 + \cos θ \end{aligned}$ . You already know that the area enclosed by $\begin{aligned} r = 1 + \cos θ \end{aligned}$ is $\begin{aligned} \frac{3 π}{2} \end{aligned}$ . To find the area of $\begin{aligned} r = \cos θ \end{aligned}$ , calculate the area from 0 to $\begin{aligned} \frac{π}{2} \end{aligned}$ (which gives you the top half of the circle) and then multiply it by 2.
::正如您所看到的, r=cos 完全被 r= 1+cos 附加。这意味着您可以简单地找到 r=cos 区域, 从 r= 1+cos 区域中减去 r= 1+cos 区域。您已经知道 r= 1+cos 区域是 32 。要找到 r=cos 区域, 请计算区域从 0 到 2 (给您带来圆的上半部分) , 然后乘以 2 。

$\begin{aligned} A & = \int_{a}^{b} \frac{1}{2} {(ρ (θ))}^{2} d θ \\ = 2 \int_{0}^{\frac{π}{2}} \frac{1}{2} (\cos θ)^{2} d θ \\ = \int_{0}^{\frac{π}{2}} \cos^{2} θ d θ \\ = \int_{0}^{\frac{π}{2}} \frac{1}{2} + \frac{1}{2} \cos 2 θ d θ \\ = \frac{1}{2} \int_{0}^{\frac{π}{2}} 1 + \cos 2 θ d θ \\ = \frac{1}{2} {[θ + \frac{1}{2} \sin 2 θ]}_{0}^{\frac{π}{2}} \\ = \frac{π}{4} \end{aligned}$

::======================================================================================================================================================

Remember, the cardioid had an area of $\begin{aligned} \frac{3 π}{2} \end{aligned}$ , so the area between the curves is $\begin{aligned} \frac{5 π}{4} \end{aligned}$ .
::记住,心血管的面积是3°2, 所以曲线之间的面积是5°4。

Example 4
::例4

Find the area of the space enclosed by $\begin{aligned} r = \frac{θ}{4} \end{aligned}$ from 0 to $\begin{aligned} \frac{3 π}{2} \end{aligned}$ .
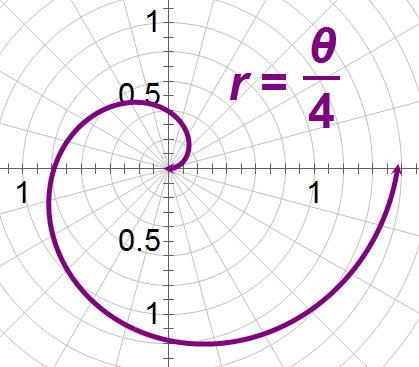
::寻找由 r4 从 0 到 32 所附加的空间面积。

This equation describes an Archimedean spiral.
::这个方程式描述的是Archimedean螺旋螺旋。

You are finding the area from 0 to $\begin{aligned} \frac{3 π}{2} \end{aligned}$ , as shown shaded below.
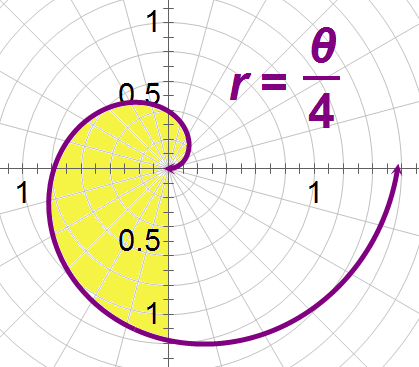
::您正在从 0 到 3°2 找到区域, 如下面的阴影所示。

Use the area formula and integrate. It is not symmetrical, so you’ll have to integrate the entire range at once.
::使用区域公式并整合。它不是对称的, 所以您必须同时整合整个范围。

$\begin{aligned} A & = \int_{a}^{b} \frac{1}{2} {(ρ (θ))}^{2} d θ \\ = \int_{0}^{\frac{3 π}{2}} \frac{1}{2} {(\frac{θ}{4})}^{2} d θ \\ = \int_{0}^{\frac{3 π}{2}} \frac{1}{2} \cdot \frac{θ^{2}}{16} d θ \\ = \frac{1}{32} \int_{0}^{\frac{3 π}{2}} θ^{2} d θ \\ = \frac{1}{32} {[\frac{θ^{3}}{3}]}_{0}^{\frac{3 π}{2}} \\ = \frac{9 π^{3}}{256} u n i t s^{2} \end{aligned}$

::ab122d03212( 4)2d03212216d132032222132[ 33]032=93256units2

Example 5
::例5

Find the area of the space between $\begin{aligned} r = 5 \cos 5 θ \end{aligned}$ and $\begin{aligned} r = 5 \end{aligned}$ .
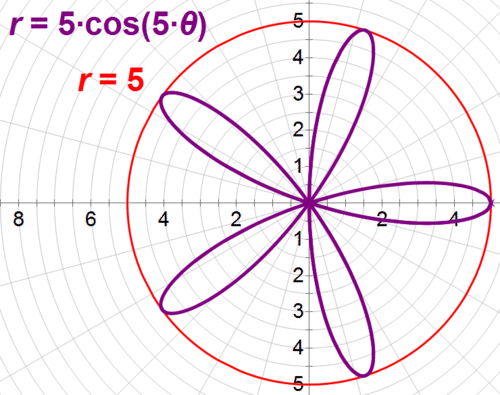
::查找 r= 5cos 5 5 和 r= 5 之间的空间区域。

This graph is of a rose curve enclosed by a circle.
::本图为圆环所环绕的玫瑰曲线。

Find the area of the circle and subtract the area enclosed by the rose curve. The area of the circle is:
::查找圆区域,减去玫瑰曲线所覆盖的区域。圆区域是:

$\begin{aligned} A & = \int_{a}^{b} \frac{1}{2} {(p (θ))}^{2} d θ \\ = 2 \int_{0}^{π} \frac{1}{2} (5)^{2} d θ \\ = \int_{0}^{π} 25 d θ \\ = 25 π \end{aligned}$

::Aab12(p())2d______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Note that this is the same result as if you'd used the traditional formula for the area of a circle, $\begin{aligned} A = π r^{2} \end{aligned}$ . To find the area of the rose curve, find the area of one half of a petal (shown below) and multiply by 10.
::请注意,这个结果与您使用的圆区域传统公式Ar2相同。要找到玫瑰曲线区域, 请找到花瓣面积的一半( 如下所示), 乘以 10 。

The area of the rose curve is:
::玫瑰曲线的面积是:

$\begin{aligned} A & = 10 \int_{a}^{b} \frac{1}{2} {(ρ (θ))}^{2} d θ \\ = 10 \int_{0}^{\frac{π}{10}} \frac{1}{2} {(5 \cos 5 θ)}^{2} d θ \\ = 125 \int_{0}^{\frac{π}{10}} \cos^{2} (5 θ) d θ \\ = 125 \int_{0}^{\frac{π}{10}} (\frac{1}{2} + \frac{1}{2} \cos (10 θ)) d θ \\ = 125 {[\frac{θ}{2} + \frac{\sin (10 θ)}{20}]}_{0}^{\frac{π}{10}} \\ = 125 (\frac{π}{20}) \\ = \frac{25 π}{4} \end{aligned}$

::A=10ab122d1000102( 5cos552)2d125010cos2( 5)d125010( 12+12cos( 10))d125[ 2+sin( 1020)]010=125( 20)=254

So, the area between the two shapes is:
::因此,两种形状之间的区域是:

$\begin{aligned} 25 π - \frac{25 π}{4} = \frac{75 π}{4} u n i t s^{2} \end{aligned}$
::25254=754单位2

Review
::回顾

Find the area inside the polar curve $\begin{aligned} r = 4 + 4 \cos θ \end{aligned}$ .
::查找极曲线 r=4+4cos中的区域。

Find the area enclosed by the polar curve $\begin{aligned} r = 6 \cos 2 θ \end{aligned}$ .
::找到极曲线 r=6cos22所覆盖的区域。

Find the area of the space enclosed by $\begin{aligned} r = \frac{1}{10} θ \end{aligned}$ from 0 to $\begin{aligned} π \end{aligned}$ .
::查找由 r= 110从 0 到 ° 所填充的空间面积。

Find the area of $\begin{aligned} r = 2 \sin 6 θ \end{aligned}$ from 0 to $\begin{aligned} \frac{π}{6} \end{aligned}$ .
::查找 r= 2sin\\\\\\\\\\\ n6\\\\\\\\\\\\\\\\\\\\\\\\\\\\§6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Find the area inside $\begin{aligned} r = 2 + 2 \cos θ \end{aligned}$ .
::在 r=2+2cos中查找区域。

Find the area inside one petal of $\begin{aligned} r = \sin 4 θ \end{aligned}$ .
::在R=sin4的一个花瓣内找到区域。

Find the area inside one petal of $\begin{aligned} r = \cos 5 θ \end{aligned}$ .
::在R=cos5的一个花瓣内找到区域。

Find the area inside one petal of $\begin{aligned} r = \cos 2 θ \end{aligned}$ .
::在R=cos2的一个花瓣内找到区域。

Find the area bounded by $\begin{aligned} r = 4 \cos θ \end{aligned}$ , $\begin{aligned} 0 \leq θ \leq π \end{aligned}$ .
::找到被 r=4cos,0 所包围的区域。

Find the area inside $\begin{aligned} r = 2 + 2 \cos θ \end{aligned}$ and outside $\begin{aligned} r = 2 \end{aligned}$ .
::在 r= 2+2cos 和 r= 2 外 r 中查找区域。

Find the area inside $\begin{aligned} r = \cos θ \end{aligned}$ and outside $\begin{aligned} r = 1 - \sin θ \end{aligned}$ .
::在r=cos和外部r=1-sin中找到区域。

Find the area enclosed by $\begin{aligned} r = \frac{θ}{2} \end{aligned}$ from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::查找由 r2 从 0 到 2 的区域。

Find the area enclosed by $\begin{aligned} r = a \end{aligned}$ from 0 to $\begin{aligned} 2 π \end{aligned}$ . What does this have to do with the geometry formula $\begin{aligned} A = π r^{2} \end{aligned}$ ?
::查找 r=a 从 0 到 2 的区域。这与 Ar2 几何公式有什么关系 ?

Find the area of the space between $\begin{aligned} r = 3 \cos 4 θ \end{aligned}$ and $\begin{aligned} r = 3 \end{aligned}$ .
::查找 r= 3cos4 和 r=3 之间的空间区域。

Find the area of the space between the polar curves $\begin{aligned} r = 1 + \sin θ \end{aligned}$ and $\begin{aligned} r = \sin θ \end{aligned}$ .
::查找极曲线 r=1+sin 和 r=sin 之间的空间区域。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Area with Polar Form ::极表区域

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Area with Polar Form
::极表区域

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)