Course: 8.19 翻译、轮换和反思

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 翻译、轮换和反思

Collapse Expand
翻译、轮换和反思
Tyler takes a picture of an item and its reflection . He places a coordinate plane over the picture. The coordinate plane is positioned so that the $\begin{aligned} x - \end{aligned}$ axis separates the image from the reflection. He then makes the grid according to the key features of the picture, so that a point at (2, 0) is reflected at the point (-2, 0). If the original coordinates of the image are (3, 0), (4, 6) and (5, 1), what are the coordinates of the reflection?
::泰勒拍摄了一个项目及其反射。他在图片上放置一个坐标平面。坐标平面的位置是 x- 轴将图像与反射分开。然后他根据图像的关键特征绘制网格, 从而在点( 2, 0) 上显示一个点( 2, 0) 。如果图像的原始坐标是 (3, 0, 4, 6) 和 (5, 1) , 反射的坐标是什么 ?

In this concept, you will learn how to find the coordinates for translations, rotations and reflections .
::在这个概念中,你将学会如何找到翻译、轮换和思考的坐标。

Finding Coordinates for Translations, Rotations, and Reflections
::翻译、轮换和反省查找坐标

When you perform translations, you slide a figure left or right, up or down. This means that on the coordinate plane, the coordinates for the vertices of the figure will change.
::当您进行翻译时,您会向上或向下或向左滑动一个图。这意味着在坐标平面上,图顶的坐标将会改变。

To graph a translation, perform the same change for each point.
::要绘制一个翻译图,请对每个点执行相同的修改。

You can identify a reflection by the changes in its coordinates. In a reflection , the figure flips across a line to make a mirror image of itself. Take a look at the reflection below.
::您可以通过坐标的修改来辨别反射。在反射中, 图形翻过一条线, 以形成反射图像。请看看下面的反射。

Figures are usually reflected across either the $\begin{aligned} x - \end{aligned}$ or the $\begin{aligned} y - \end{aligned}$ axis. In this case, the figure is reflected across the $\begin{aligned} y - \end{aligned}$ axis . If you compare the figures in the first example vertex by vertex, you see that the $\begin{aligned} x - \end{aligned}$ coordinates change but the $\begin{aligned} y - \end{aligned}$ coordinates stay the same. This is because the reflection happens from left to right across the $\begin{aligned} y - \end{aligned}$ axis. When you reflect across the $\begin{aligned} x - \end{aligned}$ axis, the $\begin{aligned} y - \end{aligned}$ coordinates change and the $\begin{aligned} x - \end{aligned}$ coordinates stay the same. Take a look at this example.
::数字通常在 x - 或 y - 轴中反映。在这种情况下,该数字在 y - 轴中反映。如果用顶点比较第一个示例顶点中的数字,你会看到 x - 坐标变化,但 y - 坐标保持不变。这是因为反射从左到右在 y - 轴中发生。当您在 x - 轴中反映时, y - 坐标变化和 x - 坐标保持不变。看看这个例子。

In the figure above the coordinates for the upper-left vertex of the original figure are (-5, 5). After you reflect it across the $\begin{aligned} x - \end{aligned}$ axis, the coordinates for the corresponding vertex are (-5, -5). How about the lower-right vertex? It starts out at (-1, 1), and after the flip it is at (-1, -1). As you can see, the $\begin{aligned} x - \end{aligned}$ coordinates stay the same while the $\begin{aligned} y - \end{aligned}$ coordinates change. In fact, the $\begin{aligned} y - \end{aligned}$ coordinates all become the opposite integers of the original $\begin{aligned} y - \end{aligned}$ coordinates. This indicates that this is a vertical (up/down) reflection or a reflection over the $\begin{aligned} x - \end{aligned}$ axis.
::在原图左上角的坐标( 5, 5) 上方的坐标上方是 (5, 5) 。在反射 X - 轴时, 相应的顶端的坐标是 (5, 5, 5) , 右下端的顶端的坐标是 (1, 1) 如何? 在( 1- 1) 开始, 翻转后( 1, 1- 1) 。正如你所看到的, x - 坐标保持不变, 而 y - 坐标则变化。事实上, y - 坐标都成了 y - 坐标的反向整数。这表示这是垂直的( 上下) 反射或反射 x - 轴的反射。

In a horizontal (left/right) reflection or a reflection over the $\begin{aligned} y - \end{aligned}$ axis, the $\begin{aligned} x - \end{aligned}$ coordinates would become integer opposites. Let’s look at an example.
::在Y-轴的横向(左/右)反射或反射中,x-坐标将变成整形反向。让我们来举一个例子。

This is a reflection across the $\begin{aligned} y - \end{aligned}$ axis. Compare the points. Notice that the $\begin{aligned} y - \end{aligned}$ coordinates stay the same. The $\begin{aligned} x - \end{aligned}$ coordinates become the integer opposites of the original $\begin{aligned} x - \end{aligned}$ coordinates. Look at the top point of the triangle , for example. The coordinates of the original point are (-4, 6), and the coordinates of the new point are (4, 6). The $\begin{aligned} x - \end{aligned}$ coordinate has switched from -4 to 4.
::这是横跨 y- 轴的反射。比较各点。请注意, y- 坐标保持不变。 x- 坐标变成原始 x- 坐标的整数对面。例如, 查看三角形的顶点。原点的坐标是 (4 、 6) , 新点的坐标是 (4 、 6) 。 x- 坐标已经从 - 4 切换为 4 。

You can recognize reflections by these changes to the $\begin{aligned} x - \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ coordinates. If you reflect across the $\begin{aligned} x - \end{aligned}$ axis, the $\begin{aligned} y - \end{aligned}$ coordinates will become opposite. If you reflect across the $\begin{aligned} y - \end{aligned}$ axis, the $\begin{aligned} x - \end{aligned}$ coordinates will become opposite.
::您可以通过对 x - 和 y - 坐标线的这些变化来识别反射。如果您在 x - 轴线上反射, y - 坐标线就会反射。如果您在 y - 轴线上反射, x - 坐标线就会反射。

You can also use this information to graph reflections. To graph a reflection, you need to decide whether the reflection will be across the $\begin{aligned} x - \end{aligned}$ axis or the $\begin{aligned} y - \end{aligned}$ axis, and then change either the $\begin{aligned} x - \end{aligned}$ or $\begin{aligned} y - \end{aligned}$ coordinates.
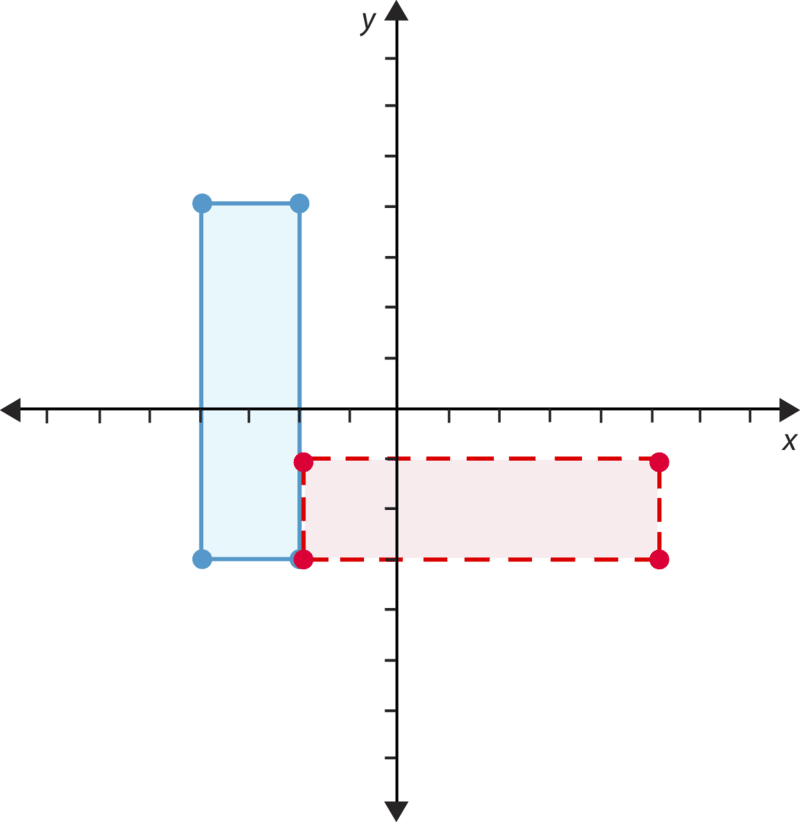
::您也可以用此信息绘制反射图。要绘制反射图,您需要决定反射是横跨 x - 轴还是y - 轴,然后修改 x - 或 y - 坐标。

Now let’s look at the third kind of transformation: rotations. A rotation is a transformation that turns the figure in either a clockwise or counterclockwise direction. The figure below has been rotated. What are its new coordinates?
::现在让我们看看第三种变换类型:轮转。轮转是一个将数字转换成时钟方向或反时钟方向的变换。下图已被旋转。它的新坐标是什么?

The new coordinates of the rectangle’s vertices are (1, -3), (1, 2), (3, 2), and (3, -3). As you can see, both the $\begin{aligned} x - \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ coordinates changed. One of the points remained exactly the same. That means the figure was rotated about this point. Imagine you put your finger on this corner of the rectangle and spun it. That’s what happened in the rotation. The rectangle has been rotated $\begin{aligned} 90^{\circ} \end{aligned}$ clockwise.
::矩形顶端的新坐标是(1, - 3, 1, 2, 3, 2) 和 (3, 2) 以及 (3, 3, 3) 。正如您所看到的, x - 和 y - 座标都变了。其中的一个点保持不变。这意味着此点的数字是旋转的。想象一下您将手指放在矩形的角上, 并按时序旋转。这就是旋转时发生的情况。矩形已经旋转了 90 % 。

When you graph a rotation, you first need to know how much the figure will be rotated. Rotating the rectangle above $\begin{aligned} 90^{\circ} \end{aligned}$ stands it up on end. Rotating it $\begin{aligned} 180^{\circ} \end{aligned}$ would make it flat again. You also need to know which point you will rotate it around. This is the point that stays the same.
::当您绘制一个旋转图时,您首先需要知道数字会旋转多少。旋转90以上矩形时, 旋转90以上矩形时, 旋转90以上矩形时, 旋转90以上矩形时, 旋转90以上矩形时, 旋转90以上矩形时, 旋转90以上矩形时, 旋转90。旋转180时, 它会再次平坦。您也需要知道您要旋转哪个点。这是保持不变的点。

Next, you need to count how many units long and wide the figure is. The figure above stretches from 1 on the $\begin{aligned} x - \end{aligned}$ axis to -4 on the $\begin{aligned} x - \end{aligned}$ axis. This is a total of 5 units along the $\begin{aligned} x - \end{aligned}$ axis. When you rotate a figure $\begin{aligned} 90^{\circ} \end{aligned}$ , the distance on the $\begin{aligned} x - \end{aligned}$ axis becomes the distance on the $\begin{aligned} y - \end{aligned}$ axis. Look at the rectangle. The long sides are horizontal at first, but after you rotate it, they become the vertical sides. This means that the $\begin{aligned} x - \end{aligned}$ distance of 5 will become a $\begin{aligned} y - \end{aligned}$ distance of 5.
::接下来,您需要计算数字的长度和宽度。上方的数字从x- 轴的1个单位到x- 轴的4个单位。这在x- 轴上总共是5个单位。当您旋转一个图 90 时, x- 轴的距离会成为 y- 轴的距离。看看矩形。长边起初是水平的, 但在您旋转后, 它们会变成垂直的两边。这意味着 x- 距离 5 将变成 y- 距离 5 。

Now, remember the point (1, -3) stays the same, so it is one corner of the rotated figure. You add 5 to the $\begin{aligned} y - \end{aligned}$ coordinate to find the next vertex of the rectangle. $\begin{aligned} - 3 + 5 = 2 \end{aligned}$ . This puts a vertex at (1, 2).
::现在, 请记住点(1, 3) 保持不变, 所以它是旋转图的一个角。您可以在 y - 坐标中添加 5 , 以找到矩形的下一个顶点。 - 3+ 5= 2 。这将在 1, 2 处设置一个顶点。

To find the other points of the rotated rectangle, you need to think about its width. Find the width, or short side, of the original rectangle by counting the units between vertices along the $\begin{aligned} y - \end{aligned}$ axis. The rectangle covers 2 units on the $\begin{aligned} y - \end{aligned}$ axis. As you might guess, this becomes the $\begin{aligned} x - \end{aligned}$ distance in the rotated figure. In other words, you add 2 to the $\begin{aligned} x - \end{aligned}$ coordinate of the point that stays the same. $\begin{aligned} 1 + 2 = 3 \end{aligned}$ , so another vertex of the rectangle will be (3, -3). To find the fourth and final vertex, add 2 to the $\begin{aligned} x - \end{aligned}$ coordinate of the other ordered pair, (1, 2). This puts the last vertex at (3, 2).
::要找到旋转矩形的其他点, 您需要考虑旋转矩形的宽度。找到正方形的宽度或短边, 通过计算y- 轴的顶部之间的单位。矩形覆盖 y- 轴的 2 个单位。正如您可能猜想的, 这在旋转的图形中成为 x - 距离。换句话说, 您要在点的x - 坐标中添加 2 个, 保持不变。 1+2= 3, 这样矩形的另一个顶部将是 (3, - 3) 。要找到第四个和最后一个顶部, 在其他订购的对的 x - 坐标中增加 2 个 (1, 2 ) 。这将将最后一个顶部放在 (3, 2) 。

Write each set of coordinates to show a reflection in the $\begin{aligned} y - \end{aligned}$ axis.
::写下每组坐标以显示 Y - 轴的反射。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Tyler and his picture.
::早些时候,你得到一个问题关于泰勒和他的照片。

If the original coordinates of the image are (3, 0), (4, 6) and (5, 1), what are the coordinates of the reflection?
::如果图像的原始坐标是(3,0),(4,6)和(5,1),反射的坐标是多少?

First, remember how to reflect across the $\begin{aligned} x - \end{aligned}$ axis.
::首先,记住如何反射 X - 轴。

Flip the shape across the $\begin{aligned} x - \end{aligned}$ axis.
::将形状翻转到 X - 轴上。

Next, remember the rules.
::接下来,记住规则

The $\begin{aligned} y - \end{aligned}$ coordinates will change to their integer opposites.
::Y - 坐标将改变为整数反方向。

Then, write the new points.
::然后写下新的点数。

(3, 0), (4, -6), (5, -1)

The answer is that the coordinates of the reflection are (3, 0), (4, -6), (5, -1).
::答案是,反射的坐标是(3,0),(4,6),(5,1),(4,6),(3,0),(5,1)。

Example 2
::例2

The figure below is reflected across the $\begin{aligned} x - \end{aligned}$ axis. What are the coordinates of the reflection?
::下图横跨x-轴,反映了下图。反射的坐标是多少?

First, remember how to reflect across the $\begin{aligned} x - \end{aligned}$ axis.
::首先,记住如何反射 X - 轴。

Flip the shape across the $\begin{aligned} x - \end{aligned}$ axis.
::将形状翻转到 X - 轴上。

Next, remember the rules.
::接下来,记住规则

The $\begin{aligned} y - \end{aligned}$ coordinates will change to their integer opposites.
::Y - 坐标将改变为整数反方向。

Then, write the new points.
::然后写下新的点数。

(3, -6), (3, -1), (5, -6), (5, -1)

The answer is that the coordinates of the reflection are (3, -6), (3, -1), (5, -6), (5, -1).
::答案是,反射的坐标是(3,6),(3,1),(5,6),(5,1),(5,1)。

Example 3
::例3

Determine if the change is the result of a translation, reflection or rotation.
::确定更改是翻译、反思或轮换的结果。

After a transformation, the vertices (3, 1), (0, 3), (1, 2) become (3, -1), (0, -3), (1, -2).
::转变后,顶点(3,1),(0,3),(1,2)变成(3,1),(0,3),(1,2),(1),(1,2),(1,2),(3),(3),(3),(3),(3),(2),(1,2)。

First, look at the coordinates to see which coordinate changes.
::首先,看看坐标,看哪个坐标能协调变化。

The $\begin{aligned} x - \end{aligned}$ coordinates stay the same and the $\begin{aligned} y - \end{aligned}$ coordinates change for each of the points.
::x- 坐标保持不变, y- 坐标对每个点都有变化。

Next, determine the type of change for the coordinates.
::下一步,确定坐标的更改类型。

The new $\begin{aligned} y - \end{aligned}$ coordinates are opposites of the original coordinates.
::新的Y座标与原来的座标相反。

Then, state the type of transformation.
::然后,说说变换的类型。

Reflection
::反射反射

The answer is that the change is the result of a reflection.
::答案是,这一变化是反思的结果。

Example 4
::例4

Determine if the change is the result of a translation, reflection or rotation.
::确定更改是翻译、反思或轮换的结果。

After a transformation, the vertices (-3, 6), (-2, 3), (2, 3), (3, 6) become (-3, -1), (-2, 8), (2, 8), (3, 11).
::变换后,顶点(-3、6)、(2、3)、2、3、3、6)变成(-3、3、1、2、8、2、8)、3、11。

First, look at the coordinates to see which coordinate changes.
::首先,看看坐标,看哪个坐标能协调变化。

The $\begin{aligned} x - \end{aligned}$ coordinates stay the same and the $\begin{aligned} y - \end{aligned}$ coordinates change for each of the points.
::x- 坐标保持不变, y- 坐标对每个点都有变化。

Next, determine the type of change for the coordinates.
::下一步,确定坐标的更改类型。

The new $\begin{aligned} y - \end{aligned}$ coordinates are each 5 more than the original coordinates.
::新的Y座标比原来的座标多5个

Then, state the type of transformation.
::然后,说说变换的类型。

Translation
::笔译笔译

The answer is that the change is the result of a translation.
::答案是,修改是翻译的结果。

Example 5
::例5

The points (1, 2), (3, 7), (3, 4), (5, 6) are reflected over the $\begin{aligned} y - \end{aligned}$ axis. What are the new coordinates?
::这些点(1、2)、3、7、3、4、5、6)反映在y-轴上。新的坐标是什么?

First, remember the changes that occur with a reflection over the $\begin{aligned} y - \end{aligned}$ axis.
::首先,请记住随着 Y - 轴反射而发生的变化。

The $\begin{aligned} x - \end{aligned}$ coordinates become the opposite and the $\begin{aligned} y - \end{aligned}$ coordinates stay the same.
::x坐标相反,Y坐标保持不变。

Then, write the new coordinates.
::然后写下新的坐标

(-1, 2), (-3, 7), (-3, 4), (-5, 6)

The answer is that the new coordinates are (-1, 2), (-3, 7), (-3, 4), (-5, 6).
::答案是,新的坐标是(1、2),(3),(7),(3),(4),(5),(6),(1),(2),(3),(7),(3),(4),(5),(6)。

True or false. When there is a reflection in the $\begin{aligned} y - \end{aligned}$ axis, both coordinates change to opposites.
::当 Y - 轴反射时, 两个坐标都向相反方向变化。

Review
::回顾

Use this figure to answer each question. Be sure to write everything in coordinate notation when possible.
::使用此数字回答每个问题。请在可能时将所有信息都写在协调符号中。

Translate this figure three units up.
::把这个数字翻译为3个单位。

Translate this figure four units to the right.
::将这个数字向右翻4个单位。

Translate this figure five units down.
::翻译这个数字 5个单位下来。

Translate this figure six units to the left.
::将这个图向左翻6个单位。

Translate this figure one unit down and two units to the right.
::将图中的一个单位向下和两个单位向右翻转。

Translate this figure two units up and one unit to the left.
::将图中的数字翻译为两个单位向上,一个单位向左。

Translate this figure three units up and one unit to the right.
::将图中的三个单位向上,一个单位向右。

Rotate this figure $\begin{aligned} 180 \end{aligned}$ degrees.
::旋转此图180度。

Rotate this figure $\begin{aligned} 90 \end{aligned}$ degrees counterclockwise.
::逆时针旋转此图 90 度。

Reflect this figure over the $\begin{aligned} x \end{aligned}$ axis.
::在 x 轴上反射此图。

Reflect this figure over the $\begin{aligned} y \end{aligned}$ axis.
::在 y 轴上反射此图。

Translate this figure five units up and three units to the right.
::向右翻5个单位向上和3个单位向上。

Translate this figure six units down and four units to the left.
::将图解为6个单位向下,4个单位向左。

True or false. The figure below is an image of a reflection.
::下图是反射图像。

True or false. This figure has been rotated $\begin{aligned} 180^{\circ} \end{aligned}$ .
::数字是180++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

Section outline

General

翻译、轮换和反思

Finding Coordinates for Translations, Rotations, and Reflections ::翻译、轮换和反省查找坐标

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Finding Coordinates for Translations, Rotations, and Reflections
::翻译、轮换和反省查找坐标

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源