6.9 确定多边形

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 识别多边形

  Collapse Expand

  识别多边形

  

  播放段落

  Dylan is exploring the geodesic dome. He’s figured out that the average dome has in it. These triangles, like all triangles, have a sum of 180° for angle measures. Now, Dylan wants to construct a geodesic dome.
  ::迪伦正在探索大地测量圆顶。他已经发现平均圆顶在其中。 这些三角形和所有三角形一样,都有180度的角度测量量。 现在,迪伦想要建造一个大地测量圆顶。

  播放段落

  As he begins to draw his design, he figures out that he will need a variety of hexagons and pentagons. Dylan is stuck. He can’t figure out how many degrees there will be in each hexagon and how many degrees there will be in each pentagon .
  ::当他开始绘制设计图时,他发现他需要各种各样的六边形和五边形。 迪伦卡住了。 他不知道每个六边形有多少度,每个五边形有多少度。

  播放段落

  In this concept, you will learn to identify polygons.
  ::在这个概念中,你会学会识别多边形。

  播放段落

  Polygons
  ::多边形

  播放段落

  A polygon is a two-dimensional closed figure that has three or more straight sides. Any figure with straight edges, such as a triangle or rectangle , is a polygon. Figures that have any curved sides or open sides are not classed as polygons.
  ::多边形是一个二维封闭的图形,有三面或三面以上。任何有直边缘的图形,如三角形或矩形,都是多边形。凡有弯曲边或开边的数字,均不归类为多边形。

  播放段落

  The following figure is NOT a polygon.
  ::下图不是多边形。

  

  播放段落

  Polygons have special properties that determine their angle and side relationships. For instance, the number of sides a polygon has is related to the number of angles it has, and therefore determines the sum of its angles.
  ::多边形具有决定其角度和侧边关系的特殊属性。例如,多边形的边数与其具有的角度数相关,因此决定其角度的和。

  播放段落

  Now that we can distinguish polygons from other figures, let’s take a closer look at them. In general, there are two kinds of polygons: regular polygons and irregular polygons.
  ::现在,我们可以将多边形与其他数字区分开来,让我们仔细看看它们。 一般来说,有两种多边形:常规多边形和非常规多边形。

  播放段落

  Regular polygon s have sides and angles that are all congruent . If a regular polygon has five congruent sides then it also has five congruent angles. The number of sides of a regular polygon equals the number of interior angles . As long as the sides are congruent and the angles are congruent, the figure is a regular polygon.
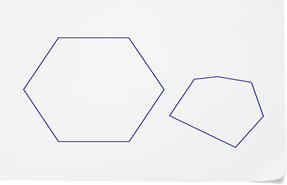
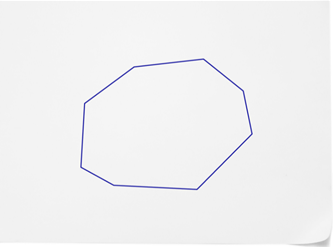
  ::常规多边形的侧面和角度都是相同的。如果正则多边形的侧面有5个相近的侧面,那么它也有5个相近的角。正则多边形的侧面数等于内部角度数。只要两边是相近的,而角度是相近的,数字就是一个正则多边形。

  播放段落

  Irregular polygons are polygons that do NOT have congruent sides and angles. They are still polygons because they have straight, closed sides. The sides of irregular polygons are different lengths. The following diagram shows a regular and an irregular polygon .
  ::非正统多边形是多边形,没有相似的边和角。它们仍然是多边形,因为它们有直的、封闭的边。非正统多边形的两边长度不同。下图显示一个正反多边形。

  

  播放段落

  Each polygon shown in the diagram has six sides and six interior angles. Both of the polygons are hexagons. The first hexagon has side sides that are equal in length and six interior angles that are equal in measure . This is a regular hexagon. The second hexagon has six sides that are all different lengths and six interior angles that are different measures. This is an irregular hexagon.
  ::图表中显示的每个多边形都有六面和六个内部角度。 多边形都是六边形。 第一个六边形的侧面长度相等, 六个内部角度大小相等。 这是一个普通的六边形。 第二个六边形有六个不同长度的侧面和六个不同计量的内角。 这是一个不规则的六边形。

  播放段落

  Polygons are named according to the number of straight, closed sides. The number of sides and the number of congruent interior angles are the same number. The number of diagonals of an $\begin{array}{r}n\end{array}$ -sided polygon can be found using the formula:
  ::多边形是根据直线、 封闭的边数命名的。 边数和相近的内部角数相同。 使用公式可以找到正向多边形的对角数 :

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=[n(n-3)]÷2\end{array}$$

  
  ::# diagonal=[n-3]# # # diagonal=[n- 3] @% 2

  播放段落

  The sum of the measures of the interior angles of a polygon are different for each polygon. The sum of the interior angles of an $\begin{array}{r}n\end{array}$ -sided polygon can be found using the formula:
  ::多边形内角的测量总和对每个多边形的不同。使用公式,可以找到正面多边形内角的总和:

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(n-2)\end{array}$$

  
  ::内侧角总和=180(n-2)

  播放段落

  Let’s apply these formulas to the following hexagon to determine the number of diagonals and the sum of its interior angles.
  ::让我们将这些公式应用于以下六边形,以确定对角数及其内角之和。

  

  播放段落

  The hexagon is an $\begin{array}{r}n\end{array}$ -sided polygon such that the value of ‘ $\begin{array}{r}n\end{array}$ ’ is 6. The diagonals of a polygon are line segments from one corner to another non-adjacent corner.
  ::六边形是一个正面多边形,因此`n ' 值为6。 多边形的对角是从一个角到另一个非邻接角的线条段。

  播放段落

  The number of diagonals can be calculated using the formula:
  ::可使用公式计算对角数数:

  播放段落

  $$\begin{array}{r}\begin{array}{rcl}\mathrm{\#}\text{of diagonals}& =& [n(n-3)]÷2\text{Where}n=6.\\ \mathrm{\#}\text{of diagonals}& =& [6(6-3)]÷2\text{Substitute}6\text{for}n\\ \mathrm{\#}\text{of diagonals}& =& [6(3)]÷2\text{Perform the subtraction inside the parenthesis}\\ \mathrm{\#}\text{of diagonals}& =& 18÷2\text{Perform the multiplication inside the square brackets}\\ \mathrm{\#}\text{of diagonals}& =& 9\text{Perform the division.}\end{array}\end{array}$$

  
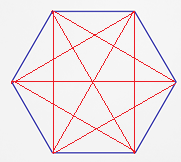
  ::# diagonals = [n(n- 3)]\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\dddddddddd\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  The following diagram shows the nine diagonals of the hexagon.
  ::下图显示了六边形的九对角。

  

  播放段落

  The sum of the interior angles of an $\begin{array}{r}n\end{array}$ -sided polygon can be calculated using the formula:
  ::n侧边多边形的内部角之和,可以用下列公式计算:

  播放段落

  $\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(n-2)\end{array}$ . Where ‘ $\begin{array}{r}n\end{array}$ ’ is the number of sides of the polygon.
  ::内角总和=180(n-2),其中`n ' 是多边形的边数。

  播放段落

  The number of triangles formed by the diagonals of an $\begin{array}{r}n\end{array}$ -sided polygon is  $\begin{array}{r}(n-2)\end{array}$ or two less than the number of sides. Remember, the sum of the interior angles of a triangle is 180°.
  ::由正向多边形对角形成的三角数(n-2) 或小于边数的两边。 记住, 三角形内部角的总和为 180 度。

  播放段落

  $$\begin{array}{r}\begin{array}{rcl}\text{Sum of interior angles}& =& {180}^{\circ }(n-2)\text{Where the value of}n\text{for a hexagon is}6.\\ \text{Sum of interior angles}& =& {180}^{\circ }(6-2)\text{Perform the subtraction inside the parenthesis.}\\ \text{Sum of interior angles}& =& {180}^{\circ }(4)\text{Perform the multiplication}\\ \text{Sum of interior angles}& =& {720}^{\circ }\end{array}\end{array}$$

  
  ::六边形的 n 值为 6.Sm 内角= 180 {( 6-2) 在括号内执行减法。

  播放段落

  The simplest way to record the properties of the various regular polygons is by using a table.
  ::记录各种正多边形属性的最简单方式是使用表格。

  Name of Polygon	Polygon	# of sides	# of angles	播放段落 # of diagonals ::的对角音 # 播放段落 $\begin{array}{r}n(n-3)÷2\end{array}$ ::n-3,%2	播放段落 Sum of angles ::角度和 播放段落 $\begin{array}{r}{180}^{\circ }(n-2)\end{array}$ ::180(n-2)
  Triangle		Tri 3	3	0	180°
  Square/Rectangle		4	4	2	360°
  Pentagon		Penta 5	5	5	540°
  Hexagon		Hexa 6	6	9	720°
  Heptagon		Hepta 7	7	14	900°
  Octagon		Octa 8	8	20	1080°
  Nonagon		Nona 9	9	27	1260°
  Decagon		Deca 10	10	35	1440°

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about Dylan and his geodesic dome. He needs to figure out the sum of the interior angles for both a pentagon and a hexagon.
  ::早些时候,有人给了你Dylan和他的大地测量圆顶的问题。他需要找出五角形和六角形的内部角度的总和。

  播放段落

  Dylan can use the formula:
  ::迪伦可以使用公式:

  播放段落

  $$\begin{array}{r}\begin{array}{rcl}\text{Sum of interior angles}& =& {180}^{\circ }(n-2)\\ \text{Sum of interior angles}& =& {180}^{\circ }(n-2)\text{Where the value of}n\text{for a pentagon is}5.\\ \text{Sum of interior angles}& =& {180}^{\circ }(5-2)\text{Perform the subtraction inside the parenthesis}.\\ \text{Sum of interior angles}& =& {180}^{\circ }(3)\text{Perform the multiplication}\\ \text{Sum of interior angles}& =& {540}^{\circ }\end{array}\end{array}$$

  
  ::内角=180(n-2)-Sum 内角=180(n-2)-Sum 内角=180(n-2)-2,其中内角的 n值为5.Sum 内角=180(5-2) 执行括号内减法。内角的 Sum 内角=180(3) 将内角的倍增Sum=540

  播放段落

  $$\begin{array}{r}\begin{array}{rcl}\text{Sum of interior angles}& =& {180}^{\circ }(n-2)\text{Where the value of}n\text{for a hexagon is}6.\\ \text{Sum of interior angles}& =& {180}^{\circ }(6-2)\text{Perform the subtraction inside the parenthesis}.\\ \text{Sum of interior angles}& =& {180}^{\circ }(4)\text{Perform the multiplication}\\ \text{Sum of interior angles}& =& {720}^{\circ }\end{array}\end{array}$$

  
  ::六边形的 n 值为 6.Sm 内角= 180 {( 6-2) 在括号内执行减法。

  播放段落

  Dylan will figure out that the sum of the interior angles of a pentagon is 540° and the sum of the interior angles of a hexagon is 720°.
  ::迪伦会发现,五角形的内部角总和为540°,六角形的内部角总和为720°。

  播放段落

  Example 2
  ::例2

  播放段落

  What is the measure of each interior angle in a regular octagon?
  ::普通八边形中每个内角的量度是多少?

  播放段落

  First, write the formula to calculate the sum of the interior angles of an octagon.
  ::首先,写出计算八边形内角总和的公式。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(n-2)\end{array}$$

  
  ::内侧角总和=180(n-2)

  播放段落

  Next, substitute 8 for the value of $\begin{array}{r}n\end{array}$ .
  ::下一位, 替换 N 值的 8 。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(8-2)\end{array}$$

  
  ::内角角总和=180( 8-2)

  播放段落

  Next, perform the subtraction inside the parenthesis.
  ::下一步,在括号内执行减法。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(6)\end{array}$$

  
  ::内角总和=180(6)

  播放段落

  Then, perform the multiplication.
  ::然后,执行乘法。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={1080}^{\circ }\end{array}$$

  
  ::内角总和=1080 {_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  The answer is 1080.
  ::答案是1080

  播放段落

  The sum of the 8 interior angles is 1080°.
  ::8个内部角度的总和是1080度。

  播放段落

  The interior angles of a regular octagon are congruent. The measure of each interior angle can be calculate by dividing the sum of the interior angles by the number of angles.
  ::正则八边形的内部角是相似的。每个内部角的度量可以通过将内部角的和和除以角度数来计算。

  $$\begin{array}{r}\frac{{1080}^{\circ }}{8}={135}^{\circ }\end{array}$$

  播放段落

  Example 3
  ::例3

  播放段落

  How many diagonals can be drawn in a regular nonagon?
  ::在普通的非对角中可以绘制多少对角线 ?

  播放段落

  First, write the formula for calculating the number of diagonals for an $\begin{array}{r}n\end{array}$ -sided polygon.
  ::首先,写出计算正向多边形对角数的公式。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonals}=[n(n-3)]÷2\text{Where}n=9\text{for a nonagon}\end{array}$$

  
  ::对角线 # # = [n(n- 3)]\\\\\\\\\\\\\\\\\\ n=9 中的非角的 n=9\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Next, substitute 9 for  $\begin{array}{r}n\end{array}$ in the formula.
  ::接下来,在公式中, n 替换 9 。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=[9(9-3)]÷2\end{array}$$

  
  ::# diagonal=[9(9- 3)] @% 2

  播放段落

  Next, perform the subtraction inside the parenthesis.
  ::下一步,在括号内执行减法。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=[9(6)]÷2\end{array}$$

  
  ::# 的对角线=[9(6)] @%2

  播放段落

  Next, perform the multiplication inside the square brackets.
  ::下一步,在方括号内执行乘法。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonals}=54÷2\end{array}$$

  
  ::# 在对角线=54#2中 #

  播放段落

  Then, perform the indicate division.
  ::然后,执行指示的划分。

  播放段落

   

  $$\begin{array}{r}\mathrm{\#}\text{of diagonals}=27\end{array}$$

  
  ::在对角线=27中#

  播放段落

  The answer is 27.
  ::答案是27个

  播放段落

  Twenty-seven diagonals can be drawn in a regular nonagon.
  ::27个对角体可以用普通的非角画成。

  播放段落

  Example 4
  ::例4

  播放段落

  If a dodecagon is a regular polygon with 12 sides, what is the sum of the interior angles?
  ::如果十二角是12边的正多边形,内角的总和是多少?

  播放段落

  First, write the formula to calculate the sum of the interior angles of a dodecagon.
  ::首先,写入公式以计算十二进制的内角之和。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(n-2)\end{array}$$

  
  ::内侧角总和=180(n-2)

  播放段落

  Next, substitute 12 for the value of $\begin{array}{r}n\end{array}$ .
  ::下一步,以 12 代替 n 的值。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(12-2)\end{array}$$

  
  ::内侧角总和=180(( 12-2)- 2)

  播放段落

  Next, perform the subtraction inside the parenthesis.
  ::下一步,在括号内执行减法。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={180}^{\circ }(10)\end{array}$$

  
  ::内侧角总和=180 (10)

  播放段落

  Then, perform the multiplication.
  ::然后,执行乘法。

  播放段落

  $$\begin{array}{r}\text{Sum of interior angles}={1800}^{\circ }\end{array}$$

  
  ::内侧角总和=1800 {____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  The answer is 1800.
  ::答案是1800

  播放段落

  The sum of the 12 interior angles is 1800°.
  ::12个内部角度的总和是1800°。

  播放段落

  Example 5
  ::例5

  播放段落

  If an icosagon is a regular polygon with 20 sides, what is the number of diagonals that can be drawn inside this polygon?
  ::如果一个象形是具有20边的正多边形,在这个多边形内可以绘制的对角数是多少?

  播放段落

  First, write the formula for calculating the number of diagonals for an $\begin{array}{r}n\end{array}$ -sided polygon.
  ::首先,写出计算正向多边形对角数的公式。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=[n(n-3)]÷2\text{Where}n=20\text{for an icosagon}\end{array}$$

  
  ::# diagonal = [n(n- 3)]\\\\\\\\\\\\\\\\\\ n=20 对于象形

  播放段落

  Next, substitute 20 for  $\begin{array}{r}n\end{array}$ in the formula.
  ::下一个,在公式中以n代替20。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=[20(20-3)]÷2\end{array}$$

  
  ::# diagonal=[20(20) -3)] @% 2

  播放段落

  Next, perform the subtraction inside the parenthesis.
  ::下一步,在括号内执行减法。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=[20(17)]÷2\end{array}$$

  
  ::# 的对角线=[20(17)] @ @%2

  播放段落

  Next, perform the multiplication inside the square brackets.
  ::下一步,在方括号内执行乘法。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=340÷2\end{array}$$

  
  ::# 的对角线=340 # 2

  播放段落

  Then, perform the indicate division.
  ::然后,执行指示的划分。

  播放段落

  $$\begin{array}{r}\mathrm{\#}\text{of diagonal}=170\end{array}$$

  
  ::对角线=170 #

  播放段落

  The answer is 170.
  ::答案是170

  播放段落

  One hundred and seventy diagonals can be drawn in a regular icosagon.
  ::在普通的象牙形中可以画出一百七十个对角体。

  播放段落

  Review
  ::回顾

  播放段落

  Answer true or false to each question about regular and irregular polygons.
  ::对每个关于常规和非常规多边形的问题都回答正确或错误。

  播放段落

  1. The angles of a regular polygon are all the same size.
  ::1. 普通多边形的角度均相同。

  播放段落

  2. A regular hexagon has six sides that are different lengths.
  ::2. 普通六边形的六边长度不同。

  播放段落

  3. An irregular pentagon has sides that are the same length.
  ::3. 非正常的五边形具有相同长度的一面。

  播放段落

  4. An irregular polygon is one that has one side open.
  ::4. 非正常多边形是一面开放的多边形。

  播放段落

  5. A regular triangle could also be called an equilateral triangle.
  ::5. 正常三角也可以称为等边三角。

  播放段落

  6. The side lengths of a regular octagon are all the same length.
  ::6. 普通八边形的侧边长度相同。

  播放段落

  Identify each figure as regular or irregular. Then identify the type of polygon that it is too.
  ::确定每个数字为常规或非常规。 然后确定它也是哪类多边形 。

  7.

  

  播放段落

  8. An eight sided figure with sides of equal length.
  ::8. 8个侧面数字,两侧长度相等。

  9. 

  

  10.

  

  11. 

  

  播放段落

  Use the formula  $\begin{array}{r}(n-2)\times 180\end{array}$ to figure out the sum of the angle measures of each polygon.
  ::使用公式(n-2)x180 来计算每个多边形角量度的总和。

  播放段落

  12. Regular hexagon
  ::12. 普通六边形

  播放段落

  13. Regular octagon
  ::13. 普通八边

  播放段落

  14. Triangle
  ::14. 三角形

  播放段落

  15. Trapezoid
  ::15. 记录片

  播放段落

  16. Decagon
  ::16. 十角

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。