6.16 识别发射物

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 识别信号

  Collapse Expand

  识别信号

  

  播放段落

  A honeycomb is said to have regular tessellations. Looking at this image, can you identify what it means to tessellate?
  ::据说蜂窝经常有星系变异。看看这个图像,你能辨别它意味着什么吗?

  播放段落

  In this concept, you will learn to identify tessellations.
  ::在这一概念中,你将学会辨别星系。

  播放段落

  Tessellations
  ::发射

  播放段落

  You can use translations and reflections to make patterns with geometric figures called tessellations . A tessellation is a pattern in which geometric figures repeat without any gaps between them. In other words, the repeated figures fit perfectly together. They form a pattern that can stretch in every direction on the coordinate plane .
  ::您可以使用翻译和反射来用几何数字来制作图案,称为星系通缩。 星系通缩是一种图案, 几何数字重复, 彼此间没有任何差距。 换句话说, 重复的数字完全吻合。 它们形成一个图案, 可以在坐标平面的每个方向延伸 。

  播放段落

  Take a look at the tessellations below. The tessellation can go on and on forever.
  ::看看下面的星系 星系会一直延续下去

  

  播放段落

  You can create tessellations by moving a single geometric figure. You can perform transformations such as translations and rotations to move the figure so that the original and the new figure fit together.
  ::您可以通过移动单个几何图创建星系。您可以进行翻译和旋转等转换,以移动数字,使原始和新数字相容。

  播放段落

  How do you know that a figure will tessellate?
  ::你怎么知道一个数字会变色?

  播放段落

  If the figure is the same on all sides, it will fit together when it is repeated. Figures that tessellate tend to be regular polygons. Regular polygons have congruent straight sides. When you rotate or slide a regular polygon , the side of the original figure and the side of its translation will match. Not all geometric figures can tessellate. When you translate or rotate them, their sides do not fit together.
  ::如果数字在所有边上都相同, 当重复时它会合在一起。 数字的板块往往是普通多边形。 普通多边形有相近的正直边。 当您旋转或滑动一个正多边形时, 原始图的侧面及其翻译的侧面会匹配。 并非所有几何数字都能相互叠加。 当您翻译或旋转时, 它们的侧面不相容 。

  播放段落

  Remember this rule and you will know whether a figure will tessellate or not! Think about whether or not there will be gaps in the pattern as you move a figure.
  ::记住此规则, 您就会知道数字是否会变形 ! 想想在移动数字时该图案是否会出现空白 。

  播放段落

  Take a look at this situation.
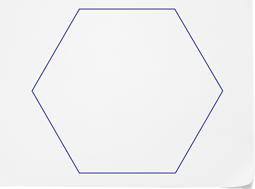
  ::看看这个情况。

  播放段落

  Create a tessellation by repeating the following figure.
  ::通过重复下图创建套索。

  

  播放段落

  First, trace the figure on a piece of stiff paper and then cut it out. This will let you perform translations easily so you can see how best to repeat the figure to make a tessellation.
  ::首先, 追踪一张硬纸上的图, 然后剪掉它 。 这样您就可以轻松地进行翻译, 这样您就可以看到如何最好地重复这个图, 来做熔化 。

  播放段落

  This figure is exactly the same on all sides, so you do not need to rotate it to make the pieces fit together. Instead, let’s try translating it.
  ::这个数字在所有方面都完全一样,所以你不需要旋转它来使碎片合在一起。 相反,让我们试着翻译它。

  播放段落

  Next, trace the figure. Then slide the cutout so that one edge of it lines up perfectly with one edge of the figure you drew. Trace the cutout again.
  ::接下来,追踪图案。然后滑动剪切图,这样它的一个边缘与你绘制的图的边缘一齐。再次追踪剪切图。

  播放段落

  Then, line the cutout up with another side of the original figure and trace it. As you add figures to the pattern, the hexagons will start making themselves!
  ::然后用原始图象的另一面排出剪切线并追踪它。当你在图案中添加数字时,六边形将开始自我生成!

  播放段落

  Check to make sure that there are no gaps in your pattern. All of the edges should fit perfectly together. You should be able to continue sliding and tracing the hexagon forever in all directions. You have made a tessellation!
  ::选中此选项可以确保您的图案没有空白 。 所有边缘都应该完全相容 。 您应该能够继续滑动, 并在所有方向永久跟踪六边形 。 您已经做了熔化 !

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about  tessellating honeycomb.
  ::早些时候,有人给你一个问题 沟通蜂窝。

  播放段落

  To tessellate means that congruent figures are put together to create a pattern where there aren’t any gaps or spaces in the pattern. Figures can be put side by side and/or upside down to create the pattern. The pattern is called a tessellation. If you look at the honeycomb, you can see that hexagons are tessellating.
  ::tesellate 意味着将相匹配的数字组合在一起, 以形成一种模式, 从而在模式中不存在任何空白或空格。 数字可以并排和/ 或倒着排列, 以创建模式。 模式被称为通缩。 如果您查看蜂窝, 您可以看到六边形是交汇的 。

  播放段落

  Regular polygons will tessellate as long as one of their interior angles is a factor of 360°. To find the interior angles of a regular polygon, you use the formula: 
  ::普通多边形的内角为360°的系数时,正方形的内角会系星体。要找到正方形的内角,请使用公式:

  播放段落

  $$\begin{array}{r}\frac{180(n-2)}{n}\end{array}$$

  
  ::180(n-2)n

  播放段落

  where $\begin{array}{r}n\end{array}$  is the number of sides in the polygon .
  ::其中 n 是多边形的边数。

  播放段落

  One interior angle of a regular pentagon (5 sides) is $\begin{array}{r}\frac{180(5-2)}{5}=\frac{540}{5}-{108}^{\circ }\end{array}$ . 360° is not divisible by 108°. $\begin{array}{r}\frac{360}{108}=3.333\end{array}$ . Because 108 is not a factor of 360, a regular pentagon will not tessellate.
  ::普通五角形的内角(5面)为180(5-2)5=5405-108.360°不能除以108°.360108=3.333.由于108不是360系数,普通五角形不会延展。

  播放段落

  A regular hexagon (like in the honeycomb) does tessellate. One interior angle of a regular hexagon is $\begin{array}{r}\frac{180(6-2)}{6}=\frac{720}{6}={120}^{\circ }\end{array}$ . 360° is divisible by 120°. $\begin{array}{r}\frac{360}{120}=3\end{array}$ . Because 120 is a factor of 360, a regular hexagon will tessellate.
  ::普通六边形(如蜂窝中)比方为。普通六边形的内角为180(6-2)6=7206=120。360°可除以120°.360120=3。由于120是360的系数,普通六边形的内角将变贝。

  播放段落

  Example 2
  ::例2

  播放段落

  Draw a tessellation of .
  ::绘制 .

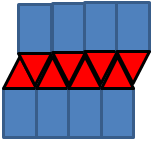
  播放段落

  In an equilateral triangle each angle is 60°. Therefore, six triangles will perfectly fit around each point to make a hexagon.
  ::在等边三角形中,每个角为60度。因此,6个三角形将完全适合在每个点周围形成六边形。

  

  播放段落

  Example 3
  ::例3

  播放段落

  Does this figure tessellate? Why or why not?
  ::这张图是石板吗 为什么或者为什么?

  

  播放段落

  First, look at the image. Notice that it is a right triangle . Two right triangles will fit together to make a square .
  ::首先,看看图像。 注意它是一个右三角形。 两个右三角形将合在一起组成方形 。

  播放段落

  Next, see if the right triangles will fit together with no gaps.
  ::接下来,看看正确的三角形是否合合,没有缺口。

  

  播放段落

  The answer is yes, the right triangle will tessellate.
  ::答案是肯定的 正确的三角形会变形

  播放段落

  Example 4
  ::例4

  播放段落

  Does this figure tessellate? Why or why not?
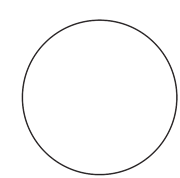
  ::这张图是石板吗 为什么或者为什么?

  

  播放段落

  First, look at the image. It is a circle .
  ::首先,看看图像,这是一个圆圈。

  播放段落

  Next, see if the circles will fit together with no gaps.
  ::接下来,看看圆圈是否合而为一,没有漏洞。

  

  播放段落

  The answer is no, circles will not tessellate. Notice that there are gaps in the diagram .
  ::答案是否,圆圈不会变形,注意图中存在空白。

  播放段落

  Example 5
  ::例5

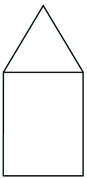
  播放段落

  Does this figure tessellate? Why or why not?
  ::这张图是石板吗 为什么或者为什么?

  

  播放段落

  First, look at the image. Notice that it is a rectangle with an equilateral triangle on top. Equilateral triangles do tessellate as do .
  ::首先, 看看图像。 注意它是一个与顶部的等边三角形的矩形 。 等边三角形同样会使用 etsellate 。

  播放段落

  Next, see if the figure will fit together with no gaps.
  ::接下来,看看这个数字是否与时俱进,没有差距。

  

  播放段落

  The answer is yes, the figures will tessellate because it is made up of two shapes that do tessellate.
  ::答案是肯定的 数字会变贝化 因为它由两种形状组成 两种形状可以变贝化

  播放段落

  Review
  ::回顾

  播放段落

  Will the following figures tessellate?
  ::下述数字会变贝质吗?

  播放段落
  1. A regular pentagon
     ::经常的五角形
  播放段落
  2. A regular octagon
     ::一个正正正八边
  播放段落
  3. A square
     ::一个平方
  播放段落
  4. A rectangle
     ::矩形
  播放段落
  5. An equilateral triangle
     ::等边三角形
  播放段落
  6. A parallelogram
     ::平行图
  播放段落
  7. A circle
     ::一个圆圆
  播放段落
  8. A cylinder
     ::A 圆柱体
  播放段落
  9. A cube
     ::A 立方体
  播放段落
  10. A cone
      ::锥体
  播放段落
  11. A sphere
      ::A领域
  播放段落
  12. A rectangular prism
      ::矩形棱镜
  播放段落
  13. A right triangle
      ::右三角形
  播放段落
  14. A regular heptagon
      ::常规七边形
  播放段落
  15. A regular decagon
      ::一个正正十角

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

   

  播放段落

  Resources
  ::资源