课程： 6.17 承认相似性

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节承认相似性

折叠展开
承认相似性
When walking home from school, Amira walks past a tower that casts a shadow that is 10 feet long. Standing next to it, she notices that she casts a shadow of 2 feet. Amira knows that she is exactly five feet tall. How can she use this information to determine the height of the tower?
::当Amira从学校回家时,Amira走过一个10英尺长的塔,抛出一个10英尺长的阴影。站在塔旁边,她注意到她投了2英尺长的阴影。Amira知道她正好是5英尺高。她如何利用这些信息确定塔的高度?

In this concept, you will learn to recognize similarity.
::在这一概念中,你会学会认识相似性。

Similarity
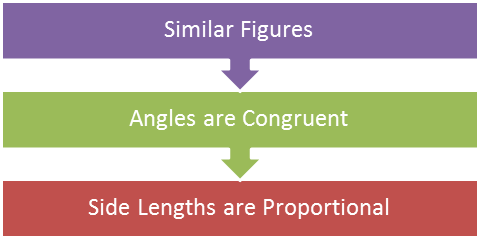
::相似性

Congruent means exactly the same, having the same size and shape.
::共和意指完全一样, 大小和形状都一样。

Sometimes, a figure will have the same shape, but not the same size. It will be either smaller or larger than the original figure. When this happens, you say that the two figures are similar . have the same shape, but not the same size.
::有时, 数字会具有相同的形状, 但大小不同。它会小于或大于原图。发生这种情况时, 您会说这两个数字相似, 形状相同, 但大小不同。

Think about this for a minute, if a figure has the same shape, but not the same size, then there is still a relationship between the two figures. The relationship is created based on the shape being the same.
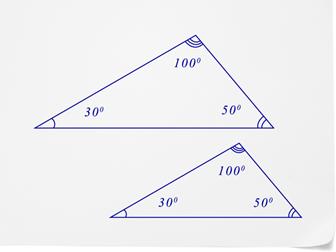
::仔细想一想,如果一个数字的形状相同,但大小不同,那么这两个数字之间还存在某种关系。这种关系是根据相同的形状建立的。

Let’s start by thinking about angles . With similar figures, each angle of one figure in a similar pair corresponds and is congruent to an angle in the other.
::让我们首先思考角度。以相似的数字,一个数字的每个角度在相似的一对中对应,并且与另一个角度一致。

For instance, the top point of one triangle corresponds to the top point of the other triangle in a similar pair. You call these corresponding parts.
::例如,一个三角形的顶点对应另一个三角形的顶点,在相似的一对中。您将这些相应部分称为相应部分。

Notice that the angles in the triangles above match in these two triangles. The shape of the triangles is the same, and you can see that the angles do match.
::注意上方三角形中的角度与这两个三角形中的角度匹配。三角形的形状相同, 您可以看到角是匹配的。

Now, let’s look at side lengths. The sides in similar pairs also correspond to each other (such as the base of each triangle), but they are not congruent; they are proportional. You can determine whether figures are similar to each other by comparing their corresponding parts. Corresponding parts are especially helpful when one figure is rotated so that it is not clear which angles and sides correspond to which in the other figure.
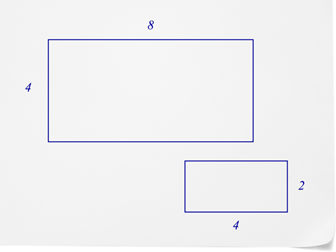
::现在,让我们来看看侧边长度。相近对对面的两边彼此对应( 如每三角的底部) , 但它们不相容; 它们是比例的。您可以通过比较相应的部分来确定数字是否相近。当一个数字旋转时,对应部分特别有用,因此不清楚另一个数字中哪个角度和边对应哪个角度和边对应哪个方向。

Look at the image below of the two .
::看看这两张照片的下方。

Let’s look at the corresponding side lengths.
::让我们看看相应的侧边长度。

In the first rectangle , the short side is 4 and the long side is 8. You know that opposite sides of a rectangle are congruent, so you don’t need to worry about writing measurements on the other two sides.
::在第一个矩形中,短边是4,长边是8。你知道矩形的对面是相似的, 所以你不必担心写其他两边的测量。

In the second rectangle, the short side is 2 and the long side is 4.
::在第二个矩形中,短边是2,长边是4。

You can compare the measurements in the first rectangle with the ones in the second rectangle.
::您可以比较第一个矩形的测量和第二个矩形的测量。

First, let’s write a proportion to compare the corresponding sides .
::首先,让我们写一个比例来比较对应的两面。

$\begin{aligned} \begin{array}{rcl} \frac{short side}{short side} & = & \frac{long side}{long side} \\ \frac{4}{2} & = & \frac{8}{4} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{\text{short side}}{\text{short side}} &=& \frac{\text{long side}}{\text{long side}} \\ \frac{4}{2} &=& \frac{8}{4} \end{array}\end{align*}$
::短侧侧靠侧=长侧侧42=84

Next, you can see that these two ratios form a proportion. You can use this information to prove whether or not two figures are similar as well. Remember, the angle measures must be the same, and the side lengths must be proportional.
::接下来,您可以看到这两个比例构成一个比例。您可以使用此信息来证明两个数字是否相似。记住, 角度量度必须是相同的, 边长必须是比例的。

$\begin{aligned} \begin{array}{rcl} \frac{4}{2} & = & \frac{8}{4} \\ 2 & = & 2 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{4}{2} &=& \frac{8}{4} \\ 2 &=& 2 \end{array}\end{align*}$

The answer is that the two rectangles are similar since the angles are congruent (all 90°) and the side lengths are proportional.
::答案是,这两个矩形是相似的,因为角是相同的(全部90度),侧长是成比例的。

Now that you understand how to identify whether or not two figures are similar, we will look at similar triangles . Similar triangles are very useful because you can use them to figure out measurements.
::既然您了解了如何确定两个数字是否相似, 我们将查看相似的三角形。相似的三角形非常有用, 因为您可以使用它们来计算测量。

Many years ago, this is how people used to figure out the measurements for things that were too high or big to measure . They used . Indirect measurement uses similar triangles and proportions to figure out lengths or distances.
::许多年前,人们就用这个方法来计算那些太高或太大无法测量的东西。他们使用过。间接测量使用类似的三角形和比例来计算长度或距离。

First, let’s think about similar triangles.
::首先,让我们想想类似的三角形。

Similar triangles have the same properties as other similar figures. The angle measures are the same and the corresponding side lengths are proportional.
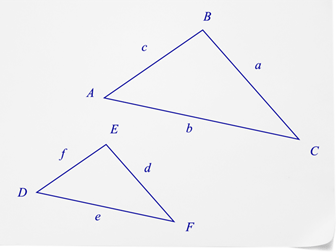
::类似三角形的属性与其他类似数字相同。角度量度相同,相应的侧边长度成比例。

Let’s look at this diagram to understand this.
::让我们看看这个图表来理解这一点。

First, let’s compare the angle measures.
::首先,让我们比较角度计量。

$\begin{aligned} \begin{array}{rcl} ∠ A & ≅ & ∠ D \\ ∠ B & ≅ & ∠ E \\ ∠ C & ≅ & ∠ F \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \angle A & \cong & \angle D \\ \angle B & \cong & \angle E \\ \angle C & \cong & \angle F \end{array}\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}阿达巴 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}阿达巴 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}阿达巴 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

Next, you can look at the corresponding side lengths. In the diagram, you haven’t been given any measurements, but you can use the lowercase letters to show which sides correspond.
::接下来, 您可以查看相应的侧边长度。在图表中, 您没有得到任何测量, 但是您可以使用小写字母来显示对应的边。

$\begin{aligned} \frac{a}{d} = \frac{b}{e} = \frac{c}{f} \end{aligned}$
$\begin{align*}\frac{a}{d} = \frac{b}{e} = \frac{c}{f}\end{align*}$
::ad=be=参考

This shows that the side lengths form a ratio and that each of these is proportional to the other.
::这表明侧长度形成一个比率,而其中的每一个则与另一个成正比。

You can use this information when problem solving for missing side lengths. First, we would have to know some of the side lengths.
::问题解答时您可以使用此信息。首先, 我们必须知道一些侧边长度。

Let’s assign some lengths to the sides in the diagram above.
::让我们为上图中的两边指定一些长度。

$\begin{align*}\begin{array}{rcl} a &=& 12 \\ b &=& ? \\ c &=& 3 \\ d &=& 4 \\ e &=& 3 \\ f &=& 1 \end{array} \end{align*}$
::a=12b=? c=3d=4e=3f=1

First, you can take these given measures and substitute them into the proportion that you wrote earlier. Notice that you don’t have the measure of side $\begin{align*}b\end{align*}$ , so you will need to solve for that missing measurement.
::首先,你可以采取这些给定的计量方法,并把它们替换成你先前写过的比例。请注意,你没有b的度量,所以你需要解决这一缺失的度量问题。

$\begin{aligned} \begin{array}{rcl} \frac{a}{d} = \frac{b}{e} = \frac{c}{f} \\ \frac{12}{4} = \frac{b}{3} = \frac{3}{1} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} && \frac{a}{d} = \frac{b}{e} = \frac{c}{f} \\ && \frac{12}{4} = \frac{b}{3} = \frac{3}{1} \end{array}\end{align*}$
::ad=be=cf124=b3=31

Next, you can use two of the three ratios to solve the proportions. You have three ratios, but you don’t need all three because two equal ratios form a proportion. This means that you only need to work with two ratios to solve for the value of $\begin{align*}b\end{align*}$ .
::接下来,您可以使用三个比例中的两个来解答比例。您有三个比例, 但是您不需要全部三个比例, 因为两个同等比例形成一个比例。这意味着您只需要用两个比例来解答 b 值, 就需要用两个比例来解答。

$\begin{aligned} \begin{array}{rcl} \frac{a}{d} & = & \frac{b}{e} \\ \frac{12}{4} & = & \frac{b}{3} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{a}{d} &=& \frac{b}{e} \\ \\ \frac{12}{4} &=& \frac{b}{3} \end{array}\end{align*}$
::ad=be124=b3 (ab=b3)

Then, use algebra to solve the proportion.
::然后用代数来解析比例。

$\begin{aligned} \begin{array}{rcl} \frac{12}{4} & = & \frac{b}{3} \\ 4 b & = & 12 \times 3 \\ 4 b & = & 36 \\ \frac{4 b}{4} & = & \frac{36}{4} \\ b & = & 9 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{12}{4} &=& \frac{b}{3} \\ 4 b &=& 12 \times 3 \\ 4 b &=& 36 \\ \frac{4b}{4} &=& \frac{36}{4} \\ b &=& 9 \end{array}\end{align*}$
::124=b34b=12x34b=364b4=364b=9

The answer is 9.
::答案是9。

The value of $\begin{align*}b\end{align*}$ is 9.
::b 值为 9 。

The key to working with indirect measurement is to always be clear about what is being compared. You write the ratios and then form a proportion to solve for the missing length or distance .
::进行间接测量的关键是总是要清楚比较的是什么。您要写出比率, 然后形成一个比例, 以解答缺失的长度或距离。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Amira and her shadows.
::早些时候,你被问及Amira和她的影子。

Notice that the person and the shadow form two sides of a triangle and you can draw an imaginary line from the head of the person to the tip of the shadow. Shadows are a way of working with triangles and indirect measurement. In fact, you will often hear these types of problems referred to as shadow problems.
::请注意, 人和阴影是三角形的两面, 您可以从人的头到阴影的一角画一条假想的线。阴影是三角形和间接测量的一种工作方式。事实上, 您通常会听到被称为影子问题的这类问题。

To solve this one, let’s figure out how to use similar triangles to figure out the height of the tower.
::为了解决这一难题,让我们想一想如何使用类似的三角形来计算塔的高度。

First, think about what is being compared. You are comparing the height of the person, Amira, with the length of the shadow. That is the first ratio.
::首先,先想想比较中比较的是什么。你正在比较一个人的高度,阿米拉,和阴影的长度。这是第一个比例。

$\begin{aligned} \frac{person}{shadow} = \frac{5 f t}{2 f t} \end{aligned}$
$\begin{align*}\frac{\text{person}}{\text{shadow}} = \frac{5 \ ft}{2 \ ft} \end{align*}$
::人均海道=5平方英尺

Next, look at the tower. You don’t know the height of the tower that is our variable. You do know the length of the shadow. Here is the second ratio.
::接下来,请看看塔台。你不知道塔台的高度是我们的变量。你知道阴影的长度。这是第二个比例。

$\begin{aligned} \frac{tower}{shadow} = \frac{x f t}{10 f t} \end{aligned}$
$\begin{align*}\frac{\text{tower}}{\text{shadow}} = \frac{x \ ft}{10 \ ft}\end{align*}$
::塔沙ow=x 平方英尺10平方英尺

Then, you can say that these two triangles are similar and that similar triangles are proportional. Therefore, these two ratios form a proportion. Let’s write them as a proportion.
::然后,你可以说这两个三角形是相似的,而相似的三角形是比例的。因此,这两个比率是一个比例。让我们把它们写成一个比例。

$\begin{aligned} \frac{5 f t}{2 f t} = \frac{x f t}{10 f t} \end{aligned}$
$\begin{align*}\frac{5 \ ft}{2 \ ft} = \frac{x \ ft}{10 \ ft}\end{align*}$
::5平方英尺=x平方英尺10平方英尺

Then, use algebra to solve the proportion.
::然后用代数来解析比例。

$\begin{aligned} \begin{array}{rcl} \frac{5}{2} & = & \frac{x}{10} \\ 2 x & = & 5 \times 10 \\ 2 x & = & 50 \\ \frac{2 x}{2} & = & \frac{50}{2} \\ x & = & 25 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{5}{2} &=& \frac{x}{10} \\ 2x &=& 5 \times 10 \\ 2x &=& 50 \\ \frac{2x}{2} &=& \frac{50}{2} \\ x &=& 25 \end{array}\end{align*}$
::52=x102x=5xxx102x=502x2=502xx=25

The answer is 25.
::答案是25岁

The tower is 25 feet tall.
::这座塔有25英尺高

Example 2
::例2

Solve for the missing variable.
::解决缺少的变量。

First, you can use two of the three ratios to solve for $\begin{align*}x\end{align*}$ .
::首先,您可以使用三个比例中的两个来解答 x 。

$\begin{aligned} \frac{2}{8} = \frac{24}{x} \end{aligned}$
$\begin{align*}\frac{2}{8} = \frac{24}{x}\end{align*}$
::28=24x 28=24x

Next, use algebra to solve the proportion.
::接下来,使用代数来解析比例。

$\begin{aligned} \begin{array}{rcl} \frac{2}{8} & = & \frac{24}{x} \\ 2 x & = & 24 \times 8 \\ 2 x & = & 192 \\ \frac{2 x}{2} & = & \frac{192}{2} \\ x & = & 96 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{2}{8} &=& \frac{24}{x} \\ 2 x &=& 24 \times 8 \\ 2x &=& 192 \\ \frac{2x}{2} &=& \frac{192}{2} \\ x &=& 96 \end{array}\end{align*}$
::28=24x2x=24x82x=1922x2=1922x6

The answer is 96.
::答案是96。

The value of $\begin{align*}x\end{align*}$ is 96.
::x值为96。

Example 3
::例3

Solve for the missing value.
::解决丢失的值。

$\begin{aligned} \frac{2}{3} = \frac{4}{6} = \frac{x}{18} \end{aligned}$
$\begin{align*}\frac{2}{3} = \frac{4}{6} = \frac{x}{18}\end{align*}$
::23=46=x18

First, you can use two of the three ratios to solve for $\begin{align*}x\end{align*}$ .
::首先,您可以使用三个比例中的两个来解答 x 。

$\begin{aligned} \frac{4}{6} = \frac{x}{18} \end{aligned}$
$\begin{align*}\frac{4}{6} = \frac{x}{18}\end{align*}$
::46=x18

Next, use algebra to solve the proportion.
::接下来,使用代数来解析比例。

$\begin{aligned} \begin{array}{rcl} \frac{4}{6} & = & \frac{x}{18} \\ 6 x & = & 4 \times 18 \\ 6 x & = & 72 \\ \frac{6 x}{6} & = & \frac{72}{6} \\ x & = & 12 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{4}{6} &=& \frac{x}{18} \\ 6x &=& 4 \times 18 \\ 6x &=& 72 \\ \frac{6x}{6} &=& \frac{72}{6} \\ x &=& 12 \end{array}\end{align*}$
::46=x186x=4x186x=726x6=726x=12

The answer is 12.
::答案是12岁

The value of $\begin{align*}x\end{align*}$ is 12.
::x 值为 12 。

Example 4
::例4

Solve for the missing value.
::解决丢失的值。

$\begin{aligned} \frac{4}{5} = \frac{12}{15} = \frac{x}{30} \end{aligned}$
$\begin{align*}\frac{4}{5} = \frac{12}{15} = \frac{x}{30}\end{align*}$
::45=1215=x30

First, you can use two of the three ratios to solve for $\begin{align*}x\end{align*}$ .
::首先,您可以使用三个比例中的两个来解答 x 。

$\begin{aligned} \frac{4}{5} = \frac{x}{30} \end{aligned}$
$\begin{align*}\frac{4}{5} = \frac{x}{30}\end{align*}$
::45=x30

Next, use algebra to solve the proportion.
::接下来,使用代数来解析比例。

$\begin{aligned} \begin{array}{rcl} \frac{4}{5} & = & \frac{x}{30} \\ 5 x & = & 4 \times 30 \\ 5 x & = & 120 \\ \frac{5 x}{5} & = & \frac{120}{5} \\ x & = & 24 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{4}{5} &=& \frac{x}{30} \\ 5x &=& 4 \times 30 \\ 5x &=& 120 \\ \frac{5x}{5} &=& \frac{120}{5} \\ x &=& 24 \end{array}\end{align*}$
::45=x305x=4x305x=3305x=1205x5=1205x=24

The answer is 24.
::答案是24个。

The value of $\begin{align*}x\end{align*}$ is 24.
::x 值为 24 。

Example 5
::例5

Solve for the missing value.
::解决丢失的值。

$\begin{aligned} \frac{8}{9} = \frac{16}{x} = \frac{32}{36} \end{aligned}$
$\begin{align*}\frac{8}{9} = \frac{16}{x} = \frac{32}{36}\end{align*}$
::89=16x=3236

First, you can use two of the three ratios to solve for $\begin{align*}x\end{align*}$ .
::首先,您可以使用三个比例中的两个来解答 x 。

$\begin{aligned} \frac{8}{9} = \frac{16}{x} \end{aligned}$
$\begin{align*}\frac{8}{9} = \frac{16}{x}\end{align*}$
::89=16x 89=16x

Next, use algebra to solve the proportion.
::接下来,使用代数来解析比例。

$\begin{aligned} \begin{array}{rcl} \frac{8}{9} & = & \frac{16}{x} \\ 8 x & = & 9 \times 16 \\ 8 x & = & 144 \\ \frac{8 x}{8} & = & \frac{144}{8} \\ x & = & 18 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{8}{9} &=& \frac{16}{x} \\ 8x &=& 9 \times 16 \\ 8x &=& 144 \\ \frac{8x}{8} &=& \frac{144}{8} \\ x &=& 18 \end{array}\end{align*}$
::89=16x8x=9x168x=148x8=1448x8=148x=18

The answer is 18.
::答案是18岁

The value of $\begin{align*}x\end{align*}$ is 18.
::x 值为 18 。

Review
::回顾

Identify whether or not each pair of triangles is similar based on the ratios of their sides.
::查明每一对三角形是否根据其侧翼比率而相似。

1. Triangle $\begin{align*}A\end{align*}$ has side lengths of 2, 4, and 6. Triangle $\begin{align*}B\end{align*}$ has side lengths of 6, 12 and 24. Are these triangles similar?
::1. 三角A的侧长为2、4和6,三角B的侧长为6、12和24,这些三角是否相似?

2. Triangle $\begin{align*}C\end{align*}$ has side lengths of 4, 5, and 10. Triangle $\begin{align*}B\end{align*}$ has side lengths of 2, 2.5 and 5. Are these two triangles similar?
::2. 三角C的侧长为4、5和10。三角B的侧长为2、2.5和5。这两个三角是否相似?

3. Triangle $\begin{align*}D\end{align*}$ has side lengths of 5, 8, and 12. Triangle $\begin{align*}B\end{align*}$ has side lengths of 10, 16 and 24. Are these two triangles similar?
::3. 三角D的侧长为5、8和12。三角B的侧长为10、16和24。这两个三角是否相似?

4. Triangle $\begin{align*}A\end{align*}$ has side lengths of 10, 12, and 14. Triangle $\begin{align*}B\end{align*}$ has side lengths of 5, 7 and 9. Are these two triangles similar?
::4. 三角A的侧长为10、12和14。三角B的侧长为5、7和9。这两个三角是否相似?

5. Triangle $\begin{align*}B\end{align*}$ has side lengths of 8, 14, and 20. Triangle $\begin{align*}C\end{align*}$ has side lengths of 4, 7 and 10. Are these two triangles similar?
::5. 三角B的侧长为8、14和20,三角C的侧长为4、7和10。这两个三角是否相似?

6. Triangle $\begin{align*}E\end{align*}$ has side lengths of 20, 11 and 8. Triangle $\begin{align*}F\end{align*}$ has side lengths of 10, 5.5 and 5. Are these two triangles similar?
::6. E三角的侧长为20、11和8,F三角的侧长为10、5.5和5,这两个三角是否相似?

7. Triangle $\begin{align*}G\end{align*}$ has side lengths of 6, 8 and 12. Triangle $\begin{align*}H\end{align*}$ has side lengths of 18, 24 and 36. Are these two triangles similar?
::7. 三角G的侧长为6、8和12。三角H的侧长为18、24和36。这两个三角是否相似?

8. Triangle $\begin{align*}I\end{align*}$ has side lengths of 8, 12, and 16. Triangle $\begin{align*}J\end{align*}$ has side lengths of 4, 8 and 10. Are these two triangles similar?
::8. 三角一的侧长为8、12和16,三角J的侧长为4、8和10。这两个三角是否相似?

Find the missing length by looking at each series of ratios. The top value represents the side lengths of the first similar triangle. The bottom value represents the side lengths of the second similar triangle.
::通过查看每个比率序列来查找缺失的长度。顶值代表第一个相似三角形的侧长。底值代表第二个相似三角形的侧长。

9. $\begin{align*}\frac{1}{2} = \frac{3}{6} = \frac{9}{x}\end{align*}$
::9. 12=36=9x

10. $\begin{align*}\frac{3}{6} = \frac{6}{12} = \frac{10}{x}\end{align*}$
::10. 36=612=10x

11. $\begin{align*}\frac{4}{2} = \frac{10}{x} = \frac{12}{6}\end{align*}$
::11. 42=10x=126

12. $\begin{align*}\frac{6}{2} = \frac{9}{x} = \frac{12}{6}\end{align*}$
::12. 62=9x=126

13. $\begin{align*}\frac{5}{10} = \frac{10}{20} = \frac{15}{x}\end{align*}$
::13. 510=1020=15x

14. $\begin{align*}\frac{12}{6} = \frac{20}{10} = \frac{15}{x}\end{align*}$
::14. 126=2010=15x

15. $\begin{align*}\frac{16}{x} = \frac{20}{5} = \frac{24}{6}\end{align*}$
::15. 16x=205=246

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

承认相似性

Similarity ::相似性

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Similarity
::相似性

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)