课程： 9.6 使用拦截 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节使用拦截

折叠展开
使用拦截
Mary Ellen has $60 to spend at the craft store and she is very interested in buying either scrapbooks that cost $10 or fashion stickers that cost $5 per package. Before making a purchase, she needs to know how many scrapbooks or how many packages of stickers she can buy with her money. How can Mary Ellen figure this out?
::玛丽·艾伦在手工艺品商店有60美元,她非常有兴趣购买10美元的剪贴纸,或者每包5美元的时装贴纸。在购买之前,她需要知道有多少剪贴纸,或者她可以用钱买多少套贴纸。玛丽·埃伦怎样才能弄明白这一点呢?

In this concept, you will learn to use intercepts .
::在这个概念中,你会学会使用拦截。

Intercepts
::拦截

Consider the following linear graph.
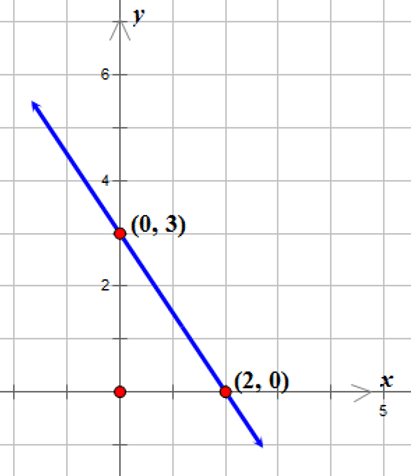
::考虑下线性图。

The above graph models the linear function $\begin{align*}3x+2y=6\end{align*}$ . The function is written in standard form $\begin{align*}Ax+By=C\end{align*}$ . Notice that the line passes through the $\begin{align*}x\end{align*}$ -axis at the point $\begin{align*}(2,0)\end{align*}$ . The point where the graph intersects the horizontal $\begin{align*}x\end{align*}$ -axis is called the $\begin{align*}x\end{align*}$ - intercept . The $\begin{align*}y\end{align*}$ -value of any point on the $\begin{align*}x\end{align*}$ -axis is zero. The $\begin{align*}x\end{align*}$ -axis is really the line having the equation $\begin{align*}y=0\end{align*}$ .
::上图模式的线性函数 3x+2y=6. 函数以标准格式 Ax+By=C 写成。请注意,该线在点(2,0) 穿过 x 轴。该线通过x 轴,该点将水平 x 轴交叉称为 x 界面。x 轴上任何点的 Y 值为零。x 轴实际上是具有 y=0 方程式的线条。

The line also passes through the $\begin{align*}y\end{align*}$ -axis at the point $\begin{align*}(0,3)\end{align*}$ . The point where the graph intersects the vertical $\begin{align*}y\end{align*}$ -axis is called the $\begin{align*}y\end{align*}$ - intercept . The $\begin{align*}x\end{align*}$ -value of any point on the $\begin{align*}y\end{align*}$ -axis is zero. The $\begin{align*}y\end{align*}$ -axis is really the line having the equation $\begin{align*}x=0\end{align*}$ .
::线条在点( 0, 3) 也通过 y 轴。图形交叉垂直 y 轴的点被称为 y 界面。 Y 轴上任何点的 x 值为 0。 Y 轴是具有等式 x=0 的线条。

Remember, only two points are needed to draw a straight line. Therefore , the graph of the linear function $\begin{align*}3x+2y=6\end{align*}$ was drawn by plotting the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts and using a straight edge to join the two plotted points.
::记住, 绘制直线线线条只需要两个点。因此, 线性函数 3x+2y=6 的图形是用绘制 X 和 y 界面, 并使用直边缘加入两个绘图点来绘制的。

From a given function, the intercepts can be determined using algebra. Let’s look at an example.
::从给定的函数中,拦截量可以用代数来确定。让我们来举一个例子。

$\begin{aligned} 5 x - 3 y = 15 \end{aligned}$
$\begin{align*}5x-3y=15\end{align*}$
::5x-3y=15

First, determine the $\begin{align*}x\end{align*}$ -intercept. Substitute $\begin{align*}y=0\end{align*}$ in the equation.
::首先,确定 X 界面。方程中的替代 y=0 。

$\begin{aligned} \begin{array}{rcl} 5 x - 3 y & = & 15 \\ 5 x - 3 (0) & = & 15 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5x-3y &=& 15 \\ 5x-3(0) &=& 15 \end{array}\end{align*}$
::5x-3y=155x-3(0)=15

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 5 x - 3 (0) & = & 15 \\ 5 x - 0 & = & 15 \\ 5 x & = & 15 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5x-3(0) &=& 15 \\ 5x-0 &=& 15 \\ 5x &=& 15 \end{array}\end{align*}$
::5x-3(0)=155x-0=155x=155x=15

Next, divide both sides of the equation by ‘5’ to solve for ‘ $\begin{align*}x\end{align*}$ ’.
::接下来,将等式的两边除以 ' 5 ' , 以解答 'x ' 。

$\begin{aligned} \begin{array}{rcl} 5 x & = & 15 \\ \frac{\overset{1}{5} x}{5} & = & \frac{\overset{3}{15}}{5} \\ x & = & 3 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5x &=& 15 \\ \frac{\overset{1}{\cancel{5}}x}{\cancel{5}} &=& \frac{\overset{3}{\cancel{15}}}{\cancel{5}} \\ x &=& 3 \end{array}\end{align*}$
::5x=1551x5=1535x=3

The answer is 3.
::答案是3

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(3,0)\end{align*}$ .
::x 拦截是 (3,0) 。

Second, determine the $\begin{align*}y\end{align*}$ -intercept. Substitute $\begin{align*}x=0\end{align*}$ in the equation.
::第二,确定 Y 界面。方程式中的替代 x=0 。

$\begin{aligned} \begin{array}{rcl} 5 x - 3 y & = & 15 \\ 5 (0) - 3 y & = & 15 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5x-3y &=& 15 \\ 5(0)-3y &=& 15 \end{array}\end{align*}$
::5x-3y=155(0)-3y=15

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 5 (0) - 3 y & = & 15 \\ 0 - 3 y & = & 15 \\ - 3 y & = & 15 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5(0)-3y &=& 15 \\ 0-3y &=& 15 \\ -3y &=& 15 \end{array}\end{align*}$
::5(0)-3y=150-3y=15-3y=15

Next, divide both sides of the equation by ‘-3’ to solve for ‘ $\begin{align*}y\end{align*}$ ’.
::接下来,将方程式两边除以 ' 3 ' ,

$\begin{aligned} \begin{array}{rcl} - 3 y & = & 15 \\ \frac{\overset{1}{- 3} y}{- 3} & = & \frac{\overset{- 5}{15}}{- 3} \\ y & = & - 5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} -3y &=& 15 \\ \frac{\overset{1}{\cancel{-3}}y}{\cancel{-3}} &=& \frac{\overset{-5}{\cancel{15}}}{\cancel{-3}} \\ y &=& -5 \end{array}\end{align*}$
::-3y=15-31-3=15-5-3-3y=5

The answer is -5.
::答案是 -5

The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0,-5)\end{align*}$ .
::y 界面是 (0,-5) 。

Now, the values of the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts can be used to plot the graph of the linear function $\begin{align*}5x-3y=15\end{align*}$ .
::现在, x 和 y 界面的值可用于绘制线性函数 5x-3y=15 的图。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Mary Ellen and the scrapbooks or stickers. She needs to figure out how many scrapbooks or how many packages of fashion stickers she can buy with her $60.00. How can she do this?
::早些时候,有人给了你一个关于Mary Ellen和剪贴纸或贴纸的问题。她需要弄清楚她能用60美元买到多少剪贴纸或多少套时装贴纸。她怎么能这样做呢?

Mary Ellen can use the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts of a linear function.
::Mary Ellen可以使用线性函数的 X 和 Y 界面。

First, write a linear function to represent the information given.
::首先,写一个线性函数以代表给定的信息。

Let ‘ $\begin{align*}x\end{align*}$ ’ represent the number of scrapbooks that cost $10 each and let ‘ $\begin{align*}y\end{align*}$ ’ represent the number of packages of stickers that cost $5.00 each. She has $60.00 to spend.
::让`x ' 代表每本10美元的废纸数量,让`y ' 代表每张5美元的成套贴纸数量。她有60美元可花。

The linear function to model the given information is:
::用于模拟给定信息的线性函数为:

$\begin{aligned} 10 x + 5 y = 60 \end{aligned}$
$\begin{align*}10x+5y=60\end{align*}$
::10x+5y=60

Next, determine $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts of the linear function.
::下一步,确定线性函数的 X 和 Y 界面。

First, determine the $\begin{align*}x\end{align*}$ -intercept. Substitute $\begin{align*}y=0\end{align*}$ in the equation.
::首先,确定 X 界面。方程中的替代 y=0 。

$\begin{aligned} \begin{array}{rcl} 10 x + 5 y & = & 60 \\ 10 x + 5 (0) & = & 60 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 10x+5y &=& 60 \\ 10x+5(0) &=& 60 \end{array}\end{align*}$
::10x+5y=6010x+5(0)=60

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 10 x + 5 (0) & = & 60 \\ 10 x + 0 & = & 60 \\ 10 x & = & 60 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 10x+5(0) &=& 60 \\ 10x+0 &=& 60 \\ 10x &=& 60 \end{array}\end{align*}$
::10x+5(0)=6010x+0=6010x=60

Next, divide both sides of the equation by ‘10’ to solve for ‘ $\begin{align*}x\end{align*}$ ’.
::接下来,将等式的两边除以 ' 10 ' , 解决 'x ' 。

$\begin{aligned} \begin{array}{rcl} 10 x & = & 60 \\ \frac{\overset{1}{10} x}{10} & = & \frac{\overset{6}{60}}{10} \\ x & = & 6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 10x &=& 60 \\ \frac{\overset{1}{\cancel{10}}x}{\cancel{10}} &=& \frac{\overset{6}{\cancel{60}}}{\cancel{10}} \\ x &=& 6 \end{array}\end{align*}$
::10x=60101x10=60610x=6

The answer is 6.
::答案是6个

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(6,0)\end{align*}$ .
::x 拦截( 6, 0) 。

Second, determine the $\begin{align*}y\end{align*}$ -intercept. Substitute $\begin{align*}x=0\end{align*}$ in the equation.
::第二,确定 Y 界面。方程式中的替代 x=0 。

$\begin{aligned} \begin{array}{rcl} 10 x + 5 y & = & 60 \\ 10 (0) + 5 y & = & 60 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 10x+5y &=& 60 \\ 10(0)+5y &=& 60 \end{array}\end{align*}$
::10x+5y=6010(0)+5y=60

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 10 (0) + 5 y & = & 60 \\ 0 + 5 y & = & 60 \\ 5 y & = & 60 \end{array} \end{aligned}$
$\begin{align*} \begin{array}{rcl} 10(0)+5y &=& 60 \\ 0+5y &=& 60 \\ 5y &=& 60 \end{array}\end{align*}$
::10(0)+5y=600+5y=60

Next, divide both sides of the equation by ‘30’ to solve for ‘ $\begin{align*}y\end{align*}$ ’.
::接下来,将方程式两边除以 '30 ' ,

$\begin{aligned} \begin{array}{rcl} 5 y & = & 60 \\ \frac{\overset{1}{5} y}{5} & = & \frac{\overset{12}{60}}{5} \\ y & = & 12 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 5y &=& 60 \\ \frac{\overset{1}{\cancel{5}}y}{\cancel{5}} &=& \frac{\overset{12}{\cancel{60}}}{\cancel{5}} \\ y &=& 12 \end{array}\end{align*}$
::5y=6051y5=60125y=12

The answer is 12.
::答案是12岁

The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0,12)\end{align*}$ .
::y 界面是 (0, 12) 。

Mary Ellen can buy either 6 scrapbooks and no stickers or 12 packages of stickers and no scrapbooks.
::Mary Ellen既可以买6本剪贴纸,又不能买贴纸,也可以买12包贴纸,也不能买剪贴纸。

Example 2
::例2

For the given linear function, determine the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts.
::对于给定的线性函数,确定 x 和 y 界面。

$\begin{aligned} 4 x - 3 y = - 24 \end{aligned}$
$\begin{align*}4x-3y=-24\end{align*}$
::4-3y24

First, determine the $\begin{align*}x\end{align*}$ -intercept. Substitute $\begin{align*}y=0\end{align*}$ in the equation.
::首先,确定 X 界面。方程中的替代 y=0 。

$\begin{aligned} \begin{array}{rcl} 4 x - 3 y & = & - 24 \\ 4 x - 3 (0) & = & - 24 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 4x-3y &=& -24 \\ 4x-3(0) &=& -24 \end{array}\end{align*}$
::4 - 3y244x-3(0)24

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 4 x - 3 (0) & = & - 24 \\ 4 x - 0 & = & - 24 \\ 4 x & = & - 24 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 4x-3(0) &=& -24 \\ 4x-0 &=& -24 \\ 4x &=& -24 \end{array}\end{align*}$
::4x-3(0)244x-024x24

Next, divide both sides of the equation by ‘4’ to solve for ‘ $\begin{align*}x\end{align*}$ ’.
::接下来,将方程式两边除以 '4 ' ' ' ' ' ' ' ' ' , 解决`x ' 。

$\begin{aligned} \begin{array}{rcl} 4 x & = & - 24 \\ \frac{\overset{1}{4} x}{4} & = & \frac{\overset{- 6}{- 24}}{4} \\ x & = & - 6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 4x &=& -24 \\ \frac{\overset{1}{\cancel{4}}x}{\cancel{4}} &=& \frac{\overset{-6}{\cancel{-24}}}{\cancel{4}} \\ x &=& -6 \end{array}\end{align*}$
::4x 4x2441x4}24-64x#6

The answer is -6.
::答案是 -6

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(-6,0)\end{align*}$ .
::X 拦截( - 6,0) 。

Second, determine the $\begin{align*}y\end{align*}$ -intercept. Substitute $\begin{align*}x=0\end{align*}$ in the equation.
::第二,确定 Y 界面。方程式中的替代 x=0 。

$\begin{aligned} \begin{array}{rcl} 4 x - 3 y & = & - 24 \\ 4 (0) - 3 y & = & - 24 \end{array} \end{aligned}$
$\begin{align*} \begin{array}{rcl} 4x-3y &=& -24 \\ 4(0)-3y &=& -24 \end{array}\end{align*}$
::4x-3y244(0)-3y24

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 4 (0) - 3 y & = & - 24 \\ 0 - 3 y & = & - 24 \\ - 3 y & = & - 24 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 4(0)-3y &=& -24 \\ 0-3y &=& -24 \\ -3y &=& -24 \end{array}\end{align*}$
::4(0)-(3)-(240)-(3)-(24)-(3)-(24)

Next, divide both sides of the equation by ‘-3’ to solve for ‘ $\begin{align*}y\end{align*}$ ’.
::接下来,将方程式两边除以 ' 3 ' ,

$\begin{aligned} \begin{array}{rcl} - 3 y & = & - 24 \\ \frac{\overset{1}{- 3} y}{- 3} & = & \frac{\overset{- 8}{- 24}}{- 3} \\ y & = & 8 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} -3y &=& -24 \\ \frac{\overset{1}{\cancel{-3}}y}{\cancel{-3}} &=& \frac{\overset{-8}{\cancel{-24}}}{\cancel{-3}} \\ y &=& 8 \end{array}\end{align*}$
::- 3 - 24 - 31 - 3 - 24 - 8 - 8 - 3y=8

The answer is 8.
::答案是8岁

The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0, 8)\end{align*}$ .
::y 界面是( 0, 8) 。

Example 2
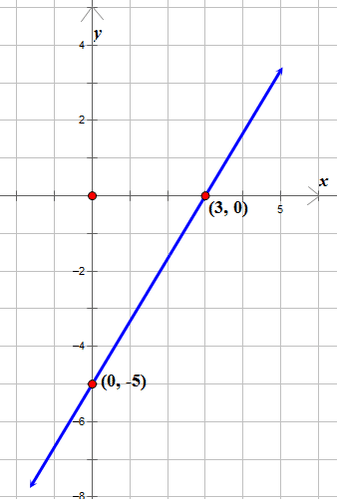
::例2

For the given linear function, use the $\begin{align*}x\end{align*}$ -and $\begin{align*}y\end{align*}$ -intercepts to draw the graph:
::对于给定的线性函数,使用 x 和 y 界面绘制图形:

$\begin{aligned} 6 x - 4 y = 24 \end{aligned}$
$\begin{align*}6x-4y=24\end{align*}$
::6x-4y=24

First, determine the $\begin{align*}x\end{align*}$ -intercept. Substitute $\begin{align*}y=0\end{align*}$ in the equation.
::首先,确定 X 界面。方程中的替代 y=0 。

$\begin{aligned} \begin{array}{rcl} 6 x - 4 y & = & 24 \\ 6 x - 4 (0) & = & 24 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 6x-4y &=& 24 \\ 6x-4(0) &=& 24 \end{array}\end{align*}$
::6x-4y=246x-44(0)=24

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 6 x - 4 (0) & = & 24 \\ 6 x - 0 & = & 24 \\ 6 x & = & 24 \end{array} \end{aligned}$
$\begin{align*} \begin{array}{rcl} 6x-4(0) &=& 24 \\ 6x-0 &=& 24 \\ 6x &=& 24 \end{array}\end{align*}$
::6x-4(0)=246x-0=246x=24

Next, divide both sides of the equation by ‘6’ to solve for ‘ $\begin{align*}x\end{align*}$ ’.
::接下来,将方程式两边除以 '6 ' ' ' ' ' ' ' , 解决`x ' 。

$\begin{aligned} \begin{array}{rcl} 6 x & = & 24 \\ \frac{\overset{1}{6} x}{6} & = & \frac{\overset{4}{24}}{6} \\ x & = & 4 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 6x &=& 24 \\ \frac{\overset{1}{\cancel{6}}x}{\cancel{6}} &=& \frac{\overset{4}{\cancel{24}}}{\cancel{6}} \\ x &=& 4 \end{array}\end{align*}$
::6x=2461x6=2446x=4

The answer is 4.
::答案是4。

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(4,0)\end{align*}$ .
::x 界面为 (4,0) 。

Second, determine the $\begin{align*}y\end{align*}$ -intercept. Substitute $\begin{align*}x=0\end{align*}$ in the equation.
::第二,确定 Y 界面。方程式中的替代 x=0 。

$\begin{aligned} \begin{array}{rcl} 6 x - 4 y & = & 24 \\ 6 (0) - 4 y & = & 24 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 6x-4y &=& 24 \\ 6(0)-4y &=& 24 \end{array}\end{align*}$
::6x-4y=246(0)-4y=24

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 6 (0) - 4 y & = & 24 \\ 0 - 4 y & = & 24 \\ - 4 y & = & 24 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 6(0)-4y &=& 24 \\ 0-4y &=& 24 \\ -4y &=& 24 \end{array}\end{align*}$
::6(0)-4y=240-4y=24-4y=24

Next, divide both sides of the equation by ‘-4’ to solve for ‘ $\begin{align*}y\end{align*}$ ’.
::接下来,将方程式两边除以 ' 4 ' ,

$\begin{aligned} \begin{array}{rcl} - 4 y & = & 24 \\ \frac{\overset{1}{- 4} y}{- 4} & = & \frac{\overset{- 6}{24}}{- 4} \\ y & = & - 6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} -4y &=& 24 \\ \frac{\overset{1}{\cancel{-4}}y}{\cancel{-4}} &=& \frac{\overset{-6}{\cancel{24}}}{\cancel{-4}} \\ y &=& -6 \end{array}\end{align*}$
::− 4y=24-41y-44=24-6-4y=6-6-4y6

The answer is -6.
::答案是 -6

The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0,-6)\end{align*}$ .
::y 界面是 (0, - 6) 。

Now, the values of the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts can be used to plot the graph of the linear function.
::现在, x 和 y 界面的值可用于绘制线性函数的图形。

$\begin{aligned} 6 x - 4 y = 24 \end{aligned}$
$\begin{align*}6x-4y=24\end{align*}$
::6x-4y=24

Example 3
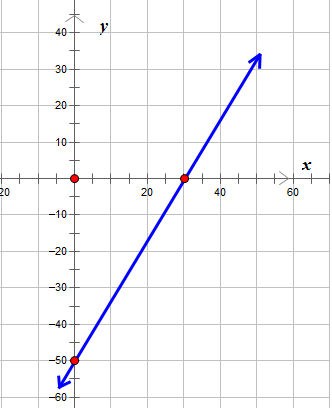
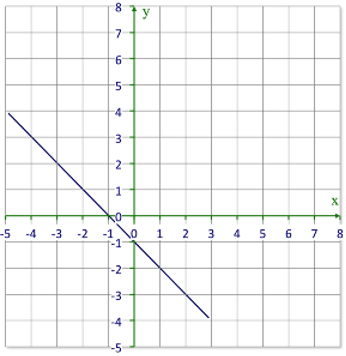
::例3

For the following graph, name the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts.
::下图中,请标明 X 和 y 界面。

The graph crosses the $\begin{align*}x\end{align*}$ -axis at the point $\begin{align*}(30,0)\end{align*}$ and the $\begin{align*}y\end{align*}$ -axis at the point $\begin{align*}(0,-50)\end{align*}$ .
::图表在点(30,0)横过x轴,在点(0,-50)横过Y轴。

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(30,0)\end{align*}$ and the $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0,-50)\end{align*}$ .
::x 拦截( 30,0) , y 拦截( 0,-50) 。

Example 4
::例4

For the given linear function, determine the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -intercepts.
::对于给定的线性函数,确定 x 和 y 界面。

$\begin{aligned} 15 x + 30 y = 120 \end{aligned}$
$\begin{align*}15x+30y=120\end{align*}$
::15x+30y=120

First, determine the $\begin{align*}x\end{align*}$ -intercept. Substitute $\begin{align*}y=0\end{align*}$ in the equation.
::首先,确定 X 界面。方程中的替代 y=0 。

$\begin{aligned} \begin{array}{rcl} 15 x + 30 y & = & 120 \\ 15 x + 30 (0) & = & 120 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 15x+30y &=& 120 \\ 15x+30(0) &=& 120 \end{array}\end{align*}$
::15x+30y=12015x+30(0)=120

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 15 x + 30 (0) & = & 120 \\ 15 x + 0 & = & 120 \\ 15 x & = & 120 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 15x+30(0) &=& 120 \\ 15x+0 &=& 120 \\ 15x &=& 120 \end{array}\end{align*}$
::15x+30(0)=12015x+0=12015x=12015x=120

Next, divide both sides of the equation by ‘15’ to solve for ‘ $\begin{align*}x\end{align*}$ ’.
::接下来,将等式两边除以 ' 15 ' 来解答 'x ' 。

$\begin{aligned} \begin{array}{rcl} 15 x & = & 120 \\ \frac{\overset{1}{15} x}{15} & = & \frac{\overset{8}{120}}{15} \\ x & = & 8 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 15x &=& 120 \\ \frac{\overset{1}{\cancel{15}}x}{\cancel{15}} &=& \frac{\overset{8}{\cancel{120}}}{\cancel{15}} \\ x &=& 8 \end{array}\end{align*}$
::15x=120151x15=120815x=8

The answer is 8.
::答案是8岁

The $\begin{align*}x\end{align*}$ -intercept is $\begin{align*}(8,0)\end{align*}$ .
::X 界面是 8,0 个。

Second, determine the $\begin{align*}y\end{align*}$ -intercept. Substitute $\begin{align*}x=0\end{align*}$ in the equation.
::第二,确定 Y 界面。方程式中的替代 x=0 。

$\begin{aligned} \begin{array}{rcl} 15 x + 30 y & = & 120 \\ 15 (0) + 30 y & = & 120 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 15x+30y &=& 120 \\ 15(0)+30y &=& 120 \end{array}\end{align*}$
::15x+30y=12015(0)+30y=120

Next, perform the multiplication to clear the parenthesis.
::下一步,执行乘法清除括号。

$\begin{aligned} \begin{array}{rcl} 15 (0) + 30 y & = & 120 \\ 0 + 30 y & = & 120 \\ 30 y & = & 120 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 15(0)+30y &=& 120 \\ 0+30y &=& 120 \\ 30y &=& 120 \end{array}\end{align*}$
::15(0)+30y=1200+30y=12030y=120

Next, divide both sides of the equation by ‘30’ to solve for ‘ $\begin{align*}y\end{align*}$ ’.
::接下来,将方程式两边除以 '30 ' ,

$\begin{aligned} \begin{array}{rcl} 30 y & = & 120 \\ \frac{\overset{1}{30} y}{30} & = & \frac{\overset{4}{120}}{30} \\ y & = & 4 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 30y &=& 120 \\ \frac{\overset{1}{\cancel{30}}y}{\cancel{30}} &=& \frac{\overset{4}{\cancel{120}}}{\cancel{30}} \\ y &=& 4 \end{array}\end{align*}$
::30y=120301y30=120430y=4

The answer is 4.
::答案是4。

The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}(0,4)\end{align*}$ .
::Y 界面是 0, 4 。

Review
::回顾

Determine the $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ -intercepts of each equation. There will be two answers for each equation.
::确定每个方程式的 x 和 Y 界面。每个方程式将有两个答案。

1. $\begin{align*}3x + 4y = 12\end{align*}$
::1. 3x+4y=12

2. $\begin{align*}6x + 2y = 12\end{align*}$
::2. 6x+2y=12

3. $\begin{align*}4x + 5y = 20\end{align*}$
::3. 4x+5y=20

4. $\begin{align*}4x + 2y = 8\end{align*}$
::4. 4x+2y=8

5. $\begin{align*}3x + 5y = 15\end{align*}$
::5. 3x+5y=15

6. $\begin{align*}-2x + 3y = -6\end{align*}$
::6.-2x+3y=6

7. $\begin{align*}-3x + y = 9\end{align*}$
::7.-3x+y=9

8. $\begin{align*}-2x- 2y = 6\end{align*}$
::8.-2x-2y=6

9. $\begin{align*}7x + 3y = 21\end{align*}$
::9. 7x+3y=21

10. $\begin{align*}2x + 9y = 36\end{align*}$
::10. 2x+9y=36

Look at each graph and identify the $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ -intercept of each equation. Each graph will have two answers.
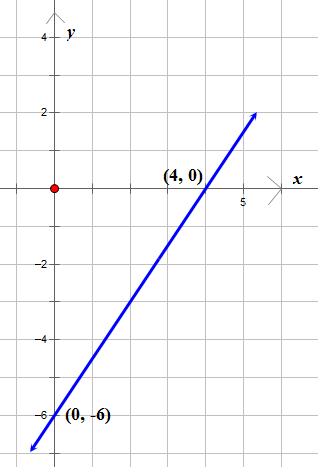
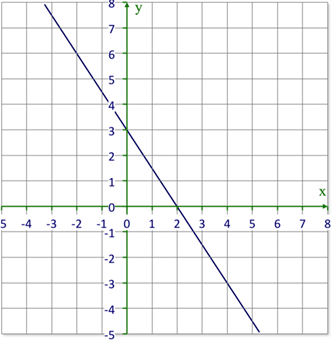
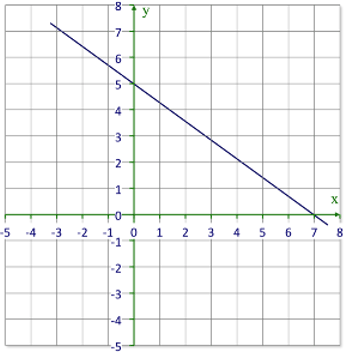
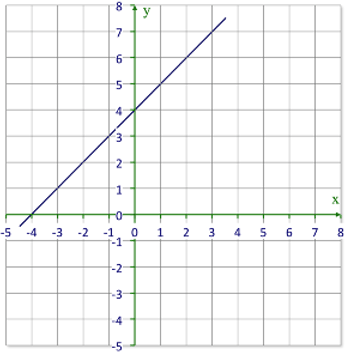
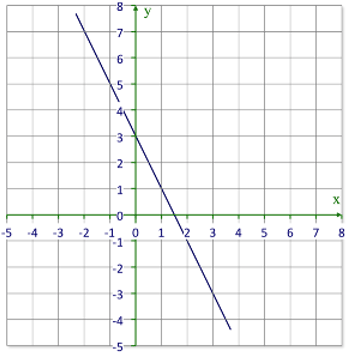
::查看每个图形, 并识别每个方程式的 x 和 Y 界面。每个图形将有两个答案。

11.

12.

13.

14.

15.

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

使用拦截

Intercepts ::拦截

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Intercepts
::拦截

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)