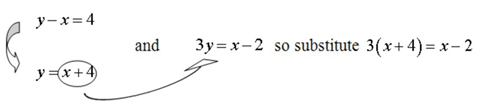课程： 9.15 通过替代解决线性线性系统

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节以替代方式解决线性系统

折叠展开
以替代方式解决线性系统
Kathleen’s rectangular garden has a perimeter of 280 yards. The length is three times the width. If she wants to buy fencing panels to surround it , then Kathleen must determine the garden's dimensions .
::Kathleen的长方形花园周边有280码。长幅是宽度的三倍。如果她想买围栏板围住它,那么Kathleen必须确定花园的尺寸。

How can Kathleen use a system of equations to calculate the length and width of her rectangular garden?
::Kathleen如何使用一个方程系统来计算她的长宽花园?

In this concept, you will learn to solve linear systems by substitution.
::在这个概念中,你将学会通过替代解决线性系统。

Substitution Method
::替代方法

There is an ordered pair $\begin{aligned} (x, y) \end{aligned}$ that makes both equations in the following system of linear equations true. This means that ‘ $\begin{aligned} x \end{aligned}$ ’ in the first equation equals ‘ $\begin{aligned} x \end{aligned}$ ’ in the second equation and ‘ $\begin{aligned} y \end{aligned}$ ’ in the first equation equals ‘ $\begin{aligned} y \end{aligned}$ ’ in the second equation.
::有一个定购对(x,y)使以下线性方程系统中的两个方程都是真的。这意味着第一个方程中的 " x " 等于第二个方程中的 " x " ,第一个方程中的 "y " 等于第二个方程中的 "y " 。

$\begin{aligned} \begin{array}{rcl} 3 y & = & x - 2 \\ y - x & = & 4 \end{array} \end{aligned}$

::3y=x-2y-x=4 3y=x-2y-x=4

The solution to a system of two linear equations with two variables $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ is a value for $\begin{aligned} x \end{aligned}$ and a value for $\begin{aligned} y \end{aligned}$ that will make both equations true. One way to find these values for the variables is by using the substitution method. The substitution method involves solving one of the equations for one of the variables and replacing that variable in the other equation with its equivalent expression . The result will be an equation with one variable which can be solved using algebra.
::由两个变量 x 和 y 组成的两个线性方程式系统的解决方案是两个变量 x 和 y 的值,它将使两个方程式都成为真实。找到这些变量的数值的一个方法是使用替代方法。替代方法涉及解决其中一个变量的方程式之一,并将另一个方程式中的变量替换为等效表达式。结果将是一个带有一个变量的方程式,该变量可以用代数解析。

Let’s solve the given system of linear equations using the substitution method.
::让我们使用替代方法解决给定的线性方程式系统。

$\begin{aligned} \begin{array}{rcl} 3 y & = & x - 2 \\ y - x & = & 4 \end{array} \end{aligned}$

::3y=x-2y-x=4 3y=x-2y-x=4

First, solve the second equation for the variable $\begin{aligned} y \end{aligned}$ by adding $\begin{aligned} x \end{aligned}$ to both sides of the equation.
::首先,通过在公式的两侧添加 x 来解析变量 y 的第二个方程式。

$\begin{aligned} \begin{array}{rcl} y - x & = & 4 \\ y - x + x & = & 4 + x \end{array} \end{aligned}$

::yx=4y-x+x=4+x yx=4+x

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

$\begin{aligned} \begin{array}{rcl} y - x + x & = & 4 + x \\ y & = & 4 + x \end{array} \end{aligned}$

::- yx+x=4+xy=4+x - yx+x=4+x

Next, substitute this expression for $\begin{aligned} y \end{aligned}$ into the first equation.
::接下来,将此表达式替换为 y , 在第一个方程中。

$\begin{aligned} \begin{array}{rcl} y & = & 4 + x \\ 3 y & = & x - 2 \\ 3 (4 + x) & = & x - 2 \end{array} \end{aligned}$

::y=4+x3y=x-23(4+x)=x-2

Next, do the multiplication on the left side of the equation to clear " data-term="Parentheses" role="term" tabindex="0"> parentheses .
::下一步,在方程左侧进行乘法以清除括号。

$\begin{aligned} \begin{array}{rcl} 3 (4 + x) & = & x - 2 \\ 12 + 3 x & = & x - 2 \end{array} \end{aligned}$

::3(4+x)=x-212+3x=x-2

Next, subtract 12 from both sides of the equation and simplify.
::接下来,从方程的两侧减去12,并简化。

$\begin{aligned} \begin{array}{rcl} 12 + 3 x & = & x - 2 \\ 12 - 12 + 3 x & = & x - 2 - 12 \\ 3 x & = & x - 14 \end{array} \end{aligned}$

::12+3x=x-212-212-12+3x=x-2-2-123x=x-14

Next, subtract $\begin{aligned} x \end{aligned}$ from both sides of the equation and simplify to isolate the variable on one side.
::下一步,从方程的两侧减去 x ,并简化以将变量单侧分离出来。

$\begin{aligned} \begin{array}{rcl} 3 x & = & x - 14 \\ 3 x - x & = & x - x - 14 \\ 2 x & = & - 14 \end{array} \end{aligned}$

::3x=x-143x-x=x-x-x-x--142x=14

Then, divide both sides of the equation by 2 to solve for the variable $\begin{aligned} x . \end{aligned}$
::然后,将方程两边除以 2 以解析变量 x 。

$\begin{aligned} \begin{array}{rcl} 2 x & = & - 14 \\ \overset{1}{\frac{2 x}{2}} & = & - \overset{7}{\frac{14}{2}} \\ x & = & - 7 \end{array} \end{aligned}$

::2x142x21}1427x7

Next, substitute the value for $\begin{aligned} x \end{aligned}$ into the expression for $\begin{aligned} y \end{aligned}$ and simplify the right side of the equation.
::接下来,将 x 的值替换为 Y 的表达式,并简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} y & = & 4 + x \\ y & = & 4 + (- 7) \\ y & = & 4 - 7 \\ y & = & - 3 \end{array} \end{aligned}$

::y=4+xy=4+(-7)y=4-7y3

The answer is $\begin{aligned} x = - 7 \end{aligned}$ and $\begin{aligned} y = - 3 \end{aligned}$ .
::答案是 x7 和 y3 。

The solution for the system of linear equations is:
::线性方程式系统的解决办法是:

$\begin{aligned} (\binom{x}{y}) = (\binom{- 7}{- 3}) \end{aligned}$

:xy)=(-7-3)

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Kathleen and her rectangular garden. She needs to figure out the dimensions of the garden. How can Kathleen use a system of equations to help her figure this out?
::早些时候,有人给了你关于凯思琳和她的长方形花园的问题。她需要弄清楚花园的尺寸。凯思琳如何使用方程式系统来帮助她解决这个问题?

First, write a system of linear equations to represent the information given in the story.
::首先,写一个线性方程式系统来代表故事中提供的信息。

Let $\begin{aligned} l \end{aligned}$ represent length and let $\begin{aligned} w \end{aligned}$ represent the width.
::我代表长度,我代表宽度。

The length of the garden is three times the width and the perimeter is 280 yards.
::花园的长度是宽度的3倍,周边是280码。

$\begin{aligned} \begin{array}{rcl} l & = & 3 w \\ 2 l + 2 w & = & 280 \end{array} \end{aligned}$

::l=3w2l+2w=280

Next, substitute the expression for $\begin{aligned} l \end{aligned}$ into the second equation.
::接下来,用I的表达方式替换第二个方程。

$\begin{aligned} \begin{array}{rcl} l & = & 3 w \\ 2 (3 w) + 2 w & = & 280 \end{array} \end{aligned}$

::l=3w2(3w)+2w=280

Next, perform the multiplication on the left side of the equation to clear parentheses and simplify.
::下一步,在方程左侧执行乘法,以清除括号并简化。

$\begin{aligned} \begin{array}{rcl} 2 (3 w) + 2 w & = & 280 \\ 6 w + 2 w & = & 280 \\ 8 w & = & 280 \end{array} \end{aligned}$

::2(3w)+2w=2806w+2w=2808w=280

Next, divide both sides of the equation by 8 to solve for $\begin{aligned} w \end{aligned}$ .
::接下来,将方程式的两边除以 8 来解答 w 。

$\begin{aligned} \begin{array}{rcl} 8 w & = & 280 \\ \overset{1}{\frac{8 w}{8}} & = & \overset{35}{\frac{280}{8}} \\ w & = & 35 \end{array} \end{aligned}$

::8w=2808w81=280835w=35

The answer is 35.
::答案是35岁

The width of the garden is 35 yards.
::花园宽度是35码

Next, substitute the value for $\begin{aligned} w \end{aligned}$ into the expression for the variable $\begin{aligned} l \end{aligned}$ and simplify the right side of the equation.
::接下来,将变量 1 的表达式中的 w 值替换为变量 1,并简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} l & = & 3 w \\ l & = & 3 (35) \\ l & = & 105 \end{array} \end{aligned}$

::1=3wl=3(35)l=105

The answer is 105.
::答案是105

The length of the garden is 105 yards.
::花园的长度是105码

The solution for the system of linear equations is $\begin{aligned} (\binom{w}{l}) = (\binom{35}{105}) \end{aligned}$ which means the dimensions of Kathleen’s garden are 35 yards by 105 yards.
::线性方程式系统的解决方案是 (wl) = (35105) , 这意味着Kathleen 花园的尺寸是35码乘105码。

Example 2
::例2

Solve the following system of linear equations using the substitution method.
::使用替代方法解决下列线性方程系统。

$\begin{aligned} \begin{array}{rcl} 2 x + 3 y & = & 6 \\ x + y & = & 6 \end{array} \end{aligned}$

::2x+3y=6x+y=6

First, solve the second equation for the variable $\begin{aligned} x \end{aligned}$ by subtracting $\begin{aligned} y \end{aligned}$ from both sides of the equation.
::首先,从方程两侧减去 y 以解析变量 x 的第二个方程。

$\begin{aligned} \begin{array}{rcl} x + y & = & 6 \\ x + y - y & = & 6 - y \end{array} \end{aligned}$

::x+y=6x+y-y=6-y

Next, simplify the left side of the equation.
::接下来,简化方程的左侧。

$\begin{aligned} \begin{array}{rcl} x + y - y & = & 6 - y \\ x & = & 6 - y \end{array} \end{aligned}$

::x+y-yy=6-yx=6-yy

Next, substitute this expression for $\begin{aligned} x \end{aligned}$ into the first equation.
::接下来,将 X 替换为第一个方程。

$\begin{aligned} \begin{array}{rcl} x & = & 6 - y \\ 2 x + 3 y & = & 6 \\ 2 (6 - y) + 3 y & = & 6 \end{array} \end{aligned}$

::x=6-y2x+3y=62(6-y)+3y=6

Next, do the multiplication on the left side of the equation to clear parentheses.
::下一步,在方程左侧进行乘法以清除括号。

$\begin{aligned} \begin{array}{rcl} 2 (6 - y) + 3 y & = & 6 \\ 12 - 2 y + 3 y & = & 6 \end{array} \end{aligned}$

::2(6-y)+3y=612-2y+3y=6

Next, simplify the left side of the equation.
::接下来,简化方程的左侧。

$\begin{aligned} \begin{array}{rcl} 12 - 2 y + 3 y & = & 6 \\ 12 + y & = & 6 \end{array} \end{aligned}$

::12-2y+3y=612+y=612+y=6

Next, subtract 12 from both sides of the equation to solve for the variable $\begin{aligned} y . \end{aligned}$
::下一步,从方程两侧减去 12 ,以解析变量 y 。

$\begin{aligned} \begin{array}{rcl} 12 + y & = & 6 \\ 12 - 12 + y & = & 6 - 12 \end{array} \end{aligned}$

::12+y=612 - 12+y=6-12

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

$\begin{aligned} \begin{array}{rcl} 12 - 12 + y & = & 6 - 12 \\ y & = & - 6 \end{array} \end{aligned}$

::12 - 12+y=6 - 12y=6 - 12y=6

Next, substitute the value for $\begin{aligned} y \end{aligned}$ into the expression for $\begin{aligned} x \end{aligned}$ and simplify the right side of the equation.
::接下来,将 Y 的值替换为 x 的表达式,并简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} x & = & 6 - y \\ x & = & 6 - (- 6) \\ x & = & 6 + 6 \\ x & = & 12 \end{array} \end{aligned}$

::x=6-yx=6-(-6)x=6+6x=12

The answer is $\begin{aligned} x = 12 \end{aligned}$ and $\begin{aligned} y = - 6 \end{aligned}$ .
::答案是 x=12 和 y6 。

The solution for the system of linear equations is:
::线性方程式系统的解决办法是:

$\begin{aligned} (\binom{x}{y}) = (\binom{12}{- 6}) \end{aligned}$

:xy)=(12-6)

Example 3
::例3

Solve the following system of linear equations using the substitution method.
::使用替代方法解决下列线性方程系统。

$\begin{aligned} \begin{array}{rcl} 2 y & = & x + 4 \\ y & = & 3 x \end{array} \end{aligned}$

::2y=x+4y=3x

First, substitute the expression for $\begin{aligned} y \end{aligned}$ into the first equation.
::首先,将y的表达方式替换为第一个方程。

$\begin{aligned} \begin{array}{rcl} y & = & 3 x \\ 2 y & = & x + 4 \\ 2 (3 x) & = & x + 4 \end{array} \end{aligned}$

::y=3x2y=x+42(3x)=x+4

Next, perform the multiplication on the left side of the equation to clear parentheses.
::下一步,在方程左侧执行乘法以清除括号。

$\begin{aligned} \begin{array}{rcl} 2 (3 x) & = & x + 4 \\ 6 x & = & x + 4 \end{array} \end{aligned}$

::2(3x)=x+46x=x+4

Next, subtract $\begin{aligned} x \end{aligned}$ from both sides of the equation and simplify to isolate the variable on one side.
::下一步,从方程的两侧减去 x ,并简化以将变量单侧分离出来。

$\begin{aligned} \begin{array}{rcl} 6 x & = & x + 4 \\ 6 x - x & = & x - x + 4 \end{array} \end{aligned}$

::6x=x+46x-x=x-x+4 6x=x+46x-x=x-x+4

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

$\begin{aligned} \begin{array}{rcl} 6 x - x & = & x - x + 4 \\ 5 x & = & 4 \end{array} \end{aligned}$

::6-x=x-x+45x=4

Next, divide both sides of the equation by 5 to solve for the variable $\begin{aligned} x . \end{aligned}$
::接下来,将方程两边除以 5 以解析变量 x 。

$\begin{aligned} \begin{array}{rcl} 5 x & = & 4 \\ \overset{1}{\frac{5}{5} x} & = & \frac{4}{5} \\ x & = & \frac{4}{5} \end{array} \end{aligned}$

::5x=455x1=45x=45

Next, substitute the value for $\begin{aligned} x \end{aligned}$ into the expression for $\begin{aligned} y \end{aligned}$ and simplify the right side of the equation.
::接下来,将 x 的值替换为 Y 的表达式,并简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} y & = & 3 x \\ y & = & 3 (\frac{4}{5}) \\ y & = & \frac{12}{5} \end{array} \end{aligned}$

The answer is $\begin{aligned} x = \frac{4}{5} \end{aligned}$ and $\begin{aligned} y = \frac{12}{5} \end{aligned}$ .
::y=3xy=3(45y=125) 答案是 x=45和y=125。

The solution for the system of linear equations is:
::线性方程式系统的解决办法是:

$\begin{aligned} (\binom{x}{y}) = (\binom{\frac{4}{5}}{\frac{12}{5}}) \end{aligned}$

:xy)=(45125)

Example 4
::例4

Solve the following system of linear equations using the substitution method.
::使用替代方法解决下列线性方程系统。

$\begin{aligned} \begin{array}{rcl} x + y & = & 4 \\ 2 x - 3 y & = & 18 \end{array} \end{aligned}$

::x+y=42x-3y=18

First, solve the first equation for the variable ‘ $\begin{aligned} x \end{aligned}$ ’ by subtracting ‘ $\begin{aligned} y \end{aligned}$ ’ from both sides of the equation.
::首先,解决变量 ' x ' 的第一个方程,从方程的两侧减去`y ' 。

$\begin{aligned} \begin{array}{rcl} x + y & = & 4 \\ x + y - y & = & 4 - y \end{array} \end{aligned}$

::x+y=4x+y-y=4-y

Next, simplify the left side of the equation.
::接下来,简化方程的左侧。

$\begin{aligned} \begin{array}{rcl} x + y - y & = & 4 - y \\ x & = & 4 - y \end{array} \end{aligned}$

::x+y-y=4-yx=4-yy

Next, substitute this expression for ‘ $\begin{aligned} x \end{aligned}$ ’ into the first equation.
::接下来,用这个表达式代替第一个方程式中的 'x ' 。

$\begin{aligned} \begin{array}{rcl} x & = & 4 - y \\ 2 x - 3 y & = & 18 \\ 2 (4 - y) - 3 y & = & 18 \end{array} \end{aligned}$

::x=4-y2x-3y=182(4-y)--3y=18

Next, do the multiplication on the left side of the equation to clear parentheses.
::下一步,在方程左侧进行乘法以清除括号。

$\begin{aligned} \begin{array}{rcl} 2 (4 - y) - 3 y & = & 18 \\ 8 - 2 y - 3 y & = & 18 \end{array} \end{aligned}$

::2(4-y)-3y=188-2y-3y=18

Next, simplify the left side of the equation.
::接下来,简化方程的左侧。

$\begin{aligned} \begin{array}{rcl} 8 - 2 y - 3 y & = & 18 \\ 8 - 5 y & = & 18 \end{array} \end{aligned}$

::8-2y-3y=188-5y=18

Next, subtract 8 from both sides of the equation to isolate the variable ‘ $\begin{aligned} y \end{aligned}$ ’.
::接下来,从方程的两侧减去8,以孤立变量“y”。

$\begin{aligned} \begin{array}{rcl} 8 - 5 y & = & 18 \\ 8 - 8 - 5 y & = & 18 - 8 \end{array} \end{aligned}$

::8-5y=188-8-8-8-5y=18-8

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

$\begin{aligned} \begin{array}{rcl} 8 - 8 - 5 y & = & 18 - 8 \\ - 5 y & = & 10 \end{array} \end{aligned}$

::8-8-5y=18-8-8-5y=10

Next, divide both sides of the equation by -5 to solve for the variable ‘ $\begin{aligned} y \end{aligned}$ ’.
::接下来,将方程的两边除以 - 5, 以解析变量“ Y” 。

$\begin{aligned} \begin{array}{rcl} - 5 y & = & 10 \\ \overset{1}{\frac{- 5}{- 5} y} & = & \overset{- 2}{\frac{10}{- 5}} \\ y & = & - 2 \end{array} \end{aligned}$

::-5y=10-5-5-5-5y1=10-5-2y2

Next, substitute the value for ‘ $\begin{aligned} y \end{aligned}$ ’ into the expression for ‘ $\begin{aligned} x \end{aligned}$ ’ and simplify the right side of the equation.
::接下来,将 "y " 的值替换为 " x " 的表达式,简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} x & = & 4 - y \\ x & = & 4 - (- 2) \\ x & = & 4 + 2 \\ x & = & 6 \end{array} \end{aligned}$

The answer is $\begin{aligned} x = 6 \end{aligned}$ and $\begin{aligned} y = - 2 \end{aligned}$ .
::x=4-yx=4- (- 2x=4+2x=6) 答案是 x=6 和 y2 。

The solution for the system of linear equations is:
::线性方程式系统的解决办法是:

$\begin{aligned} (\binom{x}{y}) = (\binom{6}{- 2}) \end{aligned}$

:xy)=(6-2)

Example 5
::例5

Solve the following system of linear equations using the substitution method.
::使用替代方法解决下列线性方程系统。

$\begin{aligned} \begin{array}{rcl} 3 y & = & x - 22 \\ y & = & 4 x \end{array} \end{aligned}$

::3y=x-22y=4x

First, substitute the expression for ‘ $\begin{aligned} y \end{aligned}$ ’ into the first equation.
::首先,在第一个方程式中用 "y " 代替 "y " 。

$\begin{aligned} \begin{array}{rcl} y & = & 4 x \\ 3 y & = & x - 22 \\ 3 (4 x) & = & x - 22 \end{array} \end{aligned}$

::y=4x3y=x-223(4x)=x-22

Next, perform the multiplication on the left side of the equation to clear parentheses.
::下一步,在方程左侧执行乘法以清除括号。

$\begin{aligned} \begin{array}{rcl} 3 (4 x) & = & x - 22 \\ 12 x & = & x - 22 \end{array} \end{aligned}$

::3(4x)=x-2212x=x-22

Next, subtract ‘ $\begin{aligned} x \end{aligned}$ ’ from both sides of the equation and simplify to isolate the variable on one side.
::接下来,从方程的两侧减去 'x ' ,并简化以将变量分离成一边。

$\begin{aligned} \begin{array}{rcl} 12 x & = & x - 22 \\ 12 x - x & = & x - x - 22 \end{array} \end{aligned}$

::12x=x-2212x-x=x-x-x-x-22

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

$\begin{aligned} \begin{array}{rcl} 12 x - x & = & x - x - 22 \\ 11 x & = & - 22 \end{array} \end{aligned}$

::12-x=x-x-x- 2211xx @ @ 22

Next, divide both sides of the equation by 11 to solve for the variable ‘ $\begin{aligned} x \end{aligned}$ ’ .
::接下来,将方程的两边除以 11, 以解析变量 'x' 。

$\begin{aligned} \begin{array}{rcl} 11 x & = & - 22 \\ \overset{1}{\frac{11}{11} x} & = & \overset{- 2}{\frac{- 22}{11}} \\ x & = & - 2 \end{array} \end{aligned}$

::11x#221111x1#2211_2x#2

Next, substitute the value for ‘ $\begin{aligned} x \end{aligned}$ ’ into the expression for ‘ $\begin{aligned} y \end{aligned}$ ’ and simplify the right side of the equation.
::其次,将`x ' 值改为`y ' 值,简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} y & = & 4 x \\ y & = & 4 (- 2) \\ y & = & - 8 \end{array} \end{aligned}$

The answer is $\begin{aligned} x = - 2 \end{aligned}$ and $\begin{aligned} y = - 8 \end{aligned}$ .
::y= 4xy= 4 (- 2) y8 答案是 x\\ 2 和 y8 。

The solution for the system of linear equations is:
::线性方程式系统的解决办法是:

$\begin{aligned} (\binom{x}{y}) = (\binom{- 2}{- 8}) \end{aligned}$

:xy)=(-2-8)

Review
::回顾

Solve each linear system by substitution.
::通过替代解决每个线性系统。

1. $\begin{aligned} \begin{array}{rcl} y & = & 8 \\ 2 y + 2 x & = & 2 \end{array} \end{aligned}$
::1.y=82y+2x=2

2. $\begin{aligned} \begin{array}{rcl} x & = & 16 \\ 2 y + 2 x & = & 2 \end{array} \end{aligned}$
::2. x=162y+2x=2

3. $\begin{aligned} \begin{array}{rcl} 2 x & = & 8 \\ 2 y + x & = & 10 \end{array} \end{aligned}$
::3. 2x=82y+x=10

4. $\begin{aligned} \begin{array}{rcl} 3 y & = & 9 \\ y + 2 x & = & 11 \end{array} \end{aligned}$
::4. 3y=9y+2x=11

5. $\begin{aligned} \begin{array}{rcl} y - 8 & = & 8 \\ 2 y + x & = & 20 \end{array} \end{aligned}$
::5. y-8=82y+x=20

6. $\begin{aligned} \begin{array}{rcl} 4 y & = & 8 \\ y - 2 x & = & 8 \end{array} \end{aligned}$
::6. 4y=8y-2x=8

7. $\begin{aligned} \begin{array}{rcl} x - 2 & = & 4 \\ 4 x + y & = & 12 \end{array} \end{aligned}$
::7. x-2=44x+y=12

8. $\begin{aligned} \begin{array}{rcl} y & = & x + 8 \\ y + 2 x & = & 11 \end{array} \end{aligned}$
::8. y=x+8y+2x=11

9. $\begin{aligned} \begin{array}{rcl} 2 y + 8 & = & 12 \\ y + 2 x & = & 20 \end{array} \end{aligned}$
::9. 2y+8=12y+2x=20

10. $\begin{aligned} \begin{array}{rcl} y - 3 & = & 6 \\ 3 y + 3 x & = & 9 \end{array} \end{aligned}$
::y-3=63y+3x=9

11. $\begin{aligned} \begin{array}{rcl} 4 y - 1 & = & 11 \\ y - 4 x & = & 5 \end{array} \end{aligned}$
::11. 4y-1=11y-4x=5

12. $\begin{aligned} \begin{array}{rcl} 2 y - 8 & = & 8 \\ 2 y + 2 x & = & 2 \end{array} \end{aligned}$
::12. 2y-8=82y+2x=2

13. $\begin{aligned} \begin{array}{rcl} 4 x + y & = & - 2 \\ - 2 x - 3 y & = & 1 \end{array} \end{aligned}$
::13. 4x+y2-2x-3y=1

14. $\begin{aligned} \begin{array}{rcl} y & = & 2 x \\ 6 x - y & = & 8 \end{array} \end{aligned}$
::14. y=2x6x-y=8

15. $\begin{aligned} \begin{array}{rcl} x + 4 y & = & - 6 \\ 2 x + 10 y & = & - 6 \end{array} \end{aligned}$
::15. x+4y 62x+10y6

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

以替代方式解决线性系统

Substitution Method ::替代方法

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Substitution Method
::替代方法

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)