章节大纲

  • 常规

    全部折叠 展开全部

  • 承认差异

    lesson content

    Sandra, Janet, and Karen want to have their picture taken. The photographer wants to put them in a line for the picture, but the girls can’t decide who should be in the middle and how they should arrange themselves. They ask the photographer if they can take a shot in every possible arrangement and then choose their favorite. How many different arrangements can the three girls be in for their picture?
    ::桑德拉、珍妮特和凯伦想拍下他们的照片。 摄影师想把照片排成一行,但女孩们不能决定谁是中间的,如何安排自己。 她们问摄影师能否在各种可能的安排下拍一张照片,然后选择最喜欢的。 三个女孩可以做多少不同安排来拍照?

    In this concept, you will learn to recognize permutations in situations where order is important.
    ::在这一概念中,在秩序重要的情况下,你们将学会认识差异。

    Permutations
    ::差异

    Order is important in some situations and not important in others. For example, in following a cake recipe, the order in which the events take place is important. You need to crack the eggs before you mix them with the flour. Similarly, you put the icing on the cake only after it has baked.
    ::秩序在某些情况下很重要,但在另一些情况下不重要。 例如, 在遵循蛋糕食谱时, 事件发生的顺序很重要 。 您需要先把鸡蛋和面粉混合起来。 同样, 您只能在蛋糕烤熟后才能在蛋糕上加结冰 。

    In buying the ingredients to make a cake, on the other hand, order is not important. Does it matter if you buy the flour before the eggs or the milk before the icing? It doesn’t, so you would say that order is not important in buying cake ingredients.
    ::另一方面,在购买做蛋糕的原料时,订购并不重要。 如果你在鸡蛋前买面粉,或者在结冰前买牛奶,这是否重要? 它并不重要,所以你会说,在购买蛋糕原料时,顺序并不重要。

    For solving many problems in which order is important, you can use permutations . A is a selection of items in which order is important. To use permutations to solve problems, you need to be able to identify the problems in which order, or the arrangement of items, matters.
    ::为了解决许多按顺序排列的问题,您可以使用变式。A是选择按顺序排列的项目。要使用变式来解决问题,您必须能够找出按顺序排列或安排项目所涉及的问题。

    Let’s look at an example.
    ::让我们举个例子。

    Jack has a lock on his locker. When opening his locker, does order matter? Is this a permutation?
    ::杰克的储物柜上锁了,打开储物柜时,订货有关系吗?

    The lock combination is particular to each lock. For example if Jack’s combination was 35 − 17 − 23 , it would only open if he uses these numbers in this order. Order is therefore important and this is a permutation.
    ::锁组合对每个锁都是特别的。 例如,如果杰克的组合是35-17-23,那么只有他用这些数字按此顺序使用,它才会打开。 因此,秩序是重要的,这是一个变换。

    You can count permutations too. There is a mathematical way to calculate the number of permutations possible given the number of items selected.
    ::您也可以计算排列。根据所选项目的数量,有数学方法计算可能的排列次数。

    To count the number of permutations in a problem you need to look at the problem as a series of choices. You can find the number of permutations in a group if you include all members of that group.
    ::要计算问题中的变异次数, 您需要将问题作为一系列选择来看待。 如果您包括一个组的所有成员, 您可以在组中找到变异次数 。

    Let’s look at an example.
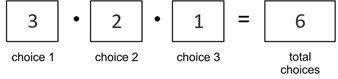
    ::让我们举个例子。

    Suppose there are 3 cabs in front of a hotel, Acme, Bluebird, and Checker. If all 3 line up to wait for the next customer, the number of different lineups, or permutations, of 3 items taken 3 at a time is:
    ::假设酒店、 Acme、Bluebird 和 Checker 前面有三辆出租车。 如果所有三辆计程车都排成排队等待下一位顾客, 不同的排队数或调换数, 3辆列队数, 一次3辆列队数是:

    lesson content

    Again, this is the permutation for three cabs lined up three at a time. You could also say that this is three objects taken three at a time.
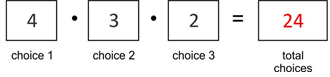
    ::再说一遍,这是三辆计程车每次排成三辆的变换。你也可以说这是三件物体,一次三件。

    What happens when 4 cabs show up at the hotel, but there is only room for 3 cabs to line up? For example, how many different 3-cab lineups would there be if you started with 4 cabs – Acme, Bluebird, Checker, and Decker?
    ::4辆计程车在酒店出现,但只有3辆计程车排队,会发生什么情况? 比如,如果你先坐4辆计程车,Acme、Bluebird、Cecker和Decker,那么,3辆计程车排成几辆不同的3个计程车会有多少?

    Now, for choice 1 you have four choices instead of three.
    ::现在,对于选择1,你有四个选择,而不是三个。

    lesson content

    For the choice 2 you have three 3 choices instead of two and for choice 3 you have two choices instead of one. The final calculation gives 24 total choices:
    ::对于选择2,你有三个三个选择,而不是两个选择;对于选择3,你有两个选择,而不是一个选择。最后计算得出24个总选择:

    lesson content

    This is the answer when you have four options taken three at a time.
    ::这是答案,当你有四个选项时, 一次选择三个选项 。

    Examples
    ::实例

    Example 1
    ::例1

    Earlier, you were given a problem about  Janet, Sandra and Karen having their picture taken.
    ::早些时候,你被问及珍妮特,桑德拉和凯伦 拍摄他们的照片的问题。

    Three girls are getting their picture taken and the photographer wants them to line up.
    ::三个女孩正在拍照 摄影师要她们排队

    You need to determine the number of permutations there are for the three girls to be in a line.
    ::三个女孩要排成一行 需要确定变异数量

    First, look at the problem.
    ::首先,看看问题。

    If one of the three girls is put in the first spot, two of the girls will be placed in the second and the last girl remaining will be placed in the third spot.
    ::如果将3个女孩中的1个放在第一地点,其中2个女孩放在第二地点,剩下的最后一个女孩放在第三地点。

    Next, calculate the number of choices.
    ::接下来,计算选择的数量。

    P ( spot 1, spot 2, spot 3 ) = 3 × 2 × 1 P ( spot 1, spot 2, spot 3 ) = 6

    ::P( 第1点, 第1点, 第2点, 第2点, 第3点) = 3x2x1P( 第1点, 第2点, 第3点) =6

    The answer is 6.
    ::答案是6个

    There are 6 different ways Sandra, Karen, and Janet could be lined up for their picture.
    ::桑德拉和凯伦有六种不同的方式 珍妮特可以排队拍照

    Example 2
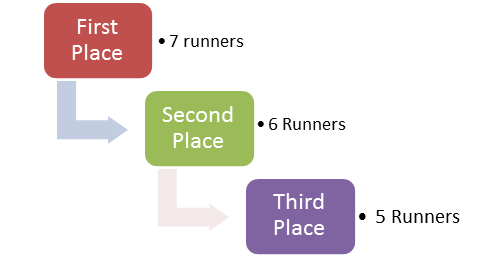
    ::例2

    Seven people are in a race. Determine how many choices there are for first, second, and third place.
    ::七个人在比赛中,决定第一、第二和第三位有多少选择。

    First, let’s think about the problem. For first place, any seven of the runners could possibly win. For second place, six of the remaining runners could come in second. Five of the remaining runners could come in third.
    ::首先,让我们考虑一下问题。 首先,任何七个选手都有可能获胜。 第二,剩下的六个选手可能第二。 剩下的五个选手可能第三。

    Next, find the number of choices for first, second, and third.
    ::接下来,找到第一、第二、第三选择的数量。

    lesson content

    Then, calculate the number of choices.
    ::然后计算选择的数量。

    P ( first, second, third ) = 7 × 6 × 5 P ( first, second, third ) = 210

    ::P(第一、第二、第三)=7x6x5P(第一、第二、第三)=210

    The answer is 210.
    ::答案是210

    There are 210 different ways these seven runners could take first, second, and third place in the race.
    ::这七个选手有210种不同的方式 在比赛中第一,第二,第三位

    Example 3
    ::例3

    If five people want to go to the movies, but there are only two seats available, how many ways can the people sit if they can only sit two at a time?
    ::如果有五个人想去看电影, 但只有两个座位, 人民能坐上多少种方式,

    First, let’s think about the problem.
    ::首先,让我们考虑一下这个问题。

    There are only two seats and there are five people. Any of the five people can be the first person to sit in one of the seats. Any of the remaining four people could take the second of the two seats.
    ::只有两个席位,有五个人,五个人中的任何一个都可以是第一个坐在其中一个席位上的人,其余四个人中的任何一个可以占据两个席位中的第二个。

    Next, calculate the number of choices.
    ::接下来,计算选择的数量。

    P ( seat 1, seat 2 ) = 5 × 4 P ( seat 1, seat 2 ) = 20

    ::P(座位1,座位2)=5×4P(座位1,座位2)=20

    The answer is 20.
    ::答案是20岁

    There are 20 different ways these five people could sit in the two available seats at the movies.
    ::这五个人有20种不同的方式 可以坐在电影的两个座位上。

    Example 4
    ::例4

    How many different ways could the people be seated if there were three seats?
    ::如果有三个席位,人们能坐上多少种不同的座位?

    First, let’s think about the problem.
    ::首先,让我们考虑一下这个问题。

    There are only three seats and there are five people. Any of the five people can be the first person to sit in one of the seats. Any of the remaining four people could take the second of the three seats. The remaining three people could be seated in the final empty seat.
    ::只有三个席位,有五个人,五个人中的任何一个都可以是第一个坐在其中一个席位上的人,其余四个人中的任何一个可以占三个席位中的第二个,其余三个人可以坐在最后一个空席位上。

    Next, calculate the number of choices.
    ::接下来,计算选择的数量。

    P ( seat 1, seat 2, seat 3 ) = 5 × 4 × 3 P ( seat 1, seat 2, seat 3 ) = 60

    ::P(座位1,座位2,座位3)=5×4×3P(座位1,座位2,座位3)=60

    The answer is 60.
    ::答案是60岁

    There are 60 different ways these five people could sit in the three available seats at the movies.
    ::这五个人有60种不同的方式 坐在电影的三个座位上。

    Example 5
    ::例5

    How many different ways could the people be seated if there were four seats?
    ::如果有四个座位,人们能坐上多少种不同的座位?

    First, let’s think about the problem.
    ::首先,让我们考虑一下这个问题。

    There are only four seats and there are five people. Any of the five people can be the first person to sit in one of the seats. Any of the remaining four people could take the second of the four seats. Three people remain for the last two seats. The remaining two people could be seated in the final empty seat.
    ::只有四个席位,五个人,五个人中的任何一个都可以是第一个坐在一个席位上的人,剩下的四个人中的任何一个都可以占四个席位中的第二个席位,最后两个席位只剩下三个人,剩下的两个人可以坐在最后一个空席位上。

    Next, calculate the number of choices.
    ::接下来,计算选择的数量。

    P ( seat 1, seat 2, seat 3, seat 4 ) = 5 × 4 × 3 × 2 P ( seat 1, seat 2, seat 3, seat 4 ) = 120

    ::P(座位1,座位2,座位3,座位4)=5×4×3×2P(1,座位2,座位3,座位4)=120

    The answer is 120.
    ::答案是120个

    There are 120 different ways these five people could sit in the four available seats at the movies.
    ::这五个人可以用120种不同的方式 坐在电影的4个座位上。

    Review
    ::回顾

    Figure out each permutation or each outcome.
    ::找出每个变异或结果。

    1. Four different frogs entered the jumping contest -Spots, Dots, Slimey, and Croaky. In how many ways can the 4 finish in first, second, third, and fourth place?
    ::1. 四个不同的青蛙参加了跳跃比赛 -- -- Spots、Dots、Dots、Slimey和Croaky,四只青蛙在第一、第二、第三和第四位可以完成多少次?

    2. Denise has the letters A, R, X, O, G, I, and L. How many different 4-letter arrangements can she make?
    ::2. Denise有字母A、R、X、O、G、I和L。 她能作出多少不同的4字母安排?

    3. Six people have signed up to play Scrabble –Tim, Jim, Kim, Pam, Sam, and Cam. Only 4 people can play at one time. How many different 4-player games are possible?
    ::3. 六人已报名参加拼字游戏-Tim、Jim、Kim、Pam、Sam和Cam,只有四人可以同时玩游戏,可以玩多少场不同的四人游戏?

    4. Arnold printed out his 8-page report without putting page numbers on the pages. Now the pages have gotten all mixed up. In how many different ways can Arnold arrange the 8 pages?
    ::4. 阿诺德打印了8页的报告,没有把页码放在页码上,现在页数混淆了,阿诺德能用多少种不同的方式安排8页?

    5. The special lunch at Bamboo Restaurant gives you a choice of won-ton or hot-sour soup, a choice of kung pao shrimp or chicken with broccoli, and a choice rice or noodles. How many different special lunches are there?
    ::5. 在竹布餐厅的特别午餐,你可选择圆顿汤或热汤,选择有西兰花的功夫保马虾或鸡肉,以及选择大米或面条,有多少不同的特别午餐?

    6. Rex forgot the password for his ATM bank card. He knows that the password is made of the 4 digits of his birthday, October 24 or 1, 0, 2, 4.? How many different passwords does he need to try to be sure he gets his password?
    ::6. 雷克斯忘记了自动取款机银行卡的密码,他知道密码是他10月24日生日四位数或10月1日、0日、2日、4日的4位数的密码,他需要多少不同的密码才能确保他得到密码?

    7. Javier wrote out wrote out the letters of Jasmine’s name on 7 cupcakes and put them in a box. How many different ways can he take them out of the box one by one?
    ::7. 哈维尔在7个纸杯蛋糕上写下了茉莉名字的字母,并把它们放入一个盒子里,他能用多少种不同的方式把它们逐个从盒子里拿出来?

    8. On the new reality show, Lazybones, the five finalists –Snoozin’ Betty, Lounge Man, The Yawn Meister, Lana Later, and Bob the Procrastinator –compete to see who is the laziest person. On today’s show, the five will be weeded down to 3 super-finalists. How many different ways can the 3 super-finalists be chosen?
    ::8. 在新的现实节目中,Lazybones,五个决赛选手 — — 贝蒂、休息室人、Yawn Meister、拉纳后来和巴勃(Procratistinator) — — 竞相看看谁是最懒的人。 在今天的节目中,这五个选手将被选为3个超级决赛选手。 3个超级决赛选手可以选用多少种不同的方式?

    9. Four friends have printed the letters M, E, T, S on the front of their shirts. They’re going to the Mets game and will sit in 4 seats side by side. In how many different ways can the four sit?
    ::9. 四个朋友在衬衫前印了M、E、T、S的信,他们要去参加大都会比赛,坐在四个座位上,四人可以坐多少种方式?

    10. How many different 3-digit numbers can you form from the digits 4, 5, and 6?
    ::10. 从数字4、5和6中,你可形成多少不同的三位数?

    Use permutations to solve each problem.
    ::使用变式来解决每个问题。

    11. How many 3-digit numbers can Blanche write using the digits 7, 8, and 9?
    ::11. Blanche用数字7、8和9能写出多少三位数?

    12. How many 4-letter arrangements can Blanche write using the letters A, B, C, D?
    ::12. Blanche用字母A、B、C、D可以写多少四字母安排?

    13. The programmer for Oddball-TV has 5 new half-hour shows she wants to air on Tuesday evenings: Strange Days, Slightly Off, Odd Rod, Bent, and Icky the Great. In how many different orders can she present the shows?
    ::13. Oddball-TV的程序员有5个新的半小时节目,她想在星期二晚上播出:奇事日、微小脱节、奥德罗德、本特和艾克基大帝。

    14. A train has 6 different cars –a passenger car, a baggage car, a mail car, a diner car, a freight car, and a caboose. In how many different orders can the cars be arranged?
    ::14. 一列火车有6辆不同的汽车——一辆客车、一辆行李车、一辆邮车、一辆餐车、一辆货运车和一辆卡波斯汽车。

    15. The last 5 digits of Beryl’s phone number are 34567. How many numbers have these same 5 digits?
    ::15. 贝里尔最后5位数的电话号码是34567,有多少数字是相同的5位数?

    16. Mia has 7 charms for her charm bracelet –a heart, a moon, a turtle, a cube, a bird, a hoop, and a car. Into how many different orders can she arrange the 7 charms?
    ::16. 米娅的魅力手镯有7种魅力——一颗心脏、一颗月亮、一只乌龟、一只立方体、一只鸟、一只圈和一辆车。

    Review (Answers)
    ::回顾(答复)

    Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
    ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

     

    Resources
    ::资源