Course: 11.4 使用变换名称表评估变换情况

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 使用变换名称表评价变异

Collapse Expand
使用变换名称表评价变异
Donna works at the library. She is arranging the new science fiction books that have come in. She only has room for six of the 20 new books on her shelf. How many different arrangements can be made when six books are chosen from a group of 20 books to be placed on a shelf?
::Donna在图书馆工作,她正在安排新科幻小说,新书已经送来。她只有6本新书的位子,20本新书中只有6本在她的架子上。如果从一组20本书中选出6本书放在架子上,那么可以作出多少不同的安排?

In this concept, you will learn to evaluate permutations by using permutation notation .
::在此概念中,您将学会使用变换符号来评估变异。

Permutations
::差异

The Counting Principle states that if event can be chosen in $\begin{aligned} p \end{aligned}$ different ways and an independent event is chosen in $\begin{aligned} q \end{aligned}$ different ways, the probability of the two events occurring in $\begin{aligned} p \times q \end{aligned}$ . Basically, this tells you how many ways you can arrange items. A is a selection of items in which order is important. To use permutations to solve problems, you need to be able to identify the problems in which order, or the arrangement of items, matters.
::计数原则指出,如果事件可以以 p 不同的方式选择,而独立事件可以以q 不同的方式选择,那么在 pxq. 中发生两个事件的概率基本上就说明了您可以安排项目的方式。 A 是选择按顺序排列的项目。要用变相来解决问题, 您需要能够找出项目顺序或排列事项的问题。

Let’s look at an example.
::让我们举个例子。

How many ways can you arrange the letters in the word MATH?
::你能用多少方法来安排MATH这个字里的信?

First, look at the problem.
::首先,看看问题。

You have 4 letters in the word and you are going to choose one letter at a time. When you choose the first letter, you have 4 possibilities (M, A, T, or H), your second choice will be 3 possibilities, third choice will be 2 possibilities (because there are only 2 letters left to choose from), and last choice only one possibility.
::您在单词中有 4 个字母, 您将同时选择一个字母。当您选择第一个字母时, 您有 4 个选项( M、 A、 T 或 H) , 您的第二个选项是 3 个选项, 第三个选项是 2 个选项( 因为只有 2 个字母可供选择) , 最后一个选项只有 1 个选项。

Next, calculate the number of choices.
::接下来,计算选择的数量。

$\begin{aligned} P (choice 1, choice 2, choice 3, choice 4) = 4 \times 3 \times 2 \times 1 \\ P (choice 1, choice 2, choice 3, choice 4) = 24 \end{aligned}$

::P(选择1,选择2,选择3,选择4)=4×3×2×1P(选择1,选择2,选择3,选择4)=24

The answer is 24.
::答案是24个。

There are 24 different ways to arrange the letters in the word MATH.
::有24种不同的方式来安排字母在MATH这个词。

The most efficient way to calculate permutations uses numbers called . Factorials are special numbers that represent the product of a series of descending numbers.
::计算变异的最有效方式是使用被称为。阶乘数是特殊数字, 代表一系列递减数字的产物。

The symbol for a is an exclamation sign.
::a 的符号是一个感叹符号。

Take a look at how factorials are used.
::看一下系数值是如何使用的。

$\begin{aligned} 8 factorial = 8! = 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \end{aligned}$
::8 乘数= 8! =8x7x6x5x4x4x3x3x2x1

$\begin{aligned} 11 factorial = 11! = 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \end{aligned}$
::11 因数=11! =11x10x9x8x7x6x6x5x4x3x2x1

$\begin{aligned} 4 factorial = 4! = 4 \times 3 \times 2 \times 1 \end{aligned}$
::4 阶乘= 4!= 4x3x2x1

$\begin{aligned} 17 factorial = 17! = 17 \times 16 \times 15 \times 14 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \end{aligned}$
::17 因数=17!=17x16x15x14x13x12x12x11x10x9x8x7x7x6x5x4x3x3x2x1

To compute the values of factorials, simply multiply the series of numbers.
::要计算系数值,只需乘以数字序列。

$\begin{aligned} \begin{array}{rcl} 4 factorial = 4! & = & 4 \times 3 \times 2 \times 1 \\ = & 24 \\ 6 factorial = 6! & = & 6 \times 5 \times 4 \times 3 \times 2 \times 1 \\ = & 720 \\ 8 factorial = 8! & = & 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \\ = & 40, 320 \end{array} \end{aligned}$

::4 因数=4!=4x3x2x1=246因数=6!=6x5x4x4x3x3x2x1=7208因数=8!=8x7x6x5x5x4x3x3x2x1=40,320

You can also use a graphing calculator to find factorials. For large numbers, especially, the calculator can save you time.
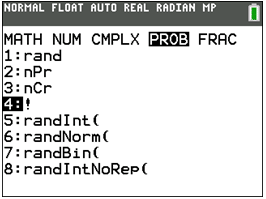
::也可以使用图形计算器来查找阶乘。对于大数字,特别是对于大数字,计算器可以节省时间。

If you push the $\begin{aligned} m \end{aligned}$ button and on the top of the screen you will see PROB. #4 under the PROB menu is factorial.
::如果您按下 m 按钮并在屏幕上方, 您将会看到 PROB 。在 PROB 菜单下, # 4 是因数。

Let’s try an example.
::让我们以身作则。

Find 10! using your calculator.
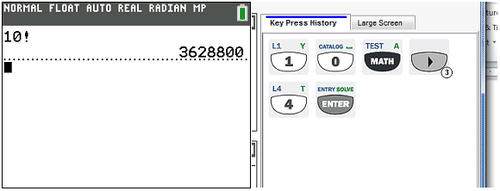
::找到10,用你的计算器

The answer is 3628800. Notice the key press history to tell you what was pressed to get 10!
::答案是 3628800 。注意关键媒体历史, 告诉您按什么按10 !

You can use factorials to calculate permutations. Look at the formula for finding permutations.
::您可以使用乘数来计算变数。查看查找变数的公式。

In general, permutations are written as:
::一般说来,变式的写法是:

$\begin{aligned} _{n} P_{r} = n items taken r at a time \end{aligned}$

::nPr=一次拍摄的项目 r

To compute $\begin{aligned} _{n} P_{r} \end{aligned}$ you write:
::要计算 nPr, 您要写入 :

$\begin{aligned} _{n} P_{r} = \frac{n!}{(n - r)!} \end{aligned}$

::NPRN! !

Let’s look at an example.
::让我们举个例子。

Suppose you have 6 items and you want to know how many arrangements you can make with 4 of the items.
::假设你有6个项目,你想知道有多少安排你可以做与4个项目。

First, order matters in this problem, so you need to find the number of permutations there are in 6 items taken 4 at a time.
::首先,这个问题的顺序问题, 所以你需要找到6个项目中的变异数量, 一次4个。

First, in permutation notation write the following.
::首先,在变换符号中写下以下文字。

$\begin{aligned} _{6} P_{4} = \end{aligned}$ 6 items taken 4 at a time
::6P4=6件,一次4件,每次4件

Next, calculate $\begin{aligned} _{6} P_{4} \end{aligned}$ .
::接下来,计算6P4。

$\begin{aligned} \begin{array}{rcl} _{n} P_{r} & = & \frac{n!}{(n - r)!} \\ _{6} P_{4} & = & \frac{6!}{(6 - 4)!} \\ _{6} P_{4} & = & \frac{6!}{2!} \\ _{6} P_{4} & = & \frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1} \\ _{6} P_{4} & = & 6 \times 5 \times 4 \times 3 \\ _{6} P_{4} & = & 360 \end{array} \end{aligned}$

::nPr=n!!! (n-r)! 6P4=6! (6- 4)! 6P4=6! 2.! 6P4=6x5x5x4x3x3x2x12x16P4=6x5x4x36P4=360

Notice that it is the product of the values in descending order that tells you how many permutations are possible. You can use this method to solve any number of permutations.
::注意是数值按降序排列的产物,它告诉您有多少变异是可能的。您可以使用这个方法来解决任何数量的变异。

You can also use the graphing calculator to find $\begin{aligned} _{n} P_{r} \end{aligned}$ . If you push the m button and on the top of the screen you will see PROB. #2 under the PROB menu is $\begin{aligned} _{n} P_{r} \end{aligned}$ .
::您也可以使用图形计算器查找 nPr。如果您按下 m 按钮并在屏幕顶部, 您将会看到 PROB。 PROB 菜单下的 # 2 是 nPr 。

To find $\begin{aligned} _{8} P_{3} \end{aligned}$ using the calculator, you would get the following. Notice the key press history to tell you what to press to do $\begin{aligned} _{8} P_{3} \end{aligned}$ .
::要使用计算器找到 8P3, 您可以得到以下信息。注意关键媒体历史, 告诉您要按什么按什么按 8P 3 。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Donna the librarian.
::之前,你被问起图书馆管理员唐娜的事

Donna is trying to choose six books of her 20 new books to put on the shelf. Remember that order is important and repetition is not allowed, so permutations must be used.
::Donna正试图从她的20本新书中挑选六本书,放在架子上。记住,这个命令很重要,不允许重复,所以必须使用变换。

Donna has 20 books to choose from, therefore $\begin{aligned} n = 20 \end{aligned}$ . She will choose 6 books, therefore $\begin{aligned} r = 6 \end{aligned}$ .
::唐娜有20本书可供选择, 因此, n=20。她将选择6本书, 因此 r=6 。

First, fill in the formula for $\begin{aligned} _{n} P_{r} \end{aligned}$ where $\begin{aligned} n = 20 \end{aligned}$ and $\begin{aligned} r = 6 \end{aligned}$ .
::首先,填写nPr的公式,其中n=20和r=6。

$\begin{aligned} \begin{array}{rcl} _{n} P_{r} & = & \frac{n!}{(n - r)!} \\ _{20} P_{6} & = & \frac{20!}{(20 - 6)!} \end{array} \end{aligned}$

::20P6=20! 20P6=6! 20P6=6!

Next, compute $\begin{aligned} _{20} P_{6} \end{aligned}$ .
::下一个,计算20P6。

$\begin{aligned} \begin{array}{rcl} _{20} P_{6} & = & \frac{20!}{(20 - 6)!} \\ _{20} P_{6} & = & \frac{20!}{14!} \\ _{20} P_{6} & = & \frac{20 \times 19 \times 18 \times 17 \times 16 \times 15 \times 14 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{14 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} \\ _{20} P_{6} & = & 20 \times 19 \times 18 \times 17 \times 16 \times 15 \\ _{20} P_{6} & = & 27907200 \end{array} \end{aligned}$

::20P6=20! 20P6=20! (20- 6)! 20P6=20! 14.! 20P6=20P6=20. 14! 20P6=20x1918x18x17x17x1615x14x13x12x12xx11xxxxxxxxxxxxxxxxx10x6xxx5x5xxx4x8x7xxxxxxx12xxxxxx1111xx10xxxx10xxxx9x8x6xxxxxxxxxxx2xx120P6=20P=27907200

The answer is 27907200.
::答案是27907200

There are 27,907,200 different ways Donna can choose six books of the 20 to display on the shelf.
::有27 907 200种不同的方式唐娜可以选择六本书在20本书的架子上展示

Example 2
::例2

Find $\begin{aligned} _{7} P_{3} \end{aligned}$ .
::查找 7P3。

First, fill in the formula for $\begin{aligned} _{n} P_{r} \end{aligned}$ where $\begin{aligned} n = 7 \end{aligned}$ and $\begin{aligned} r = 3 \end{aligned}$ .
::首先,填写nPr的公式,其中n=7和r=3。

$\begin{aligned} \begin{array}{rcl} _{n} P_{r} & = & \frac{n!}{(n - r)!} \\ _{7} P_{3} & = & \frac{7!}{(7 - 3)!} \end{array} \end{aligned}$

::nPr=n! 7P3=7! (7- 3)!

Next, compute $\begin{aligned} _{7} P_{3} \end{aligned}$ .
::下一个,计算7P3。

$\begin{aligned} \begin{array}{rcl} _{7} P_{3} & = & \frac{7!}{(7 - 3)!} \\ _{7} P_{3} & = & \frac{7!}{4!} \\ _{7} P_{3} & = & \frac{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{4 \times 3 \times 2 \times 1} \\ _{7} P_{3} & = & 7 \times 6 \times 5 \\ _{7} P_{3} & = & 210 \end{array} \end{aligned}$

::7P3=7! 7P3=7!! 7P3=7! 4! 7P3=7x6x5x5x4x3x3xx2x14x3x3x217P3=7x6x57P3=210

The answer is 210.
::答案是210

Example 3
::例3

Find $\begin{aligned} _{4} P_{3} \end{aligned}$ .
::查找 4P3 。

First, fill in the formula for $\begin{aligned} _{n} P_{r} \end{aligned}$ where $\begin{aligned} n = 4 \end{aligned}$ and $\begin{aligned} r = 3 \end{aligned}$ .
::首先,填写nPr的公式,其中 n=4 和 r=3。

$\begin{aligned} \begin{array}{rcl} _{n} P_{r} & = & \frac{n!}{(n - r)!} \\ _{4} P_{3} & = & \frac{4!}{(4 - 3)!} \end{array} \end{aligned}$

::nPr=n! 4P3=4! (4- 3)!

Next, compute $\begin{aligned} _{4} P_{3} \end{aligned}$ .
::下一个,计算 4P3。

$\begin{aligned} \begin{array}{rcl} _{4} P_{3} & = & \frac{4!}{(4 - 3)!} \\ _{4} P_{3} & = & \frac{4!}{1!} \\ _{4} P_{3} & = & \frac{4 \times 3 \times 2 \times 1}{1} \\ _{4} P_{3} & = & 4 \times 3 \times 2 \times 1 \\ _{4} P_{3} & = & 24 \end{array} \end{aligned}$

::4P3=4!!( 4) 4P3=4! 1! 4P3=4! 1! 4P3=4x3x2x2x114P3=4x3x2x14P3=24

The answer is 24.
::答案是24个。

Example 4
::例4

Find $\begin{aligned} _{12} P_{2} \end{aligned}$ .
::找12P2 12P2 12P2 12P2 12P2 finding 12P2.

First, fill in the formula for $\begin{aligned} _{n} P_{r} \end{aligned}$ where $\begin{aligned} n = 12 \end{aligned}$ and $\begin{aligned} r = 2 \end{aligned}$ .
::首先,填写nPr的公式,其中 n=12 和 r=2。

$\begin{aligned} \begin{array}{rcl} _{n} P_{r} & = & \frac{n!}{(n - r)!} \\ _{12} P_{2} & = & \frac{12!}{(12 - 2)!} \end{array} \end{aligned}$

::NPR=n! 12P2=12! (12- 2)!

Next, compute $\begin{aligned} _{12} P_{2} \end{aligned}$ .
::下一个,计算12P2。

$\begin{aligned} \begin{array}{rcl} _{12} P_{2} & = & \frac{12!}{(12 - 2)!} \\ _{12} P_{2} & = & \frac{12!}{10!} \\ _{12} P_{2} & = & \frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} \\ _{12} P_{2} & = & 12 \times 11 \\ _{12} P_{2} & = & 132 \end{array} \end{aligned}$

::12P2=12! 12P2=12 12P2=12! 10! 12P2=12x11x10x9x8x7x6xx6x5x5x4x3x2xx110x9x8x7x6x5x5x4x3xx12P2=12x1112P2=132

The answer is 132.
::答案是132

Example 5
::例5

Find $\begin{aligned} _{8} P_{6} \end{aligned}$ .
::查找 8P6 。

First, fill in the formula for $\begin{aligned} _{n} P_{r} \end{aligned}$ where $\begin{aligned} n = 8 \end{aligned}$ and $\begin{aligned} r = 6 \end{aligned}$ .
::首先,填写nPr的公式,其中 n=8 和 r=6。

$\begin{aligned} \begin{array}{rcl} _{n} P_{r} & = & \frac{n!}{(n - r)!} \\ _{8} P_{6} & = & \frac{8!}{(8 - 6)!} \end{array} \end{aligned}$

::nPr=n! ! 8P6=8! (8-6)!

Next, compute $\begin{aligned} _{8} P_{6} \end{aligned}$ .
::下一个,计算 8P6 。

$\begin{aligned} \begin{array}{rcl} _{8} P_{6} & = & \frac{8!}{(8 - 6)!} \\ _{8} P_{6} & = & \frac{8!}{2!} \\ _{8} P_{6} & = & \frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1} \\ _{8} P_{6} & = & 8 \times 7 \times 6 \times 5 \times 4 \times 3 \\ _{8} P_{6} & = & 20160 \end{array} \end{aligned}$

::8P6=8!! (8- 6)! 8P6=8! 2! 8P6=8x7x6x6x5x4x3x3x2x12x18P6=8x7x6x5x438P6=20160

The answer is 20,160.
::答案是20,160

Review
::回顾

Find each permutation.
::找到每一个变异体

1. Find $\begin{aligned} _{7} P_{2} \end{aligned}$
::1. 7P2

2. Find $\begin{aligned} _{6} P_{3} \end{aligned}$
::2. 6P3

3. Find $\begin{aligned} _{5} P_{4} \end{aligned}$
::3. 参见5P4

4. Find $\begin{aligned} _{5} P_{5} \end{aligned}$
::4. 5P5

5. Find $\begin{aligned} _{9} P_{3} \end{aligned}$
::5. 找9P3

6. Find $\begin{aligned} _{9} P_{7} \end{aligned}$
::6. 参见9P7

7. Find $\begin{aligned} _{11} P_{3} \end{aligned}$
::7. 参见11P3

8. Find $\begin{aligned} _{12} P_{3} \end{aligned}$
::8. 参见12P3

9. Find $\begin{aligned} _{6} P_{2} \end{aligned}$
::9. 6P2

10. Find $\begin{aligned} _{14} P_{3} \end{aligned}$
::10. 查找14P3

11. Find $\begin{aligned} _{15} P_{3} \end{aligned}$
::11. 15P3

12. Find $\begin{aligned} _{11} P_{4} \end{aligned}$
::12. 查找11P4

13. Find $\begin{aligned} _{16} P_{2} \end{aligned}$
::13. 16P2

Use permutations to solve each problem.
::使用变式来解决每个问题。

14. Mia has 7 charms for her charm bracelet – a heart, a moon, a turtle, a cube, a bird, a hoop, and a car. Into how many different orders can she arrange the 7 charms?
::14. 米娅的魅力手镯有7种魅力 — — 心脏、月亮、乌龟、立方体、鸟、圈圈和汽车。她能安排7种魅力手镯多少种不同的订单?

15. One of the charms in Mia’s bracelet in problem 6 above fell off. How many fewer arrangements are there now?
::15. 上面问题6中米娅手镯的魅力之一掉下来了,现在有多少安排更少?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

Section outline

General

使用变换名称表评价变异

Permutations ::差异

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Permutations
::差异

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源