课程： 11.14 了解几何概率

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节理解几何概率

折叠展开
理解几何概率
Emma and Abby were looking at a picture of a stunt bike rider. The picture was of a bicyclist riding down a piece of pipe. In fact, the pipe had been split into two separate pieces and the bicyclist was able to ride on both pieces of the pipe.
::Emma和Abby正在看一部特技自行车骑手的照片。照片上是一位骑自行车的骑手骑着一根管子。事实上,管子被分割成两块,而骑自行车的骑手能够骑着管子的两块。

“I made one of those once,” Emma’s dad said looking at the article. “You start with a 10 foot piece of pipe. Then you metal saw it into two separate pieces. You hope that your work is accurate and that you end up with a piece that is about 7 feet or longer. That way you can really ride down before the quick turn”.
::Emma的爸爸说,“我做过一次,”她的父亲看着这篇文章说,“你先从一根10英尺长的管子开始,然后你用金属把管子分成两块,你希望你的作品准确无误,最后的作品大约为7英尺或更长,这样你就可以在快速转弯之前真正地骑下来了”。

“What are the chances that the pipe is split like that?” Abby asked.
::Abby问道,“管道裂开的可能性有多大?”

In this concept, you will learn to use geometric probability in problem solving.
::在这个概念中,你会学会使用几何概率解决问题。

Geometric Probability
::几何概率

Geometric probability is the probability associated with a geometric problem. The best way to think about geometric probability is through a real-world situation.
::几何概率是与几何问题相关的概率。考虑几何概率的最佳方法是通过现实世界的情况。

Let’s look at an example.
::让我们举个例子。

If a circle with a radius of 10 inches is placed inside a square with a side length of 20 inches, what is the probability that a dart thrown will land inside the circle?
::如果半径为10英寸的圆圈位于方形内,侧长为20英寸的方形内,投掷的飞镖在圆圈内降落的可能性有多大?

First, find the area of the circle.
::首先,找到圆圈的区域。

$\begin{aligned} \begin{array}{rcl} A & = & π r^{2} \\ A & = & π (10)^{2} \\ A & = & 314 i n^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A & = & \pi r^2\\ A & = & \pi (10)^2\\ A & = & 314 \ in^2 \end{array}\end{align*}$
::Ar2A( 10) 2A=314 英寸 2

Next, find the area of the square.
::下一个,找到广场的面积。

$\begin{aligned} \begin{array}{rcl} A & = & s^{2} \\ A & = & 20^{2} \\ A & = & 400 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A & = & s^2\\ A & = & 20^2\\ A & = & 400 \end{array}\end{align*}$
::A=S2A=202A=400

Then, use the formula for probability to solve the problem.
::然后,使用概率公式来解决问题。

For this problem a favorable outcome would be hitting the circle. Therefore the number of favorable outcomes would be the area of the circle. The total outcomes would be the area of the square since the square covers the circle.
::对于这个问题,一个有利的结果将是撞击圆圈。因此,有利的结果数目将是圆圈的面积。总结果将是平方的面积,因为平方覆盖圆圈。

$\begin{aligned} \begin{array}{rcl} P (event) & = & \frac{# of favorable outcomes}{total # of outcomes} \\ P (landing in circle) & = & \frac{A_{circle}}{A_{square}} \\ P (landing in circle) & = & \frac{314}{400} \\ P (landing in circle) & = & 0.785 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P (\text{event}) &=& \frac{\# \ \text{of favorable outcomes}}{\text{total} \ \# \ \text{of outcomes}} \\ P (\text{landing in circle}) &=& \frac{A_{\text{circle}}}{A_{\text{square}}} \\ P (\text{landing in circle}) &=& \frac{314}{400} \\ P (\text{landing in circle}) &=& 0.785 \end{array}\end{align*}$
::P(活动) +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

The answer is 0.785.
::答案是0.785。

The probability of a dart being thrown and hitting the circle is 0.785 or 78.5%.
::抛掷飞镖并撞击圆圈的概率为0.785或78.5%。

Let’s look at another example.
::让我们再看看另一个例子。

As a joke, a tennis player on the left side of the court who was attempting to place his serve into service box $\begin{align*}A\end{align*}$ hit a serve straight up in the air as high as he could. The ball landed on the green side of the court in some random location.
::开个玩笑,法庭左侧的网球手试图把他的球员放在A号服务箱中,他尽可能地在空中直直击球。球在某个随机地点落在球场的绿面上。

What is the probability that the serve landed in the service box $\begin{align*}A\end{align*}$ ?
::服务到达服务箱A的概率是多少?

First, calculate the area of box $\begin{align*}A\end{align*}$ , box $\begin{align*}B\end{align*}$ , and box $\begin{align*}C\end{align*}$ . You can look at the diagram to determine this. Remember that the formula for the area of a rectangle is $\begin{align*}A = lw\end{align*}$ and the units are measured in square units. In this case, it will be square feet.
::首先,计算框A、框B和框C的面积。您可以查看图表来确定这一点。记住矩形区域的公式是 A=lw, 单位用平方单位计量。在这种情况下, 它将是平方英尺。

$\begin{aligned} \begin{array}{rcl} A r e a_{B o x A} & = & l \times w \\ = & 21 f t \times 13.5 f t \\ = & 283.5 f t^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} Area_{Box \ A} &=& l \times w \\ &=& 21 \ ft \times 13.5 \ ft \\ &=& 283.5 \ ft^2 \end{array}\end{align*}$
::区域Box A=lxw=21 ftx13.5 ft=283.5 ft2 区域Box A=lxw=21 ftx13.5 ft=283.5 ft2

$\begin{aligned} \begin{array}{rcl} A r e a_{B o x B} & = & l \times w \\ = & 21 f t \times 13.5 f t \\ = & 283.5 f t^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} Area_{Box \ B} &=& l \times w \\ &=& 21 \ ft \times 13.5 \ ft \\ &=& 283.5 \ ft^2 \end{array}\end{align*}$
::区域Box B=lxw=21 ftx13.5 ft=283.5 ft2

$\begin{aligned} \begin{array}{rcl} A r e a_{B o x C} & = & l \times w \\ = & 18 f t \times 27 f t \\ = & 486 f t^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} Area_{Box \ C} &=& l \times w \\ &=& 18 \ ft \times 27 \ ft \\ &=& 486 \ ft^2 \end{array}\end{align*}$
::区域Box C=lxw=18 ftx27 ft=486 ft2

Next, to find the probability that the ball will land in the box, just find the ratio of the area of box $\begin{align*}A\end{align*}$ to the area of the entire green side of the court.
::接下来,为了找到球在盒子里降落的概率, 只要找到A框面积与球场整个绿面面积的比率。

$\begin{aligned} \begin{array}{rcl} P (point in section) & = & \frac{area of favourable section}{total area} \\ P (ball lands in Box A) & = & \frac{area of Box A}{area Box A + area Box B + area Box C} \\ = & \frac{283.5}{283.5 + 283.5 + 486} \\ = & \frac{283.5}{1053} \\ = & 0.269 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P (\text{point in section}) &=& \frac{\text{area of favourable section}}{\text{total area}} \\ \\ P (\text{ball lands in Box}\ A) &=& \frac{\text{area of Box}\ A}{\text{area Box} \ A + \text{area Box} \ B + \text{area Box} \ C} \\ \\ &=& \frac{283.5}{283.5 + 283.5 + 486} \\ \\ &=& \frac{283.5}{1053} \\ \\ &=& 0.269 \end{array}\end{align*}$
::P(一节中的点点)=有利的区总面积面积P(方框A中的足球场)=方框A区框A+区框B+区框C=283.5283.5+283.5+283.5+486=283.51053=0.269

The answer is 0.269.
::答案是0.269。

There is a 0.269 or 26.9% chance the ball will land in the service box $\begin{align*}A\end{align*}$ .
::球在A号服务箱中降落的概率为0.269或26.9%。

You can also use geometric probability with circular regions.
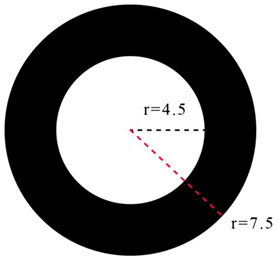
::您也可以使用圆形区域的几何概率。

Look at the image below. What is the probability that a random point selected would be in the white circle?
::查看下面的图像。选择的随机点在白圆中的概率是多少 ?

First, calculate the area of the inner white circle and the larger circle.
::首先,计算内白圆和大圆的面积。

$\begin{aligned} \begin{array}{rcl} A_{white circle} & = & π r^{2} \\ = & π (4.5)^{2} \\ = & π (20.25) \\ = & 63.6 i n^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{white circle}} &=& \pi r ^2 \\ &=& \pi (4.5)^2 \\ &=& \pi (20.25) \\ &=& 63.6 \ in^2 \end{array}\end{align*}$
::白圆r2(4.5)2(20.25)=63.6英寸2

$\begin{aligned} \begin{array}{rcl} A_{large circle} & = & π r^{2} \\ = & π (7.5)^{2} \\ = & π (56.25) \\ = & 176.7 i n^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{large circle}} &=& \pi r^2 \\ &=& \pi (7.5)^2 \\ &=& \pi (56.25) \\ &=& 176.7 \ in^2 \end{array}\end{align*}$
::大圆r2( 7.5) 2( 56. 25) = 176. 76. 7 英寸 2

Next, to find the probability that a random point will be located in the white circle, just find the ratio of the area of white circle to the area of the entire large circle.
::接下来,要找到一个随机点位于白圆的概率, 只需找到白圆区域与整个大圆区域的比例。

$\begin{aligned} \begin{array}{rcl} P (point in section) & = & \frac{area of favorable section}{total area} \\ P (point in white circle) & = & \frac{area of white circle}{total area} \\ = & \frac{63.6}{176.7} \\ = & 0.3599 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P (\text{point in section}) &=& \frac{\text{area of favorable section}}{\text{total area}} \\ P (\text{point in white circle}) &=& \frac{\text{area of white circle}}{\text{total area}} \\ &=& \frac{63.6}{176.7} \\ &=& 0.3599 \end{array}\end{align*}$
::P(部分中的点)=有利部分总面积的区域面积P(白圆中的点)=白圆总面积区域=63.6176.7=0.3599

The answer is 0.3599.
::答案是0.3599。

There is a 0.3599 or 36% chance the point selected will be in the white circle.
::选择的点在白圆上的可能性为0.3599或36%。

What if you wanted to find the probability of a point being randomly located in the black region.
::如果您想要找到点被随机定位在黑区的可能性,会怎样?

First, you know the area of the white circle is $\begin{align*}63.6 \ in^2\end{align*}$ and the total area of the circle is $\begin{align*}176.7 \ in^2\end{align*}$ . From these you can find the area of just the black region.
::首先,你知道白圆的面积是63.6英寸2,圆的总面积是176.7英寸2,从这些区域可以找到仅是黑色区域的区域。

$\begin{aligned} \begin{array}{rcl} A_{black region} & = & total area - A_{white circle} \\ = & 176.7 - 63.6 \\ = & 113.1 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{black region}} &=& \text{total area} - A_{\text{white circle}} \\ &=& 176.7 - 63.6 \\ &=& 113.1 \end{array}\end{align*}$
::Ablack地区=总面积-Awhite圆=176.7-63.6=113.1

Next, calculate the probability of a randomly selected point being found in the black region.
::下一步,计算在黑区域随机选择点的概率。

$\begin{aligned} \begin{array}{rcl} P (black region) & = & \frac{area of black region}{total area} \\ = & \frac{113.1}{176.7} \\ = & 0.64 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P(\text{black region}) &=& \frac{\text{area of black region}}{\text{total area}} \\ &=& \frac{113.1}{176.7} \\ &=& 0.64 \end{array}\end{align*}$
::P(黑区)=黑区总面积为113.1176.7=0.64的面积。

The answer is 0.64.
::答案是0.64

There is a 0.64 or 64% chance the point selected will be in the black region.
::选择的点在黑区的可能性为0.64或64%。

Notice that an easy way to find the $\begin{align*}P\end{align*}$ (black) is to recognize that $\begin{align*}P\end{align*}$ (black) and $\begin{align*}P\end{align*}$ (white) are complementary events .
::注意找到P(黑人)的简单方式是承认P(黑人)和P(白人)是互补事件。

The point must be either in the black area or the white area, so the two probabilities must add up to 100 percent.
::重点必须是在黑区或白色区,所以两种概率必须达到100%。

$\begin{aligned} \begin{array}{rcl} P (black) + P (white) & = & 100 % \\ P (black) + 36 % & = & 100 % \\ 64 % + 36 % & = & 100 % \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P (\text{black}) + P (\text{white}) &=& 100\% \\ P (\text{black}) + 36\% &=& 100\% \\ 64 \% + 36\% &=& 100\% \end{array}\end{align*}$
::P( black) +P( white) =100% P( black) + 36 @ 100% 64 @ 36 @ 100%

This is a way that you can check your work.
::这是一种你可以检查你工作的方法。

Notice that you will need to use the formula for the area of a circle to determine geometric probability related to area.
::请注意,您需要使用圆区域公式来确定与区域有关的几何概率。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about the pipe for the bike trick. Emma’s dad was talking about building the pipe.
::早些时候,有人给了你一个自行车操纵的管道问题。艾玛的爸爸在谈论建造管道的问题。

First, the minimum size for the larger piece would be 7 feet. That would make the smaller piece 3 feet in length. Mark this off on your diagram.
::首先,大块的最小尺寸为 7 英尺。这将使小块的长度小到 3 英尺。在您的图表上标记此值。

Next, notice that the pipe can also break on the other side. This is shown in red. With 3 feet on either end, that leaves a 4 foot length in the center of the pipe.
::下一步请注意, 管道也可以在另一侧破裂。红色显示。两端有三英尺, 在管子中间留下四英尺长。

Then, think of the pipe as separate areas. The shaded areas show regions where one of the pieces will be greater than 7 feet in length. These are your favorable sections.
::然后,你把管子当作单独的区域。阴暗的区域显示其中一块块的长度将大于7英尺的区域。这些是你们的优美区段。

So the probability of breaking into a piece that is 7 feet in length or greater is:
::因此,破碎到一个长度为7英尺或以上的碎片的概率是:

$\begin{aligned} \begin{array}{rcl} P (> 7 f t) & = & \frac{length of favorable section}{total length} \\ = & \frac{3 f t + 3 f t}{10 f t} \\ = & \frac{6}{10} \\ = & \frac{3}{5} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P (> \ 7 \ ft) &=& \frac{\text{length of favorable section}}{\text{total length}} \\ &=& \frac{3 \ ft + 3 \ ft}{10 \ ft} \\ &=& \frac{6}{10} \\ &=& \frac{3}{5} \end{array}\end{align*}$
::P( > 7 平方英尺) = 有利的部分总长度= 3 平方英尺+3 平方英尺= 610平方英尺= 35

The answer is $\begin{align*}\frac{3}{5}\end{align*}$ .
::答案是35岁

The probability is $\begin{align*}\frac{3}{5}\end{align*}$ or 60% that one piece of the pipe will be 7 feet long or greater.
::概率是35或60% 管子的一块长7英尺或7英尺以上

Example 2
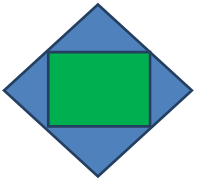
::例2

The Ultra Company displays this giant logo on a downtown billboard. The sides of the green rectangle measure 16 feet by 20 feet, while the sides of the blue square measure 28.2 feet. The logo is lit up by thousands of small high definition LCD pixels to light the area. What is the probability that one of the pixels will be burned out in the blue region?
::Ultra公司在市中心的一个广告牌上展示了这个巨大的标志。绿色矩形的两侧是16英尺乘20英尺,而蓝色方形的两侧是28.2英尺。这个标志被数千个小高定义的液晶像素点亮,以照亮这个区域。在蓝色区域燃烧像素的可能性有多大?

First, find the area of each section.
::首先,找到每一部分的面积。

$\begin{aligned} \begin{array}{rcl} A_{blue diamond} & = & s^{2} \\ = & (28.2)^{2} \\ = & 795.24 f t^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{blue diamond}} &=& s^2 \\ &=& (28.2)^2 \\ &=& 795.24 \ ft^2 \end{array}\end{align*}$
::Ablue 钻石=s2=(28.2)2=795.24平方英尺

$\begin{aligned} \begin{array}{rcl} A_{green rectangle} & = & l \times W \\ = & 16 \times 20 \\ = & 320 f t^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{green rectangle}} &=& l \times W \\ &=& 16 \times 20 \\ &=& 320 \ ft^2 \end{array}\end{align*}$
::绿矩形=lxW=16x20=320平方英尺2

Next, find the total area of the 4 equal-sized triangles. This area is equal to the area of the entire figure minus the central green rectangle.
::下一步, 找到 4 个等大小三角形的总面积。此区域等于整图区域, 减去中央绿色矩形。

$\begin{aligned} \begin{array}{rcl} A_{4 triangles} & = & A_{blue diamond} - A_{green diamond} \\ A_{4 triangles} & = & 795.24 - 320 \\ A_{4 triangles} & = & 475.24 f t^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{4 \ \text{triangles}} &=& A_{\text{blue diamond}} - A_{\text{green diamond}} \\ A_{4 \ \text{triangles}} &=& 795.24 - 320 \\ A_{4 \ \text{triangles}} &=& 475.24 \ ft^2 \end{array}\end{align*}$
::A4三角形=蓝色钻石-绿色钻石A4三角形=795.24-320A4三角形=475.24平方英尺

Then, find the probability that the next pixel will be burned out in the blue region.
::然后,找到下一个像素在蓝色区域被烧掉的概率。

$\begin{aligned} \begin{array}{rcl} P (blue region) & = & \frac{area of blue region}{total area} \\ = & \frac{475.24}{795.24} \\ = & 0.5976 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P(\text{blue region}) &=& \frac{\text{area of blue region}}{\text{total area}} \\ &=& \frac{475.24}{795.24} \\ &=& 0.5976 \end{array}\end{align*}$
::P(蓝色区域)=蓝色区域总面积=475 24795.24=0.5976

The answer is 0.5976.
::答案是0.5976。

There is a 0.5976 or 59.76% chance the next pixel will burn out in the blue region.
::下一个像素在蓝色区域燃烧的可能性是0.5976, 即59.76%。

Example 3
::例3

Which of the following geometric probabilities is impossible?
::以下哪些几何概率是不可能的?

0.95

1.25

0.00

1.00

Probabilities always lie between 0 and 1. You can have a 0% probability of snow in the desert and you can have a 100% probability that that there is a sun. Geometric probabilities cannot be greater 1 or be less than 0. Therefore answer b is incorrect.
::概率总是介于0到1之间。在沙漠中,雪的概率为0%,太阳的概率为100%。几何概率不能大于1或小于0。因此回答 b 不正确。

Example 4
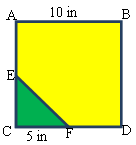
::例4

In the figure below, a point is selected at random in the square. What is the probability that this point will be found in the isosceles right triangle $\begin{align*}CEF\end{align*}$ ?
::在下图中,在正方形中随机选择一个点。在右三角的等分形 CEF 中发现此点的概率是多少?

First, calculate the area of the yellow square and the green triangle.
::首先,计算黄色方形和绿色三角形的区域。

$\begin{aligned} \begin{array}{rcl} A_{square} & = & s^{2} \\ = & (10)^{2} \\ = & 100 i n^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{square}} &=& s^2 \\ &=& (10)^2 \\ &=& 100 \ in^2 \end{array}\end{align*}$
::平方=s2=( 1010) 2=100 英寸2

$\begin{aligned} \begin{array}{rcl} A_{triangle} & = & \frac{1}{2} b h \\ = & \frac{1}{2} \times 5 \times 5 \\ = & \frac{1}{2} \times 25 \\ = & 12.5 i n^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} A_{\text{triangle}} &=& \frac{1}{2} \ bh \\ &=& \frac{1}{2} \times 5 \times 5 \\ &=& \frac{1}{2} \times 25 \\ &=& 12.5 \ in^2 \end{array}\end{align*}$
::矩形= 12 bh= 12 x5 x5= 12 x25= 12. 5 英寸 2

Next, to find the probability that a random point will be located in the triangle, just find the ratio of the area of triangle to the area of the square.
::下一步,要找到一个随机点位于三角形中的概率, 只需找到三角形区域与正方形区域的比例。

$\begin{aligned} \begin{array}{rcl} P (point in triangle) & = & \frac{area of triangle}{total area} \\ = & \frac{12.5}{100} \\ = & 0.125 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P (\text{point in triangle}) &=& \frac{\text{area of triangle}}{\text{total area}} \\ &=& \frac{12.5}{100} \\ &=& 0.125 \end{array}\end{align*}$
::P(三角中的点) = 三角总面积= 12. 5100=0. 125

The answer is 0.125
::答案是0.125

There is a 0.125 or 12.5% chance the point selected will be in the green triangle.
::选定点在绿色三角形中的概率为0.125或12.5%。

Example 5
::例5

A dart thrown at a line segment $\begin{align*}\overline{AC}\end{align*}$ can land at any point on it. What is the probability that it lands on $\begin{align*}\overline{BC}\end{align*}$ ? [Given $\begin{align*}a=19, b=9\end{align*}$ .]
::投向AC线段的飞镖随时可以降落它降落在BC的概率是多少? [给A=19,b=9]

First, find the length of $\begin{align*}AC\end{align*}$ .
::首先,找到空调的长度。

$\begin{aligned} \begin{array}{rcl} \bar{A C} & = & a + b \\ = & 9 + 19 \\ = & 28 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \overline{AC} &=& a+b \\ &=& 9 + 19 \\ &=& 28 \end{array}\end{align*}$
::AC a+b=9+19=28

Next, fill in the probability formula to find the ratio of the length of $\begin{align*}BC\end{align*}$ to the length of $\begin{align*}AC\end{align*}$ .
::其次,填入概率公式,以找到不列颠哥伦比亚与丙烷长度之比。

$\begin{aligned} \begin{array}{rcl} P (dart landing on \bar{B C}) & = & \frac{length of \bar{B C}}{length of \bar{A C}} \\ = & \frac{9}{28} \\ = & 0.321 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} P (\text{dart landing on} \ \overline{BC}) &=& \frac{\text{length of} \ \overline{BC}}{\text{length of} \ \overline{AC}} \\ &=& \frac{9}{28} \\ &=& 0.321 \end{array}\end{align*}$
::P(在BC上方着陆的电路)=BC 的长度=AC=928=0.321

The answer is 0.321.
::答案是0.321

There is a 0.321 or 32.1% chance the dart landing on $\begin{align*}\overline{BC}\end{align*}$ .
::在BC有0.321或32.1%的飞机降落机率

Review
::回顾

Draw diagrams to solve the problems.
::绘制解决问题的图表。

1. Geoff rode his bike along an 8 mile path and lost his cell phone at some random location somewhere along the way. What is the probability that Geoff’s phone dropped during the first mile of the path? (Assume there was an equal likelihood to loes the phone at any point along the path.)
::1. Geoff骑着自行车沿着一条8英里的路行驶,在沿途某个随机地点丢失了他的手机。 Geoff的手机在这条路第一英里时投下的可能性是多少? (假设在这条路的任何一点都有可能失去手机。 )

2. In the phone problem above, what is the probability that Geoff dropped his phone during the first mile or the last 2 miles?
::2. 在以上电话问题中,Geoff在第一英里或最后两英里时投下电话的可能性有多大?

3. In the phone problem above, Geoff searched from mile 4.5 to mile 7. What is the probability that he found the phone?
::3. 在以上电话问题中,Geoff从4.5英里到7英里进行了搜索。他找到电话的概率有多大?

4. In the phone problem above, a cell phone tower is located at mile 4 in the exact center of the path. The tower has a range of 2.75 miles. If Geoff uses a second cell phone to call his lost phone, what is the probability that the lost phone will ring?
::4. 在以上电话问题中,一个手机塔位于路径正中央4英里处,射程为2.75英里,如果Geoff用第二个手机打失的电话,丢失的电话响的几率有多大?

5. In the phone problem above, what range would the tower need to have to be sure that Geoff’s lost phone would ring?
::5. 在以上电话问题中,塔台需要多久才能确定Geoff丢失的电话会响?

Use this information on the football field to answer the following questions.
::使用有关足球场的信息回答下列问题。

A football field is 120 yards long –100 yards (green) plus two end zones (shown in red and blue) and 53 yards wide. The two hash mark lines that run across the center of the field are 13 yards apart and 20 yards from the sidelines. A pigeon flies over the stadium and lands at some random location on the football field. Round your answers to the nearest hundredths place for the following questions.
::足球场长120码 — — 100码(绿色)加上两端区域(红色和蓝色)和53码宽。横穿球场中心的两条散列线相隔13码,距离场外20码。一只鸽子飞过球场,在足球场上某个随机地点降落。以下为您最近的100个地方的答案。

6. What is the probability that the pigeon will land in one of the end zones?
::6. 鸽子在最终地带降落的可能性有多大?

7. What is the probability that the pigeon will land between the goal line and the 20 yard line on either side of the field?
::7. 鸽子在目标线和20码线之间降落的可能性有多大?

8. What is the probability that the pigeon will land within 5 yards of the 50-yard line?
::8. 鸽子在50码线5码内降落的可能性有多大?

9. What is the probability that the pigeon will land somewhere on the green part of the field?
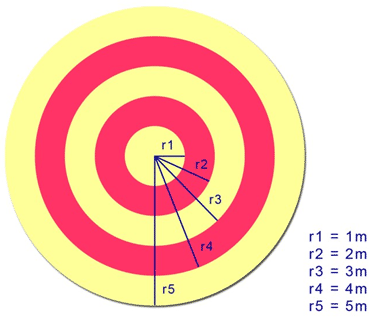
::9. 鸽子在田地绿地某处降落的可能性有多大?

Look at the diagram and then answer each question as it is related to geometric probabilities. Assume that any thrown dart will land somewhere within the circular area.
::看看图表,然后回答每一个问题,因为它与几何概率有关。假设任何投掷的飞镖都会降落在圆圈内某处。

10. The radius of circle 1 (the inner-most yellow circle) is 1 meter. Each radius thereafter increases by 1 m, as shown. What is the probability of a randomly thrown dart landing on circle 1?
::10. 圆1的半径为1米,如图所示,每一半径其后增加1米,任意投射的飞镖在圆1上着陆的概率是多少?

11. What is the probability that the dart will land in circle 2?
::11. 飞镖在第2圈降落的可能性有多大?

12. What is the probability that the dart will land in circle 3?
::12. 飞镖在第3圈降落的可能性有多大?

13. What is the probability that the dart will land in circle 4?
::13. 飞镖在第4圈降落的可能性有多大?

14. What is the probability that the dart will land in circle 5?
::14. 飞镖在第5圈降落的可能性有多大?

15. What is the probability that the dart will land in a yellow area?
::15. 飞镖在黄色区域降落的可能性有多大?

16. What is the probability that the dart will land in a red area?
::16. 飞镖在红色区域降落的可能性有多大?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

常规

理解几何概率

Geometric Probability ::几何概率

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Geometric Probability
::几何概率

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源