课程： 12.7 倍数单体 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节乘数单数

折叠展开
乘数单数
Jenny was trying out for the junior Math Olympiad at her school. She was doing very well until the judges gave her the following question to multiply.
::珍妮在学校试读小数学奥林匹亚

$\begin{aligned} (6 y^{3}) (8 y^{5}) (- 1 x y) \end{aligned}$

:6y3)(8y5)(-1xy)

Jenny was so confused by the question that she asked the judges to mark that question as her free pass. Can you help Jenny figure out the answer to her free pass question?
::珍妮被一个问题迷惑了,她要求法官将这个问题标记为她的免费通行证。你能帮助珍妮找出她免费通行证问题的答案吗?

In this concept, you will learn to multiply monomials.
::在这个概念中,你会学会乘以单子体。

Multiplying Monomials
::乘数单数

The parts of a term play a major role in multiplying monomials correctly.
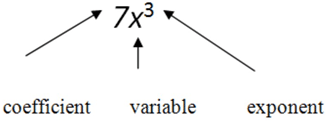
::术语中的某些部分在正确增加单项数字方面起着主要作用。

In the monomial above, the 7 is called the coefficient , the $\begin{aligned} x \end{aligned}$ is the variable , and the 3 is the exponent .
::在以上单项中,7项称为系数,x项为变量,3项为指数。

You can say that the monomial $\begin{aligned} 7 x^{3} \end{aligned}$ has a power of 3 or is to the 3 ^rd power.
::你可以说单体7x3 具有3或3的威力。

If there is no visible coefficient in front of the variable, then the coefficient is an unwritten 1. You could write “ $\begin{aligned} 1 x \end{aligned}$ ” but it is not necessary. Similarly, if there is no exponent on a coefficient or variable, then you can think of it as having an unwritten exponent of 1. So 7 could be written as 7 ¹ . The constant 7 then, is to the 1 ^st power.
::如果变量前面没有可见的系数,那么该系数就是一个不成文的系数1, 你可以写“ 1x ” , 但不必要。同样, 如果系数或变量上没有指数, 那么你可以把它视为有1的未写指数。所以, 7 可以写为71。那么, 常数 7 是对第一权力的。

Also, the exponent is applied to the constant, variable, or quantity that is directly to its left. That value is called the base . In the monomial above, the base is $\begin{aligned} x \end{aligned}$ . The exponent, in this case, is not applied to the 7 because it is not directly to the left of the exponent.
::此外,引号适用于其左侧的常数、可变数或数量。该值称为基数。在以上单数中,基数为x。在此情况下,引号不适用于7,因为它不是直接适用于指数左侧。

What is the exponent ? It’s a way of writing many multiplications in a simpler way. In the monomial above, $\begin{aligned} 7 x^{3} \end{aligned}$ , the 3 indicates that the variable $\begin{aligned} x \end{aligned}$ is multiplied by itself three times.
::引言是什么? 它是一种以简单的方式写出许多乘法的方式。在以上单数中, 7x3 3 表示变量 x 本身乘以三次。

$\begin{aligned} 7 x^{3} = 7 \cdot x \cdot x \cdot x \end{aligned}$

::7x3=7xxxxxxxxxxxx

When all of the multiplications are written out instead of using the exponent, it is called the expanded form . Imagine if the exponent were greater, like $\begin{aligned} 7 x^{27} \end{aligned}$ it would certainly take a lot of time, effort and space to write this in expanded form.
::当所有的乘数被写出来而不是使用引号时,它被称为扩展形式。想象一下如果引数更大, 比如 7x27 , 那么用扩展形式写它肯定需要很多的时间、精力和空间。

$\begin{aligned} 7 x^{27} = 7 \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \end{aligned}$

::7x27 = 7x27= 7xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx*xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

The exponent is truly valuable!
::推手是真正有价值的!

Let’s look at how to write an expression out into expanded form.
::让我们看看如何将表达方式写成扩展形式。

$\begin{aligned} (7 x^{3}) (4 x^{5}) = (7 \cdot x \cdot x \cdot x) (4 \cdot x \cdot x \cdot x \cdot x \cdot x) \end{aligned}$

:7x3)(4x5)=(7xxxxxx)(4xxxxxxxxxxxxxxxxx)

The expression has been written in expanded form.
::此表达式已以扩展格式写入。

Next, use the commutative property of multiplication to change the order of the factors so that similar factors are next to each other.
::其次,使用乘法的通量属性改变因素的顺序,使相近的因素相邻。

$\begin{aligned} \begin{array}{rcl} (7 x^{3}) (4 x^{5}) & = & (7 \cdot x \cdot x \cdot x) (4 \cdot x \cdot x \cdot x \cdot x \cdot x) \\ = & 7 \cdot 4 \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x Parentheses disappear \\ = & 28 x^{8} Multiply coefficients 7 and 4 \end{array} \end{aligned}$

:7x3)(4x5)=(7xxxxxxxx)(4xxxxxxxxxxx)=(7xxxxxxxxxxxxxxx))=(7xxxxxxxxxxxx))=(7xxxxxxxxxxxx)=(7xxxxxxxxx)=( 消失)=28x8

The exponent 8 serves as a shortcut for the variables.
::指数 8 作为变量的快捷键。

This question could also be done in another way. When multiplying expressions, multiply the coefficients and add the exponents of the same variables.
::这个问题也可以用另一种方式解决。当乘以表达式时, 乘以系数, 并添加相同变量的引言。

Let’s look at an example.
::让我们举个例子。

Multiply the monomials:
::乘以单数 :

$\begin{aligned} (7 x^{3}) (4 x^{5}) \end{aligned}$

:7x3)(4x5)

First, multiply the coefficients.
::首先,乘以系数。

$\begin{aligned} 7 \times 4 = 28 \end{aligned}$

Next, add the exponents.
::下加前列词。

$\begin{aligned} 3 + 5 = 8 \end{aligned}$

Then, put these together.
::然后把这些放在一起。

$\begin{aligned} (7 x^{3}) (4 x^{5}) = 28 x^{8} \end{aligned}$

:7x3)(4x5)=28x8

The answer is $\begin{aligned} 28 x^{8} \end{aligned}$ .
::答案是28x8。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Jenny and the free pass question. She couldn’t answer the question which involved multiplying monomials. How can she do this multiplication ?
::早些时候,有人给了你一个Jenny和自由通过问题的问题。她无法回答关于一模一样的乘法的问题。她怎么能做这种乘法呢?

Multiply the monomials:
::乘以单数 :

$\begin{aligned} (6 y^{3}) (8 y^{5}) (- 1 x y) \end{aligned}$

:6y3)(8y5)(-1xy)

First, multiply the three coefficients.
::首先,乘以三个系数。

$\begin{aligned} 6 \times 8 \times - 1 = - 48 \end{aligned}$

Next, add the exponents. Only add the exponents of $\begin{aligned} y \end{aligned}$ since this is the only common variable.
::下一步,添加引言。只添加 y 的引言,因为这是唯一的共同变量。

$\begin{aligned} 3 + 5 + 1 = 9 \end{aligned}$

Then, put these together.
::然后把这些放在一起。

$\begin{aligned} (6 y^{3}) (8 y^{5}) (- 1 x y) = - 48 y^{9} x \end{aligned}$

:6y3)(8y5)(-1xy)48y9x

The answer is $\begin{aligned} - 48 y^{9} x \end{aligned}$ .
::答案是 - 48y9x

Example 2
::例2

Multiply the following monomials:
$\begin{aligned} (- 6 x^{3}) (8 y^{5}) \end{aligned}$

::乘以下列单数-6x3)(8y5)

First, multiply the coefficients.
::首先,乘以系数。

$\begin{aligned} - 6 \times 8 = - 48 \end{aligned}$

Next, since the variables are not the same, you simply combine them with the coefficient.
::其次,由于变量不同,你只需将它们与系数结合起来即可。

$\begin{aligned} (- 6 x^{3}) (8 y^{5}) = - 48 x^{3} y^{5} \end{aligned}$

:- 6x3 (8y5) 48x3y5)

The answer is $\begin{aligned} - 48 x^{3} y^{5} \end{aligned}$ .
::答案是- 48x3y5。

Example 3
::例3

Multiply the following monomials:
::乘以下列单数:

$\begin{aligned} (6 x^{2}) (4 x^{4}) \end{aligned}$

:6x2)(4x4)

First, multiply the coefficients.
::首先,乘以系数。

$\begin{aligned} 6 \times 4 = 24 \end{aligned}$

Next, add the exponents.
::下加前列词。

$\begin{aligned} 2 + 4 = 6 \end{aligned}$

Then, put these together.
::然后把这些放在一起。

$\begin{aligned} (6 x^{2}) (4 x^{4}) = 24 x^{6} \end{aligned}$

:6x2)(4x4)=24x6

The answer is $\begin{aligned} 24 x^{6} \end{aligned}$ .
::答案是24x6

Example 4
::例4

Multiply the monomials:
::乘以单数 :

$\begin{aligned} (2 x^{3}) (4 x^{9}) \end{aligned}$

:2x3)(4x9)

First, multiply the coefficients.
::首先,乘以系数。

$\begin{aligned} 2 \times 4 = 8 \end{aligned}$

Next, add the exponents.
::下加前列词。

$\begin{aligned} 3 + 9 = 12 \end{aligned}$

Then, put these together.
::然后把这些放在一起。

$\begin{aligned} (2 x^{3}) (4 x^{9}) = 8 x^{12} \end{aligned}$

:2x3)(4x9)=8x12

The answer is $\begin{aligned} 8 x^{12} \end{aligned}$ .
::答案是8x12

Example 5
::例5

Multiply the monomials:
::乘以单数 :

$\begin{aligned} (6 y^{3}) (8 y^{5}) \end{aligned}$

:6y3(8y5))

First, multiply the coefficients.
::首先,乘以系数。

$\begin{aligned} 6 \times 8 = 48 \end{aligned}$

Next, add the exponents.
::下加前列词。

$\begin{aligned} 3 + 5 = 8 \end{aligned}$

Then, put these together.
::然后把这些放在一起。

$\begin{aligned} (6 y^{3}) (8 y^{5}) = 48 x^{8} \end{aligned}$

:6y3(8y-5)=48x8

The answer is $\begin{aligned} 48 x^{8} \end{aligned}$ .
::答案是48x8。

Review
::回顾

Multiply the following monomials.
::乘以下列单数。

$\begin{aligned} (5 x) (6 x y) \end{aligned}$
:5x( 6xy))

$\begin{aligned} (5 x^{2}) (- 6 x y) \end{aligned}$
:5x2)(-6xy)

$\begin{aligned} (- 5 x^{2} y) (2 x y^{2}) \end{aligned}$
:-5x2y(2xy2))

$\begin{aligned} (- 5 x) (- 9 y z) \end{aligned}$
:-5x(--9yz))

$\begin{aligned} (18 x y) (2 x y^{2} z) \end{aligned}$
:18xy)(2xy2z)

$\begin{aligned} (2 y^{4}) (6 y^{5}) \end{aligned}$
:2y4)(6y5)

$\begin{aligned} (5 x^{3}) (- 5 x^{4} y^{3}) \end{aligned}$
:5x3)(-5x4y3)

$\begin{aligned} (- 2 y^{5}) (6 y^{3}) (2 y^{2}) \end{aligned}$
:-2y5)(6y3)(2y2)

$\begin{aligned} (5 x y) (- 2 x y) (- x^{2} y^{2}) \end{aligned}$
:5xy)(-2xy)(-x2y2)

$\begin{aligned} (2 a b) (6 a b) (- 4 a b) \end{aligned}$
:2ab)(6ab)(-4ab)

$\begin{aligned} 7 x (6 x y) \end{aligned}$
::7x( 6xy)

$\begin{aligned} (15 x^{2}) (- 10 x^{3}) \end{aligned}$
:15x2)(-10x3)

$\begin{aligned} (5 x) (6 x y) (- 9 x y^{5}) \end{aligned}$
:5x6xy(-9xy5))

$\begin{aligned} (- 2 x^{3}) (- 4 x y) (- 5 x^{2} y^{4}) \end{aligned}$
:-2x3)(-4xy)(-5x2y4)

$\begin{aligned} (- 4 a b c) (- 8 a) (- 4 c) (d^{2}) \end{aligned}$
:-4abc)(-8a)(-4c)(d2)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

常规

乘数单数

Multiplying Monomials ::乘数单数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Multiplying Monomials
::乘数单数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源