课程： 12.13 理解Parabolas等同

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

理解Parabolas的等同

This parabola was created from an equation . What was the equation?
::这个抛物线是方程式创造出来的方程式是什么?

In this concept, you will learn to understand the equation of a parabola.
::在这一概念中,你会学会理解抛物线的方程式。

Parabolas
::抛物体

A parabola is a U-shaped graph.Equations with the ‘ $\begin{aligned} x \end{aligned}$ ’ variable raised to the 2 ^nd power are called quadratic equations and their graphs are always parabolas.
::抛物线是一个 U 形状的图形。以 `x ' 变量升至 2 次功率的等式被称为二次方程, 其图形总是 parapolas 。

Here is a quadratic equation .
::这里有一个二次方程。

\begin{aligned} y = x^{2} - 2 \end{aligned}

::y=x2-2

The graph of a parabola can change position, direction, and width based on the coefficients of $\begin{aligned} x^{2} \end{aligned}$ and $\begin{aligned} x \end{aligned}$ as well as the constant . Because those pieces of the equation are so important, you name them in what is called the standard form .
::抛物线的图形可以根据 x2 和 x 的系数以及常数来改变位置、方向和宽度。因为方程式中的这些部分如此重要, 您在标准格式中给它们命名。

Standard form of a quadratic equation: $\begin{aligned} y = a x^{2} + b x + c \end{aligned}$ (where ‘ $\begin{aligned} a \end{aligned}$ ’ cannot be zero). Notice that ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} b \end{aligned}$ ’ are coefficients and can be either positive or negative. The value of ‘ $\begin{aligned} c \end{aligned}$ ’ is a constant. All of these values affect the parabola that is graphed.
::二次方程的标准形式 : y= ax2+bx+c (其中`a ' 不能为零 ) 。请注意, `a ' 和`b ' 是系数,可以是正数,也可以是负数。 `c ' 的价值是一个常数。所有这些数值都会影响所绘制的抛物线。

Once again, the ‘ $\begin{aligned} a \end{aligned}$ ’ value can predict two things:
::A值可以预测两件事:

1. how wide the graph will be
::1. 图表的宽度

Generally speaking, the further the ‘ $\begin{aligned} a \end{aligned}$ ’ value is from zero, the narrower the graph; the closer the ‘ $\begin{aligned} a \end{aligned}$ ’ value is to zero, the wider the graph.
::一般说来, " a " 值越远来自零,越窄的图形; " a " 值越近于零,该图就越大。

2. if the graph opens upward or downward.
::2. 如果图表向上或向下开放。

A positive value of ‘ $\begin{aligned} a \end{aligned}$ ’ will give a graph that opens upwards while a negative value of ‘ $\begin{aligned} a \end{aligned}$ ’ will give a graph that opens downwards.
::“a”的正值将给出一个向上打开的图表,而“a”的负值将给出一个向下打开的图表。

What about the ‘ $\begin{aligned} b \end{aligned}$ ’ value?
::B 值如何?

All of the parabolas are symmetrical—they are the same on both sides, as if they were reflected on a mirror that were right down the middle of the graph. This reflection line is called the axis of . The ‘ $\begin{aligned} b \end{aligned}$ ’ value helps us to predict the axis of symmetry.
::所有抛光线都是对称的——两侧都是一样的,好像它们被反射到一面正下方的镜子上。这个反射线被称为 . 轴。 `b ' 值帮助我们预测对称轴。

Finally, the $\begin{aligned} c \end{aligned}$ value, determines the $\begin{aligned} y \end{aligned}$ - intercept of the graph—it tells where the graph will cross the $\begin{aligned} y \end{aligned}$ -axis. When the $\begin{aligned} c \end{aligned}$ value was 3, the graph crossed the $\begin{aligned} y \end{aligned}$ -axis at 3.
::最后, c 值, 确定图形的 y 界面- 它会显示图形要横过 y 轴的位置。当 c 值为 3 时, 图形会跨过 y 轴 3 。

Let’s look at some graphs.
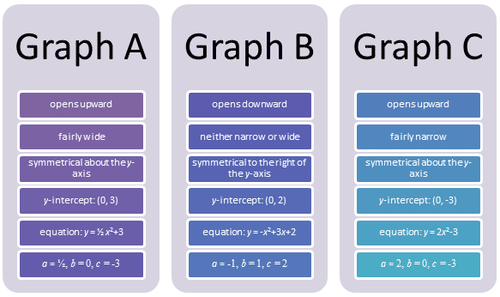
::让我们看看一些图表。

Looking at these graphs, and knowing what the $\begin{aligned} a, b \end{aligned}$ and $\begin{aligned} c \end{aligned}$ values of the quadratic equation represent, will help to determine the equation of the graph. Here is a chart to help you understand what you can determine by these graphs.
::查看这些图表,并了解四方形的a、b和c值,将有助于确定图形的方程。这里是一张图表,帮助您了解这些图表可以确定什么。

Now you can see how the graphs of each equation provide you with information.
::现在你可以看到每个方程式的图形如何为您提供信息。

You have learned to write linear equations based on linear graphs, you can also find a quadratic equation by using the parabola.
::您已经学会了根据线性图形撰写线性方程式, 您也可以通过使用 parbola 找到二次方程式。

You know that the ‘ $\begin{aligned} a \end{aligned}$ ’ value tells if the graph goes upward or downward. So, if the graph goes downward, the ‘ $\begin{aligned} a \end{aligned}$ ’ value must be negative. If the graph opens upward, the ‘ $\begin{aligned} a \end{aligned}$ ’ value must be positive.
::你知道“a”值表示图表向上还是向下。因此,如果图表向下,“a”值必须是负值。如果图表向上打开,“a”值必须是正值。

You also know that the ‘ $\begin{aligned} c \end{aligned}$ ’ value tells you the $\begin{aligned} y \end{aligned}$ -intercept on the graph. So, if you know the $\begin{aligned} y \end{aligned}$ -intercept, then you know the ‘ $\begin{aligned} c \end{aligned}$ ’ value.
::您也知道“ c” 值告诉您图形上的 Y 拦截。所以, 如果您知道 y 拦截 , 那么您就会知道 “ c” 值。

If you have a graph, then you can also work backwards. In other words, you can fill in a t-table using the points you see on the graph. Then, by looking for a pattern in the t-table, you can derive the equation.
::如果您有一个图表, 那么您也可以向后工作。换句话说, 您可以使用图表上显示的点填入一个t- 表格。然后, 通过在t- 表格中查找一个图案, 您可以从中得出公式。

Let’s look at an example.
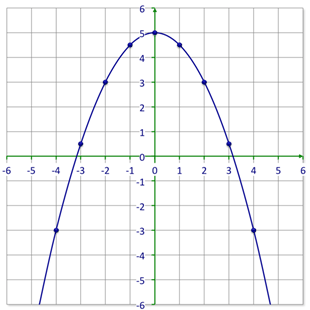
::让我们举个例子。

Write the equation for the given graph.
::写入给定图形的方程式。

First, start with what you know about the values of ‘ $\begin{aligned} a \end{aligned}$ ’ and ‘ $\begin{aligned} c \end{aligned}$ ’.
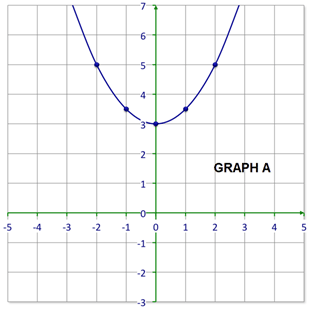
::首先,首先从你所知道的“a”和“c”的价值观开始。

$\begin{aligned} a \end{aligned}$ : Graph opens downward so $\begin{aligned} a < 0 \end{aligned}$ .
::a: 图表向下打开,以 < 0。

$\begin{aligned} c \end{aligned}$ : The $\begin{aligned} y \end{aligned}$ -intercept is (0, 3) so $\begin{aligned} c = 3 \end{aligned}$ .
::c: Y 界面是 (0, 3) so c=3。

Next, construct a table of values from the graph.
::下一步,从图表中构建一个数值表。

$\begin{aligned} x \end{aligned}$	$\begin{aligned} y \end{aligned}$
-2	-1
-1	2
0	3
1	2
2	-1

Then, put what you know into the standard form of the quadratic equation. Since the graph goes over one and down 1, you know that $\begin{aligned} a = - 1 \end{aligned}$ .
::然后,将你所知道的放入二次方程的标准形式。既然图表超过1和1,你知道A+1。

\begin{aligned} \begin{array}{rcl} y & = & a x^{2} + b x + c \\ y & = & - x^{2} + b x + 3 \end{array} \end{aligned}

::y=ax2+bx+cyx2+bx+3 y=ax2+bx+3

Then, test a point on the graph to find the value of $\begin{aligned} b \end{aligned}$ .
::然后,在图形上测试一个点以找到 b 的值。

\begin{aligned} y = x^{2} + b x + 3 \end{aligned}

::y=x2+bx+3 y=x2+bx+3

Point: (-1, 2)
::点数-1,2)

\begin{aligned} \begin{array}{rcl} 2 & = & - (- 1)^{2} + b (- 1) + 3 \\ 2 & = & - 1 + - b + 3 \\ 2 & = & - b + 2 \\ b & = & 0 \end{array} \end{aligned}

::2(- 1) 2+b(-1)+3211b+32b+2b+2b=0

The answer is $\begin{aligned} y = - x^{2} + 3 \end{aligned}$ .
::答案是yx2+3。

Examples
::实例

Example 1
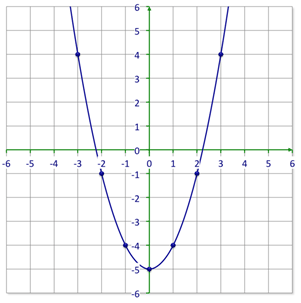
::例1

Earlier, you were given a problem about the parabola.
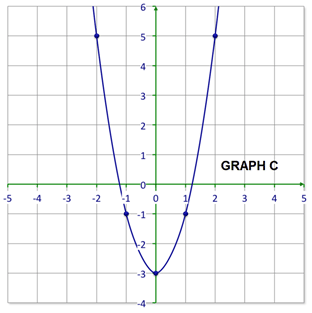
::早些时候,有人给了你一个关于抛物线的问题。

$\begin{aligned} a \end{aligned}$ : Graph opens upward so $\begin{aligned} a > 0 \end{aligned}$ .
::a: 图表向上打开,为 a>0。

$\begin{aligned} c \end{aligned}$ : The $\begin{aligned} y \end{aligned}$ -intercept is (0, 0) so $\begin{aligned} c = 0 \end{aligned}$ .
::c: Y 界面是 (0, 0) so c=0。

Next, construct a table of values from the graph.
::下一步,从图表中构建一个数值表。

$\begin{aligned} x \end{aligned}$	$\begin{aligned} y \end{aligned}$
-2	4
-1	1
0	0
1	1
2	4

Then, put what you know into the standard form of the quadratic equation. Since the graph goes over one and up 1, you know that $\begin{aligned} a = 1 \end{aligned}$ .
::然后,将你所知道的放入二次方程的标准形式。既然图表超过1和1,你知道A=1。

\begin{aligned} \begin{array}{rcl} y & = & a x^{2} + b x + c \\ y & = & x^{2} + b x \end{array} \end{aligned}

::y=ax2+bx+cy=x2+bx y=ax2+bx

Then, test a point on the graph to find the value of $\begin{aligned} b \end{aligned}$ .
::然后,在图形上测试一个点以找到 b 的值。

\begin{aligned} y = - x^{2} + b x \end{aligned}

::yx2+bx yx2+bx

Point: (-1, 1)
::点数-1,1)

\begin{aligned} \begin{array}{rcl} 1 & = & (- 1)^{2} + b (- 1) \\ 1 & = & 1 + - b \\ b & = & 0 \end{array} \end{aligned}

::1=(- 1) 2+b(- 1) 1=1bb=0

The answer is $\begin{aligned} y = x^{2} \end{aligned}$ .
::答案是y=x2。

Example 2
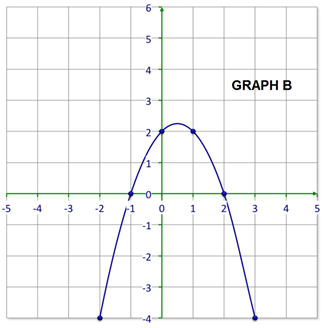
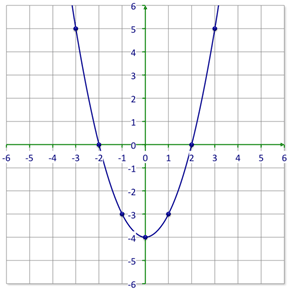
::例2

Figure out the equation for the following parabola.
::找出下列抛物线的方程。

$\begin{aligned} a \end{aligned}$ : Graph opens upward so $\begin{aligned} a > 0 \end{aligned}$ .
::a: 图表向上打开,为 a>0。

$\begin{aligned} c \end{aligned}$ : The $\begin{aligned} y \end{aligned}$ -intercept is (0, -4) so $\begin{aligned} c = - 4 \end{aligned}$ .
::c: Y 界面是 0, 4, so c4。

Next, construct a table of values from the graph.
::下一步,从图表中构建一个数值表。

$\begin{aligned} x \end{aligned}$	$\begin{aligned} y \end{aligned}$
-2	0
-1	-3
0	-4
1	-3
2	0

\begin{aligned} \begin{array}{rcl} y & = & a x^{2} + b x + c \\ y & = & x^{2} + b x - 4 \end{array} \end{aligned}

::y=ax2+bx+cy=x2+bx-4 y=ax2+bx+cy=x2+bx-4

Then, test a point on the graph to find the value of $\begin{aligned} b \end{aligned}$ .
::然后,在图形上测试一个点以找到 b 的值。

\begin{aligned} y = - x^{2} + b x - 4 \end{aligned}

::yx2+bx- 4 yx2+bx- 4

Point: (-1, -3)
::点数-1,-3)

\begin{aligned} \begin{array}{rcl} - 3 & = & (- 1)^{2} + b (- 1) - 4 \\ - 3 & = & 1 + - b - 4 \\ - 3 & = & - b - 3 \\ b & = & 0 \end{array} \end{aligned}

::- 3=(-1)2+b(-1)-4-3=1b-4-3-3b-3b=0

The answer is $\begin{aligned} y = x^{2} - 4 \end{aligned}$ .
::答案是y=x2 -4。

Example 3
::例3

If the $\begin{aligned} c \end{aligned}$ value is 4, where is the $\begin{aligned} y \end{aligned}$ -intercept of the graph?
::如果 c 值是 4 , 图形的 Y 界面在哪里 ?

If $\begin{aligned} c = 4 \end{aligned}$ , the $\begin{aligned} y \end{aligned}$ –intercept or the point where the curve crosses the $\begin{aligned} y \end{aligned}$ -axis is (0, 4).
::如果 c= 4, y - interview 或曲线通过 y 轴的点 (0, 4) 。

Example 4
::例4

If the ‘ $\begin{aligned} a \end{aligned}$ ’ value is −3, will the parabola open upward or downward?
::如果`a ' 值为-3, 抛物线会向上或向下打开吗?

If $\begin{aligned} a < 0 \end{aligned}$ , then the graph opens downward so when $\begin{aligned} a = - 3 \end{aligned}$ , the graph will open downward.
::如果 a<0,则图形向下打开,当 a\\\\\3 时,图形向下打开。

Example 5
::例5

If the parabola opens upward, which value is positive $\begin{aligned} a, b \end{aligned}$ or $\begin{aligned} c \end{aligned}$ .
::如果抛物线向上打开,该值为正a、b或c。

When the graph opens upward or downward, the value of ‘ $\begin{aligned} a \end{aligned}$ ’ is affected. Therefore if the graph opens upward you know that ‘ $\begin{aligned} a \end{aligned}$ ’ is positive.
::当图表向上或向下打开时,“a”的值就会受到影响。因此,如果向上打开,您就会知道“a”是正数。

Review
::回顾

Answer the following questions about parabolas.
::回答下列关于parabolas的问题。

1. True or false. All parabolas are symmetrical.
::1. 真实的或虚假的,所有抛物线都是对称的。

2. True or false. The $\begin{aligned} y \end{aligned}$ intercept is the same as the $\begin{aligned} c \end{aligned}$ value.
::2. 真实或虚假。拦截y与c值相同。

3. A parabola with a positive squared value opens __________.
::3. 具有正正平方值的抛物线打开_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4. A parabola with a negative squared value opens __________.
::4. 负正方值的抛物线打开____________________________________________________________________________________________________________________________________________

5. What is the vertex of the parabola?
::5. 抛物线的顶部是什么?

6. True or false. A parabola always forms a U shape.
::6. 真实的或假的,抛物线总是形成U形。

7. True or false. The closer the $\begin{aligned} a \end{aligned}$ value is to zero the wider the parabola.
::7. 真实或虚假,值越接近零,抛物线越大。

8. True or false. The closer the $\begin{aligned} a \end{aligned}$ value is to zero the narrower the parabola.
::8. 真实的或虚假的,值越接近零,抛物线越窄。

9. True or false. The $\begin{aligned} b \end{aligned}$ value determines the axis of symmetry.
::9. 正确或虚假。b值决定对称轴。

10. What does the $\begin{aligned} c \end{aligned}$ value indicate?
::10. C值表示什么?

11. True or false. A linear equation will have a graph that is a parabola.
::11. 真实的或虚假的,线性方程将有一个图示,即抛物线。

12. True or false. A quadratic equation and a linear equation will have a similar graph.
::12. 真实或假方程式。二次方程式和线性方程式将有类似的图表。

Write the equations of the following graphs. Use the $\begin{aligned} a \end{aligned}$ and $\begin{aligned} c \end{aligned}$ values and a t-table to help you.
::写入下图的方程式。使用 a 和 c 值和 t 表格来帮助您。

13.

14.

15.

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

理解Parabolas的等同

Parabolas ::抛物体

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Parabolas
::抛物体

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源