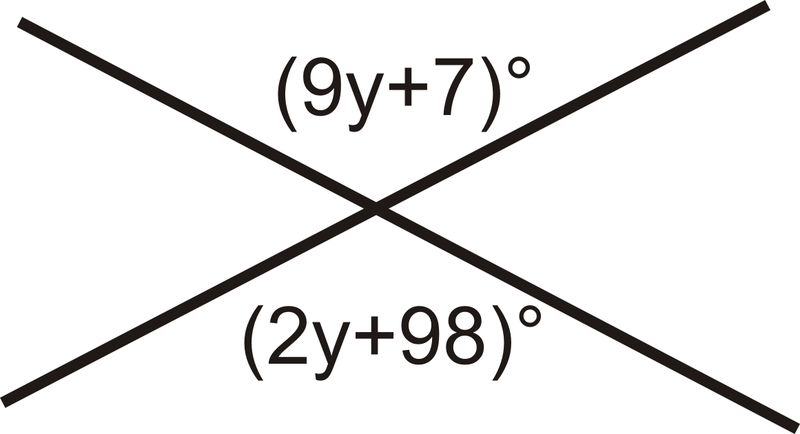Course: 1. 10 垂直角度 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 垂直角

Collapse Expand
垂直角
Vertical Angles
::垂直角

Vertical angles are two non- adjacent angles formed by intersecting lines . $\begin{aligned} ∠ 1 \end{aligned}$ and $\begin{aligned} ∠ 3 \end{aligned}$ are vertical angles and $\begin{aligned} ∠ 2 \end{aligned}$ and $\begin{aligned} ∠ 4 \end{aligned}$ are vertical angles.
::垂直角度是横交线形成的两个非相邻角度。% 1 和% 3 是垂直角度,% 2 和% 4 是垂直角度。

The Vertical Angles Theorem states that if two angles are vertical angles, then they are congruent .
::垂直角理论指出,如果两个角度是垂直角度,那么它们就是相同的。

What if you were given two angles of unknown size and were told they are vertical angles? How would you determine their angle measures?
::如果给您两个大小不明的角度,并被告知它们是垂直角度呢?您将如何确定它们的角度量度?

Examples
::实例

Example 1
::例1

Find the value of $\begin{aligned} x \end{aligned}$ .
::查找 x 的值。

Vertical angles are congruent, so set the angles equal to each other and solve for $\begin{aligned} x \end{aligned}$ .
::垂直角度是相容的, 所以设置对等角度, 并解析 x 。

$\begin{aligned} x + 16 & = 4 x - 5 \\ 3 x & = 21 \\ x & = 7^{\circ} \end{aligned}$

::x+16=4x-53x=21x=7=7

Example 2
::例2

Find the value of $\begin{aligned} y \end{aligned}$ .
::查找 y 的值。

Vertical angles are congruent, so set the angles equal to each other and solve for $\begin{aligned} y \end{aligned}$ .
::垂直角度是相容的, 所以设置对等的角度, 并为 y 求解。

$\begin{aligned} 9 y + 7 & = 2 y + 98 \\ 7 y & = 91 \\ y & = 13^{\circ} \end{aligned}$

::9+7=2y+987y=91y=13

Example 3
::例3

Find $\begin{aligned} m ∠ 1 \end{aligned}$ .
::找到 m1 。

$\begin{aligned} ∠ 1 \end{aligned}$ is vertical angles with $\begin{aligned} 18^{\circ} \end{aligned}$ , so $\begin{aligned} m ∠ 1 = 18^{\circ} \end{aligned}$ .
::1是垂直角度与 18 。所以m1 = 18 。

Example 4
::例4

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (4 x + 10)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (5 x + 2)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角和“ABC”=(4x+10)”和“mDEF=(5x+2)”,那么每个角度的量度是多少?

Vertical angles are congruent, so set the angles equal to each other and solve for $\begin{aligned} x \end{aligned}$ . Then go back to find the measure of each angle.
::垂直角度是相容的, 所以设置对等角度, 并解析 x。然后返回找到每个角度的量度。

$\begin{aligned} 4 x + 10 & = 5 x + 2 \\ x & = 8 \end{aligned}$

::4x+10=5x+2x=8

So, $\begin{aligned} m ∠ A B C = m ∠ D E F = (4 (8) + 10)^{\circ} = 42^{\circ} \end{aligned}$
::所以,mABC=mDEF=(4(8)+10)42

Example 5
::例5

True or false: vertical angles are always less than $\begin{aligned} 90^{\circ} \end{aligned}$ .
::真实或假的:垂直角度总是小于 90 。

This is false, you can have vertical angles that are more than $\begin{aligned} 90^{\circ} \end{aligned}$ . Vertical angles are less than $\begin{aligned} 180^{\circ} \end{aligned}$ .
::这是虚假的, 您可以有超过 90 的垂直角度。垂直角度小于 180 。

Review
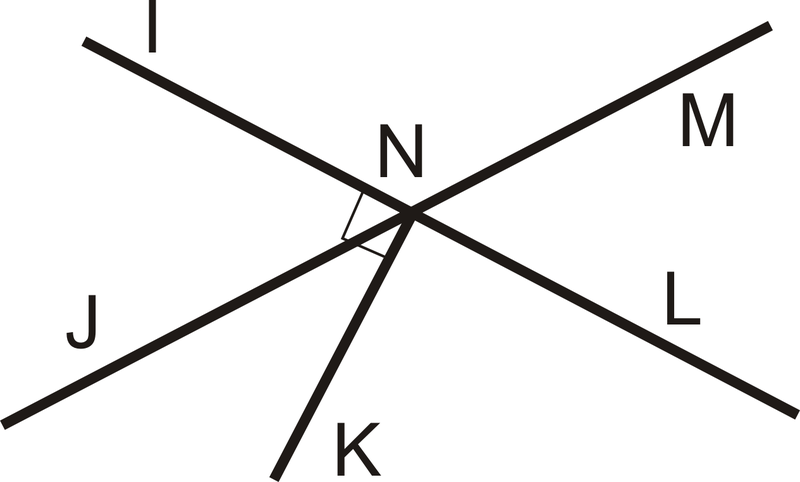
::回顾

Use the diagram below for exercises 1-2. Note that $\begin{aligned} \bar{N K} ⊥ \overset{\leftrightarrow}{I L} \end{aligned}$ .
::练习1-2使用下图。请注意 NK IL。

Name one pair of vertical angles.
::列出一对垂直角度。

If $\begin{aligned} m ∠ I N J = 63^{\circ} \end{aligned}$ , find $\begin{aligned} m ∠ M N L \end{aligned}$ .
::如果MINJ=63,找到MMNL。

For exercise 3, determine if the statement is true or false.
::对于第3项练习,确定该陈述是真实还是虚假。

Vertical angles have the same vertex.
::垂直角度具有相同的顶点。

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (9 x + 1)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (5 x + 29)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角度和“ABC”=(9x+1)”和“M”DEF=(5x+29),那么每个角度的量度是多少?

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (8 x + 2)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (2 x + 32)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角和“ABC”=(8x+2)”和“M”DEF=(2x+32)”,那么每个角的量度是多少?

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (x + 22)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (5 x + 2)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角和“ABC”=(x+22)”和“mDEF=(5x+2)”,那么每个角度的量度是多少?

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (3 x + 12)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (7 x)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角和“ABC”=(3x+12)”和“M”DEF=(7x)”,则每个角的量度是多少?

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (5 x + 2)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (x + 26)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角和“ABC”=(5x+2)”和“mDEF=(x+26)”,那么每个角度的量度是多少?

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (3 x + 1)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (2 x + 2)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角度和“ABC”=(3x+1)”和“mDEF=(2x+2)”,那么每个角度的量度是多少?

If $\begin{aligned} ∠ A B C \end{aligned}$ and $\begin{aligned} ∠ D E F \end{aligned}$ are vertical angles and $\begin{aligned} m ∠ A B C = (6 x - 3)^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ D E F = (5 x + 1)^{\circ} \end{aligned}$ , what is the measure of each angle?
::如果“ABC”和“DEF”是垂直角和“(6x-3)”和“(5x+1)”,那么每个角度的量度是多少?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

Section outline

General

垂直角

Vertical Angles ::垂直角

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Vertical Angles
::垂直角

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源