3.7 坐标平面的斜坡

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节坐标平面的斜坡

  折叠 展开

  坐标平面的斜坡

  播放段落

  Slope in the Coordinate Plane
  ::坐标平面的斜坡

  播放段落

  Recall from Algebra I that is the measure of the steepness of a line. Two points $\begin{array}{r}(x_1,y_1)\end{array}$ and $\begin{array}{r}(x_2,y_2)\end{array}$ have a slope of $\begin{array}{r}m=\frac{(y_2-y_1)}{(x_2-x_1)}\end{array}$ . You might have also learned slope as $\begin{array}{r}\frac{rise}{run}\end{array}$ . This is a great way to remember the formula . Also remember that if an equation is written in slope-intercept form , $\begin{array}{r}y=mx+b\end{array}$ , then $\begin{array}{r}m\end{array}$ is always the slope of the line.
  ::从代数 I 中回顾, 这是线的陡度 。 两点 (x1,y1) 和 (x2,y2) 具有 m= (y2-y1) (x2-x1) (x2) 的斜度, 您也可以将斜度作为正上线学习 。 这是记住公式的绝佳方法 。 还要记住, 如果公式以斜度- intercept 形式写成, y=mx+b, 那么 m 总是线的斜度 。

  播放段落

  Slopes can be positive, negative, zero, or undefined as shown in the pictures below:
  ::缩略语可以是正、负、零或未定义的,如下图所示:

  播放段落

  Positive:
  ::阳性:

  播放段落

  Negative:
  ::负:

  播放段落

  Zero:
  ::零:

  播放段落

  Undefined:
  ::未定义 :

  播放段落

  What if you were given the coordinates of two points? How would you determine the steepness of the line they form?
  ::假若你们获得两点的坐标,那末,你们怎么判定两点之间最陡峭的长度呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

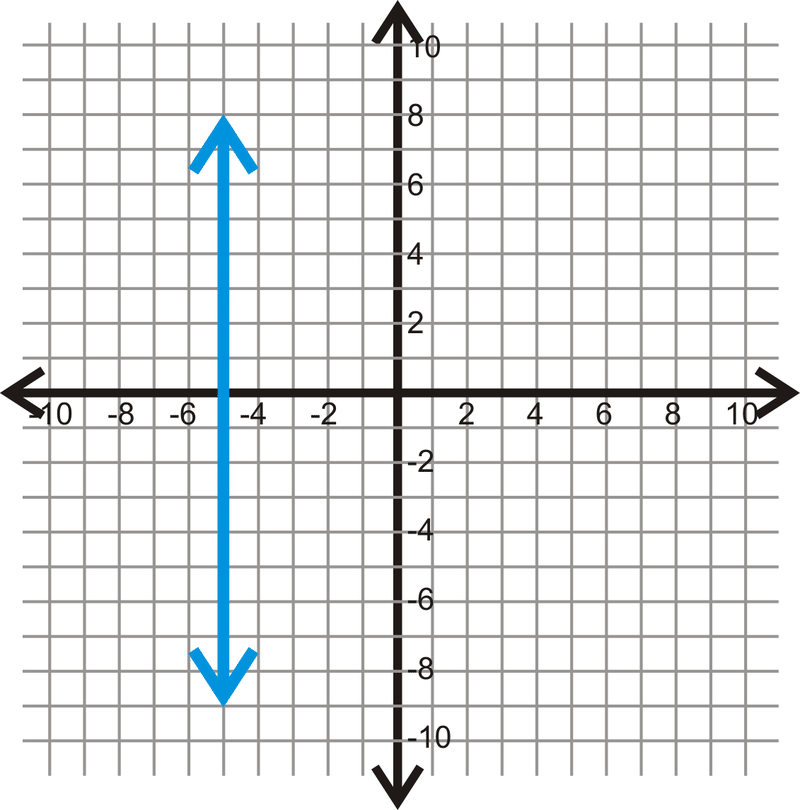
  播放段落

  What is the slope of the line through (3, 2) and (3, 6)?
  ::线的坡度是多少(3,2)和(3,6)?

  

  播放段落

  Use (3, 2) as $\begin{array}{r}(x_1,y_1)\end{array}$ and (3, 6) as $\begin{array}{r}(x_2,y_2)\end{array}$ .
  ::使用(3,2)为(11,y1),使用(3,6)为(12,y2)。

  播放段落

  $$\begin{array}{r}m=\frac{6-2}{3-3}=\frac{4}{0}=undefined\end{array}$$

  
  ::m=6 - 23 - 3=40=未定义

  播放段落

  The slope of this line is undefined, which means that it is a vertical line. Vertical lines always pass through the $\begin{array}{r}x-\end{array}$ axis. The $\begin{array}{r}x-\end{array}$ coordinate for both points is 3. So, the equation of this line is $\begin{array}{r}x=3\end{array}$ .
  ::此线的斜度未定义, 这意味着它是一条垂直线。 垂直线总是通过 x- 轴。 两个点的 x- 坐标是 3 。 因此, 此线的方程式是 x= 3 。

  播放段落

  Example 2
  ::例2

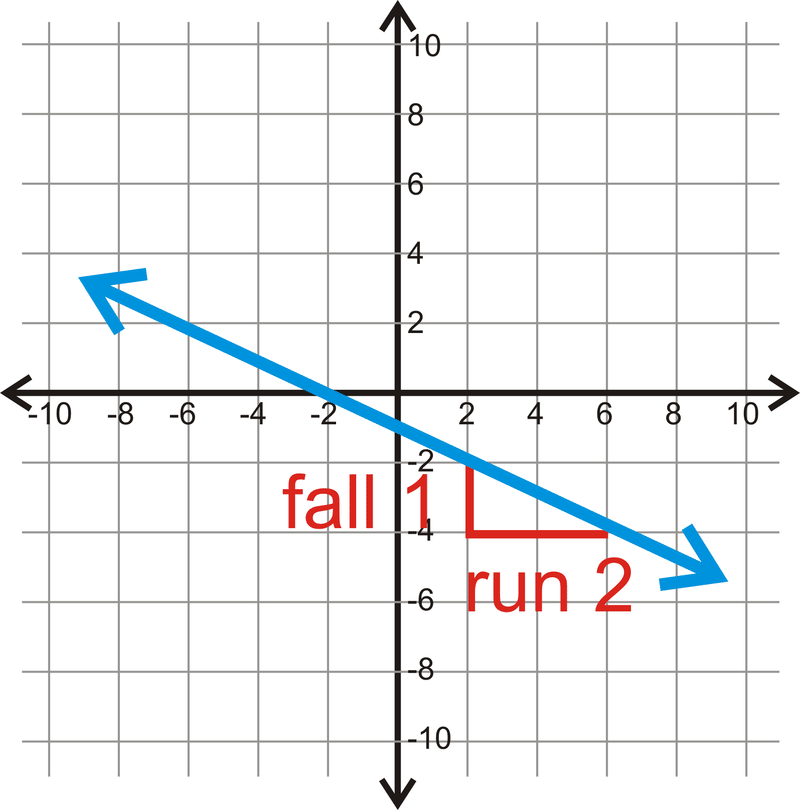
  播放段落

  Find the slope between (-5, 2) and (3, 4).
  ::在(5,2)和(3,4)之间找到斜坡。

  播放段落

  Use (-5, 2) as $\begin{array}{r}(x_1,y_1)\end{array}$ and (3, 4) as $\begin{array}{r}(x_2,y_2)\end{array}$ .
  ::将(-5,2)作为(x1,y1)和(3,4)作为(x2,y2)使用。

  播放段落

  $$\begin{array}{r}m=\frac{4-2}{3-(-5)}=\frac{2}{8}=\frac{1}{4}\end{array}$$

  
  ::m=4-23-(-5-5)=28=14

  播放段落

  Example 3
  ::例3

  播放段落

  What is the slope of the line through (2, 2) and (4, 6)?
  ::线的坡度是多少(2、2和4、6)?

  

  播放段落

  Use (2, 2) as $\begin{array}{r}(x_1,y_1)\end{array}$ and (4, 6) as $\begin{array}{r}(x_2,y_2)\end{array}$ .
  ::使用(2,2)为(x1,y1),使用(4,6)为(x2,y2)。

  播放段落

  $$\begin{array}{r}m=\frac{6-2}{4-2}=\frac{4}{2}=2\end{array}$$

  
  ::m=6-24-2=42=2

  播放段落

  Example 4
  ::例4

  播放段落

  Find the slope between (-8, 3) and (2, -2).
  ::在(8,3)和(2,2)之间找到斜坡。

  

  播放段落

  Use (-8, 3) as $\begin{array}{r}(x_1,y_1)\end{array}$ and (2, -2) as $\begin{array}{r}(x_2,y_2)\end{array}$ .
  ::使用(-8, 3)为(x1,y1),使用(2, 2)为(x2, y2)。

  播放段落

  $$\begin{array}{r}m=\frac{-2-3}{2-(-8)}=\frac{-5}{10}=-\frac{1}{2}\end{array}$$

  
  ::m2 - 32 - (-8) 510 - 12

  播放段落

  Example 5
  ::例5

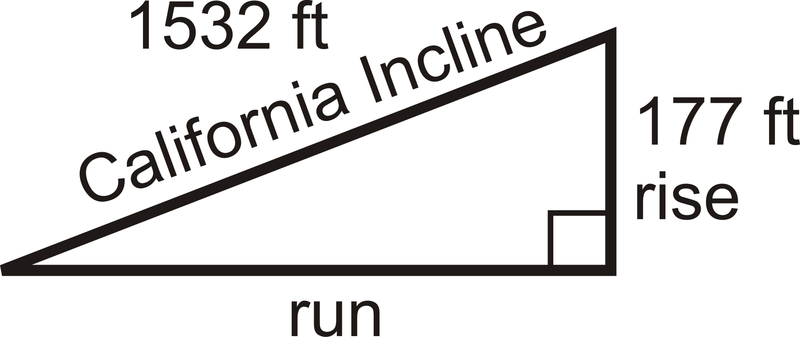
  播放段落

  The picture shown is the California Incline, a short road that connects Highway 1 with Santa Monica. The length of the road is 1532 feet and has an elevation of 177 feet. You may assume that the base of this incline is zero feet. Can you find the slope of the California Incline?
  ::显示的图片是加利福尼亚 Incline, 这条连接1号公路和圣莫尼卡的短路。 这条公路的长度是1532英尺, 高度是177英尺。 您可以假定这个Incline的底部是零英尺。 您能找到加利福尼亚 Incline的斜坡吗 ?

  

  播放段落

  In order to find the slope, we need to first find the horizontal distance in the triangle shown. This triangle represents the incline and the elevation. To find the horizontal distance, we need to use the Pythagorean Theorem (a concept you will be introduced to formally in a future lesson), $\begin{array}{r}{a}^2+b^2=c^2\end{array}$ , where $\begin{array}{r}c\end{array}$ is the hypotenuse .
  ::为了找到斜坡, 我们需要首先在显示的三角形中找到水平距离 。 此三角形代表直线和高度 。 要找到水平距离, 我们需要使用 Pytagorean Theorem( 您将在未来的课程中正式引入这个概念) , a2+b2=c2, 其中 c 是下限 。

  

  播放段落

  $$\begin{array}{rl}{177}^2+ru{n}^2& ={1532}^2\\ 31,329+ru{n}^2& =2,347,024\\ ru{n}^2& =2,315,695\\ run& \approx 1521.75\end{array}$$

  
  ::1772+run2=1532231 329+run2=2,347,024run2=2,315,695run*1521.75

  播放段落

  The slope is then $\begin{array}{r}\frac{177}{1521.75}\end{array}$ , which is roughly $\begin{array}{r}\frac{3}{25}\end{array}$ .
  ::斜坡为177 1521.75,大约为325。

  播放段落

  Review
  ::回顾

  播放段落

  Find the slope between the two given points.
  ::查找两个给定点之间的斜坡。

  播放段落
  1. (4, -1) and (-2, -3)
     :4,-1和2,3)
  播放段落
  2. (-9, 5) and (-6, 2)
     :9,5)和(6,2)
  播放段落
  3. (7, 2) and (-7, -2)
     :7、7、2和7、7、2)
  播放段落
  4. (-6, 0) and (-1, -10)
     :-6,0)和(-1,-10)
  播放段落
  5. (1, -2) and (3, 6)
     :1,2)和(3,6)
  播放段落
  6. (-4, 5) and (-4, -3)
     :-4、5和4)和(-4、3)
  播放段落
  7. (-2, 3) and (-2, -3)
     :-2,3和2,3)和(-2,3)
  播放段落
  8. (4, 1) and (7, 1)
     :第4、第1、第4、第1和第7、第1段)

  播放段落

  For 9-10, determine if the statement is true or false.
  ::9-10,确定声明是真实还是虚假。

  播放段落
  9. If you know the slope of a line you will know whether it is pointing up or down from left to right.
     ::如果你知道一条线的斜坡,你就会知道这条线是向上还是向下,从左到右。
  播放段落
  10. Vertical lines have a slope of zero.
      ::垂直线的斜坡为零。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。