4.9 HL三角汇合度

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节HL 三角汇合度

  折叠 展开

  HL 三角汇合度

  播放段落

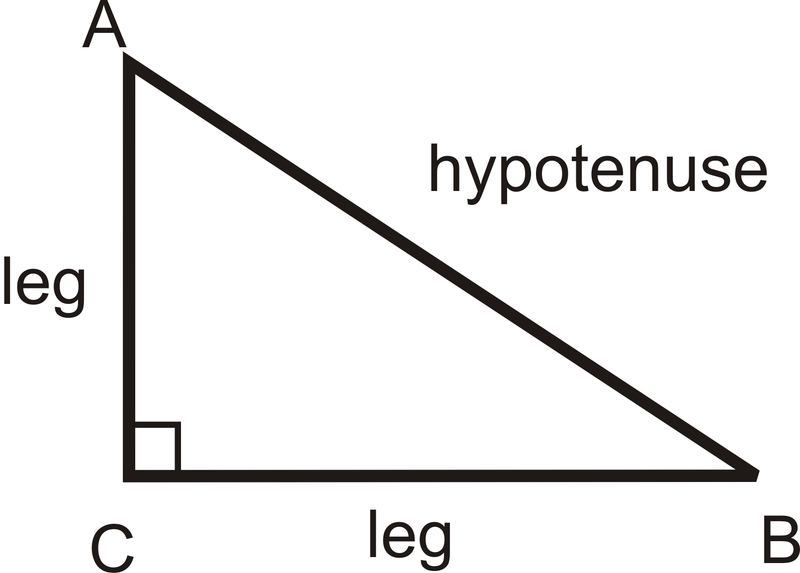
  Hypotenuse-Leg Congruence Theorem
  ::日均值 - Leg Congruence 定理

  播放段落

  If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. This is called the Hypotenuse-Leg (HL) Congruence Theorem . Note that it will only work for right triangles.
  ::如果一个右三角形的下限和腿与下限和腿与另一个右三角形的下限和腿相匹配,则两个三角形是相匹配的。这称为“HL 相容理论 ” 。 请注意, 它只对右三角形有效 。

  播放段落

  If $\begin{array}{r}\mathrm{△}ABC\end{array}$ and $\begin{array}{r}\mathrm{△}XYZ\end{array}$ are both right triangles and $\begin{array}{r}\overline{AB}\cong \overline{XY}\end{array}$ and $\begin{array}{r}\overline{BC}\cong \overline{YZ}\end{array}$ then $\begin{array}{r}\mathrm{△}ABC\cong \mathrm{△}XYZ\end{array}$ .
  ::如果ABC和XYZ是右三角 ABXY和BCYZ,然后ABCXYZ。

  

  播放段落

  What if you were given two right triangles and provided with only the measure of their hypotenuses and one of their legs ? How could you determine if the two right triangles were congruent?
  ::假若你们获得两个右三角形,而你们得享受两个右三角形的体积,和他们的一条腿的体积,你们怎能断定两个右三角形是否一致呢?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Fill in the blanks in the proof below.
  ::填充以下证据中的空白。

  播放段落

  Given :
  ::参照:

  播放段落

  $\begin{array}{r}\overline{SV}\perp \overline{WU}\end{array}$
  ::SV WWW( SV )

  播放段落

  $\begin{array}{r}T\end{array}$ is the midpoint of $\begin{array}{r}\overline{SV}\end{array}$ and $\begin{array}{r}\overline{WU}\end{array}$
  ::T 是SV和WU的中点

  播放段落

  Prove : $\begin{array}{r}\overline{WS}\cong \overline{UV}\end{array}$
  ::证明:

  

  Statement	Reason
  1.	1.
  2. $\begin{array}{r}\mathrm{\angle }STW\end{array}$ and $\begin{array}{r}\mathrm{\angle }UTV\end{array}$ are right angles	2.
  3.	3.
  4. $\begin{array}{r}\overline{ST}\cong \overline{TV},\overline{WT}\cong \overline{TU}\end{array}$	4.
  5. $\begin{array}{r}\mathrm{△}STW\cong \mathrm{△}UTV\end{array}$	5.
  6. $\begin{array}{r}\overline{WS}\cong \overline{UV}\end{array}$	6.

  Statement	Reason
  1. $\begin{array}{r}\overline{SV}\perp \overline{WU}\end{array}$	1. Given
  2. $\begin{array}{r}\mathrm{\angle }STW\end{array}$ and $\begin{array}{r}\mathrm{\angle }UTV\end{array}$ are right angles	2. Definition of perpendicular lines .
  3. $\begin{array}{r}T\end{array}$ is the midpoint of $\begin{array}{r}\overline{SV}\end{array}$ and $\begin{array}{r}\overline{WU}\end{array}$	3. Given
  4. $\begin{array}{r}\overline{ST}\cong \overline{TV},\overline{WT}\cong \overline{TU}\end{array}$	4. Definition of midpoint
  5. $\begin{array}{r}\mathrm{△}STW\cong \mathrm{△}UTV\end{array}$	5.
  6. $\begin{array}{r}\overline{WS}\cong \overline{UV}\end{array}$	6.

  播放段落

  Note that even though these were right triangles, we did not use the congruence shortcut because we were not originally given that the two hypotenuses were congruent. The SAS congruence shortcut was quicker in this case.
  ::请注意,尽管这些是正确的三角形,但我们并没有使用一致的捷径,因为我们最初没有被告知这两个次元是一致的。 在这种情况下,SAS的一致捷径更快。

  播放段落

  Example 2
  ::例2

  播放段落

  Explain why the HL Congruence shortcut works.
  ::解释为什么HL Congruence捷径有效。

  播放段落

  , which says, for any right triangle, this equation is true:
  ::也就是说,对于任何右三角形来说,这个方程式是真实的:

  播放段落

  $$\begin{array}{r}(leg{)}^2+(leg{)}^2=(hypotenuse{)}^2\end{array}$$

  
  :leg)2+(leg)2=(抵押)2

  

  播放段落

  What this means is that if you are given two sides of a right triangle, you can always find the third. Therefore, if you know two sides of a right triangle are congruent to two sides of another right triangle, then you can conclude that the third sides are also congruent. If three pairs of sides are congruent, then we know the triangles are congruent by .
  ::这意味着,如果给您右三角两面,您总能找到第三面。因此,如果您知道右三角两面与右三角两面是一致的,那么您可以得出结论,三面也是一致的。如果三对是一致的,那么我们就知道三角是一致的。

  播放段落

  Example 3
  ::例3

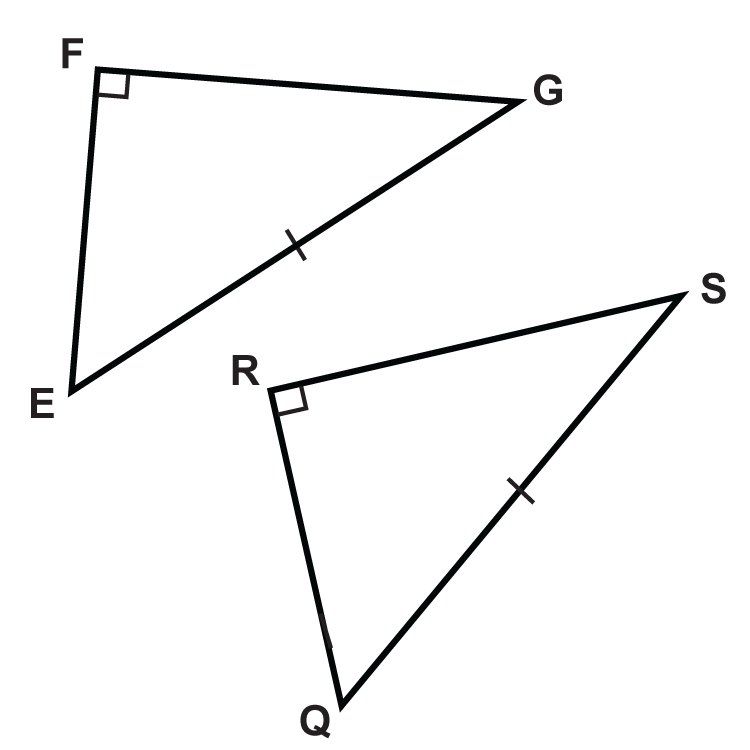
  播放段落

  What additional information would you need to prove that these two triangles were congruent using the HL Theorem?
  ::您需要哪些补充信息来证明这两个三角形使用 HL 定理是一致的 ?

  

  播放段落

  For HL, you need the hypotenuses to be congruent. $\begin{array}{r}\overline{AC}\cong \overline{MN}\end{array}$ .
  ::对HL来说,你需要的次元是相同的。

  播放段落

  Example 4
  ::例4

  播放段落

  Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
  ::确定三角形是否一致。 如果是, 请写入一致语句, 以及您使用的一致假设或定理 。

  

  播放段落

  We know the two triangles are right triangles. The have one pair of legs that is congruent and their hypotenuses are congruent. This means that $\begin{array}{r}\mathrm{△}ABC\cong \mathrm{△}RQP\end{array}$ by HL.
  ::我们知道这两个三角形是右三角形。 双腿是一对相近的, 下角是一对。 这意味着 HL 的 ABC QP 。

  播放段落

  Example 5
  ::例5

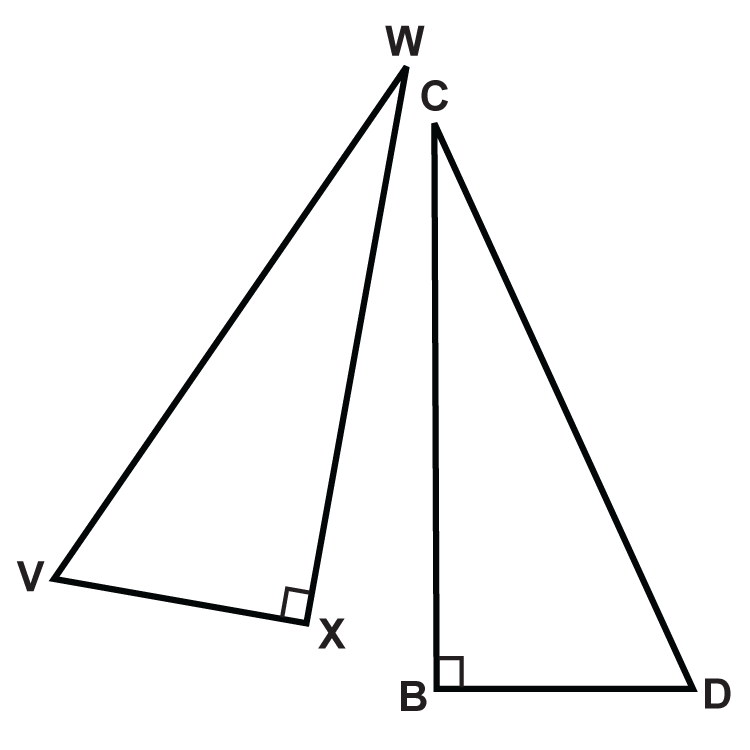
  播放段落

  Determine the additional piece of information needed to show the two triangles are congruent by HL.
  ::确定显示两个三角形所需的额外信息, 由 HL 匹配 。

  

  播放段落

  We already know one pair of legs is congruent and that they are right triangles. The additional piece of information we need is that the two hypotenuses are congruent, $\begin{array}{r}\overline{UT}\cong \overline{FG}\end{array}$ .
  ::我们已经知道一双双腿是相近的,它们也是正确的三角形。我们所需要的额外信息是,这两个下限是相近的,UT {FG}。

  播放段落

  Review
  ::回顾

  播放段落

  Using the HL Theorem, what additional information do you need to prove the two triangles are congruent?
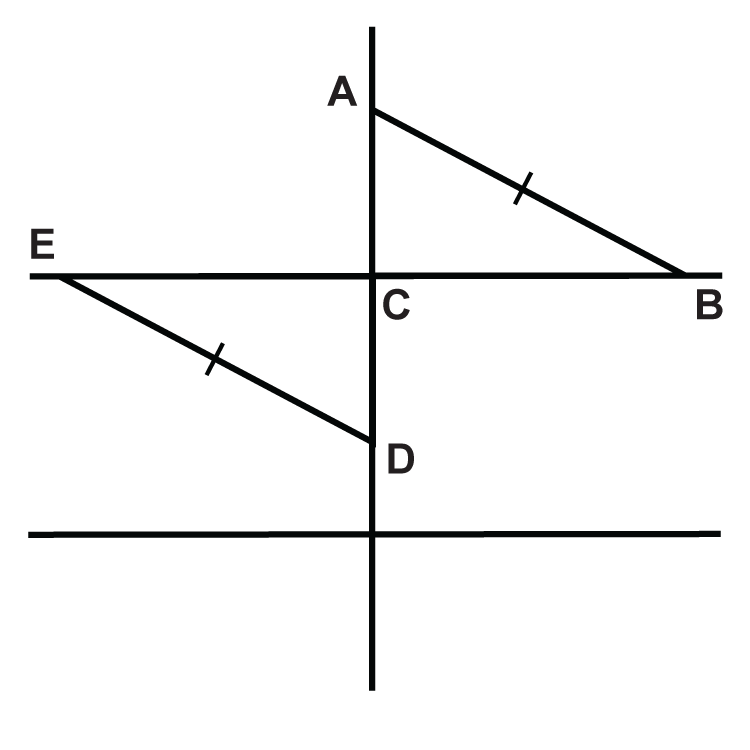
  ::使用 HL 定理, 您需要哪些额外信息来证明这两个三角形是相容的 ?

  1. 
  2. 
  3. 

  播放段落

  4. The triangles are formed by two parallel lines cut by a perpendicular transversal.  $\begin{array}{r}C\end{array}$ is the midpoint of $\begin{array}{r}\overline{AD}\end{array}$ . Complete the proof to show the two triangles are congruent. Questions 4-7 are within the proof.
  ::4. 三角形由两条平行线组成,两条平行线由直角横截面截断。C是AD的中点。完成证明两个三角形一致的证据。问题4-7在证据之内。

  

  Statement	Reason
  1. $\begin{array}{r}\mathrm{\angle }ACB\end{array}$ and $\begin{array}{r}\mathrm{\angle }DCE\end{array}$ are right angles.
  2.	Definition of a midpoint
  3.	Given
  4. $\begin{array}{r}\mathrm{\Delta }ACD\cong \mathrm{\Delta }DCE\end{array}$

  播放段落

  Based on the following details, are the two right triangles definitively congruent? The statements do not build off of each other.
  ::基于以下细节, 两个右三角是否完全一致? 声明不互相补充 。

  播放段落
  5. The hypotenuses of two right triangles are congruent.
     ::两个右三角形的下限是相近的。
  播放段落
  6. Both sets of legs in the two right triangles are congruent.
     ::两组右三角形的双腿是相同的。
  播放段落
  7. One set of legs are congruent in the two right triangles.
     ::两条右三角形的一双腿是相同的。
  播放段落
  8. The hypotenuses and one pair of legs are congruent in the two right triangles.
     ::两个右三角形的下肢和一双腿是相同的。
  播放段落
  9. One of the non right angles of the two right triangles is congruent.
     ::两个右三角形的一个非右角度是相同的。
  播放段落
  10. All of the angles of the two right triangles are congruent.
      ::两个右三角形的所有角度都是相同的。
  播放段落
  11. All of the sides of the two right triangles are congruent.
      ::两个右三角形的两侧都是相同的。
  播放段落
  12. Both triangles have one leg that is twice the length of the other.
      ::两个三角形的一条腿长于另一条腿的两倍。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

  播放段落

  Resources
  ::资源