6.6 草类
章节大纲
-
Trapezoids
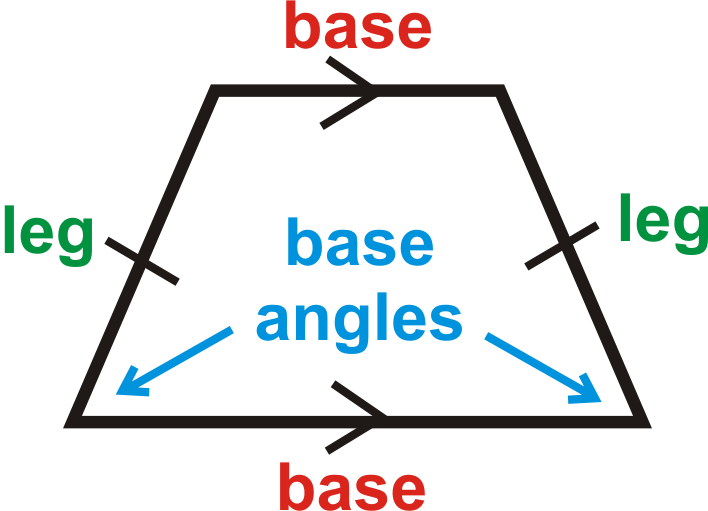
::细胞类A trapezoid is a quadrilateral with exactly one pair of parallel sides.
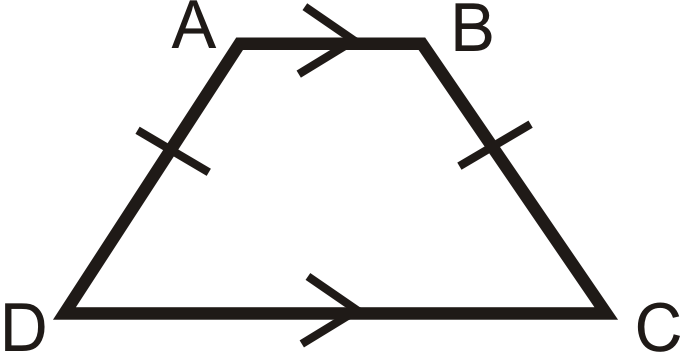
::甲状腺类是一种四边形, 有着一对齐的平行面。An isosceles trapezoid is a trapezoid where the non-parallel sides are congruent .
::等离子体类是非平行面相似的类类。The base angles of an isosceles trapezoid are congruent. If is an isosceles trapezoid, then and .
::asosceles capezoid 的底角是相似的。 如果 ABCD 是 asosceles capezoid, 则 {AB 和 {CD } 。The converse is also true. If a trapezoid has congruent base angles, then it is an isosceles trapezoid. The diagonals of an isosceles trapezoid are also congruent. The midsegment (of a trapezoid) is a line segment that connects the midpoints of the non-parallel sides:
::反之, 反之亦然 。 如果一个陷阱类具有相容的底角, 那么它就是一个等骨类底角 。 等骨类底座的对角也是相似的 。 中间部分( 类) 是连接非平行边中点的线条段 :There is only one midsegment in a trapezoid. It will be parallel to the bases because it is located halfway between them.
::捕鲸类中只有一个中间部分。 它会与基地平行, 因为它位于它们中间的半个位置 。Midsegment Theorem : The length of the midsegment of a trapezoid is the average of the lengths of the bases.
::密段定理 : 网格类的中间部分长度是基底长度的平均值 。If is the midsegment, then .
::如果EF是中间部分,那么EF=AB+CD2。What if you were told that the polygon is an isosceles trapezoid and that one of its base angles measures ? What can you conclude about its other base angle ?
::如果有人告诉您多边形ABCDIS 等离子体细胞类和其基角之一测量38+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++Examples
::实例For Examples 1 and 2, use the following information:
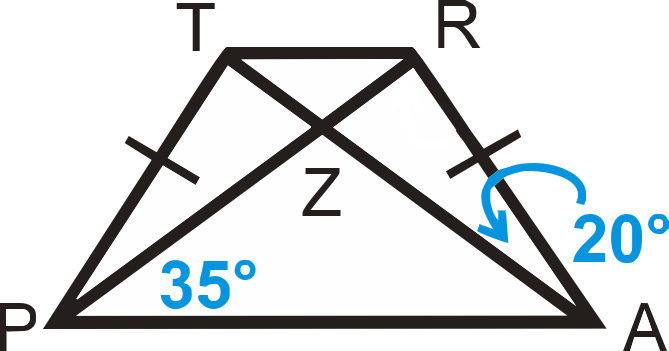
::关于例1和例2,请使用以下信息:is an isosceles trapezoid.
::TRAP是一个等骨细胞类。Example 1
::例1Find .
::找到MTPA。so .
::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~Example 2
::例2Find .
::去找玛拉Since , because they form a linear pair . By the Triangle Sum Theorem, .
::自 mPZA=110, mRZA=70 因为它们形成直线对。 依三角形sumTheorem, mRA=90。Example 3
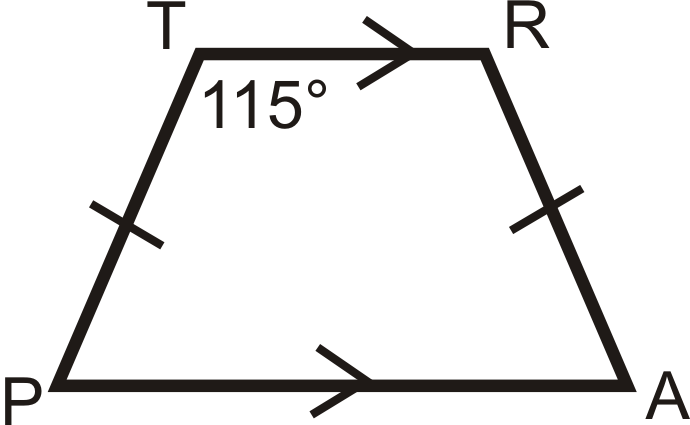
::例3Look at trapezoid below. What is ?
::看看下面的陷阱图 是什么?is an isosceles trapezoid. also.
::TRAP 是一个等离子细胞类。 mR=115。To find , set up an equation.
::为了找到maA, 设置一个方程。
::$115mA+mP=3602302A=360mA=mP2A=130mA=65Notice that . These angles will always be supplementary because of the Consecutive Interior Angles Theorem.
::注意 mR+mA=11565 180。 这些角度将永远是补充的, 因为有连续的内脏角度定理 。Example 4
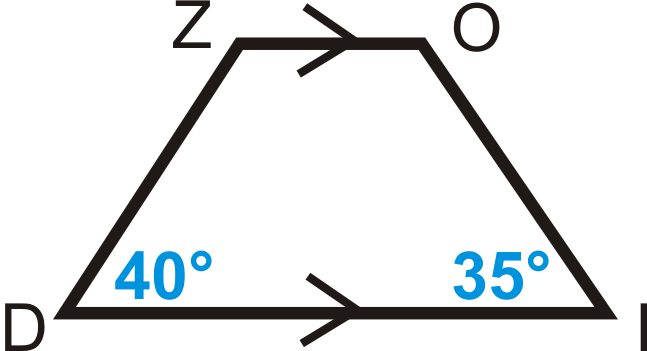
::例4Is an isosceles trapezoid? How do you know?
::ZOID是不是一个异骨骼类动物?你怎么知道的?, is not an isosceles trapezoid.
::4035, ZOID 不是一个等离子体。Example 5
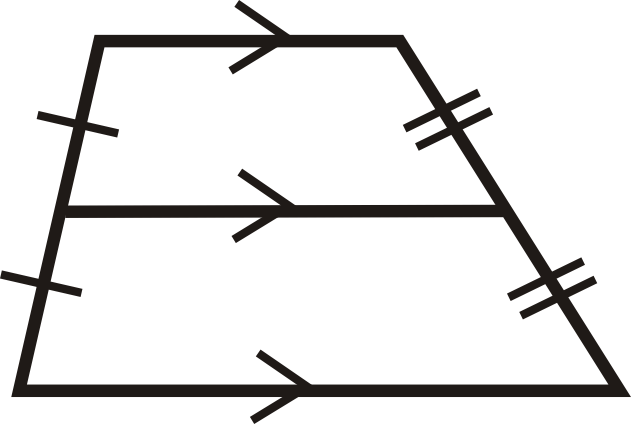
::例5Find . All figures are trapezoids with the midsegment marked as indicated.
::查找 x. 所有数字都是插件,中间部分标记如上所示。is the average of 12 and 26.
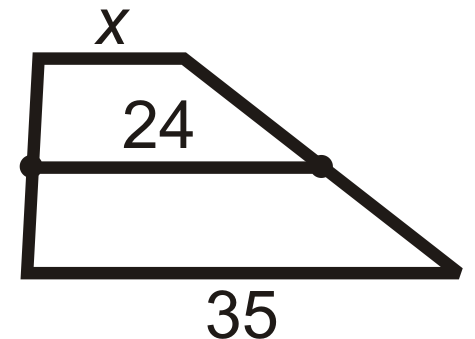
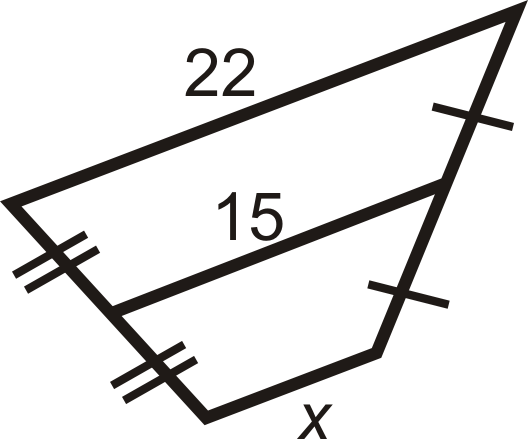
::x是12和26.12+262=382=19的平均值24 is the average of and 35.
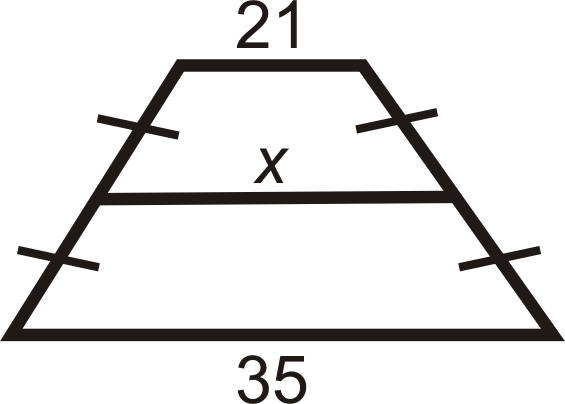
::24是x和35的平均数。
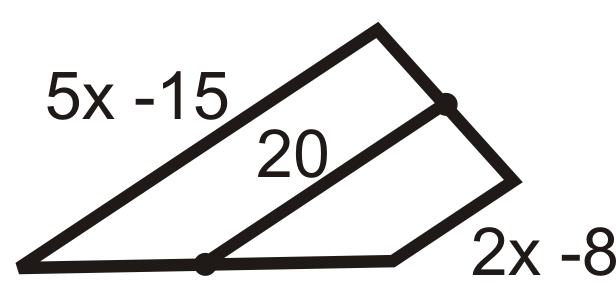
::x+352=24x+35=48x=1320 is the average of and .
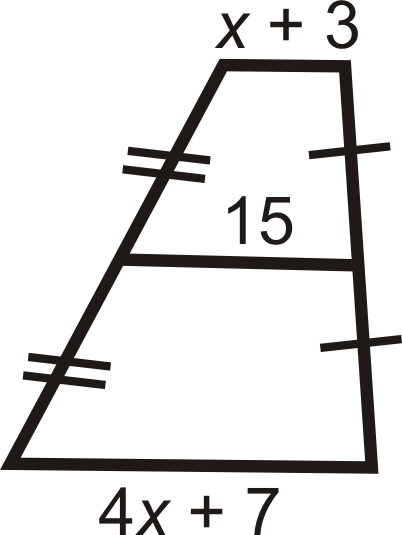
::20是5x-15和2x-8的平均值。
::5-15+2x-82=207x-23=407x=63x=9Review
::回顾1. Can the parallel sides of a trapezoid be congruent? Why or why not?
::1. 围网类的平行面能否一致?为什么或为什么不能?For questions 2-8, find the length of the midsegment or missing side.
::对于问题2-8,请找到中间部分的长度或缺失的侧面。Find the value of the missing variable(s).
::查找缺失变量的值。Find the lengths of the diagonals of the trapezoids below to determine if it is isosceles.
::查找下面的捕捉类星体的对角长度,以确定它是否为等分形。-
::A(3,3,2),B(1,3,3),C(3,-1),D(-4,4)-2 -
::A(-3,3),B(2,-2),C(-6,-6),D(-7,1)
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -