Course: 1.25 毕达哥里地名

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 毕达哥里地名

Collapse Expand
毕达哥里地名
What if you were working on a problem using the unit circle and had the value of one trig function (such as sine), but wanted instead to find the value of another trig function (such as cosine)? Is this possible?
::如果您正在使用单位圆处理一个问题,并且有一个三重函数(如正弦)的价值,而想要找到另一个三重函数(如余弦)的价值呢?这是可能的吗?

Try it with $\begin{aligned} \sin θ = \frac{1}{2} \end{aligned}$ .
::试试用"sin"12。

Pythagorean Identities
::毕达哥里地名

One set of identities are called the Pythagorean Identities because they rely on the . In other Concepts we used the Pythagorean Theorem to find the sides of right triangles.
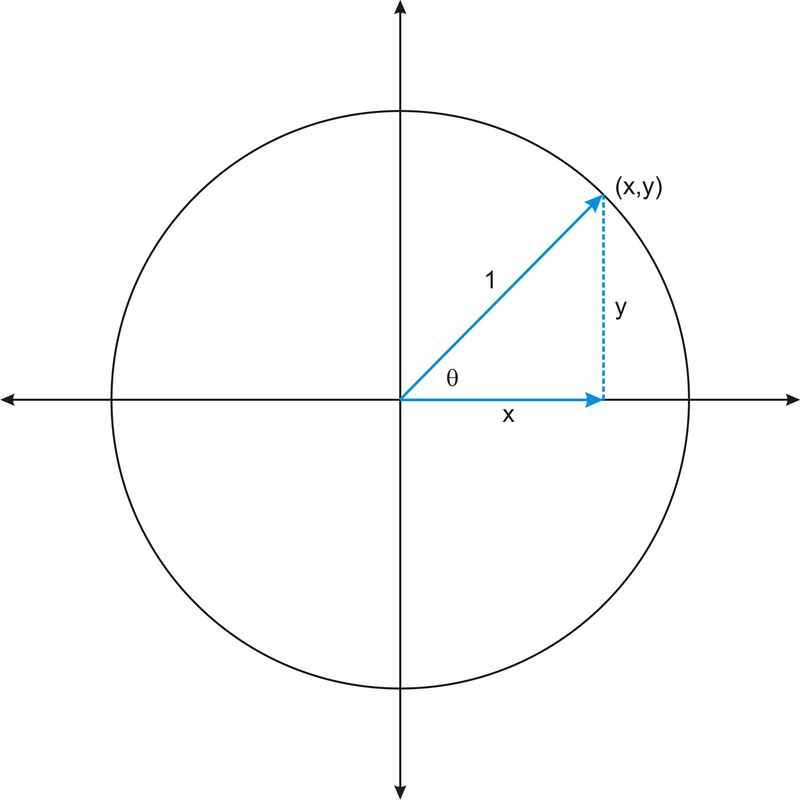
::一种身份被称为毕达哥里族身份,因为他们依赖这些身份。在其他概念中,我们使用毕达哥里族神话来寻找右三角形的侧面。

Consider the way that the trig functions are defined. Let’s look at the unit circle:
::考虑如何定义三角函数。让我们看看单位圆 :

The legs of the right triangle are $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . The hypotenuse is 1. Therefore the following equation is true for all $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ on the unit circle:
::右三角的腿为 x 和 y。下限为 1 。因此,以下方程对单位圆上的所有 x 和 y 来说是真实的 :

$\begin{aligned} x^{2} + y^{2} = 1 \end{aligned}$

::x2+y2=1

Now remember that on the unit circle, $\begin{aligned} \cos θ = x \end{aligned}$ and $\begin{aligned} \sin θ = y \end{aligned}$ . Therefore the following equation is an identity :
::现在记住单位圆、 cosx 和 siny 。因此, 以下方程式是一个身份 :

$\begin{aligned} \cos^{2} θ + \sin^{2} θ = 1 \end{aligned}$

::CO2=%sin2=%1

Note: Writing the exponent 2 after the $\begin{aligned} c o s \end{aligned}$ and $\begin{aligned} s i n \end{aligned}$ is the standard way of writing exponents. Just keeping mind that $\begin{aligned} \cos^{2} θ \end{aligned}$ means $\begin{aligned} (\cos θ)^{2} \end{aligned}$ and $\begin{aligned} \sin^{2} θ \end{aligned}$ means $\begin{aligned} (\sin θ)^{2} \end{aligned}$ .
::注:在罪与罪之后写出前言2是写出前言的标准方式。只需记住, cos2 意谓 (cos) 2 和 sin2 意谓 (sin) 2 。

We can use this identity to find the value of the sine function, given the value of the cosine, and vice versa. We can also use it to find other identities.
::我们可以使用此身份来找到正弦函数的价值, 以给定余弦值, 反之亦然。我们也可以使用它来寻找其它身份。

Using Pythagorean Identities
::使用毕达哥里身份

1. What is the value of $\begin{aligned} \sin θ \end{aligned}$ ?
::1. 罪恶的价值是什么?

If $\begin{aligned} \cos θ = \frac{1}{4} \end{aligned}$ what is the value of $\begin{aligned} \sin θ \end{aligned}$ ? Assume that $\begin{aligned} θ \end{aligned}$ is an angle in the first quadrant.
::如果cos14 什么是罪的值?假设这是第一个象限的一个角度。

$\begin{aligned} \sin θ = \frac{\sqrt{15}}{4} \end{aligned}$
::问题154

$\begin{aligned} \cos^{2} θ + \sin^{2} θ & = 1 \\ {(\frac{1}{4})}^{2} + \sin^{2} θ & = 1 \\ \frac{1}{16} + \sin^{2} θ & = 1 \\ \sin^{2} θ & = 1 - \frac{1}{16} \\ \sin^{2} θ & = \frac{15}{16} \\ \sin θ & = \pm \sqrt{\frac{15}{16}} \\ \sin θ & = \pm \frac{\sqrt{15}}{4} \end{aligned}$

::===================================================================================================================================

Remember that it was given that $\begin{aligned} θ \end{aligned}$ is an angle in the first quadrant. Therefore the sine value is positive, so $\begin{aligned} \sin θ = \frac{\sqrt{15}}{4} \end{aligned}$ .
::记住, 是第一个象限的一个角度。因此正弦值是正的, 所以sin_ 154 。

2. Use the identity $\begin{aligned} \cos^{2} θ + \sin^{2} θ = 1 \end{aligned}$ to show that $\begin{aligned} \cot^{2} θ + 1 = \csc^{2} θ \end{aligned}$
::2. 使用身份识别 Cos2sin21 来显示 cot21 = csc2

$\begin{aligned} \cos^{2} θ + \sin^{2} θ & = 1 & Divide both sides by \sin^{2} θ . \\ \frac{\cos^{2} θ + \sin^{2} θ}{\sin^{2} θ} & = \frac{1}{\sin^{2} θ} \\ \frac{\cos^{2} θ}{\sin^{2} θ} + \frac{\sin^{2} θ}{\sin^{2} θ} & = \frac{1}{\sin^{2} θ} & \frac{\sin^{2} θ}{\sin^{2} θ} = 1 \\ \frac{\cos^{2} θ}{\sin^{2} θ} + 1 & = \frac{1}{\sin^{2} θ} \\ \frac{\cos θ}{\sin θ} \times \frac{\cos θ}{\sin θ} + 1 & = \frac{1}{\sin θ} \times \frac{1}{\sin θ} & Write the squared functions in terms \\ of their factors. \\ \cot θ \times \cot θ + 1 & = \csc θ \times \csc θ & Use the quotient and reciprocal \\ identities. \\ \cot^{2} θ + 1 & = \csc^{2} θ & Write the functions as squared \\ functions. \end{aligned}$

::222211111222222222222222222222212222222222222222222222222221=11112222222222222222222222222222222222222222222222222 22222222 222222222222222222

3. What is the value of $\begin{aligned} \cos θ \end{aligned}$ ?
::3. Cos的价值是什么?

If $\begin{aligned} \sin θ = \frac{1}{2} \end{aligned}$ what is the value of $\begin{aligned} \cos θ \end{aligned}$ ? Assume that $\begin{aligned} θ \end{aligned}$ is an angle in the first quadrant.
::如果sin12 什么是Cos的价值?假设这是第一个象限的一个角度。

$\begin{aligned} \cos θ = \sqrt{\frac{3}{4}} \end{aligned}$
::COS34

$\begin{aligned} \sin^{2} θ + \cos^{2} θ & = 1 \\ {(\frac{1}{2})}^{2} + \cos^{2} θ & = 1 \\ \frac{1}{4} + \cos^{2} θ & = 1 \\ \cos^{2} θ & = 1 - \frac{1}{4} \\ \cos^{2} θ & = \frac{3}{4} \\ \cos θ & = \pm \sqrt{\frac{3}{4}} \end{aligned}$

::=====================================================================================================================================================

Remember that it was given that $\begin{aligned} θ \end{aligned}$ is an angle in the first quadrant. Therefore the cosine value is positive, so $\begin{aligned} \cos θ = \sqrt{\frac{3}{4}} \end{aligned}$ .
::请记住, 是第一个象限的一个角度。因此, 余弦值是正值, 所以是cos34 。

Examples
::实例

Example 1
::例1

Earlier, you were asked how you could find the value of one trig function if you knew the value of another trig function.
::早些时候,有人问您如何找到一个 trig 函数的值,如果您知道另一个 trig 函数的值。

Since we now know that:
::既然我们现在知道:

$\begin{aligned} \sin^{2} θ + \cos^{2} θ = 1 \end{aligned}$
::和/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或/或//////////////////////////////////////////////////////////////////////////////////////////////

we can use this to help us compute the cosine of the angle from the problem at the beginning of this Concept. It was given at the beginning of this Concept that:
::我们可以用这个来帮助我们计算这个概念开头的问题角度的余弦值。这个概念的开头是:

$\begin{aligned} \sin θ = \frac{1}{2} \end{aligned}$
::问题12

Therefore, $\begin{aligned} \sin^{2} θ = \frac{1}{4} \end{aligned}$
::因此, sin214

If we use this to solve for cosine:
::如果我们用这个解决余弦 :

$\begin{aligned} \sin^{2} θ + \cos^{2} θ = 1 \\ \cos^{2} θ = 1 - \sin^{2} θ \\ \cos^{2} θ = 1 - \frac{1}{4} \\ \cos^{2} θ = \frac{3}{4} \\ \cos θ = \frac{\sqrt{3}}{2} \end{aligned}$

::===========================================================================================================================================

Example 2
::例2

If $\begin{aligned} \cos θ = \frac{1}{2} \end{aligned}$ what is the value of $\begin{aligned} \sin θ \end{aligned}$ ? Assume that $\begin{aligned} θ \end{aligned}$ is an angle in the first quadrant.
::如果cos12 什么是罪的值?假设这是第一个象限的一个角度。

The solution is $\begin{aligned} \sin θ = \sqrt{\frac{3}{4}} \end{aligned}$ . We can see this from the Pythagorean Identity:
::我们从《毕达哥里人身份》中可以看到这一点:

$\begin{aligned} \cos^{2} θ + \sin^{2} θ & = 1 \\ {(\frac{1}{2})}^{2} + \sin^{2} θ & = 1 \\ \frac{1}{4} + \sin^{2} θ & = 1 \\ \sin^{2} θ & = 1 - \frac{1}{4} \\ \sin^{2} θ & = \frac{3}{4} \\ \sin θ & = \pm \sqrt{\frac{3}{4}} \end{aligned}$

::===========================================================================================================

Example 3
::例3

If $\begin{aligned} \sin θ = \frac{1}{8} \end{aligned}$ what is the value of $\begin{aligned} \cos θ \end{aligned}$ ? Assume that $\begin{aligned} θ \end{aligned}$ is an angle in the first quadrant.
::假设这是第一个象限的一个角度。

The solution is $\begin{aligned} \cos θ = \sqrt{\frac{63}{64}} \end{aligned}$ . We can see this from the Pythagorean Identity:
::答案是Cos6364。我们从《毕达哥里人身份》中可以看到这一点:

$\begin{aligned} \cos^{2} θ + \sin^{2} θ & = 1 \\ {(\frac{1}{8})}^{2} + \cos^{2} θ & = 1 \\ \frac{1}{64} + \cos^{2} θ & = 1 \\ \cos^{2} θ & = 1 - \frac{1}{64} \\ \cos^{2} θ & = \frac{63}{64} \\ \cos θ & = \pm \sqrt{\frac{63}{64}} \end{aligned}$

::COS2sin21(1818)2+cos21164+cos21cos21}1_164cos26364cos*6364

Example 4
::例4

If $\begin{aligned} \sin θ = \frac{1}{3} \end{aligned}$ what is the value of $\begin{aligned} \cos θ \end{aligned}$ ? Assume that $\begin{aligned} θ \end{aligned}$ is an angle in the first quadrant.
::假设这是第一个象限的一个角度。

The solution is $\begin{aligned} \cos θ = \sqrt{\frac{8}{9}} \end{aligned}$ . We can see this from the Pythagorean Identity:
::我们从《毕达哥里人身份》中可以看到这一点:

$\begin{aligned} \sin^{2} θ + \cos^{2} θ & = 1 \\ {(\frac{1}{3})}^{2} + \cos^{2} θ & = 1 \\ \frac{1}{9} + \cos^{2} θ & = 1 \\ \cos^{2} θ & = 1 - \frac{1}{9} \\ \cos^{2} θ & = \frac{8}{9} \\ \cos θ & = \pm \sqrt{\frac{8}{9}} \end{aligned}$

::2212(13)2+cos2119+cos2121cos21-19cos289cos_89

Re view
::回顾

If you know $\begin{aligned} \sin θ \end{aligned}$ , what other trigonometric value can you determine using a Pythagorean Identity?
::如果你知道什么是罪你还能用毕达哥里人的身份确定其他的三角值吗?

If you know $\begin{aligned} \sec θ \end{aligned}$ , what other trigonometric value can you determine using a Pythagorean Identity?
::如果您知道 sec , 您还能用 Pythagorian 身份来判断其他三角值吗 ?

If you know $\begin{aligned} \cot θ \end{aligned}$ , what other trigonometric value can you determine using a Pythagorean Identity?
::如果你知道Cot,你还能用 Pythagorian 身份来判断其他三角值吗?

If you know $\begin{aligned} \tan θ \end{aligned}$ , what other trigonometric value can you determine using a Pythagorean Identity?
::如果你了解Ttan,你还能用 Pythagorian 身份来判断其他的三角值吗?

For questions 5-14, assume all angles are in the first quadrant.
::对于问题5-14,假设所有角度都位于第一个象限。

If $\begin{aligned} \sin θ = \frac{1}{2} \end{aligned}$ , what is the value of $\begin{aligned} \cos θ \end{aligned}$ ?
::如果有错的话 12,Cosá的价值是什么?

If $\begin{aligned} \cos θ = \frac{\sqrt{2}}{2} \end{aligned}$ , what is the value of $\begin{aligned} \sin θ \end{aligned}$ ?
::如果cos22,什么是罪的价值?

If $\begin{aligned} \tan θ = 1 \end{aligned}$ , what is the value of $\begin{aligned} \sec θ \end{aligned}$ ?
::如果 tan #% 1, 秒值是多少 ?

If $\begin{aligned} \csc θ = \sqrt{2} \end{aligned}$ , what is the value of $\begin{aligned} \cot θ \end{aligned}$ ?
::如果csc2,那么Cot值是多少?

If $\begin{aligned} \sec θ = 2 \end{aligned}$ , what is the value of $\begin{aligned} \tan θ \end{aligned}$ ?
::如果第2项,那么TAN值是多少?

If $\begin{aligned} \cot θ = \sqrt{3} \end{aligned}$ , what is the value of $\begin{aligned} \csc θ \end{aligned}$ ?
::如果cot*% 3, Csc* 值是多少?

If $\begin{aligned} \cos θ = \frac{1}{4} \end{aligned}$ , what is the value of $\begin{aligned} \sin θ \end{aligned}$ ?
::如果cos14,什么是罪的价值?

If $\begin{aligned} \sec θ = 3 \end{aligned}$ , what is the value of $\begin{aligned} \tan θ \end{aligned}$ ?
::如果第3项,那么它的价值是多少?

If $\begin{aligned} \sin θ = \frac{1}{5} \end{aligned}$ , what is the value of $\begin{aligned} \cos θ \end{aligned}$ ?
::如果罪过15,Cosá的价值是什么?

If $\begin{aligned} \tan θ = \frac{\sqrt{3}}{3} \end{aligned}$ , what is the value of $\begin{aligned} \sec θ \end{aligned}$ ?
::如果塔尼33, 秒值是多少?

Use the identity $\begin{aligned} \sin^{2} θ + \cos^{2} θ = 1 \end{aligned}$ to show that $\begin{aligned} \tan^{2} θ + 1 = \sec^{2} θ \end{aligned}$
::使用身份 sin2cos21 来显示 tan21=sec2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

毕达哥里地名

Pythagorean Identities ::毕达哥里地名

Using Pythagorean Identities ::使用毕达哥里身份

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Re view ::回顾

Review (Answers) ::回顾(答复)

Pythagorean Identities
::毕达哥里地名

Using Pythagorean Identities
::使用毕达哥里身份

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Re view
::回顾

Review (Answers)
::回顾(答复)