课程： 2.1 雷达测量 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

半半径测量度

While working on an experiment in your school science lab, your teacher asks you to turn up a detector by rotating the knob $\begin{aligned} \frac{π}{2} \end{aligned}$ radians. You are immediately puzzled, since you don't know what a radian measure is or how far to turn the knob.
::在你的学校科学实验室做实验时,你的老师要求你通过旋转 knob 2 弧度来打开一个探测器。你马上被迷惑了,因为你不知道什么是光度测量值,或者要转弯到多远。

Measure of Radians
::雷达测量量

Until now, we have used degrees to measure angles. But, what exactly is a degree ? A degree is $\begin{aligned} \frac{1}{360^{t h}} \end{aligned}$ of a complete rotation around a circle. Radians are alternate units used to measure angles in trigonometry. Just as it sounds, a radian is based on the radius of a circle. One radian (abbreviated rad) is the angle created by bending the radius length around the arc of a circle. Because a radian is based on an actual part of the circle rather than an arbitrary division, it is a much more natural unit of angle measure for upper level mathematics.
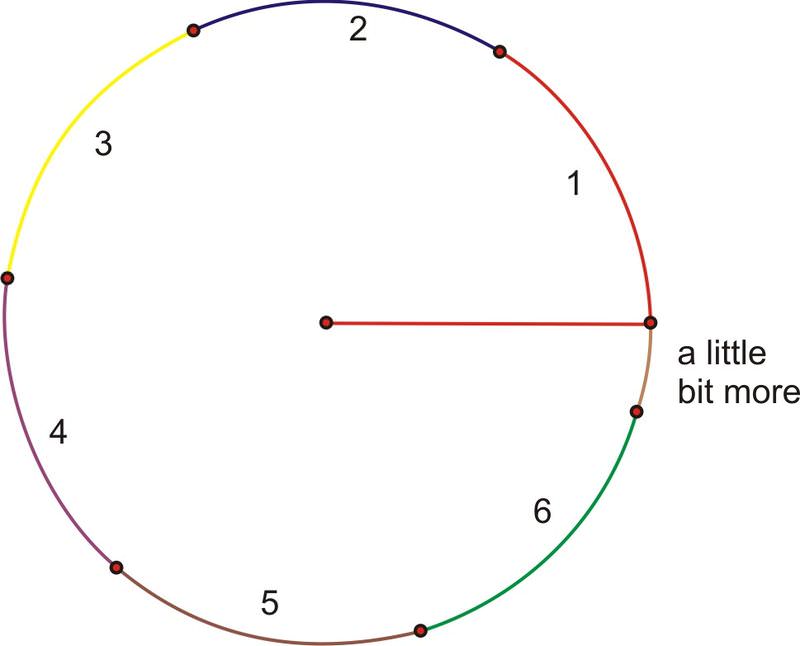
::到目前为止,我们已经使用度来测量角度。但是, 确切的度数是什么? 度数是圆周围完全旋转的第1360位。半径是用于测量三角测量角度的替代单位。正如它听起来一样, 弧度以圆的半径为基础。一个弧度( 缩放的弧度) 是弯曲圆圆弧周围半径长度所创造的角。因为弧度是基于圆的某个实际部分, 而不是任意的分隔, 它对于高层次数学来说, 是一个更自然的角度单位。

What if we were to rotate all the way around the circle? Continuing to add radius lengths, we find that it takes a little more than 6 of them to complete the rotation.
::如果我们绕圆圈绕圈旋转,会怎样?继续增加半径长度,我们发现完成旋转需要略多于6个。

Recall from geometry that the arc length of a complete rotation is the circumference, where the formula is equal to $\begin{aligned} 2 π \end{aligned}$ times the length of the radius. $\begin{aligned} 2 π \end{aligned}$ is approximately 6.28, so the circumference is a little more than 6 radius lengths. Or, in terms of radian measure, a complete rotation (360 degrees) is $\begin{aligned} 2 π \end{aligned}$ radians.
::从几何学上回顾,完全旋转的弧长度是环形,其公式等于半径长度的22倍。 2约为6.28, 环形小于6半径长度。或者,就弧度测量而言,完全旋转(360度)为2弧度。

\begin{aligned} 360 degrees = 2 π radians \end{aligned}

::360度=2弧度

With this as our starting point, we can find the radian measure of other angles. Half of a rotation, or 180 degrees, must therefore be $\begin{aligned} π \end{aligned}$ radians, and 90 degrees must be $\begin{aligned} \frac{1}{2} π \end{aligned}$ , written $\begin{aligned} \frac{π}{2} \end{aligned}$ .
::以此为起点, 我们可以找到其他角度的弧度量度。因此, 旋转的一半, 或180度, 必须是弧度, 90 度必须是 12 °, 写为 2 。

Extending the radian measure past the first quadrant, the quadrantal angles have been determined, except $\begin{aligned} 270^{\circ} \end{aligned}$ . Because $\begin{aligned} 270^{\circ} \end{aligned}$ is halfway between $\begin{aligned} 180^{\circ} \end{aligned}$ $\begin{aligned} (π) \end{aligned}$ and $\begin{aligned} 360^{\circ} \end{aligned}$ $\begin{aligned} (2 π) \end{aligned}$ , it must be $\begin{aligned} 1.5 π \end{aligned}$ , usually written $\begin{aligned} \frac{3 π}{2} \end{aligned}$ .
::在将弧度量扩展至第一个象限时,除270外,四方形角度已经确定。由于270介于180()和360()之间,所以必须是1.5,通常写为32。

For the $\begin{aligned} 45^{\circ} \end{aligned}$ angles, the radians are all multiples of $\begin{aligned} \frac{π}{4} \end{aligned}$ .
::45角的弧度是44的倍数。

For example, $\begin{aligned} 135^{\circ} \end{aligned}$ is $\begin{aligned} 3 \cdot 45^{\circ} \end{aligned}$ . Therefore, the radian measure should be $\begin{aligned} 3 \cdot \frac{π}{4} \end{aligned}$ , or $\begin{aligned} \frac{3 π}{4} \end{aligned}$ . Here are the rest of the multiples of $\begin{aligned} 45^{\circ} \end{aligned}$ , in radians:
::例如, 135是 345。因此, 弧度应该为 34, 或 34。下面是45的倍数中的其他数, 以弧度计 :

Notice that the additional angles in the drawing all have reference angles of 45 degrees and their radian measures are all multiples of $\begin{aligned} \frac{π}{4} \end{aligned}$ . All of the even multiples are the quadrantal angles and are reduced, just like any other fraction.
::请注意绘图中的额外角度都具有45度的参考角度,其弧度测量为 ++4 的倍数。所有偶数都是四角角,并被缩小,就像任何其他部分一样。

Let's do some problems that involve radian measures.
::让我们来做一些问题涉及到光度测量。

1. Find the radian measure of these angles.
::1. 找出这些角的弧度。

Angle in Degrees	Angle in Radians
90	$\begin{aligned} \frac{π}{2} \end{aligned}$
45
30

Because 45 is half of 90, half of $\begin{aligned} \frac{1}{2} π \end{aligned}$ is $\begin{aligned} \frac{1}{4} π \end{aligned}$ . 30 is one-third of a right angle, so multiplying gives:
::因为45是90的一半,12的一半是14。 30是正确角度的三分之一, 所以乘法提供:

\begin{aligned} \frac{π}{2} \times \frac{1}{3} = \frac{π}{6} \end{aligned}

and because 60 is twice as large as 30:
::因为60是30的两倍

\begin{aligned} 2 \times \frac{π}{6} = \frac{2 π}{6} = \frac{π}{3} \end{aligned}

Here is the completed table:
::以下是完整的表格:

Angle in Degrees	Angle in Radians
$\begin{aligned} 90 \end{aligned}$	$\begin{aligned} \frac{π}{2} \end{aligned}$
$\begin{aligned} 45 \end{aligned}$	$\begin{aligned} \frac{π}{4} \end{aligned}$
$\begin{aligned} 30 \end{aligned}$	$\begin{aligned} \frac{π}{6} \end{aligned}$

There is a formula to convert between radians and degrees that you may already have discovered while doing this example. However, many angles that are commonly used can be found easily from the values in this table. For example, most students find it easy to remember 30 and 60. 30 is $\begin{aligned} π \end{aligned}$ over 6 and 60 is $\begin{aligned} π \end{aligned}$ over 3 . Knowing these angles, you can find any of the special angles that have reference angles of 30 and 60 because they will all have the same denominators. The same is true of multiples of $\begin{aligned} \frac{π}{4} \end{aligned}$ (45 degrees) and $\begin{aligned} \frac{π}{2} \end{aligned}$ (90 degrees).
::使用此示例时您可能已经发现的弧度和度之间的转换公式。但是, 从本表格的值中可以很容易地找到许多常用角度。例如,大多数学生发现很容易记住 30 和 60 30, 6 和 60 是。了解这些角度, 您可以找到任何特殊角度, 其参考角度为 30 和 60 , 因为它们都有相同的分母。 4 4 ( 45 度) 和 % 2 ( 90 度) 的倍数也是如此。

2. Complete the following radian measures by counting in multiples of $\begin{aligned} \frac{π}{3} \end{aligned}$ and $\begin{aligned} \frac{π}{6} \end{aligned}$ :
::2. 以3和6的倍数计,完成以下弧度测量:

Notice that all of the angles with 60-degree reference angles are multiples of $\begin{aligned} \frac{π}{3} \end{aligned}$ , and all of those with 30-degree reference angles are multiples of $\begin{aligned} \frac{π}{6} \end{aligned}$ . Counting in these terms based on this pattern, rather than converting back to degrees, will help you better understand radians.
::请注意,所有具有60度参考角的角均为 +3 的倍数,所有具有30度参考角的角均为 + 6 的倍数。以这些术语根据此模式计数,而不是转换回度,将有助于您更好地了解弧度。

3. Find the radian measure of these angles.
::3. 找出这些角的弧度。

Angle in Degrees	Angle in Radians
120	$\begin{aligned} \frac{2 π}{3} \end{aligned}$
180
240
270
300

Because 30 is one-third of a right angle, multiplying gives:
::因为30是正确角度的三分之一,乘法提供:

\begin{aligned} \frac{π}{2} \times \frac{1}{3} = \frac{π}{6} \end{aligned}

adding this to the known value for ninety degrees of $\begin{aligned} \frac{π}{2} \end{aligned}$ :
::将它添加到已知值的 90 °% 2 :

\begin{aligned} \frac{π}{2} + \frac{π}{6} = \frac{3 π}{6} + \frac{π}{6} = \frac{4 π}{6} = \frac{2 π}{3} \end{aligned}

Here is the completed table:
::以下是完整的表格:

Angle in Degrees	Angle in Radians
$\begin{aligned} 120 \end{aligned}$	$\begin{aligned} \frac{2 π}{3} \end{aligned}$
$\begin{aligned} 180 \end{aligned}$	$\begin{aligned} π \end{aligned}$
$\begin{aligned} 240 \end{aligned}$	$\begin{aligned} \frac{4 π}{3} \end{aligned}$
$\begin{aligned} 300 \end{aligned}$	$\begin{aligned} \frac{5 π}{3} \end{aligned}$

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about rotating the knob.

::早些时候,有人给了你一个旋转把手的问题。

Since $\begin{aligned} 45^{\circ} = \frac{π}{4} r a d \end{aligned}$ , then $\begin{aligned} 2 \times \frac{π}{4} = \frac{π}{2} = 2 \times 45^{\circ} \end{aligned}$ . Therefore, a turn of $\begin{aligned} \frac{π}{2} \end{aligned}$ is equal to $\begin{aligned} 90^{\circ} \end{aligned}$ , which is $\begin{aligned} \frac{1}{4} \end{aligned}$ of a complete rotation of the knob.
::从454rad, 然后242=2×45。因此, 2的转折等于 90, 即时钟完全旋转的14。

Example 2
::例2

Give the radian measure of $\begin{aligned} 60^{\circ} \end{aligned}$
::给以60的弧度量

30 is one-third of a right angle. This means that since $\begin{aligned} 90^{\circ} = \frac{π}{2} \end{aligned}$ , then $\begin{aligned} 30^{\circ} = \frac{π}{6} \end{aligned}$ . Therefore, multiplying gives:
::30 是右角的三分之一。这意味着, 从 90\\\2, 然后30\\6, 因此, 乘法给出 :

$\begin{aligned} \frac{π}{6} \times 2 = \frac{π}{3} \end{aligned}$

Example 3
::例3

Give the radian measure of $\begin{aligned} 75^{\circ} \end{aligned}$
::给定弧度为 75 的度量

15 is one-sixth of a right triangle. This means that since $\begin{aligned} 90^{\circ} = \frac{π}{2} \end{aligned}$ , then $\begin{aligned} 15^{\circ} = \frac{π}{12} \end{aligned}$ . Therefore, multiplying gives:
::15 是右三角形的六分之一。这意味着从 90\\\ 2 开始, 然后是 15\\ 12。因此, 乘法给出 :

$\begin{aligned} \frac{π}{12} \times 5 = \frac{5 π}{12} \end{aligned}$

Example 4
::例4

Give the radian measure of $\begin{aligned} 180^{\circ} \end{aligned}$
::给定180度的弧度

Since $\begin{aligned} 90^{\circ} = \frac{π}{2} \end{aligned}$ , then $\begin{aligned} 180^{\circ} = \frac{2 π}{2} = π \end{aligned}$
::从90岁开始,2岁,然后180岁,2岁,2岁,2岁

Review
::回顾

Find the radian measure of each angle.
::查找每个角度的弧度量。

$\begin{aligned} 90^{\circ} \end{aligned}$
$\begin{aligned} 120^{\circ} \end{aligned}$
$\begin{aligned} 300^{\circ} \end{aligned}$
$\begin{aligned} 330^{\circ} \end{aligned}$
$\begin{aligned} - 45^{\circ} \end{aligned}$
$\begin{aligned} 135^{\circ} \end{aligned}$

Find the degree measure of each angle.
::查找每个角度的度量。

$\begin{aligned} \frac{3 π}{2} \end{aligned}$
$\begin{aligned} \frac{5 π}{4} \end{aligned}$
$\begin{aligned} \frac{7 π}{6} \end{aligned}$
$\begin{aligned} \frac{π}{6} \end{aligned}$
$\begin{aligned} \frac{5 π}{3} \end{aligned}$
$\begin{aligned} π \end{aligned}$

Explain why if you are given an angle in degrees and you multiply it by $\begin{aligned} \frac{π}{180} \end{aligned}$ you will get the same angle in radians.
::解释为什么如果给您给定一个角度以度乘以 180 , 那么在弧度中会得到相同的角度。

Explain why if you are given an angle in radians and you multiply it by $\begin{aligned} \frac{180}{π} \end{aligned}$ you will get the same angle in degrees.
::解释一下,如果给您一个角度以弧度乘以180°乘以180°,您为何会得到相同的角度以度计。

Explain in your own words why it makes sense that there are $\begin{aligned} 2 π \end{aligned}$ radians in a circle.
::用你自己的话来解释为什么圆圈里有2弧度是有道理的。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

半半径测量度

Measure of Radians ::雷达测量量

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)