课程： 2.16 振幅、期间和频率

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节振幅、周期和频率

折叠展开
振幅、周期和频率
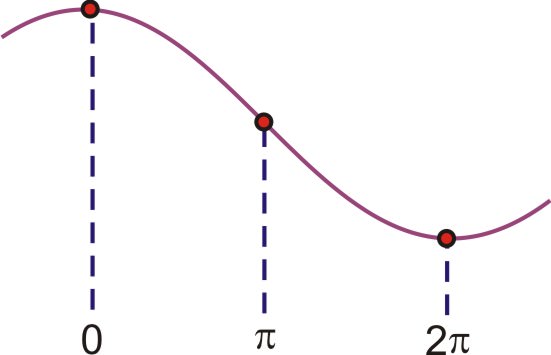
You are working in science lab one afternoon when your teacher asks you to do a little more advanced work with her on sound. Excited to help, you readily agree. She gives you a device that graphs sound waves as they come in through a microphone. She then gives you a "baseline" graph of what the sound wave's graph would look like:
::您在一个下午在科学实验室工作, 当您的老师要求您在声音上和她做一些更高级的工作。您非常乐意提供帮助, 您很容易同意。她给了您一个设备, 显示声波通过麦克风进入时的声波。然后她给了您一个“ 基线” 图 , 显示声音波的图像 :

She then asks you to plot the sound wave she's about to generate. However, she tells you that the sound wave will be twice as loud and twice as high in pitch as the baseline sound wave she gave you.
::她然后要求你绘制她即将产生的声波。然而,她告诉你,声波将比她给你的基线声波高一倍。

Can you determine how large the graph needs to be to plot the new sound wave? What about the spacing of numbers on the "x" axis?
::您能确定图形要绘制新声波需要多大的大小吗? “ x” 轴的数字间距如何 ?

Amplitude and Period
::振幅和周期

In other lessons you have dealt with how find the of a wave, or the period of a wave. Here we'll take a few minutes to work problems that involve both the amplitude and period, giving us two variables to work with when thinking about sinusoidal equations.
::在其他的教训中,您处理的是如何找到波的,或者波的周期。在这里,我们将花费几分钟的时间来解决既涉及振幅又涉及波的时期的问题, 给我们两个变量在思考正弦方程时可以工作。

Finding the Period, Amplitude, and Frequency
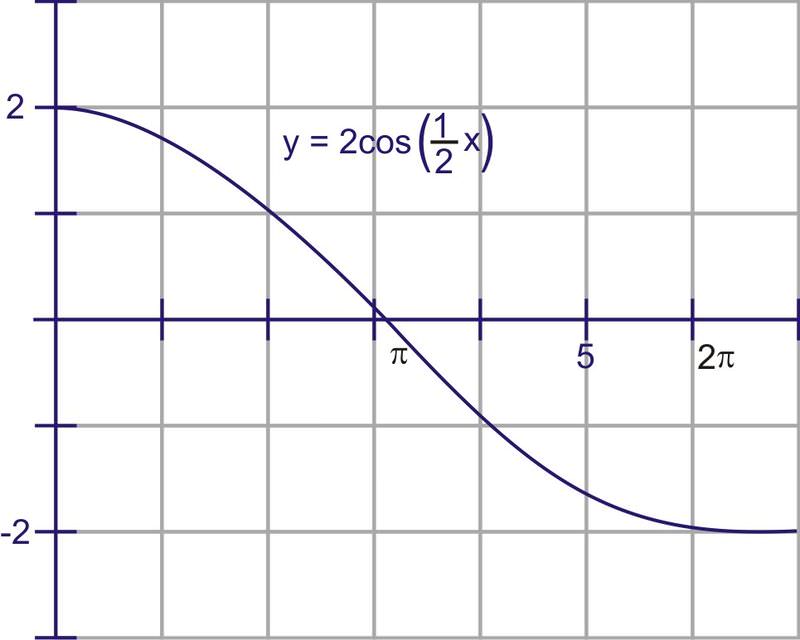
::时间、幅度和频率

1. Find the period, amplitude and frequency of $\begin{aligned} y = 2 \cos \frac{1}{2} x \end{aligned}$ and sketch a graph from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::1. 查找y=2cos=12x的周期、振幅和频率,并将图解绘制为0至2。

This is a cosine graph that has been stretched both vertically and horizontally. It will now reach up to 2 and down to -2. The frequency is $\begin{aligned} \frac{1}{2} \end{aligned}$ and to see a complete period we would need to graph the interval $\begin{aligned} [0, 4 π] \end{aligned}$ . Since we are only going out to $\begin{aligned} 2 π \end{aligned}$ , we will only see half of a wave. A complete cosine wave looks like this:
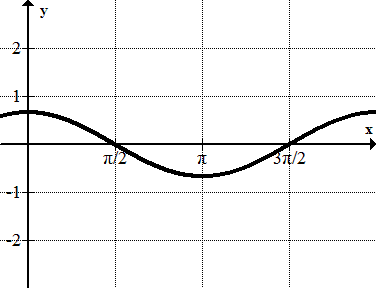
::这是一个垂直和水平拉伸的正弦图, 现在将达到2到2, 到-2。频率是 12, 要看到完整的时间段, 我们需要将间隔[ 0, 4] 绘制出来。由于我们只是向外延伸到 2, 我们只能看到半个波。完整的余弦波看起来是这样的 :

So, half of it is this:
::所以,其中一半是这个:

This means that this half needs to be stretched out so it finishes at $\begin{aligned} 2 π \end{aligned}$ , which means that at $\begin{aligned} π \end{aligned}$ the graph should cross the $\begin{aligned} x - \end{aligned}$ axis:
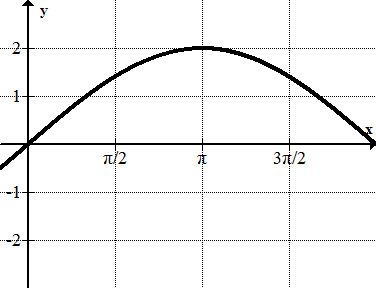
::这意味着这一半需要伸展, 以在 2 完成, 这意味着在时, 图形应该横过 x- 轴 :

The final sketch would look like this:
::最后的草图看起来是这样的:

$\begin{aligned} amplitude = 2, frequency = \frac{1}{2}, period = \frac{2 π}{\frac{1}{2}} = 4 π \end{aligned}$
::浮度= 2, 频率= 12, 周期= 212= 4

2. Identify the period, amplitude, frequency, and equation of the following sinusoid:
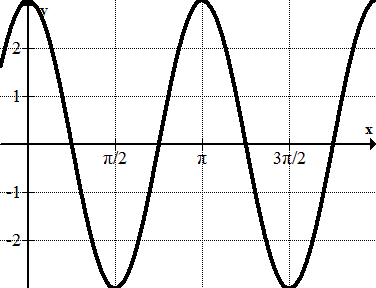
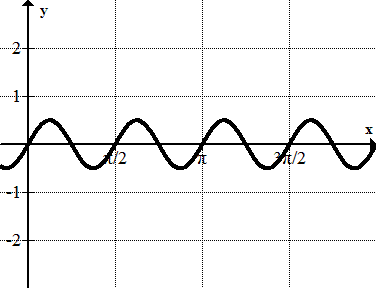
::2. 标明下列等离子体的周期、振幅、频率和方程:

The amplitude is 1.5. Notice that the units on the $\begin{aligned} x - \end{aligned}$ axis are not labeled in terms of $\begin{aligned} π \end{aligned}$ . This appears to be a sine wave because the $\begin{aligned} y - \end{aligned}$ intercept is 0.
::振幅为 1. 5。注意 x - 轴上的单位没有标记为 * 。这似乎是一个正弦波, 因为 y - intercept is 0 。

One wave appears to complete in 1 unit ( not $\begin{aligned} 1 π \end{aligned}$ units! ), so the period is 1. If one wave is completed in 1 unit, how many waves will be in $\begin{aligned} 2 π \end{aligned}$ units? In previous problems, you were given the frequency and asked to find the period using the following relationship:
::1 个波似乎以 1 个单位( 不是 1 个单位! ) 完成, 因此时间段是 1 。如果 1 个波以 1 个单位完成, 2 个单位将有多少个波? 在先前的问题中, 您得到了频率, 并被要求使用以下关系查找时间段 :

$\begin{aligned} p = \frac{2 π}{B} \end{aligned}$

::p=2B

Where $\begin{aligned} B \end{aligned}$ is the frequency and $\begin{aligned} p \end{aligned}$ is the period. With just a little bit of algebra, we can transform this formula and solve it for $\begin{aligned} B \end{aligned}$ :
::B 是频率, p 是周期。只要稍加代数, 我们可以转换这个公式, 解决 B :

$\begin{aligned} p = \frac{2 π}{B} \to B p = 2 π \to B = \frac{2 π}{p} \end{aligned}$

::p=2BBB=2B=2p

Therefore, the frequency is:
::因此,频率是:

$\begin{aligned} B = \frac{2 π}{1} = 2 π \end{aligned}$

::B=2%1=2______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

If we were to graph this out to $\begin{aligned} 2 π \end{aligned}$ we would see $\begin{aligned} 2 π \end{aligned}$ (or a little more than 6) complete waves.
::如果我们把这个图解为2,我们就会看到2(或略多于6)的完整波浪。

Replacing these values in the equation gives: $\begin{aligned} f (x) = 1.5 \sin 2 π x \end{aligned}$ .
::在方程中替换这些值时给出: f(x) =1.5sin2x。

3. Find the period, amplitude and frequency of $\begin{aligned} y = 3 \sin 2 x \end{aligned}$ and sketch a graph from 0 to $\begin{aligned} 6 π \end{aligned}$ .
::3. 查找y=3sin%2x的周期、振幅和频率,并将图解绘制为0至6。

This is a sine graph that has been stretched both vertically and horizontally. It will now reach up to 3 and down to -3. The frequency is 2 and so we will see the wave repeat twice over the interval from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::这是一个正弦图, 垂直和水平均被拉伸。现在将达到3, 下至 - 3。频率为 2 , 因此我们将看到波在 0 到 2 之间的间隔内重复两次。

$\begin{aligned} amplitude = 3, frequency = 2, period = \frac{2 π}{2} = π \end{aligned}$
::浮度=3,频率=2,周期=222

Examples
::实例

Example 1
::例1

Earlier, you were asked can you determine how large the graphs needs to be to plot the new sound wave.
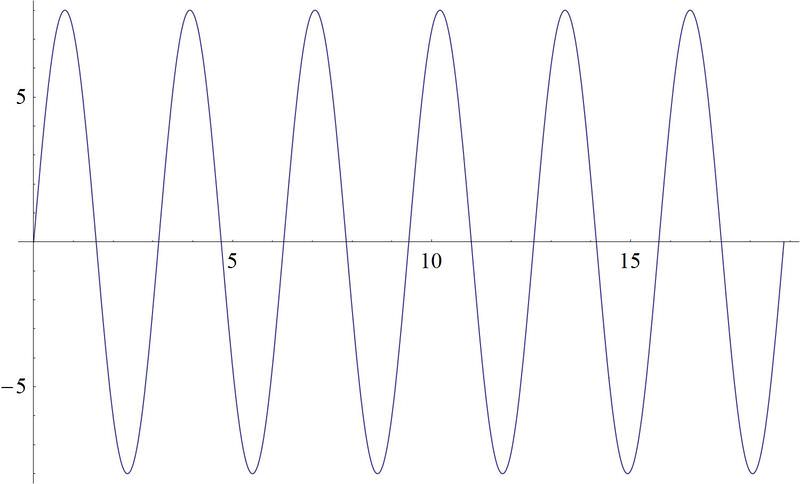
::早些时候,有人问过你,你能否确定图表需要多大的面积才能绘制出新的声波。

You know that the amplitude of the wave is the maximum height it makes above zero. You also know that the frequency is the number of cycles in a second. The scale of the graph you make should be able to take into account a maximum height of the wave that has been doubled, as well as a frequency that is twice as high. Your graph should look like this:
::您知道波的振幅是它使波高到零以上的最大高度。您也知道频率是周期数的第二个。您绘制的图形的尺度应该能够考虑到已经翻倍的波的最大高度, 以及两倍高的频率。您的图表应该这样看 :

Example 2
::例2

Identify the amplitude, period, and frequency of $\begin{aligned} y = \cos 2 x \end{aligned}$
::识别y=cos=%2x的振幅、期间和频率

period: $\begin{aligned} π \end{aligned}$ , amplitude: 1, frequency: 2
::周期: _______, 振幅: 1, 频率: 2

Example 3
::例3

Identify the amplitude, period, and frequency of $\begin{aligned} y = 3 \sin x \end{aligned}$
::识别y=3sinx的振幅、期间和频率

period: $\begin{aligned} 2 π \end{aligned}$ , amplitude: 3, frequency: 1
::周期: 2, 振幅: 3, 频率: 1

Example 4
::例4

Identify the amplitude, period, and frequency of $\begin{aligned} y = 2 \sin π x \end{aligned}$
::识别y=2sinx的振幅、期间和频率

period: 2, amplitude: 2, frequency: $\begin{aligned} π \end{aligned}$
::时段: 2, 振幅: 2, 频率:

Review
::回顾

Find the period, amplitude, and frequency of the following functions.
::查找下列函数的周期、振幅和频率。

$\begin{aligned} y = 2 \sin (3 x) \end{aligned}$
::y=2sin( 3x)

$\begin{aligned} y = 5 \cos (\frac{3}{4} x) \end{aligned}$
::y=5cos( 34x)

$\begin{aligned} y = 3 \cos (2 x) \end{aligned}$
::y=3cos( 2x)

$\begin{aligned} y = - 2 \sin (\frac{1}{2} x) \end{aligned}$
::y2sin( 12x)

$\begin{aligned} y = - \sin (2 x) \end{aligned}$
::ysin( 2x)

$\begin{aligned} y = \frac{1}{2} \cos (4 x) \end{aligned}$
::y=12cos( 4x)

Identify the equation of each of the following graphs. Assume there is no horizontal translation.
::显示下图的方程式。假设没有水平翻译。

Graph each of the following functions from 0 to $\begin{aligned} 2 π \end{aligned}$ .
::以下函数的图从 0 到 2 。

$\begin{aligned} y = 2 \cos (4 x) \end{aligned}$
::y=2cos( 4x)

$\begin{aligned} y = 3 \sin (\frac{5}{4} x) \end{aligned}$
::y=3sin( 54x)

$\begin{aligned} y = - \cos (2 x) \end{aligned}$
::ycos( 2x)

$\begin{aligned} y = - \sin (\frac{1}{2} x) \end{aligned}$
::ysin( 12x)

$\begin{aligned} y = 4 \sec (3 x) \end{aligned}$
::y=4sec( 3x)

$\begin{aligned} y = \frac{1}{2} \cos (3 x) \end{aligned}$
::y=12cos( 3x)

$\begin{aligned} y = 4 \tan (3 x) \end{aligned}$
::y=4tan( 3x)

$\begin{aligned} y = \frac{1}{2} \csc (3 x) \end{aligned}$
::y=12csc( 3x)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

振幅、周期和频率

Amplitude and Period ::振幅和周期

Finding the Period, Amplitude, and Frequency ::时间、幅度和频率

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Amplitude and Period
::振幅和周期

Finding the Period, Amplitude, and Frequency
::时间、幅度和频率

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)