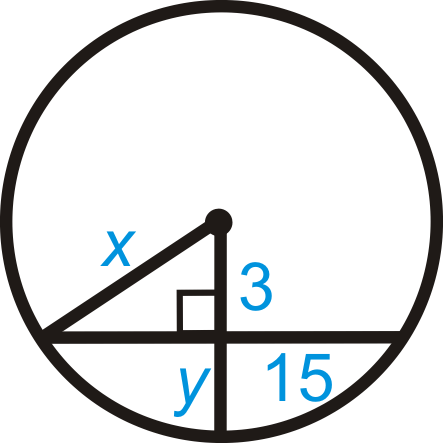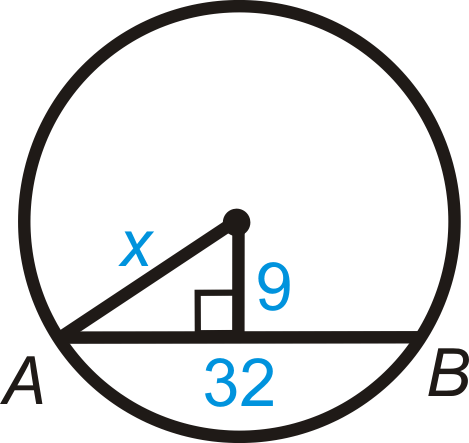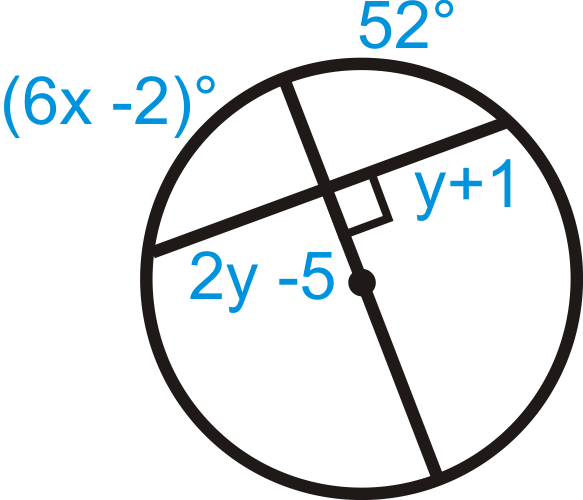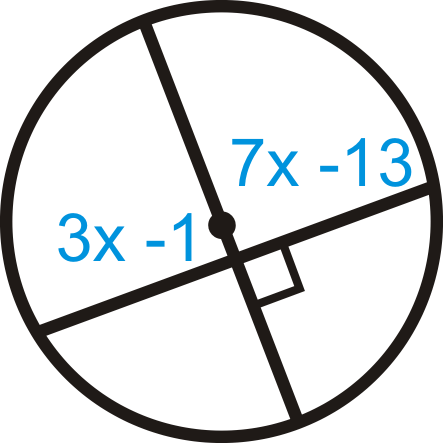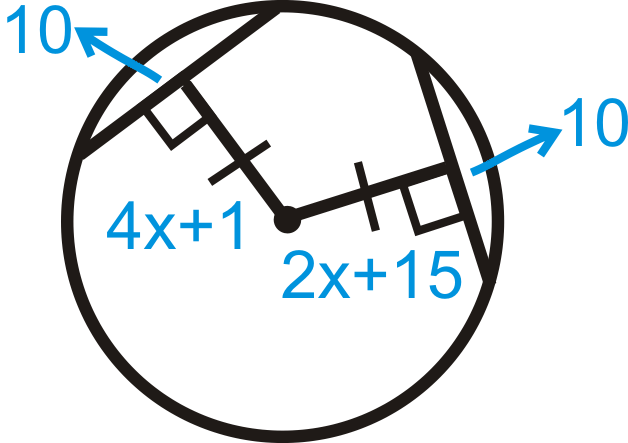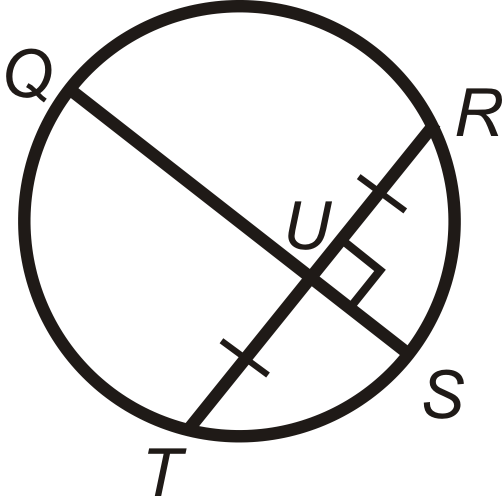Course: 9.4 圆形中的和弦

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 圆形中的和弦

Collapse Expand
圆形中的和弦
Chord Theorems
::和弦定理

There are several important theorems about chords that will help you to analyze circles better.
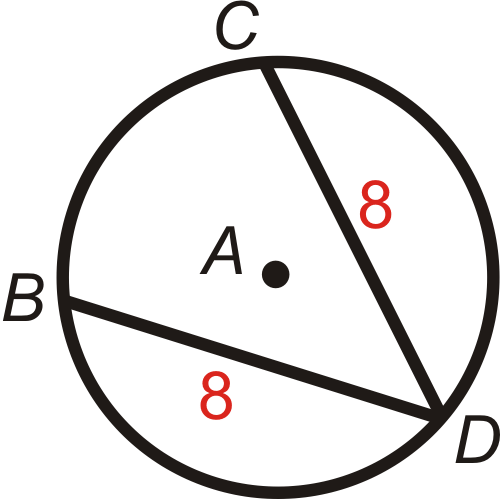
::有几个关于和弦的重要理论可以帮助你更好地分析圆圈。

1. Chord Theorem #1: In the same circle or congruent circles , minor arcs are congruent if and only if their corresponding chords are congruent.
::1. 和弦#1:在同一圆圈或正弦圆圈中,小弧在并且只有在相应的和弦一致的情况下才一致。

In both of these pictures, $\begin{aligned} \bar{B E} ≅ \bar{C D} \end{aligned}$ and $\begin{aligned} \hat{B E} ≅ \hat{C D} \end{aligned}$ .
::在这两张照片中,BECD和BECD。

2. Chord Theorem #2: The perpendicular bisector of a chord is also a diameter .
::2. 和弦理论#2:和弦的直径也是直径。

If $\begin{aligned} \bar{A D} ⊥ \bar{B C} \end{aligned}$ and $\begin{aligned} \bar{B D} ≅ \bar{D C} \end{aligned}$ then $\begin{aligned} \bar{E F} \end{aligned}$ is a diameter.
::如果ADBC和BDDC是直径

3. Chord Theorem #3: If a diameter is perpendicular to a chord, then the diameter bisects the chord and its corresponding arc .
::3. 和弦定理#3:如果直径与和弦垂直,则直径将和弦及其相应的弧分为两部分。

If $\begin{aligned} \bar{E F} ⊥ \bar{B C} \end{aligned}$ , then $\begin{aligned} \bar{B D} ≅ \bar{D C} \end{aligned}$ and $\begin{aligned} \hat{B E} ≅ \hat{E C} \end{aligned}$ .
::如果EF BC,那么BDD D和BEEC。

4. Chord Theorem #4: In the same circle or congruent circles, two chords are congruent if and only if they are equidistant from the center .
::4. 和弦4:在同一圆圈或相同圆圈中,如果而且只有在与中间的距离相等的情况下,两个和弦是相同的。

The shortest distance from any point to a line is the perpendicular line between them. If $\begin{aligned} F E = E G \end{aligned}$ and $\begin{aligned} \bar{E F} ⊥ \bar{E G} \end{aligned}$ , then $\begin{aligned} \bar{A B} \end{aligned}$ and $\begin{aligned} \bar{C D} \end{aligned}$ are equidistant to the center and $\begin{aligned} \bar{A B} ≅ \bar{C D} \end{aligned}$ .
::从任何一点到一条线的最短距离是它们之间的垂直线。如果FE=EG 和 EF = EG 和 EF = EG ,那么AB 和 CD 的距离就等于中间线和AB =CD 。

What if you were given a circle with two chords drawn through it? How could you determine if these two chords were congruent?
::假若你们获得一个圆形,有两根和弦通过它而绘制的圆形,你们怎么确定这两根和弦是否一致呢?

Examples
::实例

Example 1
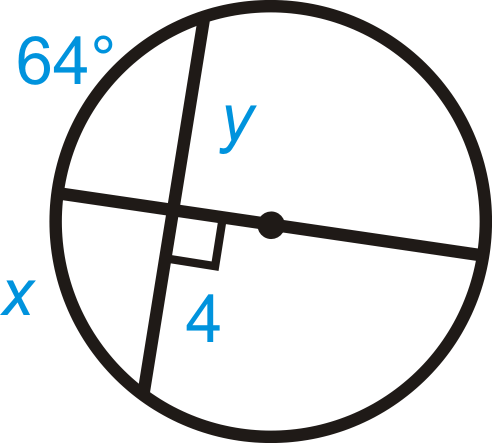
::例1

Find the value of $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::查找 x 和 y 的值。

The diameter is perpendicular to the chord, which means it bisects the chord and the arc. Set up equations for $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::直径直径与和弦垂直, 这意味着它将和弦和弧相切。为 x 和 y 设置方程式。

$\begin{aligned} (3 x - 4)^{\circ} & = (5 x - 18)^{\circ} y + 4 = 2 y + 1 \\ 14 & = 2 x 3 = y \\ 7 & = x \end{aligned}$

:3x-4)(5x-18)(y+4=2y+114=2x3=y7=x)

Example 2
::例2

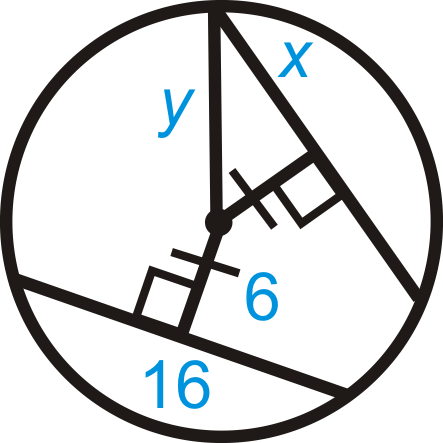
$\begin{aligned} B D = 12 \end{aligned}$ and $\begin{aligned} A C = 3 \end{aligned}$ in $\begin{aligned} ⨀ A \end{aligned}$ . Find the radius .
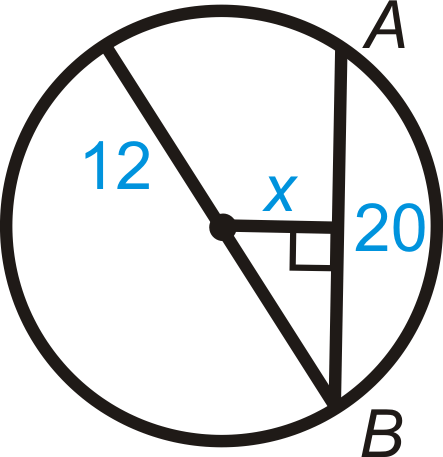
::BD=12 和 AC=3 在 A. 找到半径。

First find the radius. $\begin{aligned} \bar{A B} \end{aligned}$ is a radius, so we can use the right triangle $\begin{aligned} △ A B C \end{aligned}$ with hypotenuse $\begin{aligned} \bar{A B} \end{aligned}$ . From Chord Theorem #3, $\begin{aligned} B C = 6 \end{aligned}$ .
::首先找到半径。AB是一个半径, 所以我们可以使用右三角 ABC 和 AB 。来自Chord Theorem # 3, BC=6。

$\begin{aligned} 3^{2} + 6^{2} & = A B^{2} \\ 9 + 36 & = A B^{2} \\ A B & = \sqrt{45} = 3 \sqrt{5} \end{aligned}$

::32+62=AB29+36=AB2AB=45=35

Example 3
::例3

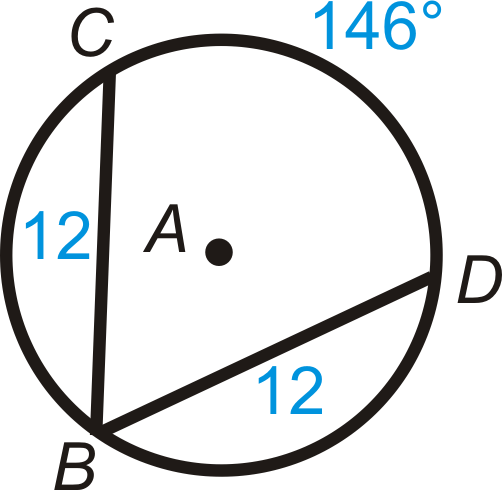
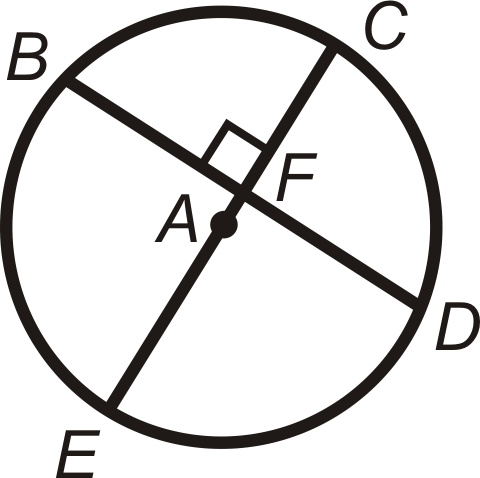
Use $\begin{aligned} ⨀ A \end{aligned}$ to answer the following.
::使用 {A 来回答以下问题。

If $\begin{aligned} m \hat{B D} = 125^{\circ} \end{aligned}$ , find $\begin{aligned} m \hat{C D} \end{aligned}$ .
::如果 mBD125, 找到 mCD。

$\begin{aligned} B D = C D \end{aligned}$ , which means the arcs are congruent too. $\begin{aligned} m \hat{C D} = 125^{\circ} \end{aligned}$ .
::BD=CD,这意味着弧也是一致的。 mCD=125\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\c\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\。\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

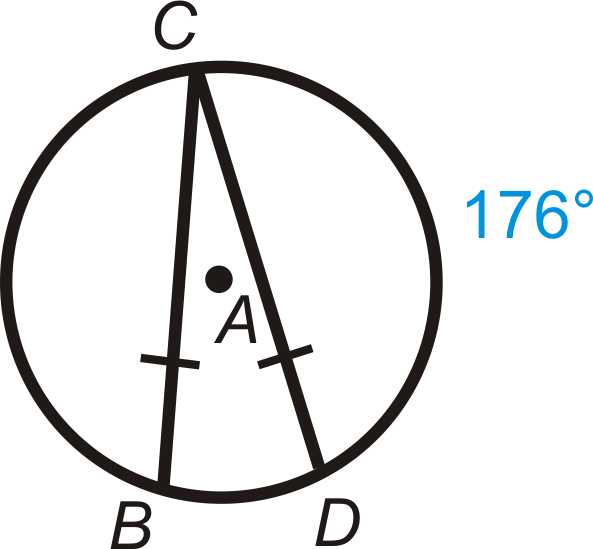
If $\begin{aligned} m \hat{B C} = 80^{\circ} \end{aligned}$ , find $\begin{aligned} m \hat{C D} \end{aligned}$ .
::如果 mBC80, 找到 mCD。

$\begin{aligned} m \hat{C D} ≅ m \hat{B D} \end{aligned}$ because $\begin{aligned} B D = C D \end{aligned}$ .
::mCD mBD 是因为BD=CD

$\begin{aligned} m \hat{B C} + m \hat{C D} + m \hat{B D} & = 360^{\circ} \\ 80^{\circ} + 2 m \hat{C D} & = 360^{\circ} \\ 2 m \hat{C D} & = 280^{\circ} \\ m \hat{C D} & = 140^{\circ} \end{aligned}$

::mBCmCDmBD360802mCD3602mCD280mCD140

Example 4
::例4

Find the values of $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::查找 x 和 y 的值。

The diameter is perpendicular to the chord. From Chord Theorem #3, $\begin{aligned} x = 6 \end{aligned}$ and $\begin{aligned} y = 75^{\circ} \end{aligned}$ .
::直径与和弦垂直。从弦理论 # 3, x=6 和y= 75 。

Example 5
::例5

Find the value of $\begin{aligned} x \end{aligned}$ .
::查找 x 的值。

Because the distance from the center to the chords is equal, the chords are congruent.
::因为从中间到和弦的距离是相等的, 和弦是相似的。

$\begin{aligned} 6 x - 7 & = 35 \\ 6 x & = 42 \\ x & = 7 \end{aligned}$

::6-7=356x=42x=7

Review
::回顾

Fill in the blanks.
::填满空白。

$\begin{aligned} \underline{} ≅ \bar{D F} \end{aligned}$
::# DF # # DF #

$\begin{aligned} \hat{A C} ≅ \underline{} \end{aligned}$
::AC

$\begin{aligned} \hat{D J} ≅ \underline{} \end{aligned}$
::DJ

$\begin{aligned} \underline{} ≅ \bar{E J} \end{aligned}$
::# Ej # # Ej #

$\begin{aligned} ∠ A G H ≅ \underline{} \end{aligned}$
::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

$\begin{aligned} ∠ D G F ≅ \underline{} \end{aligned}$
::DGF________________________________________________________________________________________________________________________________________________________________________________

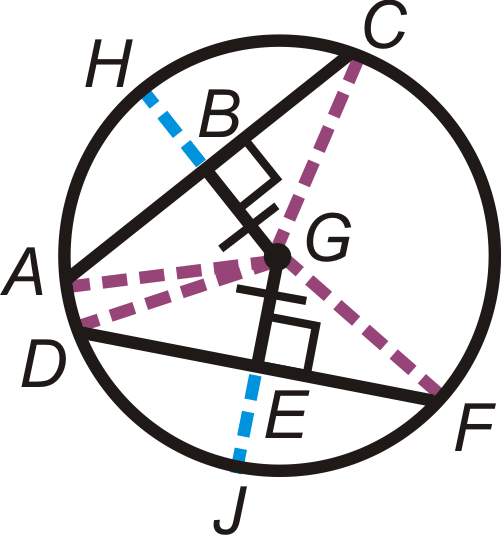
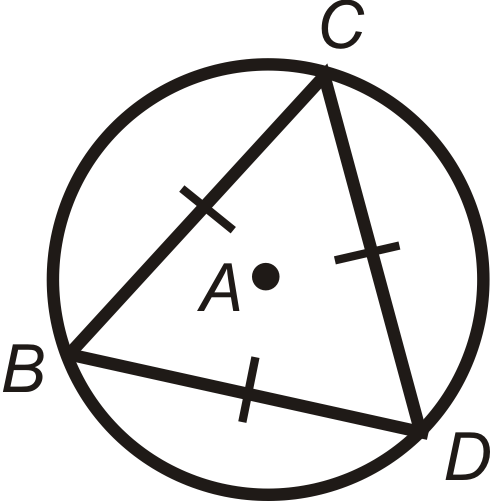
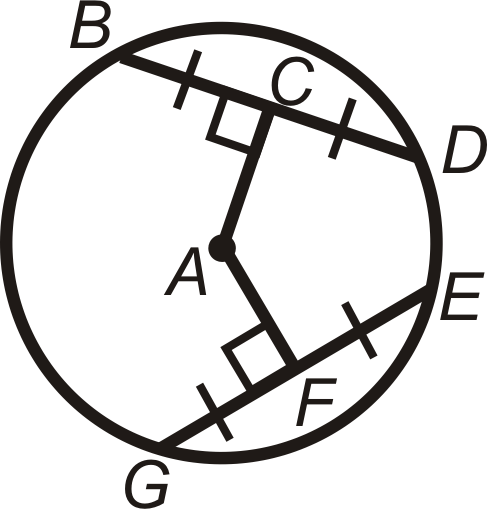
List all the congruent radii in $\begin{aligned} ⨀ G \end{aligned}$ .
::列出 G 中的所有一致的 radi 。

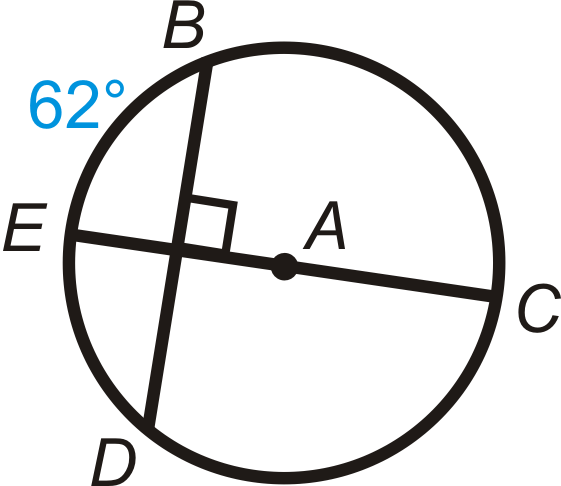
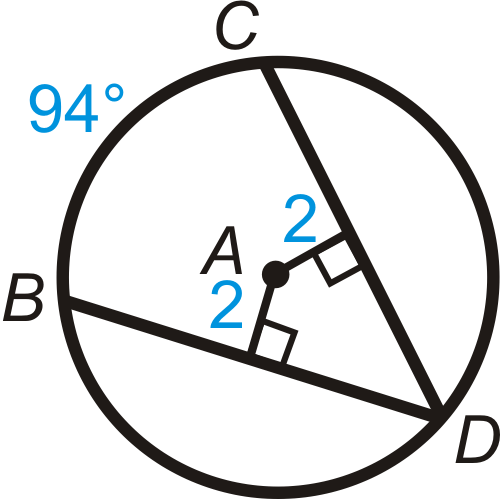
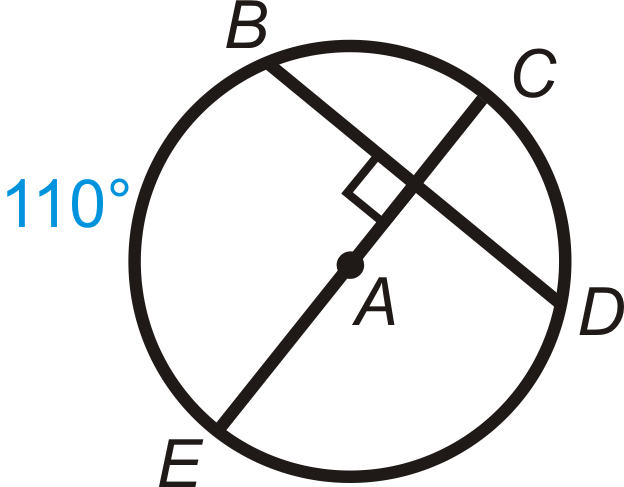
Find the value of the indicated arc in $\begin{aligned} ⨀ A \end{aligned}$ .
::查找 A 中显示的弧值。

$\begin{aligned} m \hat{B C} \end{aligned}$
::mBC

$\begin{aligned} m \hat{B D} \end{aligned}$
::mBD

$\begin{aligned} m \hat{B C} \end{aligned}$
::mBC

$\begin{aligned} m \hat{B D} \end{aligned}$
::mBD

$\begin{aligned} m \hat{B D} \end{aligned}$
::mBD

$\begin{aligned} m \hat{B D} \end{aligned}$
::mBD

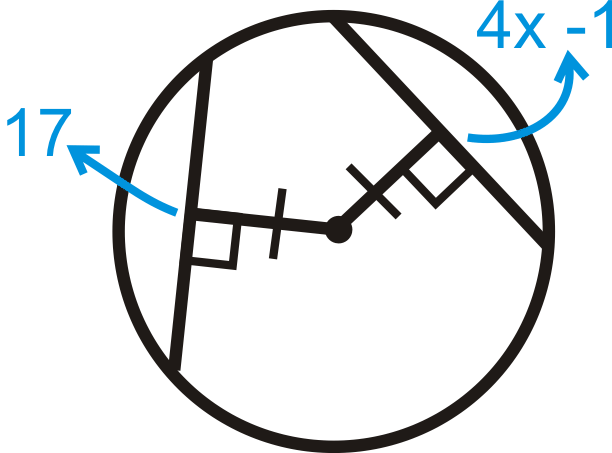
Find the value of $\begin{aligned} x \end{aligned}$ and/or $\begin{aligned} y \end{aligned}$ . Round your answer to the nearest tenth where needed.
::查找 x 和/ 或 Y 的值。需要时, 将您的答复按最接近的 10 键四舍五入。

$\begin{aligned} A B = 32 \end{aligned}$
::AB=32

$\begin{aligned} A B = 20 \end{aligned}$
::AB=20

Find $\begin{aligned} m \hat{A B} \end{aligned}$ in Question 17. Round your answer to the nearest tenth of a degree.
::在问题17中找到 mAB。将您的答复回合到最接近的 10 度。

Find $\begin{aligned} m \hat{A B} \end{aligned}$ in Question 22. Round your answer to the nearest tenth of a degree.
::在问题22中找到 mAB 。。。

In problems 25-27, what can you conclude about the picture? State a theorem that justifies your answer. You may assume that $\begin{aligned} A \end{aligned}$ is the center of the circle.
::在25-27号问题中,你能得出什么结论呢? 说明一个解释你答案的理论。你可以假设A是圆圈的中心。

Review (Answers)
::回顾(答复)

To see the answer key for this book, go to the and click on the Answer Key under the ' ' option.
::要查看本书的答案键, 请在“ ” 选项下点击答案键。

Section outline

General

圆形中的和弦

Chord Theorems ::和弦定理

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Chord Theorems
::和弦定理

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)