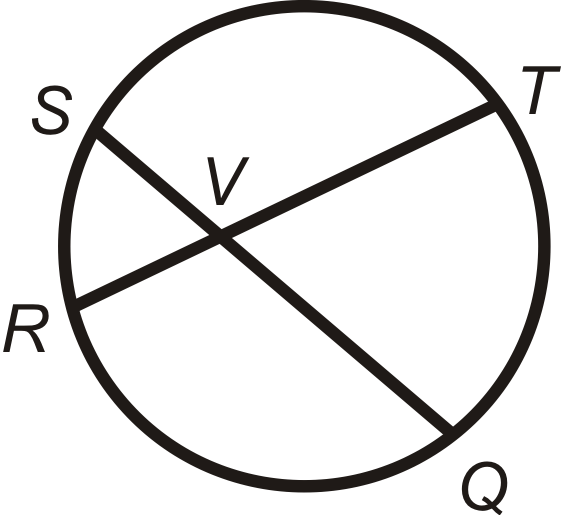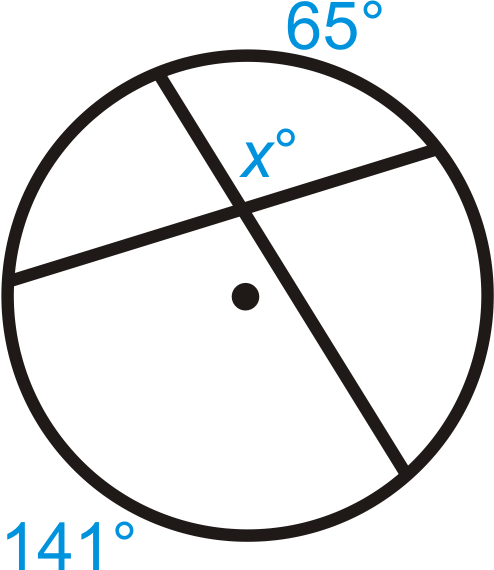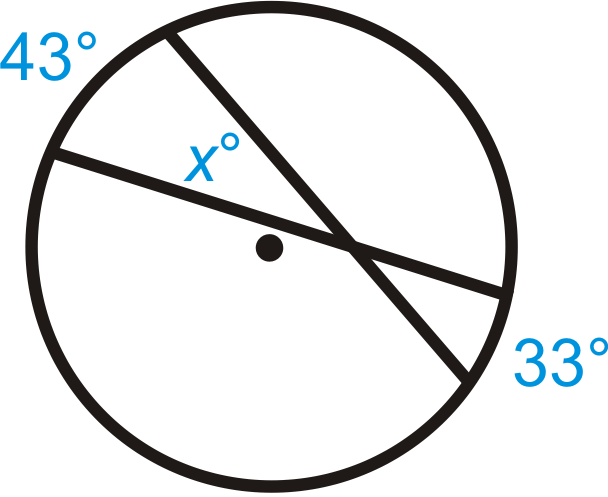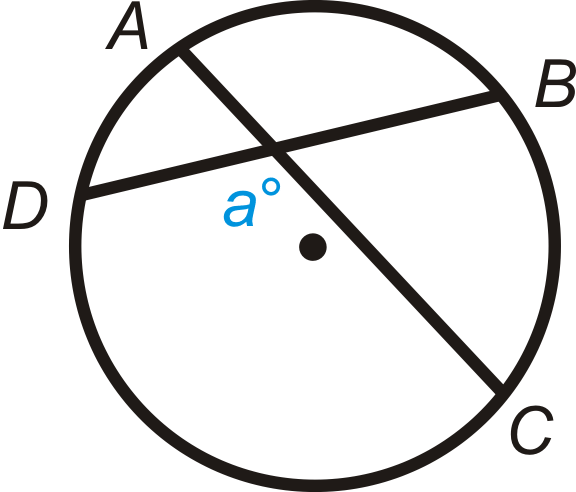课程： 9.7 圆圈内和圆圈内角

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

圆圈内外角角

Angles On and Inside a Circle
::圆圈内外角角

When we say an angle is on a circle , we mean the vertex is on the edge of the circle. One type of angle on a circle is the inscribed angle (see ). Another type of angle on a circle is one formed by a tangent and a chord .
::当我们说一个角度在圆上时,我们的意思是顶点在圆的边缘。圆上的一种角度是刻入的角度(见)。圆上另一种角度是正切和和和弦形成的一个角度。

Chord/Tangent Angle Theorem : The measure of an angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc .
::Chord/Tangent 角定理:由圆圆形交错的和弦形成角的度量是被截取弧的度量的一半。

$\begin{aligned} m ∠ D B A = \frac{1}{2} m \hat{A B} \end{aligned}$
::mDBA=12mAB

If two angles, with their vertices on the circle, intercept the same arc then the angles are congruent .
::如果两个角度,在圆圈上有它们的脊椎, 截取同样的弧, 那么角度是相同的。

An angle is inside a circle when the vertex lies anywhere inside the circle.
::当顶点位于圆内任何地方时,一个角度在圆内。

Intersecting Chords Angle Theorem: The measure of the angle formed by two chords that intersect inside a circle is the average of the measures of the intercepted arcs.
::交叉弦角理论:两个和弦在圆内交叉形成角的测量值是被截取弧的平均测量值。

\begin{aligned} m ∠ S V R & = \frac{1}{2} (m \hat{S R} + m \hat{T Q}) = \frac{m \hat{S R} + m \hat{T Q}}{2} = m ∠ T V Q \\ m ∠ S V T & = \frac{1}{2} (m \hat{S T} + m \hat{R Q}) = \frac{m \hat{S T} + m \hat{R Q}}{2} = m ∠ R V Q \end{aligned}

::mSVR=12( mSRmT2=mSRmT2=mTVQSVT=12(mSTmR)=mSTmR2=mRVQ

What if you were given a circle with either a chord and a tangent or two chords that meet at a common point ? How could you use the measure of the arc(s) formed by those circle parts to find the measure of the angles they make on or inside the circle?
::如果给您一个圆圈,有弦和正弦,或两个和弦,在一个共同点相交?如何用这些圆圈段所形成的弧的量度来测量圆圈上或圆圈内的角?

Examples
::实例

Example 1
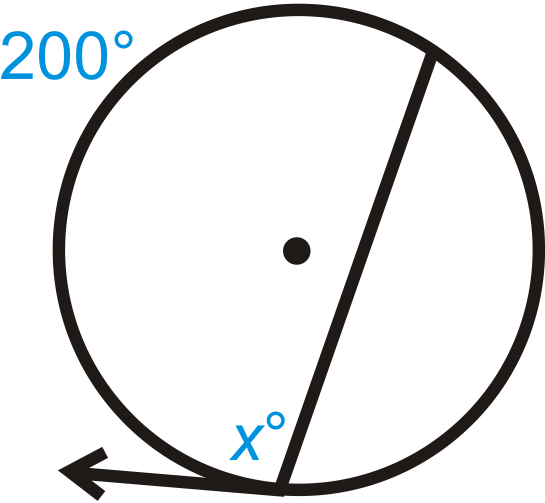
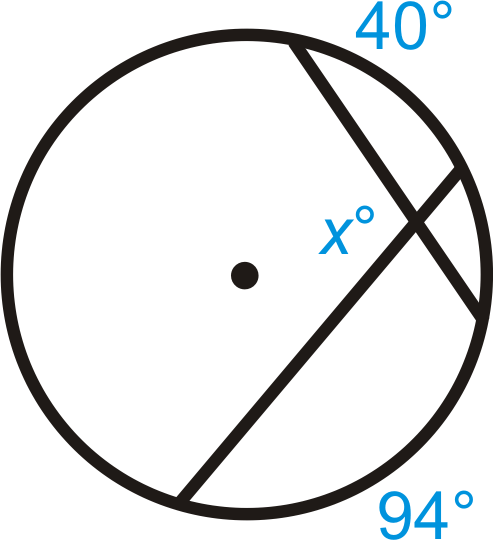
::例1

Find $\begin{aligned} x \end{aligned}$ .
::查找 x.

Use the Intersecting Chords Angle Theorem to write an equation.
::使用交叉弦角定理来写一个方程式。

$\begin{aligned} x = \frac{129^{\circ} + 71^{\circ}}{2} = \frac{200^{\circ}}{2} = 100^{\circ} \end{aligned}$
::x=129712=2002=100

Example 2
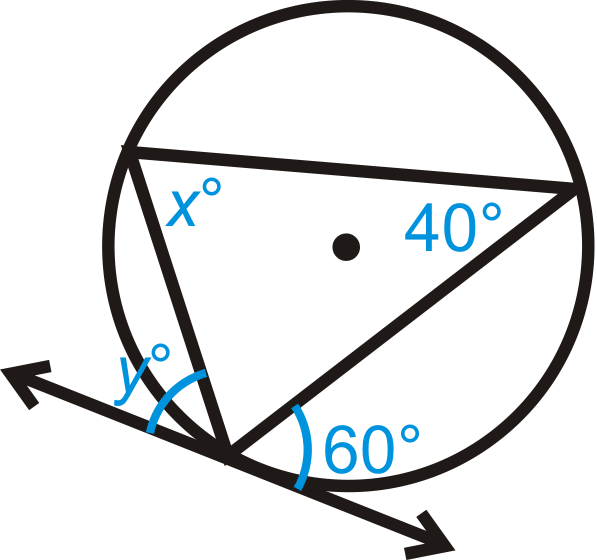
::例2

Find $\begin{aligned} x \end{aligned}$ .
::查找 x.

Use the Intersecting Chords Angle Theorem to write an equation.
::使用交叉弦角定理来写一个方程式。

$\begin{aligned} x \end{aligned}$ is supplementary to the angle that is the average of the given intercepted arcs. We call this supplementary angle $\begin{aligned} y \end{aligned}$ .
::x 是给定截取弧的平均值的角的补充。我们称之为此补充角 y 。

\begin{aligned} y = \frac{19^{\circ} + 107^{\circ}}{2} = \frac{126^{\circ}}{2} = 63^{\circ} x + 63^{\circ} = 180^{\circ}; x = 117^{\circ} \end{aligned}

::y=191072=1262=63x+63180; x=117

Example 3
::例3

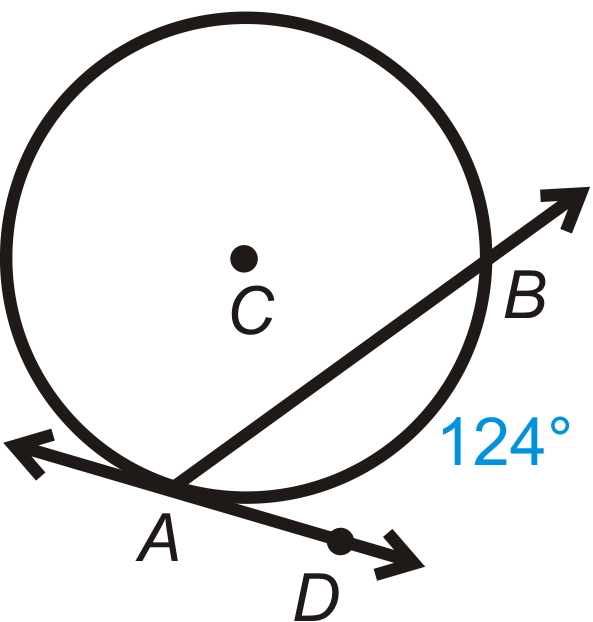
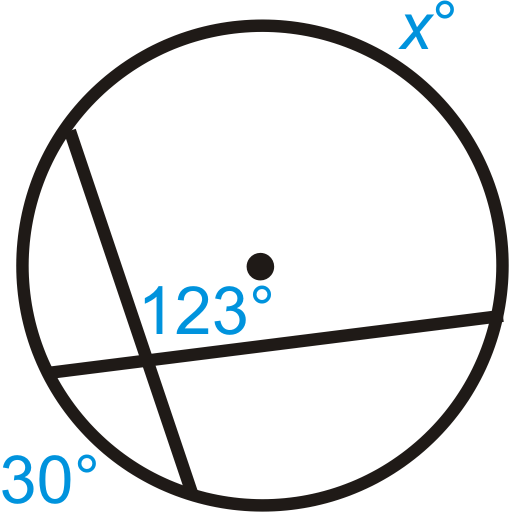
Find $\begin{aligned} m ∠ B A D \end{aligned}$ .
::去找妈妈吧

Use the Chord/Tangent Angle Theorem. $\begin{aligned} m ∠ B A D = \frac{1}{2} m \hat{A B} = \frac{1}{2} \cdot 124^{\circ} = 62^{\circ} \end{aligned}$ .
::使用弦/ 弦角定理。 mBAD=12mAB1212462。

Example 4
::例4

Find $\begin{aligned} a, b, \end{aligned}$ and $\begin{aligned} c \end{aligned}$ .
::寻找 a, b, c.

\begin{aligned} 50^{\circ} + 45^{\circ} + m ∠ a & = 180^{\circ} straight angle \\ m ∠ a & = 85^{\circ} \end{aligned}

::5045ma=180straight 角度ma=85

\begin{aligned} m ∠ b & = \frac{1}{2} \cdot m \hat{A C} \\ m \hat{A C} & = 2 \cdot m ∠ E A C = 2 \cdot 45^{\circ} = 90^{\circ} \\ m ∠ b & = \frac{1}{2} \cdot 90^{\circ} = 45^{\circ} \end{aligned}

::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

\begin{aligned} 85^{\circ} + 45^{\circ} + m ∠ c & = 180^{\circ} Triangle Sum Theorem \\ m ∠ c & = 50^{\circ} \end{aligned}

::8545mc=180Triangle 苏姆神话=50

Example 5
::例5

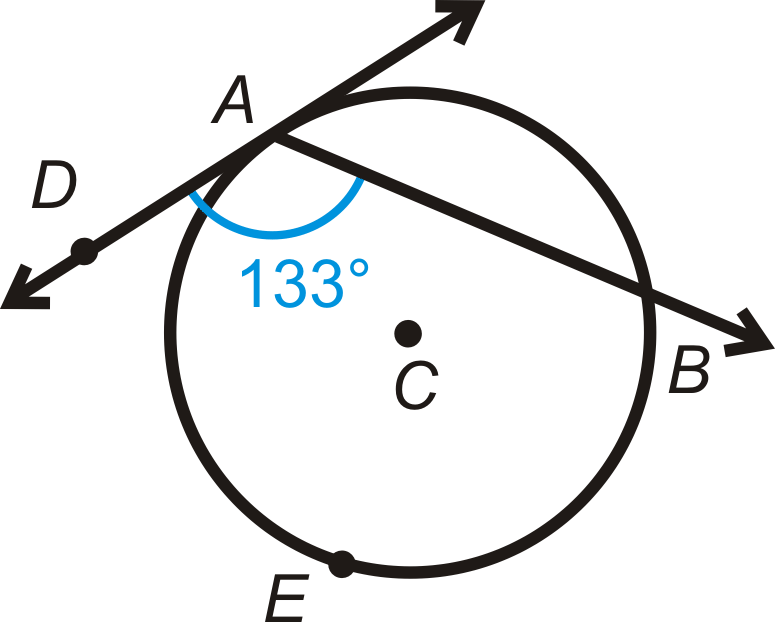
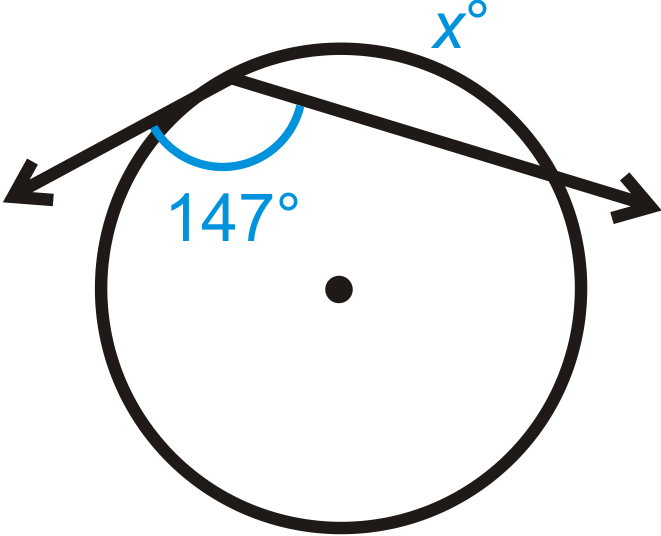
Find $\begin{aligned} m \hat{A E B} \end{aligned}$ .
::找到麦贝斯

Use the Chord/Tangent Angle Theorem. $\begin{aligned} m \hat{A E B} = 2 \cdot m ∠ D A B = 2 \cdot 133^{\circ} = 266^{\circ} \end{aligned}$ .
::使用弦/三角角定理。 mAEB2mDAB=2133266。

Review
::回顾

Find the value of the missing variable(s).
::查找缺失变量的值。

$\begin{aligned} y \neq 60^{\circ} \end{aligned}$
::60

Solve for $\begin{aligned} x \end{aligned}$ .
::解决x。

Fill in the blanks of the proof for the Intersecting Chords Angle Theorem
::填入交叉弦角定理的空格

Given : Intersecting chords $\begin{aligned} \bar{A C} \end{aligned}$ and $\begin{aligned} \bar{B D} \end{aligned}$ .
::相交和弦 AC'和BD'。

Prove : $\begin{aligned} m ∠ a = \frac{1}{2} (m \hat{D C} + m \hat{A B}) \end{aligned}$
::证明: ma=12 (mDCmAB)

*Statement*	*Reason*
1. Intersecting chords $\begin{aligned} \bar{A C} \end{aligned}$ and $\begin{aligned} \bar{B D} \end{aligned}$ .	1.
2. Draw $\begin{aligned} \bar{B C} \end{aligned}$ ::2. 绘制 BC	2. Construction
3. $\begin{aligned} m ∠ D B C & = \frac{1}{2} m \hat{D C} \\ m ∠ A C B & = \frac{1}{2} m \hat{A B} \end{aligned}$	3.
4. $\begin{aligned} m ∠ a = m ∠ D B C + m ∠ A C B \end{aligned}$	4.
5. $\begin{aligned} m ∠ a = \frac{1}{2} m \hat{D C} + \frac{1}{2} m \hat{A B} \end{aligned}$	5.

Fill in the blanks.
::填满空白。

If the vertex of an angle is _______________ a circle, then its measure is the average of the __________________ arcs.
::如果角度的顶点为 a 圆,则其测量值为弧的平均值。

If the vertex of an angle is ________ a circle, then its measure is ______________ the intercepted arc.
::如果角度的顶点是 a 圆,那么它的量度是被截取的弧。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

圆圈内外角角

Angles On and Inside a Circle ::圆圈内外角角

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)