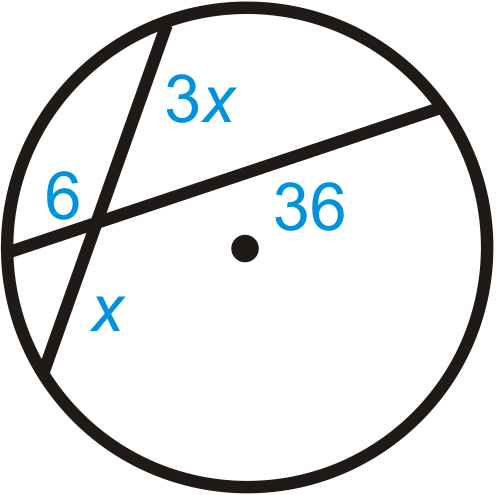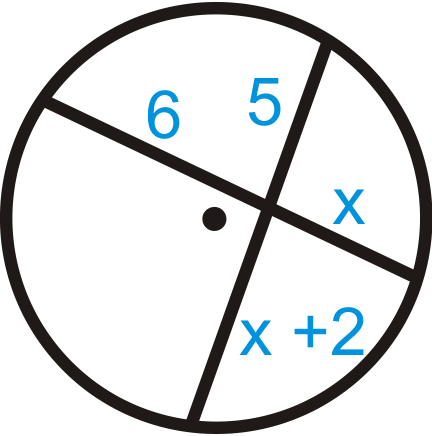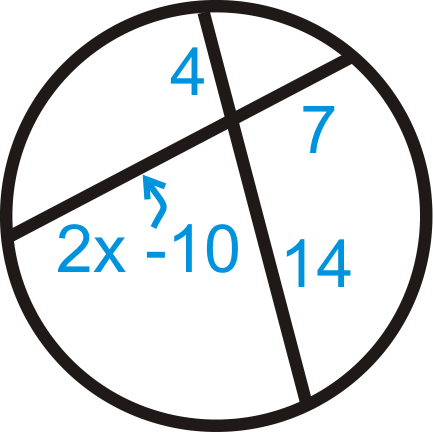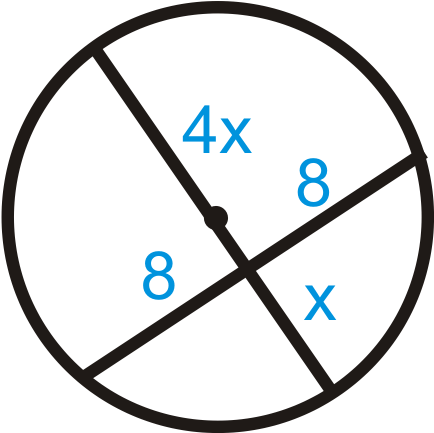9.9 弦的段数

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 来自弦的线段

  Collapse Expand

  来自弦的线段

  播放段落

  Segments from Chords
  ::来自弦的线段

  播放段落

  When we have two chords that intersect inside a circle , as shown below, the two triangles that result are similar .
  ::当我们有一个圆内的两个和弦相交时,如下文所示,结果的两个三角是相似的。

  

  播放段落

  This makes the corresponding sides in each triangle proportional and leads to a relationship between the segments of the chords, as stated in the Intersecting Chords Theorem .
  ::这就使三角形的对应边成正比,并导致弦各部分之间的关系,如交叉弦理论所述。

  播放段落

  Intersecting Chords Theorem: If two chords intersect inside a circle so that one is divided into segments of length $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ and the other into segments of length $\begin{align*}c\end{align*}$ and $\begin{align*}d\end{align*}$ then $\begin{align*}ab = cd\end{align*}$ .
  ::相交和弦理论:如果两个和弦在圆圈内相互交错,则将一个和弦分为a和b的长度部分,另一个和d的长度部分,然后是ab=cd。

  

  播放段落

  What if you were given a circle with two chords that intersect each other? How could you use the length of some of the segments formed by their intersection to determine the lengths of the unknown segments?
  ::如果给您一个圆, 加上两个交错的和弦呢? 您如何使用这些相交点所形成的部分的长度来决定未知部分的长度 ?

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

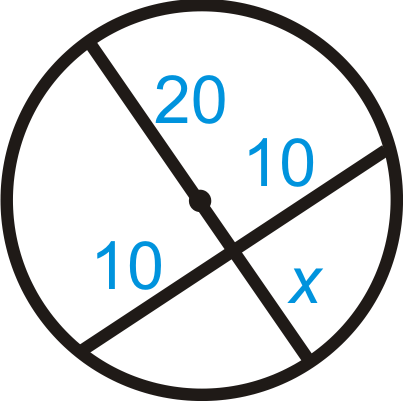
  Find $\begin{align*}x\end{align*}$ . Simplify any radicals.
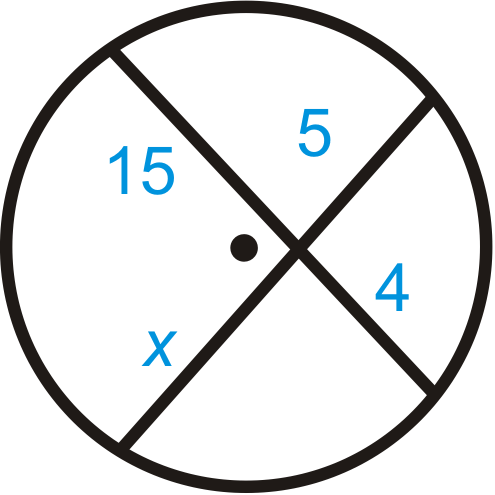
  ::查找 x. 简化任何基数 。

  

  播放段落

  Use the Intersecting Chords Theorem.
  ::使用交叉弦定理 。

  播放段落

  $$\begin{align*}15\cdot 4 &=5\cdot x\\ 60&=5x \\ x&=12\end{align*}$$
  ::154=5x60=5xxx=12

  播放段落

  Example 2
  ::例2

  播放段落

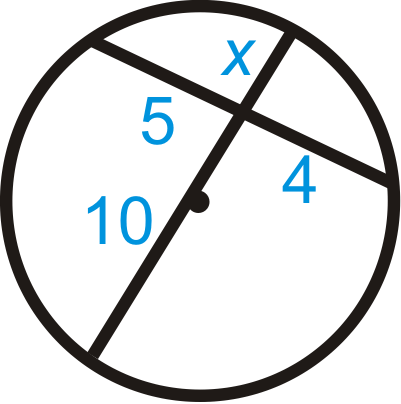
  Find  $\begin{align*}x\end{align*}$ . Simplify any radicals.
  ::查找 x. 简化任何基数 。

  

  播放段落

  Use the Intersecting Chords Theorem.
  ::使用交叉弦定理 。

  播放段落

  $$\begin{align*}18 \cdot x &=9\cdot 3\\18x &=27\\ x&=1.5\end{align*}$$
  ::18x=9318x=27x=1.5

  播放段落

  Example 3
  ::例3

  播放段落

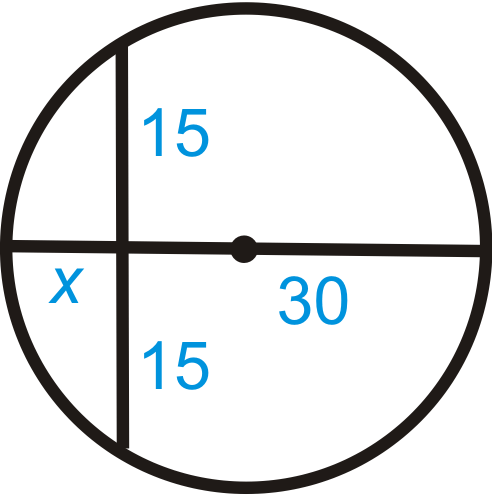
  Find $\begin{align*}x\end{align*}$ in each diagram below.
  ::在下图中查找 x。

  1. 

  播放段落

   Use the formula from the Intersecting Chords Theorem.
  ::使用来自交叉弦定理的公式 。

  播放段落

  $$\begin{align*}12 \cdot 8 &= 10 \cdot x\\ 96 &= 10x\\ 9.6 &= x\end{align*}$$
  ::128=10x96=10x9.6=x

  2. 

  播放段落

   Use the formula from the Intersecting Chords Theorem.
  ::使用来自交叉弦定理的公式 。

  播放段落

  $$\begin{align*}x \cdot 15 &= 5 \cdot 9\\ 15x &= 45\\ x &= 3\end{align*}$$
  ::x=15=5=915x=45x=3

  播放段落

  Example 4
  ::例4

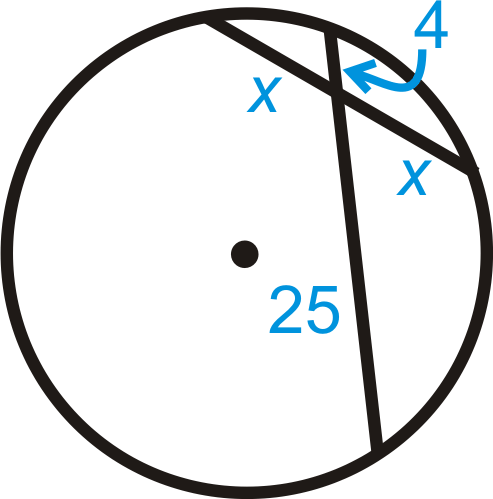
  播放段落

  Solve for $\begin{align*}x\end{align*}$  in each diagram below.
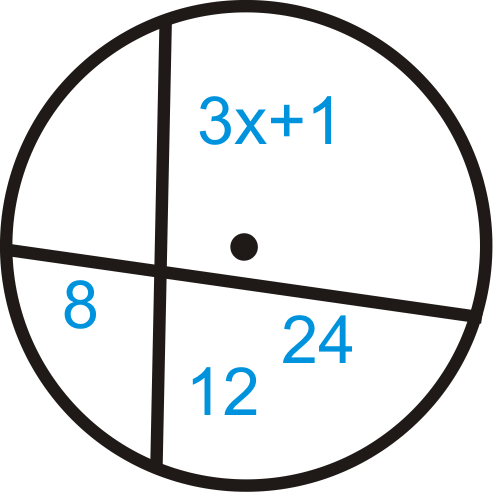
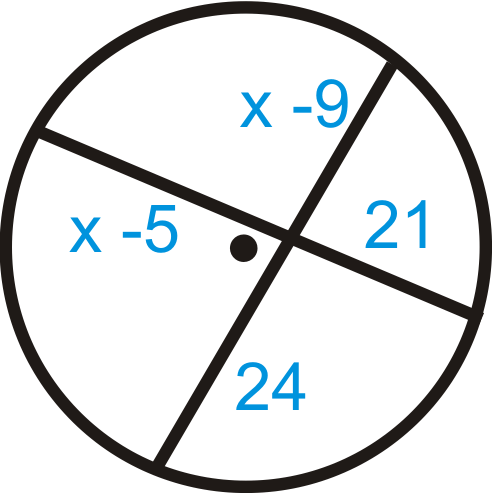
  ::在下图中为 x 解决 。

  1. 

  播放段落

   Use the Intersecting Chords Theorem.
  ::使用交叉弦定理 。

  播放段落

  $$\begin{align*}8 \cdot 24 &= (3x+1)\cdot 12\\ 192 &= 36x+12\\ 180 &= 36x\\ 5 &= x\end{align*}$$
  ::824=( 3x+1)12192=36x+12180=36x5=x

  2. 

  播放段落

   Use the Intersecting Chords Theorem.
  

  $$\begin{align*}(x-5)21 &= (x-9)24\\ 21x-105 &= 24x-216\\ 111 &= 3x\\ 37 &= x \end{align*}$$
  ::使用交叉弦定理 (x- 5) 。 (x- 9) 21= (x- 9- 9) 242421x- 105= 24x- 216111= 3x37=x

  播放段落

  Example 5
  ::例5

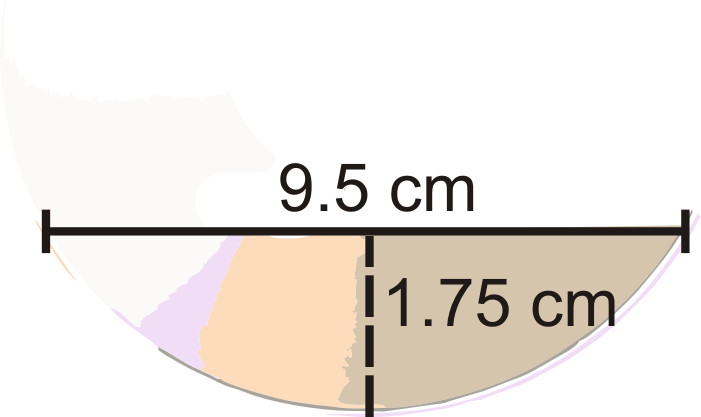
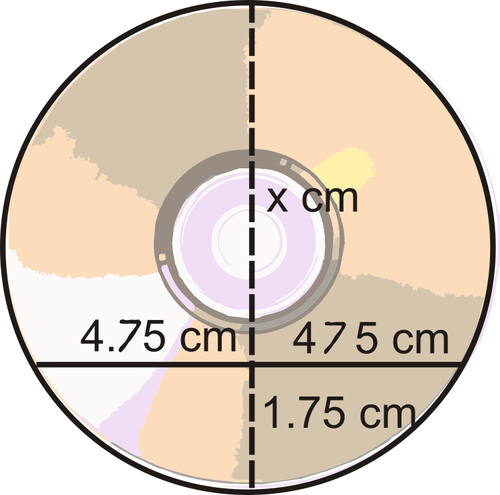
  播放段落

  Ishmael found a broken piece of a CD in his car. He places a ruler across two points on the rim, and the length of the chord is 9.5 cm. The distance from the midpoint of this chord to the nearest point on the rim is 1.75 cm. Find the diameter of the CD.
  ::Ishmael在他的车里发现了一张破碎的CD片段,他将一条尺架放在边缘两点之间,和弦的长度为9.5厘米。从这根和弦中点到最接近的边缘点的距离是1.75厘米。 找到CD的直径。

  

  播放段落

  Think of this as two chords intersecting each other. If we were to extend the 1.75 cm segment, it would be a diameter. So, if we find $\begin{align*}x\end{align*}$ in the diagram below and add it to 1.75 cm, we would find the diameter.
  ::把它想象成两个和弦相互交错。 如果我们要扩展1.75厘米段, 它会是一个直径。 所以, 如果我们在下面的图表中找到x, 并将其添加到1.75厘米, 我们就会找到直径 。

  播放段落

  $$\begin{align*}4.75 \cdot 4.75&=1.75\cdot x\\ 22.5625&=1.75x\\ x & \approx 10.3 \ cm,\ \text{making the diameter } 12.9 + 1.75 \approx \ 15 \ cm, \ \text{which is the}\\ & \qquad \qquad \qquad \text{actual diameter of a CD.}\end{align*}$$
  ::4.754.75=1.75x22.5625=1.75xx}10.3厘米,直径为12.9+1.75×15厘米,即光碟的实际直径。

  

  播放段落

  Review
  ::回顾

  播放段落

  Fill in the blanks for each problem below and then solve for the missing segment.
  ::填写下面每个问题的空白,然后解决缺失的部分。

  1. 

  播放段落

  $\begin{align*}20x=\underline{\;\;\;\;\;\;\;}\end{align*}$
  ::20x__________________________________________________________________________________________________________________

  2. 

  播放段落

  $\begin{align*}\underline{\;\;\;\;\;\;} \cdot 4=\underline{\;\;\;\;\;\;\;} \cdot x\end{align*}$
  ::4x

  播放段落

  Find $\begin{align*}x\end{align*}$ in each diagram below. Simplify any radicals.
  ::在下图中查找 x。 简化任何基数 。

  3. 
  4. 
  5. 

  播放段落

  Find the value of $\begin{align*}x\end{align*}$ .
  ::查找 x 的值。

  6. 
  7. 
  8. 
  播放段落
  9. Suzie found a piece of a broken plate. She places a ruler across two points on the rim, and the length of the chord is 6 inches. The distance from the midpoint of this chord to the nearest point on the rim is 1 inch. Find the diameter of the plate.
     ::Suzie发现了一块破碎的板块。她将一条尺架放在边缘两点之间,和弦的长度是6英寸。从这根弦的中点到最接近的边缘点的距离是1英寸。找到板块的直径。
  播放段落
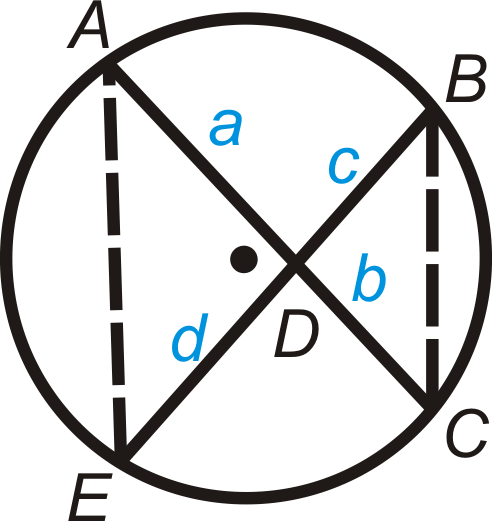
  10. Fill in the blanks of the proof of the Intersecting Chords Theorem.
      ::填满交叉弦定理的空白证据

  播放段落

  Given : Intersecting chords $\begin{align*}\overline{AC}\end{align*}$ and $\begin{align*}\overline{BE}\end{align*}$ .
  ::相交和弦 AC 和是。

  播放段落

  Prove : $\begin{align*}ab=cd\end{align*}$
  ::证明: ab=cd

  Statement	Reason
  1. Intersecting chords $\begin{align*}\overline{AC}\end{align*}$ and $\begin{align*}\overline{BE}\end{align*}$ with segments $\begin{align*}a, \ b, \ c,\end{align*}$ and $\begin{align*}d\end{align*}$ .	1.
  2.	2. Congruent Inscribed Angles Theorem
  3. $\begin{align*}\triangle ADE \sim \triangle BDC\end{align*}$	3.
  4.	4. Corresponding parts of similar triangles are proportional
  5. $\begin{align*}ab=cd\end{align*}$	5.

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。