课程： 11.8 复合固体 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节复合固体

折叠展开
复合固体
Composite Solids
::复合固体

A composite solid is a solid that is composed, or made up of, two or more solids. The solids that it is made up of are generally prisms, pyramids , cones, cylinders, and spheres. In order to find the and of a composite solid, you need to know how to find the , pyramids, cones, cylinders, and spheres. For more information on any of those specific solids, consult the concept that focuses on them. This concept will assume knowledge of those five solids.
::复合固体是由两块或更多块固体构成或构成的固体。由这些固体组成的固体通常是棱镜、金字塔、锥形、圆柱体和球体。为了找到复合固体和复合固体, 您需要知道如何找到金字塔、锥体、圆柱体和球体。要获得更多关于这些具体固体的信息, 请参考以它们为重点的概念。这个概念将假设对这五块固体的了解。

Most composite solids problems that you will see will be about volume, so most of the examples and practice problems below are about volume. There is one surface area example as well.
::您将看到的多数复合固体问题将涉及体积,所以下面的大多数实例和做法问题都涉及体积。还有一个表面积的例子。

What if you built a solid three-dimensional house model consisting of a pyramid on top of a square prism ? How could you determine how much two-dimensional and three-dimensional space that model occupies?
::如果你在平方棱柱顶上建了一个由金字塔组成的坚固的三维房屋模型呢? 你怎么能确定该模型占据了多少二维和三维空间呢?

Examples
::实例

Example 1
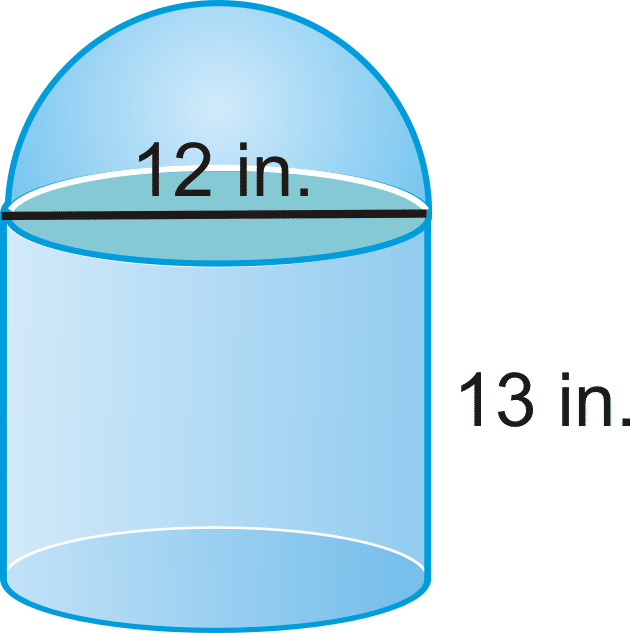
::例1

Find the volume of the following solid.
::查找以下固体的体积。

Use what you know about cylinders and spheres. The top of the solid is a hemisphere.
::使用你所知道的圆柱体和球体。固体的顶部是一个半球。

$\begin{aligned} V_{c y l i n d e r} & = π 6^{2} (13) = 468 π \\ V_{h e m i s p h e r e} & = \frac{1}{2} (\frac{4}{3} π 6^{3}) = 144 π \\ V_{t o t a l} & = 468 π + 144 π = 612 π i n^{3} \end{aligned}$
$\begin{align*}V_{cylinder} &= \pi 6^2 (13)=468 \pi\\ V_{hemisphere} &= \frac{1}{2} \left(\frac{4}{3} \pi 6^3\right)=144 \pi\\ V_{total} &= 468 \pi+144 \pi =612 \pi \ in^3\end{align*}$
::Vcylinder62(13)=468-Vhemisphere=12(43-1963)=144-Vtl=4681446123英寸

Example 2
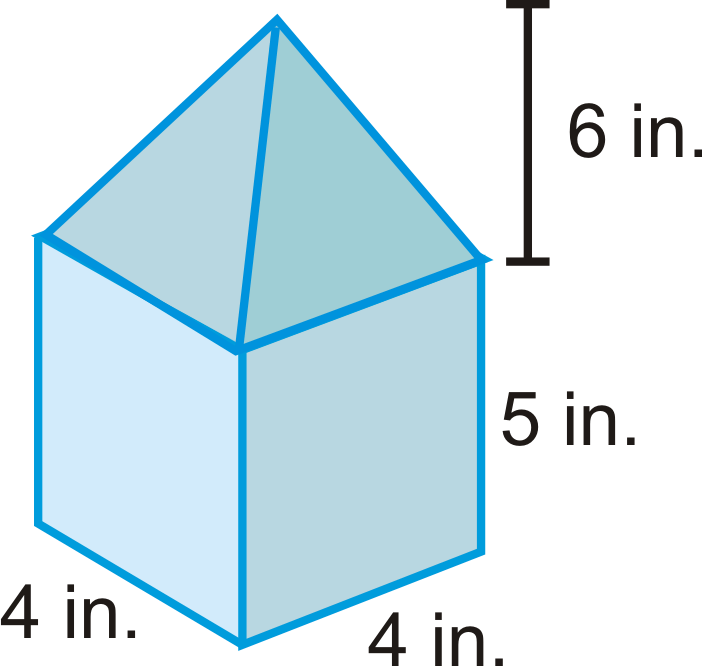
::例2

Find the volume of the base prism. Round your answer to the nearest hundredth.
::查找底基棱晶的量。将您的答复转至最接近的百分百。

Use what you know about prisms.
::利用你对棱镜的了解

$\begin{aligned} V_{p r i s m} & = B \cdot h \\ V_{p r i s m} & = (4 \cdot 4) \cdot 5 \\ V_{p r i s m} & = 80 i n^{3} \end{aligned}$
$\begin{align*}V_{prism}&=B \cdot h \\ V_{prism}&=(4\cdot 4)\cdot 5\\ V_{prism}&=80in^3\end{align*}$
::Vprism=BähVprism=( 44) =5Vprism=80in3

Example 3
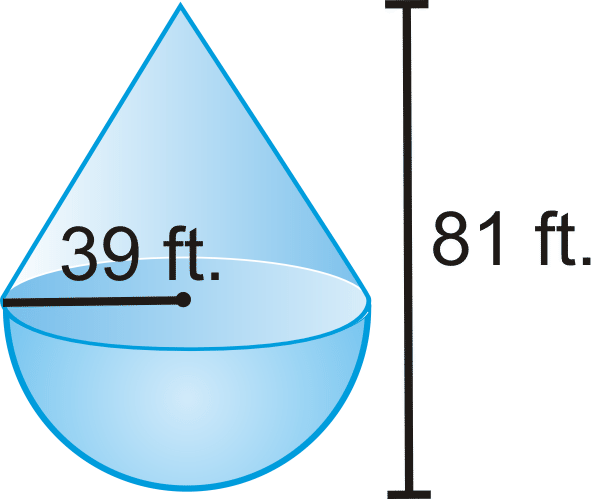
::例3

Find the volume of the solid below.
::查找以下固体的体积。

This solid is a parallelogram-based prism with a cylinder cut out of the middle.
::这个固体是一个平行图基棱镜, 中间有一个圆柱体被切开。

$\begin{aligned} V_{p r i s m} & = (25 \cdot 25) 30 = 18, 750 c m^{3} \\ V_{c y l i n d e r} & = π (4)^{2} (30) = 480 π c m^{3} \end{aligned}$
$\begin{align*}V_{prism} &= (25 \cdot 25)30=18,750 \ cm^3\\ V_{cylinder} &= \pi (4)^2 (30)=480 \pi \ cm^3\end{align*}$
::Vprism=( 25_ 25_ 25)30=18 750 cm3Vcylinder(4)( 2( 30) = 480 cm3

The total volume is $\begin{align*}18750 - 480 \pi \approx 17,242.04 \ cm^3\end{align*}$ .
::总量为18750 - 480 17,242.04 立方厘米。

Example 4
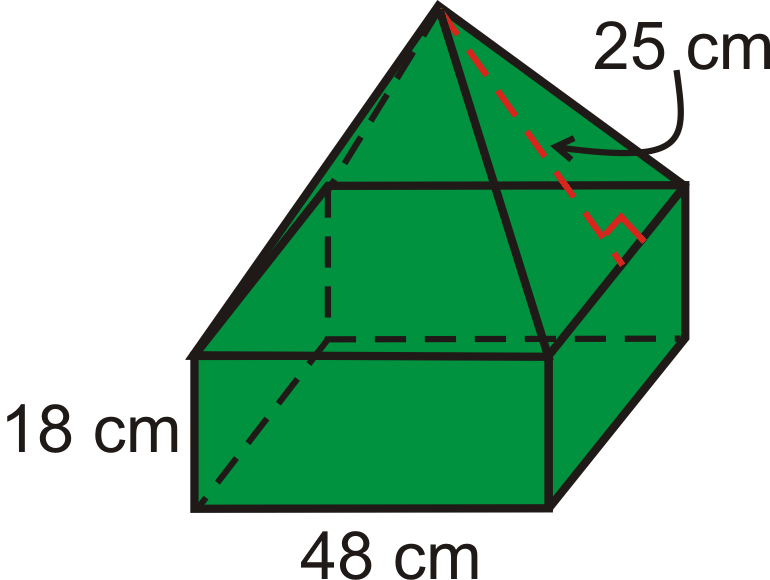
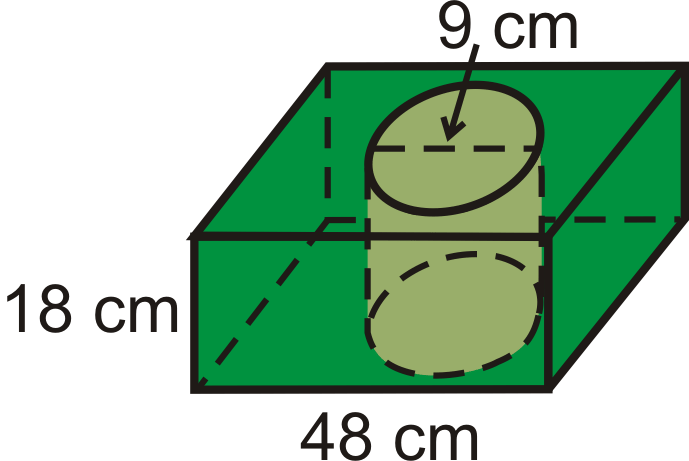
::例4

Find the volume of the composite solid. All bases are squares.
::查找复合固体的体积。所有基座都是方形的。

This is a square prism with a square pyramid on top. First, we need the height of the pyramid portion. Using the Pythagorean Theorem , we have, $\begin{align*}h=\sqrt{25^2-24^2}=7\end{align*}$ .
::这是一个方形棱镜, 上面是方形金字塔。首先, 我们需要金字塔部分的高度。使用 Pytagoren Theorem, 我们有, h=252 - 242=7 。

$\begin{aligned} V_{p r i s m} & = (48) (48) (18) = 41, 472 c m^{3} \\ V_{p y r a m i d} & = \frac{1}{3} (48^{2}) (7) = 5376 c m^{3} \end{aligned}$
$\begin{align*}V_{prism} &= (48)(48)(18)=41,472 \ cm^3\\ V_{pyramid} &= \frac{1}{3} (48^2)(7)=5376 \ cm^3\end{align*}$
::Vprism=(48)(48)(18)=41,472cm3Vpyrarmid=13(482)(7)=5376cm3

The total volume is $\begin{align*}41,472 + 5376 = 46,848 \ cm^3\end{align*}$ .
::总量为41,472+5376=46,848立方厘米。

Example 5
::例5

Find the surface area of the following solid.
::查找以下固体的表面面积。

This solid is a cylinder with a hemisphere on top. It is one solid, so do not include the bottom of the hemisphere or the top of the cylinder.
::这是一个圆柱体, 上面有一个半球。它是一个固体, 所以不包含半球的底部或圆柱体的顶部。

$\begin{aligned} S A & = L A_{c y l i n d e r} + L A_{h e m i s p h e r e} + A_{b a s e c i r c l e} \\ = 2 π r h + \frac{1}{2} 4 π r^{2} + π r^{2} \\ = 2 π (6) (13) + 2 π 6^{2} + π 6^{2} \\ = 156 π + 72 π + 36 π \\ = 264 π i n^{2} \end{aligned}$
$\begin{align*}SA &=LA_{cylinder}+LA_{hemisphere}+A_{base \ circle}\\ &= 2 \pi rh+\frac{1}{2} 4 \pi r^2+\pi r^2\\ &= 2 \pi (6)(13)+2 \pi 6^2+\pi 6^2\\ &= 156 \pi +72 \pi +36 \pi\\ &= 264 \pi \ in^2 \qquad \qquad \end{align*}$
::SA=LAAcylinder+LAHemisphere+基础圆=2rh+124r2r2=2(6)(13)+26262=1567236264英寸

“LA” stands for lateral area .
::“LA”代表横向地区。

Review
::回顾

Round your answers to the nearest hundredth. The solid below is a cube with a cone cut out.
::返回最近的第一百个答案。下面的固体是圆锥形的立方体,切开圆锥形。

Find the volume of the cube.
::查找立方体的音量。

Find the volume of the cone.
::找到锥体的体积。

Find the volume of the entire solid.
::找到整个固体的体积

The solid below is a cylinder with a cone on top.
::下面的固体是一个圆柱体,上面有一个圆锥。

Find the volume of the cylinder.
::找到气瓶的体积。

Find the volume of the cone.
::找到锥体的体积。

Find the volume of the entire solid.
::找到整个固体的体积

Find the volume of the following shapes. Round your answers to the nearest hundredth.
::查找以下形状的音量。将您的答案绕到最近的一百位。

(Note: You may assume the bottom is open.)
:注:你可以假定底部是开着的。 )

A sphere has a radius of 5 cm. A right cylinder has the same radius and volume. Find the height of the cylinder.
::球体半径为 5 厘米。右圆柱体的半径和体积相同。查找圆柱体的高度。

The bases of the prism are squares and a cylinder is cut out of the center. Keep your answers in terms of $\begin{align*}\pi\end{align*}$ if needed.
::棱晶的底部是正方形, 一个圆柱体被切出中心。如果需要, 请保留您的回答。

Find the volume of the prism.
::寻找棱镜的体积。

Find the volume of the cylinder in the center.
::在中间找到圆柱体的体积。

Find the volume of the figure.
::查找数字的音量。

This is a prism with half a cylinder on the top. Keep your answers in terms of $\begin{align*}\pi\end{align*}$ if needed.
::这是一个有半个圆柱的棱镜, 上面有半个圆柱。如果需要, 请保留您的回答。

Find the volume of the prism.
::寻找棱镜的体积。

Find the volume of the half-cylinder.
::找到半气缸的体积

Find the volume of the entire figure.
::查找整个数字的音量。

Tennis balls with a 3 inch diameter are sold in cans of three. The can is a cylinder. Round your answers to the nearest hundredth.
::直径为3英寸的网球以3英寸的罐子出售。罐头是一个圆筒。将答案绕到最近的一百个答案。

What is the volume of one tennis ball?
::一个网球的体积是多少?

What is the volume of the cylinder?
::气瓶的体积是多少?

Assume the balls touch the can on the sides, top and bottom. What is the volume of the space not occupied by the tennis balls?
::假设球在侧面、顶部和底部触摸罐子。网球没有占用的空间的体积是多少?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

复合固体

Composite Solids ::复合固体

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Composite Solids
::复合固体

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)