课程： 2.9 寻找职能的领域和范围

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节查找函数的域和范围

折叠展开
查找函数的域和范围
You just got a new part-time job at the mall that pays a base rate of $150/week plus $5/sale. Your boss encourages you to make as many sales as possible but she will cap your weekly earnings at $250. What are the domain and range of the function represented by this situation?
::你刚在商场找到一份新的兼职工作,支付每星期150美元加5美元的基本费率。你的老板鼓励你尽可能多地销售,但她会将每周收入限制在250美元。这种情况所代表的职能的域域和范围是什么?

Domain and Range of a Function
::函数的域域和范围

The input and output of a function is also called the domain and range. The domain of a function is the set of all input values. The range of a function is the set of all output values. Sometimes, a function is a set of points. In this case, the domain is all the $\begin{aligned} x - \end{aligned}$ values and the range is all the $\begin{aligned} y - \end{aligned}$ values. Functions can also be linear and polynomial equations. In these instances, you need to graph the function to see where it is defined. You may notice that some functions are defined for “all real numbers.” The symbol, $\begin{aligned} R \end{aligned}$ , is used to denote the set of all real numbers.
::函数的输入和输出也被称为域和范围。函数的域是所有输入值的一组。函数的范围是所有输出值的一组。函数的范围是所有输出值的一组。有时,函数是一组点。在这种情况下,域是全部 x- 值,范围是全部 y- 值。函数也可以是线性方程和多义方程。在这种情况下,您需要绘制函数的图形,以查看它被定义的位置。您可能注意到,有些函数被定义为“所有真实数字”。符号R用来表示所有真实数字的一组。

Let's determine if {(9, 2), (7, -3), (4, -6), (-10, 4), (-2, -7)} is a function. If so, we will find the domain and range.
::让我们确定{( 9, 2) 、 (7, 3) 、 (4, 6) 、 (10, 4) 、 (2, 7) 是否是一个函数。如果是这样, 我们将找到域和范围。

First, this is a function because the $\begin{aligned} x - \end{aligned}$ values do not repeat. To find the domain, we need to list all the $\begin{aligned} x - \end{aligned}$ values. The range is all the $\begin{aligned} y - \end{aligned}$ values. Typically, you would list the values in the order they appear. Notice the notation.
::首先,这是一个函数, 因为 x - 值不重复。要找到域, 我们需要列出所有 x - 值。范围是全部 y - 值。通常, 您会按其出现的顺序列出数值。注意标记。

$\begin{aligned} x \in {9, 7, 4, - 10, - 2} \\ y \in {2, - 3, - 6, 4, - 7} \end{aligned}$

::x9,7,4,4-10,-2,2,3,6,4-7}

The $\begin{aligned} \in \end{aligned}$ symbol means “an element of/in.” The braces, { }, around the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ values, indicate that each is a set. In words, you would say, “ $\begin{aligned} x \end{aligned}$ is an element in the set 9, 7, 4, -10, and 2.” Depending on the text, you may see “:” (colon) interchanged with the “ $\begin{aligned} \in \end{aligned}$ ” symbol and sets without { } around them.
::“% ” 符号指“ 元素/ 英寸 ” 。在 x 和 y- value 周围的括号 , {} 和 y- value 表示每个符号都是一组。换句话说, 您会说 , “ x 是 9 、 7 、 4 、 10 和 2 集中的一个元素。 ” 根据文字, 您可以看到“ ” ( 结号) 与“ { ” 符号和组群互换, 周围没有 { } 。

Let's find the domain and range for the following problems.
::让我们为以下问题找到域域和范围。

$\begin{aligned} y = x - 3 \end{aligned}$
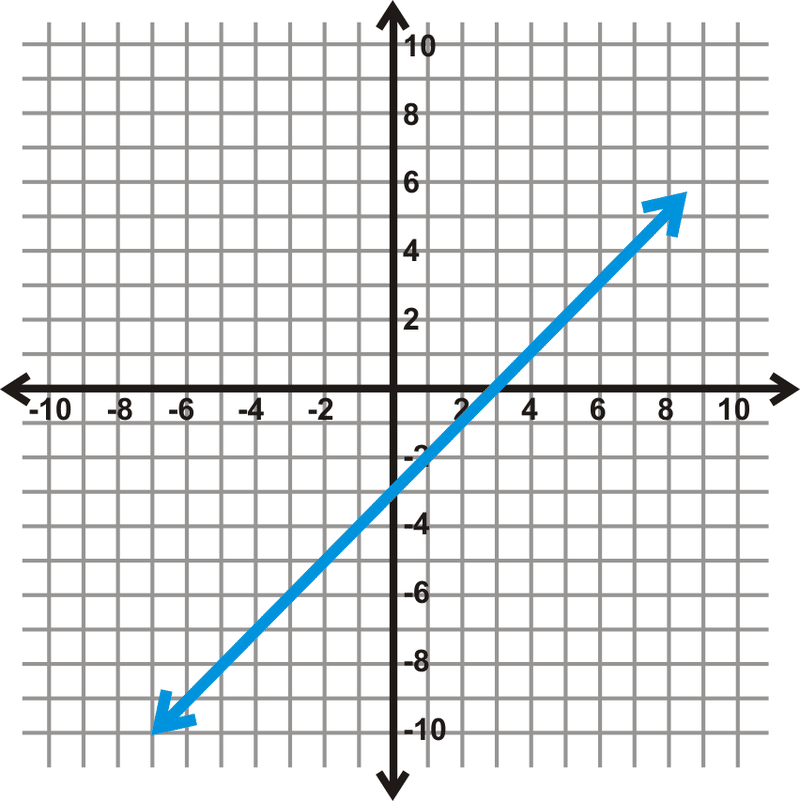
::y=x-3 y=x-3

Because this is a linear equation we also know that it is a linear function . All lines continue forever in both directions, as indicated by the arrows.
::因为这是一个线性方程式, 我们也知道这是一个线性函数。正如箭头所显示的, 所有线条都永远在双向中持续。

Notice the line is solid, there are no dashes or breaks. This means that it is continuous . A continuous function has a value for every $\begin{aligned} x \end{aligned}$ , or the domain is all real numbers. Can you plug in ANY value for $\begin{aligned} x \end{aligned}$ and get a $\begin{aligned} y - \end{aligned}$ value? Yes. There are a few ways to write this.
::注意线是固态的, 没有破折号或折号。这意味着它是连续的。连续函数对每个 x 都有值, 或域是全部真实数字。您可以插入 x 的任意值并获得 Y - 值吗 ? 是的。有几种方法可以写入它。

Domain : $\begin{aligned} x \in R \end{aligned}$ , $\begin{aligned} x \in (- \infty, \infty) \end{aligned}$ , $\begin{aligned} x \end{aligned}$ is all reals
::域 : xR, x(,,), x 是全部真实的

In words, $\begin{aligned} x \end{aligned}$ is an element in the set of real numbers.
::换句话说,x是一组真实数字中的一个元素。

The second option, $\begin{aligned} (- \infty, \infty) \end{aligned}$ , is an interval, not a point. The parenthesis indicate that infinity, $\begin{aligned} \infty \end{aligned}$ , and negative infinity, $\begin{aligned} - \infty \end{aligned}$ , are not included in the interval, but every number between them is. To include an endpoint in the interval, use [ or ] brackets . This is called interval notation.
::第二个选项, (, ) 是一个间隔, 不是点。括号表示无穷无尽, 和负无穷无穷, , , , 不包含在间隔内, 但它们之间的每个数字都是。要在间隔内包括一个终点, 请使用 [ 括号括号。这称为间隙标记。

The range of this function is also continuous. Therefore , the range is also the set of all real numbers. We can write the range in the same ways we wrote the domain, but with $\begin{aligned} y \end{aligned}$ instead of $\begin{aligned} x \end{aligned}$ .
::此函数的范围也是连续的。因此, 此范围也是所有实际数字的一组。我们可以以我们写域时的相同方式写出该区域, 但是用 y 而不是 x 来写。

Range : $\begin{aligned} y \in R \end{aligned}$ or $\begin{aligned} y \in (- \infty, \infty) \end{aligned}$
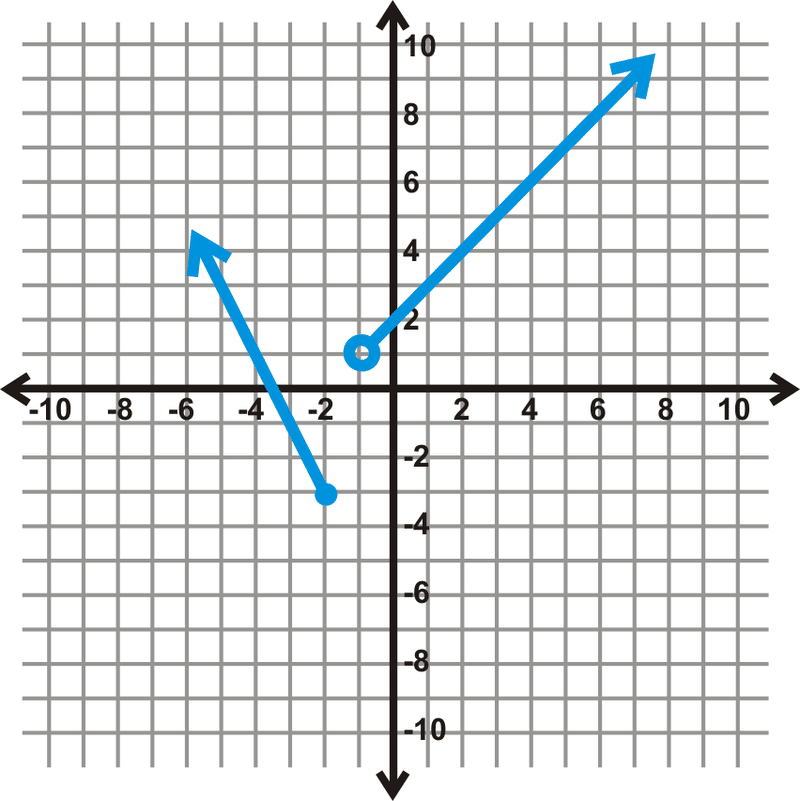
::范围:yR或y(,)

This is a function, even though it might not look like it. This type of function is called a piecewise function because it pieces together two or more parts of other functions.
::这是一个函数, 即使它看起来可能不像它。这种类型的函数被称为按片函数, 因为它将其它函数的两个或两个以上部分一起折叠在一起。

To find the domain, look at the possible $\begin{aligned} x - \end{aligned}$ values. Notice that when $\begin{aligned} x \end{aligned}$ is between -2 and -1 it is not defined, or there are no $\begin{aligned} x - \end{aligned}$ values.
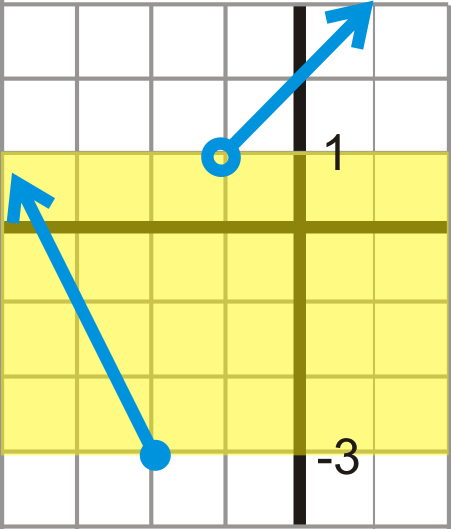
::要查找域, 请查看可能的 x - 值。注意当 x 在 - 2 和 - 1 之间时, 它没有定义, 或者没有 x - 值。

Mathematically, this would be written: $\begin{aligned} x \in (- \infty, - 2] \cup (- 1, \infty) \end{aligned}$ . The $\begin{aligned} \cup \end{aligned}$ symbol means “ union .” In words, the domain is “all real numbers except those between -2 and -1.” Notice that -2 is included in the domain because the dot at -2 is closed. To find the range, we need to look at the possible $\begin{aligned} y - \end{aligned}$ values. Changing our viewpoint to look at the $\begin{aligned} y - \end{aligned}$ axis, at first glance, it looks like the function is not defined from 1 to -3.
::从数学角度讲,这将写成: x(, , -2, , )    ) (  )      ) )  ) )    ) )                                                           

However, upon further investigation, the branch on the left does pass through the yellow region, where we though the function was not defined. This means that the function is defined between 1 and -3 and thus for all real numbers. However, below -3, there are no $\begin{aligned} y - \end{aligned}$ values. The range is $\begin{aligned} y \in [- 3, \infty) \end{aligned}$ .
::然而,经过进一步调查,左侧的分支确实穿过黄色区域,我们看这个功能没有定义,这意味着该功能在1-3之间,因此对所有实际数字都有定义。然而,在-3之下,没有y-values,范围是y[-3,]。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the domain and range of the function of your sales, where you make a base rate of $150/week plus $5/sale (your weekly earnings are capped at $250/week).
::早些时候,有人要求你找到销售功能的域域和范围,基本费率为150美元/周加5美元/销售(每周收入上限为250美元/周)。

The function represented by this situation can be written as $\begin{aligned} y = 150 + 5 x \end{aligned}$ , where x is the number of sales you make. You can't make a negative number of sales, so the least amount of sales you can make is zero. To find the maximum number of sales before you reach the cap, we must plug in $250 for y .
::此情形所代表的函数可以以 y=150+5x 写成, 其中 x 是您所做的销售数量。您不能做负数的销售, 所以最小的销售量是零。要在您达到上限之前找到最大销售量, 我们必须插入 250 美元。

$\begin{aligned} 250 = 150 + 5 x \\ 100 = 5 x \\ x = 20 \end{aligned}$

::250=150+5x100=5xxx=20

Therefore, the domain of the function is $\begin{aligned} 0 \leq x \leq 20 \end{aligned}$ .
::因此,该功能的域为 0xx%20 。

To find the range, plug the two extremes of the domain into the equation . When x equals 0, y equals 150, and when x equals 20, y equals 250.
::要找到范围, 请在方程中插入域的两个极端。当 x 等于 0 时, y 等于 150, 当 x 等于 20 时, y 等于 250 。

Therefore the range of the function is $\begin{aligned} 150 \leq y \leq 250 \end{aligned}$ .
::因此,该职能的范围是150y250。

Example 2
::例2

Find the domain and range of the following function: {(8, 3), (-4, 2), (-6, 1), (5, 7)}.
::查找下列函数的域和范围:{(8),3,(4,2),(6,1),(5,7)}。

Domain: $\begin{aligned} x \in {8, - 4, - 6, 5} \end{aligned}$ Range: $\begin{aligned} y \in {3, 2, 1, 7} \end{aligned}$
::域 : x8, - 4, - 6,5} 范围 : y 3, 2, 1,7}

Example 3
::例3

Find the domain and range of the following function: $\begin{aligned} y = - \frac{1}{2} x + 4 \end{aligned}$ .
::查找以下函数的域和范围: y12x+4。

Domain: $\begin{aligned} x \in R \end{aligned}$ Range: $\begin{aligned} y \in R \end{aligned}$
::域 : xR 范围 : yR

Example 4
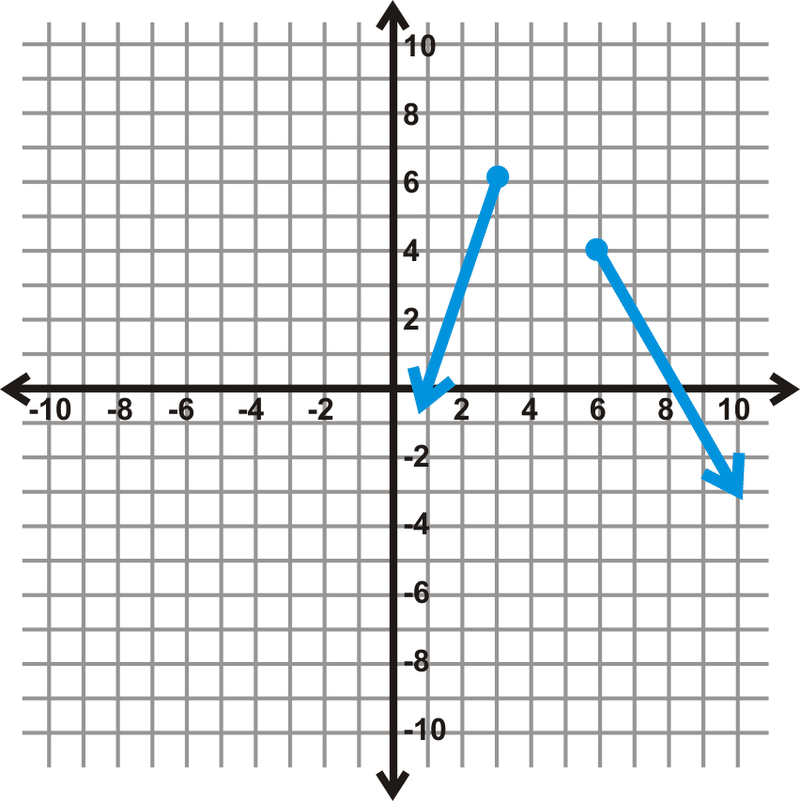
::例4

Find the domain and range of the following function.
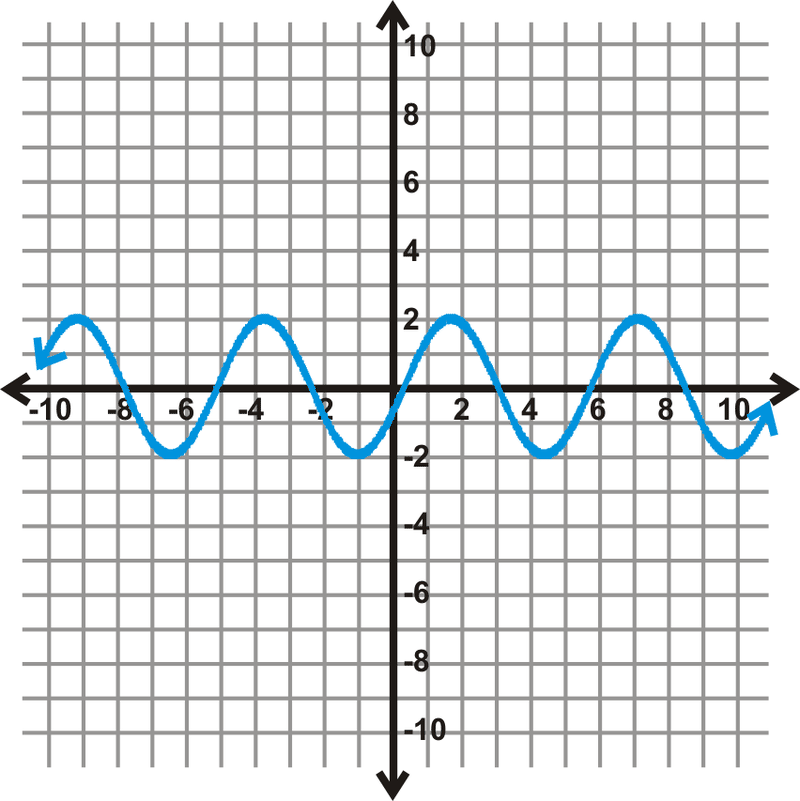
::查找下列函数的域和范围。

This is a piecewise function. The $\begin{aligned} x - \end{aligned}$ values are not defined from -2 to 1. The range looks like it is not defined from 1 to 7, but the lines continue on, filling in that space as $\begin{aligned} x \end{aligned}$ gets larger, both negatively and positively.
::这是一个片段函数。 x - 值没有定义从 - 2 到 1. 。范围看起来似乎没有定义从 1 到 7, 但线条会继续, 当 x 变大时填充该空格, 无论是负的还是正的。

Domain: $\begin{aligned} x \in (- \infty, - 2) \cup (1, \infty) \end{aligned}$ Range: $\begin{aligned} y \in R \end{aligned}$
::域 : x (1, ) 范围 : yR

Example 5
::例5

Find the domain and range of the following function.
::查找下列函数的域和范围。

This is a parabola , the graph of a quadratic equation . Even though it might not look like it, the ends of the graph continue up, infinitely, and $\begin{aligned} x \end{aligned}$ keeps growing. In other words, $\begin{aligned} x \end{aligned}$ is not limited to be between -9 and 5. It is all real numbers. The range, however, seems to start at -6 and is all real numbers above that value.
::这是一个抛物线, 一个二次方程的图形。尽管它看起来可能不像它, 图表的结尾会无限地继续上升, x 还在不断增长。换句话说, x 不局限于 - 9 和 5 之间, 它都是真实的数字。然而, 范围似乎从 - 6 开始, 并且都是高于该数值的真实数字。

Domain: $\begin{aligned} x \in R \end{aligned}$ Range: $\begin{aligned} y \in [- 6, \infty) \end{aligned}$
::域 : xR 范围 : y[- 6, ]

Review
::回顾

Determine if the following sets of points are functions. If so, state the domain and range.
::确定以下各组点是否为函数。如果是,请说明域和范围。

{(5, 6), (-1, 5), (7, -3), (0, 9)}

{(9, 8), (-7, 8), (-7, 9), (8, 8)}

{(6, 2), (-5, 6), (-5, 2)}

{(-1, 2), (-6, 3), (10, 7), (8, 11)}

{(5, 7), (3, 7), (5, 8), (8, 1)}

{(-3, -4), (-5, -6), (1, 2), (2, -6)}

Find the domain and range of the following functions.
::查找下列函数的域和范围。

$\begin{aligned} y = 3 x - 7 \end{aligned}$
::y=3x-7 y=3x-7

$\begin{aligned} 6 x - 2 y = 10 \end{aligned}$
::6--2y=10

Challenge
::挑战挑战挑战挑战

Writing Make a general statement about the domain and range of all linear functions. Use the proper notation.
::写入关于所有线性函数的域和范围的普通语句。使用正确的符号。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

查找函数的域和范围

Domain and Range of a Function ::函数的域域和范围

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Domain and Range of a Function
::函数的域域和范围

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)