Course: 2.13 使用普通绝对值平方和图形计算器

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 使用普通绝对值平方和图形计算器

Collapse Expand
使用普通绝对值平方和图形计算器
Mrs. Patel assigns the absolute value function $\begin{aligned} y = - | x + 3 | - 2 \end{aligned}$ . She tells her students to find the vertex .
::Patel夫人指定了绝对值函数 yx+32. 她叫学生们找到顶点。

"This is hard," George laments. "I'm going to need a calculator."
::"这很难" 乔治哀叹 "我需要计算器"

"No, it's not," Sarai counters. "I can tell you what the vertex is without even graphing by hand."
::"不,不是的,"Sarai对数。" "我可以告诉你什么是顶端,不用手工绘制图表。"

Who is right and what is the vertex?
::谁是对的,什么是顶部?

General Form of an Absolute Value Function
::绝对值函数的一般形式

We were already introduced to the general equation of an absolute value function. Let’s formally define it here.
::我们已经被引入了绝对价值函数的一般等式。让我们在这里正式定义它。

General Form of an Absolute Value Function : For any absolute value function, the general form is $\begin{aligned} y = a | x - h | + k \end{aligned}$ , where $\begin{aligned} a \end{aligned}$ controls the width of the “V” and $\begin{aligned} (h, k) \end{aligned}$ is the vertex.
::绝对值函数的一般形式:对于任何绝对值函数,一般形式为y=ax-hk,其中控制“V”和(h,k)的宽度为顶点。

You probably made these connections already, but now we will put it all to use together.
::你可能已经建立这些联系了但现在我们把这些都用到一起了

Let's graph $\begin{aligned} y = | x | \end{aligned}$ , $\begin{aligned} y = \frac{1}{2} | x | \end{aligned}$ , and $\begin{aligned} y = 2 | x | \end{aligned}$ on the same set of axes and compare the three functions.
::让我们在同一组轴上绘制 yx, y=12x, y=2x, 比较三个函数。

You can make a table for all three of these functions. However, now that we have a better understanding of absolute value functions, let’s use some patterns. First, look at the vertex. Nothing is being added or subtracted, so the vertex for all three will be (0, 0). Second, look at “ $\begin{aligned} a \end{aligned}$ .” For an absolute value function, we can think of a like the . Referring back to the definition of the parent graph , each function above can be rewritten as:
::您可以为上述所有三个函数制成一张表格。但是, 既然我们对绝对值函数有了更好的理解, 让我们使用一些模式。首先, 看看顶点。没有增加或减去任何东西, 所以所有三个函数的顶点都将是 0, 0 。其次, 看看“ a ” 。对于一个绝对值函数, 我们可以想出一个类似。回顾父图的定义, 以上每个函数都可以被重写为 :

$\begin{aligned} y = {\begin{cases} x; x \geq 0 \\ - x; x < 0 \end{cases} (blue), y = {\begin{cases} \frac{1}{2} x; x \geq 0 \\ - \frac{1}{2} x; x < 0 \end{cases} (red), and y = {\begin{cases} 2 x; x \geq 0 \\ - 2 x; x < 0 \end{cases} (green) \end{aligned}$

::yx; x0- x; x < 0( 蓝色) y% 12x; x0- 12x; x < 0( 红色) 和 y2x; x0- 2x; x < 0( 绿色)

Comparing the three, we see that if the slope is between 1 and 0, the opening is wider than the parent graph. If the slope, or $\begin{aligned} a \end{aligned}$ , is greater than 1, then that opening is narrower. The amount of the opening between the two sides of an absolute value function (and other functions) is called the breadth .
::比较这三个数值,我们看到,如果斜坡在1到0之间,打开的宽度大于母图。如果斜坡或 a大于1,那么打开的宽度较小。绝对值函数(和其他函数)两侧之间的开口量称为宽度。

Now, in addition to drawing a table, we can use the general form of an absolute value equation and the value of $\begin{aligned} a \end{aligned}$ to find the shape of the $\begin{aligned} V \end{aligned}$ .
::现在,除了绘制表格之外,我们还可以使用绝对值方程的一般形式和a的价值来找到V的形状。

Without making a table, let's sketch the graph of $\begin{aligned} y = - | x - 6 | - 2 \end{aligned}$ .
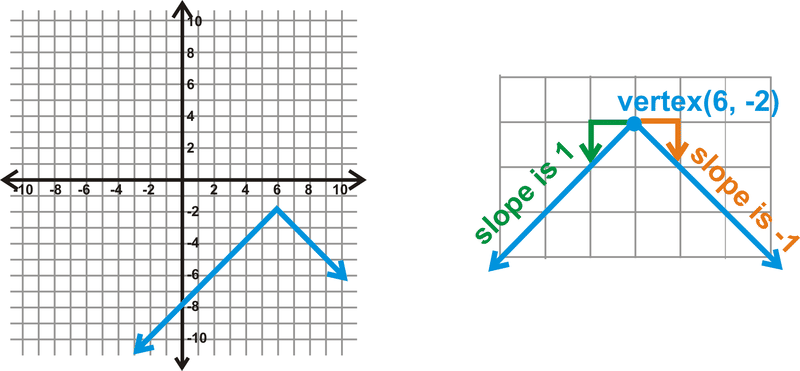
::在不做表的情况下,让我们绘制一下 yx -62的图表。

First, determine the vertex. From the general form, we know that it will be (6, -2). Notice that the $\begin{aligned} x - \end{aligned}$ variable is the opposite sign of what is in the equation; the $\begin{aligned} y - \end{aligned}$ variable is the same. That is our starting point . Then, we have a negative sign in front of the absolute value. This means our $\begin{aligned} V \end{aligned}$ will open down. Finally, there is no $\begin{aligned} a \end{aligned}$ term , so we can assume it is 1, meaning that the slope of each side of the $\begin{aligned} V \end{aligned}$ will be 1 and -1.
::首先, 确定顶点。从一般形式中, 我们知道它将会是 (6, - 2) 。注意 x- 变量是方程中的相反符号; y - 变量是相同的。这是我们的起点。然后, 我们的绝对值前面有一个负面符号。这意味着 V 将打开。最后, 没有术语, 因此我们可以假设它是 1 , 意味着 V 的两侧的斜坡将是 1 和 - 1 。

Lastly, we can use a graphing calculator to help us graph . The directions given here pertain to the TI-83/84 series; however every graphing calculator should be able to graph absolute value functions.
::最后,我们可以使用图表计算器来帮助我们绘制图表。这里给出的方向与TI-83/84系列有关;然而,每个图形计算器都应该能够绘制绝对值函数的图表。

Now, let's use a graphing calculator to graph $\begin{aligned} y = | 4 x + 1 | - 2 \end{aligned}$ . Find the vertex, domain , and range .
::现在,让我们使用图形计算器来绘制 y4x+12。找到顶点、域和范围。

For the TI-83/84
::用于TI-83/84

Step 1: Press the $\begin{aligned} Y = \end{aligned}$ button.
::第1步:按Y=按钮。

Step 2: Clear any previous functions (press CLEAR) and turn off any previous plots (arrow up to Plot 1 and press ENTER).
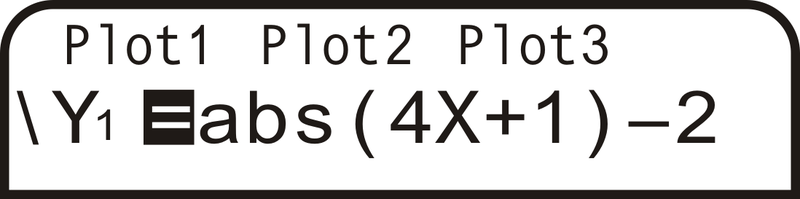
::第2步:清除任何先前的函数(pressCLEAR)并关闭任何先前的绘图(缩到绘图 1 并按 ENTER) 。

Step 3: Press the MATH button, arrow over to NUM and highlight 1:abs (. Press ENTER.
::第3步:按MATH 按钮,向NUM箭头箭头,突出显示1:abs(.按ENTER。)

Step 4: Type in the remaining portion of the function. The screen:
::第4步:在函数的剩余部分输入类型。屏幕 :

Step 5: Press GRAPH. If your screen is off, press ZOOM, scroll down to 6:ZStandard , and press ENTER.
::第5步:按GRAPH键。如果屏幕关闭,按ZOOM键,滚动到 6:ZStandard,按ENTER键。

The graph looks like:
::图表看起来像:

As you can see from the graph, the vertex is not (-1, -2). The $\begin{aligned} y - \end{aligned}$ coordinate is -2, but the 4 inside the absolute value affects the $\begin{aligned} x - \end{aligned}$ coordinate. Set what is inside the absolute value equal to zero to solve for the $\begin{aligned} x - \end{aligned}$ coordinate of the vertex.
::从图中可以看到,顶点不是 (-1, - 2) 。 y - 坐标是 - 2, 但绝对值内4 影响 x - 坐标。设定顶点的 x - 坐标在绝对值内等于零的值, 以解析。

$\begin{aligned} 4 x + 1 & = 0 \\ 4 x & = - 1 \\ x & = - \frac{1}{4} \end{aligned}$

::4x+1=04x @%1x}14

The vertex is $\begin{aligned} (- \frac{1}{4}, - 2) \end{aligned}$ . We know that the domain is all real numbers. The range will be any number greater than and including -2. In this function, the “ $\begin{aligned} a \end{aligned}$ ” term was inside the absolute value. When this happens, it will always affect the $\begin{aligned} x - \end{aligned}$ coordinate of the vertex.
::顶点是 (- 14, - 2) 。我们知道, 域是所有真实的数字。范围会是大于和包含 - 2 的任意数字。在此函数中, “ a” 词在绝对值之内。当发生这种情况时, 它总是会影响顶点的 x - 坐标。

Examples
::实例

Example 1
::例1

Earlier, you were asked to figure out who is right, and to find the vertex of the absolute value function $\begin{aligned} y = - | x + 3 | - 2 \end{aligned}$ .
::早些时候,你被要求找出谁是对的, 并找到绝对值函数 yx+32 的顶点。

Sarai is right. The absolute value function is written in general form, so a calculator is not necessary. The vertex is (–3, –2).
::Sarai是正确的。绝对值函数以一般形式写成, 所以计算器是不必要的。顶点是 ( - 3 ) - 2 。

Example 2
::例2

Graph $\begin{aligned} y = 3 | x + 4 | - 5 \end{aligned}$ without a graphing calculator or making a table. Find the vertex, domain, and range of the function.
::y= 3x+45, 没有图形计算器或绘制表格。查找函数的顶点、域和范围。

First, use the general form to find the vertex, (-4, -5). Then, use $\begin{aligned} a \end{aligned}$ to determine the breadth of the function. $\begin{aligned} a = 3 \end{aligned}$ , so we will move up 3 and over 1 in both directions to find the points on either side of the vertex.
::首先,使用一般格式查找顶点( 4 - 5) , 然后, 使用 a 来确定函数的宽度。 a= 3, 所以我们会在双向上移3 和 1 以上, 在顶点的两侧找到点。

The domain is all real numbers and the range is all reals greater than and including -5.
::域名是所有实际数字,范围都实际大于和包括5。

Domain: $\begin{aligned} x \in R \end{aligned}$
::域: xR

Range: $\begin{aligned} y \in [- 5, \infty) \end{aligned}$
::范围:y[-5,]

Example 3
::例3

Graph $\begin{aligned} y = - 2 | x - 5 | + 1 \end{aligned}$ using a graphing calculator.
::使用图形计算器的 y2x- 51。

Using the steps from the graphing calculator problem above, the function looks like:
::使用以上图形化计算器问题的步骤,该函数看起来像:

Review
::回顾

Graph $\begin{aligned} y = 3 | x | \end{aligned}$ , $\begin{aligned} y = - 3 | x | \end{aligned}$ , and $\begin{aligned} y = | - 3 x | \end{aligned}$ on the same set of axes. Compare the graphs.
::在同一组轴上的 y= 3 x 、 y 3 x 和 y 3x 。比较图表。

Graph $\begin{aligned} y = \frac{1}{4} | x + 1 | \end{aligned}$ , and $\begin{aligned} y = \frac{1}{4} | x | + 1 \end{aligned}$ on the same set of axes. Compare the graphs.
::相同轴组上的 y = 14 x+ 1 和 y = 14 x 1。比较图表。

Without graphing, do you think that $\begin{aligned} y = 2 | x |, y = | 2 x |, \end{aligned}$ and $\begin{aligned} y = | - 2 x | \end{aligned}$ will all produce the same graph? Why or why not?
::没有图形化,你是否认为y=2x,y2x, y2x, 和y2x将产生相同的图表?为什么或为什么不是?

We know that the domain of all absolute value functions is all real numbers. What would be a general rule for the range?
::我们知道,所有绝对值函数的域是所有实际数字。对于范围来说,什么是一般规则?

Use the general form and pattern recognition to graph the following functions. Determine the vertex, domain, and range. No graphing calculators!
::使用一般窗体和图案识别来绘制以下函数的图形。确定顶点、域和范围。不使用图形计算器!

$\begin{aligned} y = | x - 2 | + 5 \end{aligned}$
::yx - 2 @% 5

$\begin{aligned} y = - 2 | x + 3 | \end{aligned}$
::y2x+3

$\begin{aligned} y = \frac{1}{3} | x | + 4 \end{aligned}$
::y=13x4 y=13

$\begin{aligned} y = 2 | x + 1 | - 2 \end{aligned}$
::y=2x+12

$\begin{aligned} y = - \frac{1}{2} | x - 7 | \end{aligned}$
::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

$\begin{aligned} y = - | x - 8 | + 6 \end{aligned}$
::yx - 86

Use a graphing calculator to graph the following functions. Sketch a copy of the graph on your paper. Identify the vertex, domain, and range.
::使用图形计算器来绘制以下函数的图形。在您的纸张上绘制一张图形的副本。标明顶点、域和范围。

$\begin{aligned} y = - 4 | 2 x + 1 | \end{aligned}$
::~ ~ ~ ~ 2x+1 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

$\begin{aligned} y = \frac{2}{3} | x - 4 | + \frac{1}{2} \end{aligned}$
::y=23x -4*12

$\begin{aligned} y = \frac{4}{3} | 2 x - 3 | - \frac{7}{2} \end{aligned}$
::y=432x-372

Graphing Calculator Extension Use the graphing calculator to answer questions 14-16.
::图形计算扩展使用图形计算器回答问题14-16。

Graph $\begin{aligned} y = x^{2} - 4 \end{aligned}$ on your calculator. Sketch the graph and determine the domain and range.
::计算器上的 y=x2-4 图形。绘制图形并确定域和范围。

Graph $\begin{aligned} y = | x^{2} - 4 | \end{aligned}$ on your calculator. Sketch graph and determine the domain and range.
::计算器上的 yx2- 4 图形。折叠图, 确定域和范围。

How do the two graphs compare? How are they different? What could you do to the first graph to get the second?
::这两个图是如何比较的?它们有什么不同?你能对第一个图做什么才能拿到第二个图呢?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

使用普通绝对值平方和图形计算器

General Form of an Absolute Value Function ::绝对值函数的一般形式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)

General Form of an Absolute Value Function
::绝对值函数的一般形式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Review
::回顾

Review (Answers)
::回顾(答复)