Course: 3.3 使用图形化的溶解系统无任何或无限多的溶解方法

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 使用图形化的无或无限多解决方案的溶解系统

Collapse Expand
使用图形化的无或无限多解决方案的溶解系统
At a craft fair, Jamal bought two wooden crafts and one needlework craft for a total of $21. At the same craft fair, Kenia bought two needlework crafts and four wooden crafts for a total of $28. Did Jamal and Kenia buy the same items? Why or why not? Assume no discounts were offered.
::在一次工艺博览会上,Jamal购买了两件木制工艺品和一件针头工艺品,共计21美元;在同一工艺博览会上,Kenia购买了两件针头工艺品和四件木制工艺品,共计28美元;Jamal和Kenia买的物品相同吗?为什么没有?假设没有提供折扣。

Systems with No or Infinitely Many Solutions Using Graphing
::使用图形化的系统没有或无限多的解决方案

So far we have looked at linear systems of equations in which the lines always intersected in one, unique point. What happens if this is not the case? What could the graph of the two lines look like?
::到目前为止,我们一直在研究线性方程体系,其中线性方程总是在一个独特的点上交叉。如果情况并非如此,会发生什么情况?两条线的图像是什么?

Let's graph the following systems.
::让我们用图表显示以下系统。

$\begin{aligned} y & = 2 x - 5 \\ y & = 2 x + 4 \end{aligned}$
$\begin{align*}y &= 2x-5\\ y &= 2x+4\end{align*}$
::y=2x-5y=2x+4 y=2x-5y=2x+4

In this problem both lines have the same but different $\begin{align*}y-\end{align*}$ intercepts . When graphed, they are parallel lines and never intersect. This system has no solution. Another way to say this is to say that it is inconsistent .
::在此问题上,两条线都有相同但不同的y- interinter 。图表显示时, 它们是平行线, 从未交叉。这个系统没有解决方案。另一种说法是说它不一致。

$\begin{aligned} 2 x - 3 y & = 6 \\ - 4 x + 6 y & = - 12 \end{aligned}$
$\begin{align*}2x-3y &= 6\\ -4x + 6y &= -12\end{align*}$
::2 - 3y=6-4x+6y12

In this problem both lines have the same slope and $\begin{align*}y-\end{align*}$ intercept . This is more apparent when the equations are written in slope intercept form :
::在这个问题上,两条线的斜坡和y-intercide是相同的。当方程式以斜坡截击形式写成时,这一点就更加明显:

$\begin{aligned} y = \frac{2}{3} x - 2 a n d y = \frac{2}{3} x - 2 \end{aligned}$
$\begin{align*} y = \frac{2}{3}x-2 \ and \ y = \frac{2}{3}x-2\end{align*}$
::y=23x-2和y=23x-2

When we graph them, they are one line, coincident , meaning they have all points in common. This means that there are an infinite number of solutions to the system. Because this system has at least one solution it is considered to be consistent .
::当我们绘制它们时,它们是一个线条,重复,意思是它们有所有点的共同点。这意味着系统有无限数量的解决方案。由于这个系统至少有一个解决方案,它被认为是一致的。

Consistent systems are systems which have at least one solution. If the system has exactly one, unique solution then it is independent . If the system has infinite solutions, then it is called dependent .
::一致的系统是至少有一个解决方案的系统。如果系统有一个独特的解决方案,那么它是独立的。如果系统有无限的解决方案,那么它就被称为依赖。

Let's classify the following system:
::让我们对以下系统进行分类:

$\begin{aligned} 10 x - 2 y & = 10 \\ y & = 5 x - 5 \end{aligned}$
$\begin{align*}10x-2y &= 10\\ y &= 5x-5\end{align*}$
::10--2y=10y=5x-5

Rearranging the first equation into slope intercept form we get $\begin{align*}y=5x-5\end{align*}$ , which is exactly the same as the second equation. This means that they are the same line. Therefore the system is consistent and dependent.
::将第一个方程式重新排列为斜坡拦截表,我们得到的y=5x-5与第二个方程式完全相同。这意味着它们是相同的线条。因此,系统是一致和依赖的。

Examples
::实例

Example 1
::例1

Earlier, you were asked if Jamal and Kenia bought the same items.
::早些时候,有人问你Jamal和Kenia是否购买了同样的物品。

The system of linear equations represented by this situation is:
$\begin{aligned} 2 w + n & = 21 \\ 4 w + 2 n & = 28 \end{aligned}$
$\begin{align*}2w + n &= 21\\ 4w + 2n &= 28\end{align*}$
::以这种情形表示的线性方程式系统为: 2w+n=214w+2n=28

If you graph these two linear equations on the same graph, there is no point of intersection . Therefore there is no solution and Jamal and Kenia couldn't have bought the same items.
::如果您在同一图表上用图形显示这两个线性方程, 就不会有交叉点。因此没有解决方案, Jamal 和 Kenia 无法购买相同的物品。

Classify the following systems as consistent, inconsistent, independent or dependent. You may do this with or without graphing them. You do not need to find the unique solution if there is one.
::将以下系统分类为一致、不一致、独立或依赖性。您可以使用或不绘制图表的方式这样做。如果存在,您不需要找到唯一的解决方案。

Example 2

$\begin{aligned} 5 x - y & = 15 \\ x + 5 y & = 15 \end{aligned}$
$\begin{align*}5x-y &= 15\\ x+5y &= 15\end{align*}$
::例2 5x-y=15x+5y=15

The first step is to rearrange both equations into slope intercept form so that we can compare these attributes.
::第一步是将两个方程式重新排列为斜坡拦截形式,以便我们可以比较这些属性。

$\begin{aligned} 5 x - y & = 15 \to y = 5 x - 15 \\ x + 5 y & = 15 \to y = - \frac{1}{5} x + 3 \end{aligned}$
$\begin{align*}5x-y &= 15 \rightarrow y=5x-15\\ x+5y &= 15 \rightarrow y= - \frac{1}{5}x+3\end{align*}$
::5-y=15-y=5x-15x+5y=15-y=15-y=15x+3

The slopes are not the same so the lines are neither parallel nor coincident. Therefore, the lines must intersect in one point. The system is consistent and independent.
::斜坡不同, 所以线条既不平行也不巧合。因此, 线条必须在一个点上交叉。系统是一致和独立的。

Example 3

$\begin{aligned} 9 x - 12 y & = - 24 \\ - 3 x + 4 y & = 8 \end{aligned}$
$\begin{align*}9x-12y &= -24\\ -3x+4y &= 8\end{align*}$
::例3 9x-12y24-3x+4y=8

Again, rearrange the equations into slope intercept form:
::再次将方程式重新排列为斜坡拦截形式:

$\begin{aligned} 9 x - 12 y = - 24 & \to y = \frac{3}{4} x + 2 \\ - 3 x + 4 y = 8 & \to y = \frac{3}{4} x + 2 \end{aligned}$
$\begin{align*}9x-12y = -24 & \rightarrow y=\frac{3}{4}x+2 \\ -3x+4y = 8 & \rightarrow y=\frac{3}{4}x+2 \end{align*}$
::9 - 12y24y=34x+2 - 3x+4y=8y=34x+2

Now, we can see that both the slope and the $\begin{align*}y-\end{align*}$ intercept are the same and therefore the lines are coincident. The system is consistent and dependent.
::现在,我们可以看到,斜坡和y - interview 都是一样的, 因此线条是同时的。系统是一贯的, 并依附的。

Example 4

$\begin{aligned} 6 x + 8 y & = 12 \\ - 3 x - 4 y & = 10 \end{aligned}$
$\begin{align*}6x+8y &= 12\\ -3x-4y &= 10\end{align*}$
::示例4 6x+8y=12-3x-4y=10

The equations can be rewritten as follows:
::这些方程式可改写如下:

$\begin{aligned} 6 x + 8 y & = 12 \to y = - \frac{3}{4} x + \frac{3}{2} \\ - 3 x - 4 y & = 10 \to y = - \frac{3}{4} x - \frac{5}{2} \end{aligned}$
$\begin{align*}6x+8y &= 12 \rightarrow y= - \frac{3}{4}x+\frac{3}{2} \\ -3x-4y &= 10 \rightarrow y= - \frac{3}{4}x-\frac{5}{2} \end{align*}$
::6x+8y=12y34x+32-33x-4y=10y34x-52

In this system the lines have the same slope but different $\begin{align*}y-\end{align*}$ intercepts so they are parallel lines. Therefore the system is inconsistent. There is no solution.
::在这个系统中,线条有相同的斜坡,但有不同的y-inter概念,因此它们是平行的线条。因此,这个系统是不一致的。没有解决办法。

Review
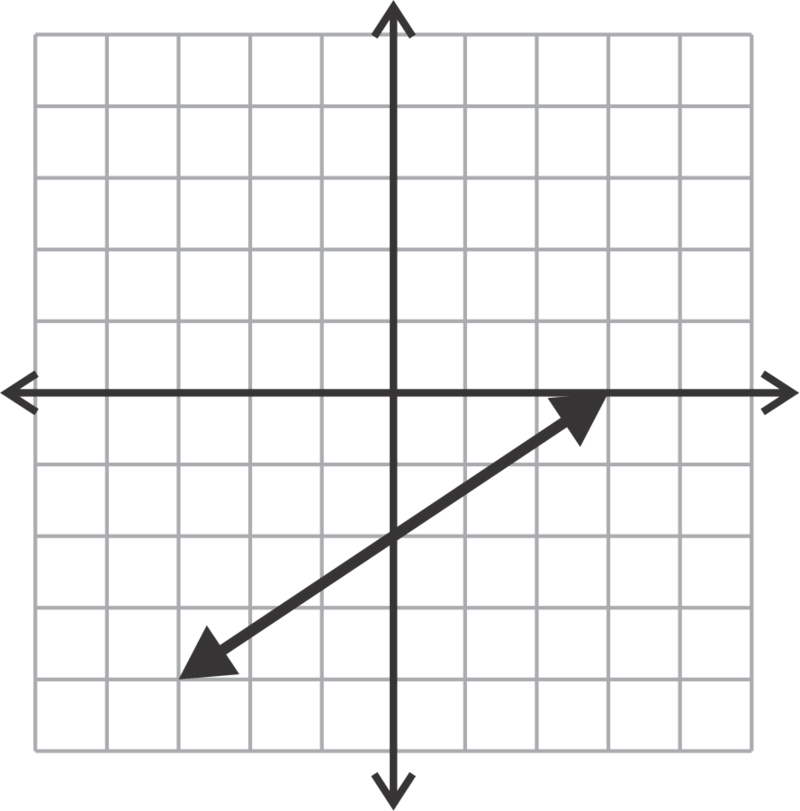
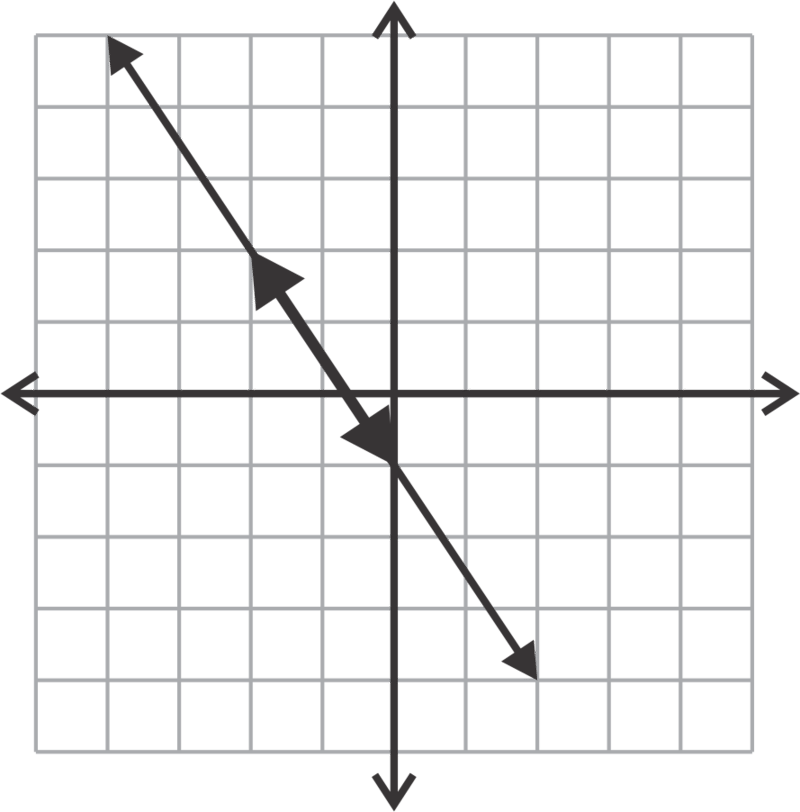
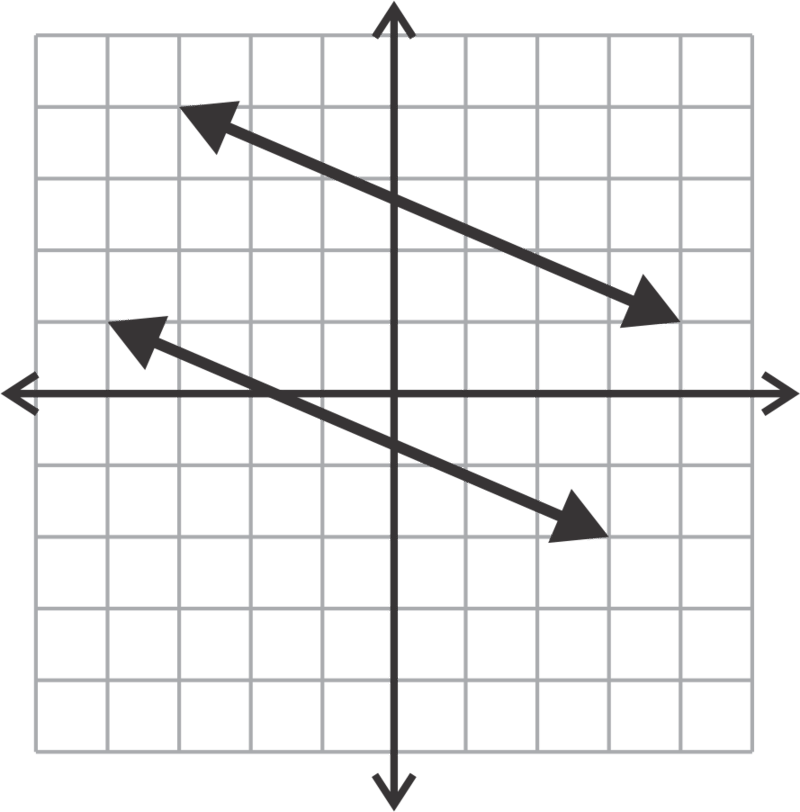
::回顾

Describe the systems graphed below both algebraically (consistent, inconsistent, dependent, independent) and geometrically (intersecting lines, parallel lines, coincident lines).
::描述在代数(一致、不一致、依赖、独立)和几何(交叉线、平行线、正对线)下图解的系统。

Classify the following systems as consistent, inconsistent, independent or dependent. You may do this with or without graphing them. You do not need to find the unique solution if there is one.
::将以下系统分类为一致、不一致、独立或依赖性。您可以使用或不绘制图表的方式这样做。如果存在,您不需要找到唯一的解决方案。

.

$\begin{aligned} 4 x - y & = 8 \\ y & = 4 x + 3 \end{aligned}$
$\begin{align*}4x-y &= 8\\ y &= 4x+3\end{align*}$

.

$\begin{aligned} 5 x + y & = 10 \\ y & = 5 x + 10 \end{aligned}$
$\begin{align*}5x+y &= 10\\ y &= 5x+10\end{align*}$

.

$\begin{aligned} 2 x - 2 y & = 11 \\ y & = x + 13 \end{aligned}$
$\begin{align*}2x-2y &= 11\\ y &= x+13\end{align*}$

.

$\begin{aligned} - 7 x + 3 y & = - 21 \\ 14 x - 6 y & = 42 \end{aligned}$
$\begin{align*}-7x+3y &= -21\\ 14x-6y &= 42\end{align*}$

.

$\begin{aligned} y & = - \frac{3}{5} x + 1 \\ 3 x + 5 y & = 5 \end{aligned}$
$\begin{align*}y &= - \frac{3}{5}x+1\\ 3x+5y &= 5\end{align*}$

.

$\begin{aligned} 6 x - y & = 18 \\ y & = \frac{1}{6} x + 3 \end{aligned}$
$\begin{align*}6x-y &= 18\\ y &= \frac{1}{6}x+3\end{align*}$

In problems 10-15 you will be writing your own systems. Your equations should be in standard form, $\begin{align*}Ax+By=C\end{align*}$ . Try to make them look different even if they are the same equation.
::在问题 10 - 15 中, 您将写入您自己的系统。您的方程式应该以标准格式 Ax+By=C 表示。试着让它们看起来不同, 即使它们是相同的方程式。

Write a system which is consistent and independent.
::写一个前后一致和独立的系统。

Write a system which is consistent and dependent.
::写一个前后一致和依赖性的系统。

Write a system which is inconsistent.
::写一个不一致的系统。

Write a system where the solution is (-1, 2), one line is vertical and the second is horizontal.
::写入一个系统, 其解决方案是 (-1, 2) , 一条线是垂直的, 第二条是水平的。

Write a system where the solution is (-1, 2), one line is vertical or horizontal and the second is neither.
::写入一个系统, 其解决方案是 (-1, 2) , 一条线是垂直的或水平的, 而第二条既不是垂直的, 也不是横向的。

Write a system where the solution is (-1, 2) and neither line is vertical nor horizontal.
::写入解决方案所在的系统( 1, 2) , 既不是垂直线, 也不是水平线。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

3.3 使用图形化的溶解系统无任何或无限多的溶解方法

Section outline

General

使用图形化的无或无限多解决方案的溶解系统

Systems with No or Infinitely Many Solutions Using Graphing
::使用图形化的系统没有或无限多的解决方案

Examples
::实例

Example 1
::例1

Example 2

$\begin{aligned} 5 x - y & = 15 \\ x + 5 y & = 15 \end{aligned}$
$\begin{align}5x-y &= 15\\ x+5y &= 15\end{align}$
::例2 5x-y=15x+5y=15

Example 3

$\begin{aligned} 9 x - 12 y & = - 24 \\ - 3 x + 4 y & = 8 \end{aligned}$
$\begin{align}9x-12y &= -24\\ -3x+4y &= 8\end{align}$
::例3 9x-12y24-3x+4y=8

Example 4

$\begin{aligned} 6 x + 8 y & = 12 \\ - 3 x - 4 y & = 10 \end{aligned}$
$\begin{align}6x+8y &= 12\\ -3x-4y &= 10\end{align}$
::示例4 6x+8y=12-3x-4y=10

Review
::回顾

Review (Answers)
::回顾(答复)

Section outline

General

使用图形化的无或无限多解决方案的溶解系统

Systems with No or Infinitely Many Solutions Using Graphing ::使用图形化的系统没有或无限多的解决方案

Examples ::实例

Example 1 ::例1

Example 2 5 x − y = 15 x + 5 y = 15 \begin{align*}5x-y &= 15\\ x+5y &= 15\end{align*} ::例2 5x-y=15x+5y=15

Example 3 9 x − 12 y = − 24 − 3 x + 4 y = 8 \begin{align*}9x-12y &= -24\\ -3x+4y &= 8\end{align*} ::例3 9x-12y24-3x+4y=8

Example 4 6 x + 8 y = 12 − 3 x − 4 y = 10 \begin{align*}6x+8y &= 12\\ -3x-4y &= 10\end{align*} ::示例4 6x+8y=12-3x-4y=10

Review ::回顾

Review (Answers) ::回顾(答复)

Systems with No or Infinitely Many Solutions Using Graphing
::使用图形化的系统没有或无限多的解决方案

Examples
::实例

Example 1
::例1

Example 2

$\begin{aligned} 5 x - y & = 15 \\ x + 5 y & = 15 \end{aligned}$
$\begin{align}5x-y &= 15\\ x+5y &= 15\end{align}$
::例2 5x-y=15x+5y=15

Example 3

$\begin{aligned} 9 x - 12 y & = - 24 \\ - 3 x + 4 y & = 8 \end{aligned}$
$\begin{align}9x-12y &= -24\\ -3x+4y &= 8\end{align}$
::例3 9x-12y24-3x+4y=8

Example 4

$\begin{aligned} 6 x + 8 y & = 12 \\ - 3 x - 4 y & = 10 \end{aligned}$
$\begin{align}6x+8y &= 12\\ -3x-4y &= 10\end{align}$
::示例4 6x+8y=12-3x-4y=10

Review
::回顾

Review (Answers)
::回顾(答复)