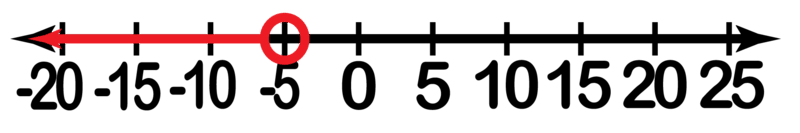课程： 1.3 区间和区间表示法

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

区间和区间表示法

Suppose you and 2 of your friends were out for lunch and decide to buy tacos. Together you have $15 to spend on lunch, and tacos are $1.25 each. It is clear that the total cost could be graphed as a function of the number of tacos purchased, but how would you specify that the graph should not include values greater than $15 or less than $3.75 (one taco each)?
::假设你和两个朋友出去吃午饭,决定买玉米饼。你们一起有15美元午餐,玉米饼每人1.25美元。很明显,总成本可以用购买玉米饼数量的函数来计算,但您如何具体说明图表中数值不应超过15美元或小于3.75美元(每张玉米饼)?

Intervals and Interval Notation
::区间和区间表示法

Real Values and Intervals
::实际价值和间数

A function is defined as a real function if both the domain and the range are sets of real numbers. Many of the functions you have likely encountered before are real functions, and many of these functions have Domain = $\begin{aligned} R \end{aligned}$ . Consider, for example, the function $\begin{aligned} y = 3 x \end{aligned}$ . A section of the graph of this function is shown below.
::如果域和范围都是实际数字的组合,函数就被定义为实际函数。您以前可能遇到的许多函数都是实际函数,而其中许多函数是域 = R。例如,请考虑函数 y=3x。此函数图中的一节如下所示。

You may already be familiar with the graphs of lines. In particular, you may already be in the habit of placing arrows at the ends. We do this in order to indicate that the line will continue forever in both the positive and negative directions, both in terms of the domain and the range. The line above, however, only shows the function $\begin{aligned} y = 3 x \end{aligned}$ on the interval [-3, 3]. The square brackets indicate that the graph includes the endpoints of the interval, where x = -3 and x = 3. We call this a closed interval . A closed interval contains its endpoints. In contrast, an open interval does not contain its endpoints. We indicate an open interval with " data-term="Parentheses"> parentheses . For example, (-3, 3) indicates the set of numbers between -3 and 3, not including -3 and 3. You may have noticed that the open interval notation looks like the notation for a point ( x, y ) in the plane. It is important to read an example or a homework problem carefully to avoid confusing a point with an interval! The difference is generally quite clear from the context.
::您可能已经熟悉行的图表。特别是, 您可能已经习惯在结尾处放置箭头。我们这样做是为了表明线条将永远在正向和负向上继续, 包括域和范围。但是, 上面的线条只显示间距[ 3, 3] 上的 y=3x 函数。方括号表示, 图形包括间距的端点, 其中 x = - 3 和 x = 3 = 3 。我们称此为封闭间隔。一个封闭间隔包含它的端点。相反, 一个开放间隔不包含它的端点。我们用括号表示一个开放间隔。例如, (3, 3 3) 表示数字在 - 3 3 和 3 和 3 之间的一组。您可能注意到, 开间距的标记看上去像在平面上一个点( x, y) 的标记。重要的是要仔细阅读一个示例或一个功课问题, 以避免将点与间距混淆。。差异通常从上非常清楚。

The table below summarizes the kinds of intervals you may need to consider while studying functions and their domains:
::下表概述了您在研究函数及其领域时可能需要考虑的间隔类型:

Interval notation	Inequality notation	Description
$\begin{aligned} [a, b] \end{aligned}$	$\begin{aligned} a \leq x \leq b \end{aligned}$	The value of x is between a and b , including a and b , where a , b are real numbers.
$\begin{aligned} (a, b) \end{aligned}$	$\begin{aligned} a < x < b \end{aligned}$	The value of x is between a and b , not including a and b .
$\begin{aligned} [a, b) \end{aligned}$	$\begin{aligned} a \leq x < b \end{aligned}$	The value of x is between a and b , including a, but not including b .
$\begin{aligned} (a, b] \end{aligned}$	$\begin{aligned} a < x \leq b \end{aligned}$	The value of x is between a and b , including b , but not including a .
$\begin{aligned} (a, \infty) \end{aligned}$	$\begin{aligned} x > a \end{aligned}$	The value of x is strictly greater than a .
$\begin{aligned} [a, \infty) \end{aligned}$	$\begin{aligned} x \geq a \end{aligned}$	The value of x is greater than or equal to a
$\begin{aligned} (- \infty, a) \end{aligned}$	$\begin{aligned} x < a \end{aligned}$	The value of x is strictly less than a
$\begin{aligned} (- \infty, a] \end{aligned}$	$\begin{aligned} x \leq a \end{aligned}$	The value of x is less than or equal to a .

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about buying tacos for lunch.
::早些时候,有人给了你一个问题买玉米饼当午餐。

Together, you have $15 to spend on lunch, and tacos are $1.25 each. It is clear that the total cost could be graphed as a function of the number of tacos purchased, but how would you specify that the graph should not include values greater than $15 or less than $3.75 (one taco each)?
::共需15美元午餐,而玉米卷每份为1.25美元。成本总额显然可以按购买玉米卷的数量来计算,但您如何具体说明图表中数值不应大于15美元或小于3.75美元(每张玉米卷)?

To specify that the graph of the cost of lunch only includes values between $3.75 and $15.00, specify the interval of the domain as: [3.75, 15].
::要具体说明午餐成本图只包括3.75至15.00之间的值,请注明域间距为:[3.75、15]。

Example 2
::例2

Identify the sets described:
::查明所述各套资料:

$\begin{aligned} (- 3, 9] \end{aligned}$

The set of numbers between -3 and 9, ‘‘not including’’ the actual value of -3, but ‘‘including’’ 9.
::数字组在 -3和9之间,不包括实际值 -3,但包括_9。

$\begin{aligned} [- 23, 12] \end{aligned}$

The set of numbers between -23 and 12, ‘‘including’’ the values -23 and 12.
::在 -23 和 12 之间的数组, 包括值 - 23 和 12 。

$\begin{aligned} (- \infty, 0) \end{aligned}$

All numbers less than 0, not including 0 itself.
::所有数字小于 0, 不包括 0 本身。

Example 3
::例3

Sketch the graph of the function $\begin{aligned} f (x) = \frac{1}{2} x - 6 \end{aligned}$ on the interval [-4, 12).
::在间隔[4, 12] 上绘制函数 f(x)=12x- 6的图示 [, 12] 。

The figure below shows a graph of $\begin{aligned} f (x) = \frac{1}{2} x - 6 \end{aligned}$ on the given interval:
::下图显示给定间隔的 f( x) = 12x- 6 的图形 :

Example 4
::例4

Describe the specified intervals, use interval notation:
::描述指定的间隔, 使用间隔符号 :

All positive numbers
::所有正数

$\begin{aligned} (0, + \infty) \end{aligned}$

Zero is neither positive nor negative, so the “(“ is used to specify that zero is ‘‘not’’ included. Since there is no maximum positive number, we specify that infinity is the upper value, and use “)” since it cannot be reached.
::零既不是正数,也不是负数,因此““”用于具体说明零是包括在内的。由于没有最大正数,我们规定无限值是上限,使用“)”因为无法达到。

The numbers between negative eight and two hundred forty two, including both.
::数字介于负八至二百四十二之间,包括两者。

$\begin{aligned} [- 8, 242] \end{aligned}$

The “[“ is used on both ends, since both values are included.
::“[“用于两个目的,因为两个数值都包括在内。

All negative numbers, zero, and the positive numbers up to and including nine.
::所有负数,0,正数,直到9岁,包括9岁。

$\begin{aligned} (- \infty, 9] \end{aligned}$

The “(“ denotes that negative infinity cannot be reached, and “]” on the other end specifies that 9 is included in the set.
::“ " 表示无法达到负无限, " 在另一端 " , " ] " 规定将9列入这套办法。

Example 5
::例5

Describe the domain and range in the sets in the images below using interval notation.
::使用间距符号描述下方图像集中的域和范围。

a.		b.

The domain is the set of x values starting with the included -6 and ending at 4 , which is not included: [-6, 4).
::域名是一组 x 值,从包含 -6 开始,至 4 结束,但不包括 [6, 4 。

The range is the set of y values from -3 (not included) to 4 (included): (-3, 4].
::范围为Y值组,从-3(不包括)至4(包括)-3,4)不等。

Domain: [-6, 7) (from above)
::域:[6、7](以上)

Range : [-1, 6) (from above)
::范围:[-1,6](以上)

Review
::回顾

Write the following in interval notation.
::在间距符号中写下以下文字。

$\begin{aligned} - 3 \leq x < 1 \end{aligned}$
::- 3x<1

$\begin{aligned} 0 < x < 2 \end{aligned}$
::0 <x <2

$\begin{aligned} x > - 3 \end{aligned}$
::x% 3

$\begin{aligned} x \leq 2 \end{aligned}$
::x% 2

Solve and put your answer in interval notation.
::解答并用间距标注你的答案

$\begin{aligned} - 2 x + 3 < 1 \end{aligned}$
::-2x+3 < 1

$\begin{aligned} 7 x + 4 \leq 2 x - 6 \end{aligned}$
::7x+42x-6

For each number line, write the given set of numbers in interval notation.
::对于每一数字行,请在间距符号中填写给定的一组数字。

Name the domain and range for each relation using interval notation.
::使用间距符号为每个关系指定域和范围。

Express the following sets using interval notation, then sketch them on a number line.
::使用间距符号表示以下各组表示,然后用数字线将其绘制成草图。

{ $\begin{aligned} x : - 1 \leq x \leq 3 \end{aligned}$ }
::x: -1x3}

{ $\begin{aligned} x : - 2 \leq x < 1 \end{aligned}$ }
::{x:-2x<1}

A is the set of all numbers bigger than 2 but less than or equal to 5.
::A 是指所有数字的一组,数字大于2但小于或等于5。

{ $\begin{aligned} x : - 3 < x < \infty \end{aligned}$ }
::{x: -3 <x} {x: -3 <x}

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

区间和区间表示法

Intervals and Interval Notation ::区间和区间表示法

Real Values and Intervals ::实际价值和间数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)