课程： 5.15 寻找帕拉波拉部分

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节查找帕拉波拉的部分

折叠展开
查找帕拉波拉的部分
The profit on your school fundraiser is represented by the quadratic expression $\begin{align*}-3p^2 + 200p - 3000\end{align*}$ , where p is your price point. What price point will result in the maximum profit and what is that maximum profit? Hint: Find the vertex of the parabola .
::学校募款人的利润由四边表达式- 3p2+200p- 3000表示, p是您的价格点。什么价格点能带来最大利润,什么能带来最大利润? 提示: 找到抛物线的顶端。

Parts of a Parabola
::帕拉波拉部分

Now that we have found the solutions of a quadratic equation we will graph the function . First, we need to introduce $\begin{align*}y\end{align*}$ or $\begin{align*}f(x)\end{align*}$ . A quadratic function is written $\begin{align*}y=ax^2+bx+c\end{align*}$ or $\begin{align*}f(x)=ax^2+bx+c\end{align*}$ . All quadratic equations are also functions.
::现在我们找到了四方方程式的解决方案, 我们将绘制函数图。首先, 我们需要引入 y 或 f( x) 。一个二次函数是写成的 y= ax2+bx+c 或 f( x) = ax2+bx+c 。所有二次方程式也是函数。

Recall that the solutions of a quadratic equation are found when the equation is set equal to zero. This is also the same as when $\begin{align*}y = 0\end{align*}$ . Therefore , the solutions of a quadratic equation are also the $\begin{align*}{\color{red}x-\mathbf{intercepts}}\end{align*}$ of that function, when graphed.
::回顾当方程式设定为零时,会发现二次方程式的解决方案。这也与y=0时相同。因此,二次方程式的解决方案也是该函数的 x- intercuts, 当绘制图表时。

The graph of a quadratic equation is called a $\begin{align*}{\color{blue}\mathbf{parabola}}\end{align*}$ and looks like the figure to the left. A parabola always has “U” shape and depending on certain values, can be wider or narrower. The lowest part of a parabola, or minimum, is called the $\begin{align*}{\color{green}\mathbf{vertex}}\end{align*}$ . Parabolas can also be flipped upside-down, and in this case, the vertex would be the maximum value. Notice that this parabola is symmetrical about vertical line that passes through the vertex. This line is called the axis of . Lastly, where the parabola passes through the $\begin{align*}y-\end{align*}$ axis (when $\begin{align*}x = 0\end{align*}$ ), is the $\begin{align*}{\color{magenta}y-\mathbf{intercept}}\end{align*}$ .
::二次方程的图形称为抛物线,看起来像左边的图。抛物线的形状总是“ U”形,取决于某些值,可以扩大或缩小。抛物线的最低部分, 或最小部分, 称为顶点。 Parabolas 也可以向上翻转, 而在此情况下, 顶点将是最大值。请注意, 此抛物线与垂直线对称, 垂直线穿过顶点。此直线被称为。最后, 抛物线穿过 y- 轴( 当 x=0 时) , 是 y- inter 。

If you are given (or can find) the $\begin{align*}x-\end{align*}$ intercepts and the vertex, you can always graph a parabola.
::如果给定(或可以找到) x - 界面和顶点,您总是可以绘制抛物线图。

Finding the Vertex of a Parabola
::找到帕拉波拉的顶点

Step 1: The equation of the parabola above is $\begin{align*}y=x^2-2x-3\end{align*}$ . Find $\begin{align*}a, b,\end{align*}$ and $\begin{align*}c\end{align*}$ . $\begin{align*}a=1,b=-2,c=-3\end{align*}$
::第1步:以上抛物线的方程式是y=x2-2x-3。查找 a、b 和 c. a= 1, b =2, c =3

Step 2: What are the coordinates of the vertex? (1, -4)
::第2步:顶端的坐标是什么? (1, 4)

Step 3: Create an expression using $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ (from Step 1) that would be equal to the $\begin{align*}x-\end{align*}$ coordinate of the vertex. $\begin{align*}1=\frac{-b}{2a}\end{align*}$
::第3步:用 a 和 b (从第1步开始) 创建一个表达式,该表达式将等于顶端的 x - 坐标。

Step 4: Plug in $\begin{align*}x = 1\end{align*}$ to the equation of the parabola. What do you get for $\begin{align*}y\end{align*}$ ? $\begin{align*}y = -4\end{align*}$
::步骤 4 : 在 parbola 的方程中插入 x=1 中的插件。您能得到什么 y? y = 4

W e have now introduced how to find the vertex of a parabola . The $\begin{align*}x-\end{align*}$ coordinate of the vertex is $\begin{align*}x=\frac{-b}{2a}\end{align*}$ . To find $\begin{align*}y\end{align*}$ , plug in this value to the equation, also written $\begin{align*}f\left(\frac{-b}{2a}\right)\end{align*}$ . $\begin{align*}x=\frac{-b}{2a}\end{align*}$ is also the equation of the axis of symmetry.
::我们现在引入了如何找到抛物线的顶点。顶点的 x - 坐标是 x b2a。要找到 y, 将这个值插入方程, 还要写入 f (- b2a) 。 x b2a 也是对称轴的方程。

Let's find the vertex, axis of symmetry, $\begin{align*}x-\end{align*}$ intercepts, and $\begin{align*}y-\end{align*}$ intercept of $\begin{align*}y=-\frac{1}{2}x^2-2x+6\end{align*}$ .
::让我们找到顶部、对称轴、 X - 界面和y - interview y12x2 - 2x+6 的顶部、轴轴。

First, let’s find the $\begin{align*}x-\end{align*}$ intercepts. This equation is factorable and $\begin{align*}ac = -3\end{align*}$ . The factors of -3 that add up to -2 are -3 and 1. Expand the $\begin{align*}x-\end{align*}$ term and factor .
::首先,让我们找到 x- intercuts。这个方程式是可因数和 ac\%3. 3 乘以 - 2 的 - 3 系数是 - 3 和 1. 扩大 x- 期数和因数。

$\begin{aligned} - \frac{1}{2} x^{2} - 2 x + 6 & = 0 \\ - \frac{1}{2} x^{2} - 3 x + x + 6 & = 0 \\ - x (\frac{1}{2} x + 3) + 2 (\frac{1}{2} x + 3) & = 0 \\ (\frac{1}{2} x + 3) (- x + 2) & = 0 \end{aligned}$
$\begin{align*}-\frac{1}{2}x^2-2x+6 &=0\\ -\frac{1}{2}x^2-3x+x+6 &=0\\ -x\left(\frac{1}{2}x+3\right)+2\left(\frac{1}{2}x+3\right) &=0\\ \left(\frac{1}{2}x+3\right)(-x+2) &=0\end{align*}$
::-12x2-2x+6=0-12x2-3x+6=0xx(12x+3)+2(12x+3)+2(12x+3)=0(12x+3)(-x+2)=0

Solving for $\begin{align*}x\end{align*}$ , the intercepts are (-6, 0) and (2, 0).
::x的解答是(-6,0)和(2,0)。

To find the vertex, use $\begin{align*}x=\frac{-b}{2a}\end{align*}$ .
::要找到顶点, 请使用 xb2a 。

$\begin{align*}x=\frac{-(-2)}{2 \cdot -\frac{1}{2}}=\frac{2}{-1}=-2\end{align*}$ Plug this into the equation: $\begin{align*}y=-\frac{1}{2}(-2)^2-2(-2)+6=-2+4+6=8\end{align*}$ .
::x(-2)2,212=2-12 将它插入方程:y12(-2)2-2-2(-2)-2,+62+4+6=8。

Therefore, the vertex is (-2, 8) and the axis of symmetry is $\begin{align*}x = -2\end{align*}$ .
::因此,顶部是 (-2, 8) ,对称轴是 x2 。

To find the $\begin{align*}y-\end{align*}$ intercept, $\begin{align*}x = 0\end{align*}$ . $\begin{align*}y=-\frac{1}{2}(0)^2-2(0)+6=6\end{align*}$ . Therefore, the $\begin{align*}y-\end{align*}$ intercept is (0, 6).
::要找到 y - 界面, x=0. y12(0)2- 2(0)+6=6. 因此, y - 界面是 (0, 6) 。

Now, let's sketch a graph of the parabola from the previous problem.
::现在,让我们勾画一下上一个问题的抛物线图。

Plot the vertex and two $\begin{align*}x-\end{align*}$ intercepts (red points). Plot the $\begin{align*}y-\end{align*}$ intercept. Because all parabolas are symmetric, the corresponding point on the other side would be (-4, 6). Connect the five points to form the parabola.
::绘制顶点和两个 X - 截面( 红点) 。绘制 y - 截面。由于所有 parabolas 都是对称的, 另一侧的相应点将是 ( 4 、 6 ) 。连接 5 个点组成 parbola 。

For this parabola, the vertex is the maximum value. If you look at the equation, $\begin{align*}y=-\frac{1}{2}x^2-2x+6\end{align*}$ , we see that the $\begin{align*}a\end{align*}$ value is negative. When $\begin{align*}a\end{align*}$ is negative, the sides of the parabola, will point down.
::对于此抛物线, 顶点是最大值。如果您查看公式 y 12x2-2x+6, 我们可以看到一个值为负值。当一个值为负值时, 抛物线的侧面会点下。

Finally, let's find the vertex and $\begin{align*}x-\end{align*}$ intercepts of $\begin{align*}y=2x^2-5x-25\end{align*}$ . Then, sketch the graph.
::最后,让我们找到 y= 2x2 - 5x- 25 的顶端和 x - 截取点。然后绘制图表。

First, this is a factorable function. $\begin{align*}ac = -50\end{align*}$ . The factors of -50 that add up to -5 are -10 and 5.
::首先,这是一个可因数函数。 ac50。 -50的系数加到 -5是 -10 和 5。

$\begin{aligned} 2 x^{2} - 5 x - 25 & = 0 \\ 2 x^{2} - 10 x + 5 x - 25 & = 0 \\ 2 x (x - 5) + 5 (x - 5) & = 0 \\ (2 x + 5) (x - 5) & = 0 \end{aligned}$
$\begin{align*}2x^2-5x-25 &=0\\ 2x^2-10x+5x-25 &=0\\ 2x(x-5)+5(x-5) &=0\\ (2x+5)(x-5) &=0\end{align*}$
::2x2-5x-25=02x2-10x+5x-25x=02x(x-5)+5(x-5)=0(2x+5)(x-5)=0

Setting each factor equal to zero, we get $\begin{align*}x = 5\end{align*}$ and $\begin{align*}-\frac{5}{2}\end{align*}$ .
::设定每个系数等于零, 我们得到x=5和-52。

From this, we get that the $\begin{align*}x-\end{align*}$ intercepts are (5, 0) and $\begin{align*}\left(-\frac{5}{2},0\right)\end{align*}$ . To find the vertex, use $\begin{align*}x=\frac{-b}{2a}\end{align*}$ .
::我们从这里得知 X - 界面是 (5, 0) 和 (-52, 0) 。要找到顶端, 请使用 x b2a 。

$\begin{align*}x = \frac{5}{2 \cdot 2}=\frac{5}{4}\end{align*}$ Now, find $\begin{align*}y\end{align*}$ . $\begin{align*}y=2\left(\frac{5}{4}\right)^2-5\left(\frac{5}{4}\right)-25=\frac{25}{8}-\frac{25}{4}-25=-\frac{225}{8}=-28\frac{1}{8}\end{align*}$
::x=522=54 现在,找到y=2( 542)-5(54)-2-5(25)-258-254-254-25522582818

The vertex is $\begin{align*}\left(\frac{5}{4}, -28\frac{1}{8}\right)\end{align*}$ . To graph this, we will need to estimate the vertex and draw an appropriate scale for the grid. As a decimal, the vertex is (1.25, -28.125).
::顶点是 (54,- 2818) 。要绘制这个图, 我们需要估计顶点, 并为网格绘制一个适当的比例。小数点后, 顶点是(1.25, - 28. 125) 。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the price point that will result in the maximum profit and to find the maximum profit.
::早些时候,你被要求找到能带来最大利润的价格点,并找到最大利润。

The maximum profit occurs that the maximum point of the parabola, so find the vertex of $\begin{align*}-3p^2 + 200p - 3000\end{align*}$ .
::最大利润是抛物线的最大点,因此找到3p2+200p-3000的顶点。

To find the vertex, use $\begin{align*}x=\frac{-b}{2a}\end{align*}$ .
::要找到顶点, 请使用 xb2a 。

$\begin{align*}x=\frac{-(200)}{2 \cdot -3}=\frac{-200}{-6}=33.33\end{align*}$ Plug this into the equation: $\begin{align*}y=(-3)(33.33)^2 +(200)(33.33) -3000=-3333+6667-3000=334\end{align*}$ .
::x(200)233226=33.33 将此插入方程中:y=(-3)(33.33)2+(200)(33.33)-3000*33+3667-3000=334。

Therefore, the vertex is (33.33, 334) and the maximum profit occurs at a price point of $33.33. At that price point, the profit would be $334.
::因此,顶点是(33.33,334美元),最高利润以33.33美元的价格点计算,在该价格点,利润为334美元。

Example 2
::例2

Find the $\begin{align*}x-\end{align*}$ intercepts, $\begin{align*}y-\end{align*}$ intercept, vertex, and axis of symmetry of $\begin{align*}y=-x^2+7x-12\end{align*}$ .
::查找 y*x2+7x- 12 的 X - 截取、 y - 截取、顶部和对称轴。

This is a factorable quadratic equation.
::这是一个可乘因数二次方程式。

$\begin{aligned} - (x^{2} - 7 x + 12) & = 0 \\ - (x^{2} - 3 x - 4 x + 12) & = 0 \\ - [x (x - 3) - 4 (x - 3)] & = 0 \\ - (x - 3) (x - 4) & = 0 \end{aligned}$
$\begin{align*}-(x^2-7x+12) &=0\\ -(x^2-3x-4x+12) &=0\\ -[x(x-3)-4(x-3)] &=0\\ -(x-3)(x-4) &=0\end{align*}$
::- (x2-7x+12)=0-(x2-3x-4x+12)=0-(x2-3x-4x+12)=0-[x(x)-3)-4(x-3)]=0-(x-3)(x-4)=0

The $\begin{align*}x-\end{align*}$ intercepts are (3, 0) and (4, 0).
::x- 拦截是(3,0)和(4,0)。

$\begin{aligned} y & = - 0^{2} + 7 (0) - 12 \\ y & = - 12 \end{aligned}$
$\begin{align*}y &=-0^2+7(0)-12\\ y &=-12\end{align*}$
::y#02+7(0)- 12y @% 12

The $\begin{align*}y-\end{align*}$ intercept is (0, -12).
::y - 拦截是( 0, - 12) 。

The $\begin{align*}x-\end{align*}$ coordinate of the vertex is $\begin{align*}x=\frac{-7}{2(-1)}=\frac{7}{2}\end{align*}$ . The $\begin{align*}y-\end{align*}$ coordinate is $\begin{align*}y=-\left(\frac{7}{2}\right)^2+7\left(\frac{7}{2}\right)-12=\frac{1}{4}\end{align*}$ .
::顶端的 x - 坐标是 x 72( - 1) = 72。 y - 坐标是 y ( 722) + 7( 72) - 12= 14 。

Therefore, the vertex is $\begin{align*}\left(\frac{7}{2}, \frac{1}{4}\right)\end{align*}$ and the parabola opens down because $\begin{align*}a<0\end{align*}$ . The axis of symmetry is $\begin{align*}x=\frac{7}{2}\end{align*}$ .
::因此,顶部是(72,14),抛物线打开是因为 <0。对称轴是 x=72。

Example 3
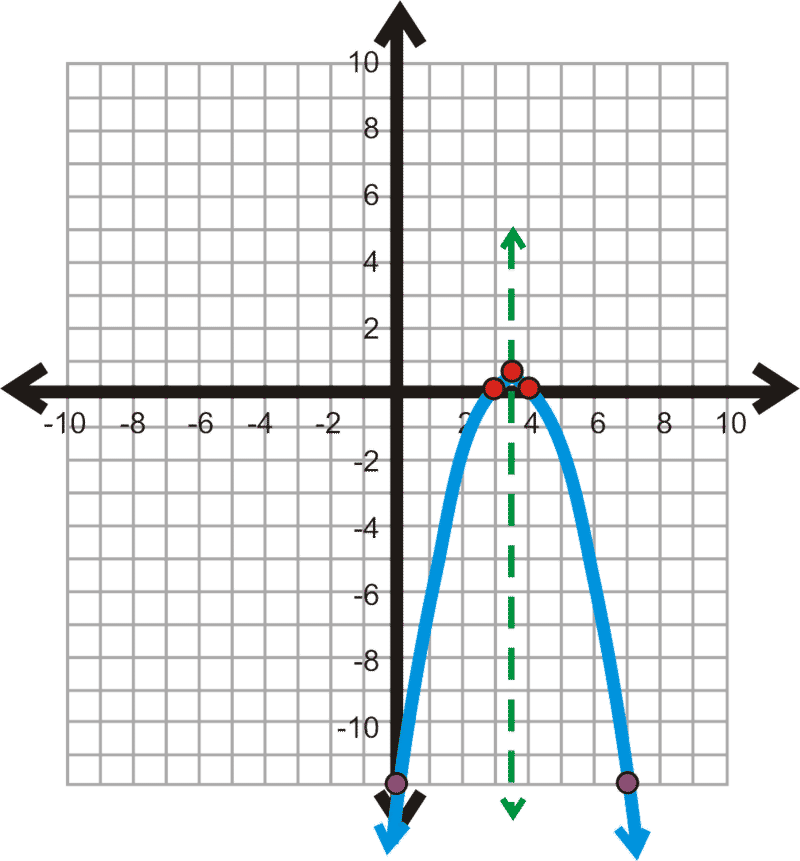
::例3

Sketch a graph of the parabola from Example 2.
::从例2中绘制抛物线图。

Plot all the points you found in Example 2. Then, connect the points to create the parabola.
::绘制您在例2中发现的所有点, 然后连接这些点以创建抛物线。

Example 4
::例4

Find the vertex of $\begin{align*}y=-4x^2+16x-17\end{align*}$ . Does the parabola open up or down?
::找到 y4x2+16x-17 的顶点。抛物线是向上还是向下打开吗 ?

First, the parabola opens down because $\begin{align*}a\end{align*}$ is negative. The $\begin{align*}x-\end{align*}$ coordinate of the vertex is $\begin{align*}x=\frac{-16}{2(-4)}=\frac{-16}{-8}=2\end{align*}$ . The $\begin{align*}y-\end{align*}$ coordinate is $\begin{align*}y=-4(2)^2+16(2)-17=-16+32-17=-1\end{align*}$ . This makes the vertex (2, -1).
::首先, parbola 向下打开, 因为一个是负的。顶端的 x - 坐标是 x 162( - 4) 16-8=2. y - 坐标是 y 4 (2) 2+16 (2) - 17 16+32 - 17 1. 。这就形成了顶端 ( 2, 1) 。

Even though the problem does not ask, we can infer that this parabola does not cross the $\begin{align*}x-\end{align*}$ axis because it points down and the vertex is below the $\begin{align*}x-\end{align*}$ axis. This means that the solutions would be imaginary.
::尽管问题并不要求,但我们可以推断,这个抛物线没有跨过 x - 轴,因为它指向下,顶部低于 x - 轴,这意味着解决办法是想象的。

Review
::回顾

Find the vertex of each parabola and determine if it is a maximum or minimum.
::查找每个抛物线的顶部并确定它是最大还是最小。

$\begin{align*}y=x^2-12x+11\end{align*}$
::y=x2 - 12x+11 y=x2 - 12x+11

$\begin{align*}y=x^2+10x-18\end{align*}$
::y=x2+10x- 18

$\begin{align*}y=-3x^2+4x+17\end{align*}$
::y3x2+4x+17

$\begin{align*}y=2x^2-9x-11\end{align*}$
::y= 2x2- 9x- 11 y= 2x2- 9x- 11

$\begin{align*}y=-x^2+6x-9\end{align*}$
::yx2+6x- 9

$\begin{align*}y=-\frac{1}{4}x^2+8x-33\end{align*}$
::y14x2+8x-33

Find the vertex, $\begin{align*}x-\end{align*}$ intercepts, $\begin{align*}y-\end{align*}$ intercept, and axis of symmetry of each factorable quadratic equation below. Then, sketch a graph of each one.
::查找顶部、 x - 截面、 y - 截面, 以及以下每个可因数二次方程的对称轴。然后绘制每个方程式的图示。

$\begin{align*}y=x^2-12x+11\end{align*}$
::y=x2 - 12x+11 y=x2 - 12x+11

$\begin{align*}y=-2x^2-5x+12\end{align*}$
::y2x2 - 5x+12

$\begin{align*}y=\frac{1}{3}x^2+4x-15\end{align*}$
::y= 13x2+4x- 15

$\begin{align*}y=3x^2+26x-9\end{align*}$
::y= 3x2+26x- 9

$\begin{align*}y=-x^2+10x-25\end{align*}$
::yx2+10x- 25

$\begin{align*}y=-\frac{1}{2}x^2+5x+28\end{align*}$
::y12x2+5x+28

If a function is not factorable, how would you find the $\begin{align*}x-\end{align*}$ intercepts?
::如果函数不是因数,您将如何找到 X - 界面 ?

Find the vertex and $\begin{align*}x-\end{align*}$ intercepts of the following quadratic equations. Then, sketch the graph. These equations are not factorable.
::查找以下二次方程的顶点和 x- intercut 。然后, 绘制图形。这些方程是不可计数的。

$\begin{align*}y=-x^2+8x-9\end{align*}$
::yx2+8x- 9

$\begin{align*}y=2x^2-x-8\end{align*}$
::y=2x2-x-8

Complete the table of values for the quadratic equations below. Then, plot the points and graph.
::完成以下二次方程的数值表。然后绘制点和图。

$\begin{align*}y=x^2-2x+2\end{align*}$ , x = 5, 3, 1, -1, -3, and -5
::y=x2-2x+2, x = 5, 3, 1, 1, 1, 3, 和 - 5

$\begin{align*}y=x^2+4x+13\end{align*}$ , x = 4, 0, -2, -4, and -8
::y=x2+4x+13, x=4, 0, 2, 4, 4和 -8

Writing What do you notice about the two parabolas from 16 and 17? What type of solutions do these functions have? Solve #16.
::您在写关于 16 和 17 的两种parabolas 上注意到什么? 这些函数有什么类型的解决方案? 解决 # 16 。

Writing How many different ways can a parabola intersect the $\begin{align*}x-\end{align*}$ axis? Draw parabolas on an $\begin{align*}x-y\end{align*}$ plane to represent the different solution possibilities.
::写入一个抛物线能够将 x - 轴相交多少种不同的方式? 在 x - y 平面上绘制 parabolas 来代表不同的解决方案。

Challenge If the $\begin{align*}x-\end{align*}$ coordinate of the vertex is $\begin{align*}\frac{-b}{2a}\end{align*}$ for $\begin{align*}y=ax^2+bx+c\end{align*}$ , find the $\begin{align*}y-\end{align*}$ coordinate in terms of $\begin{align*}a, b,\end{align*}$ and $\begin{align*}c\end{align*}$ .
::如果顶端的x- 坐标是y= ax2+bx+c的- b2a, 则用 a、 b 和 c 来查找 y- 坐标。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

查找帕拉波拉的部分

Parts of a Parabola ::帕拉波拉部分

Finding the Vertex of a Parabola ::找到帕拉波拉的顶点

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Parts of a Parabola
::帕拉波拉部分

Finding the Vertex of a Parabola
::找到帕拉波拉的顶点

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)