1.9 无限和不存在的限制

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 无限和不存在的限制

  Collapse Expand

  无限和不存在的限制

  播放段落

  You have heard time and again that it is "against the rules" to divide by the number 0 . Even the most basic calculator will return some form of "ERROR" if you try to divide even the smallest of numbers by 0 .
  ::您一再听到, 将数字除以 0 是“ 违反规则 ” 。 即使最基本的计算器也会返回某种形式的“ ERROR ” , 如果您试图将最小的数字除以 0 。

  播放段落

  Do you really understand why it is "against the rules"? What is really wrong with dividing by nothing?
  ::你真的明白为什么"违反规则"吗?

  播放段落

  Infinite and Non-Existent Limits
  ::无限和不存在的限制

  播放段落

  Functions can exhibit a number of different behaviors as the input value gets very large or very small.
  ::随着输入值变得非常大或非常小,函数可以显示若干不同的行为。

  播放段落

  As $\begin{array}{r}x\end{array}$ approaches $\begin{array}{r}\mathrm{\infty }\end{array}$ , some functions output values get closer and closer to a single number, some approach zero, and some continue to get larger and larger or smaller and smaller without limit.
  ::作为x 方法,有些函数输出值越来越接近单一数字,有些接近零,有些继续变大,有的变小,有的变小,没有限制。

  播放段落

  In this lesson, we will explore functions of the last type, functions with , and the different types of asymptotes they may have.
  ::在这一教训中,我们将探讨最后类型的功能、与......有关的功能以及它们可能具有的不同种类的微粒。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a question about dividing by zero.
  ::早些时候,你被问到 零除以零的问题。

  播放段落

  Dividing by zero is "against the rules" because there is no definition for the answer you would get.
  ::以零为分数是“违反规则”,因为没有定义你会得到的答案。

  播放段落

  Consider what happens as you take a given value and divide it by smaller and smaller numbers:
  ::考虑一下当您取一个给定值并用小数和小数除以该值时会发生什么:

  2 / 10 = 1/5

  2 / 1 = 2

  2 / .1 = 20

  2 / .001 = 2,000

  2 / .000000001 = 2,000,000,000

  播放段落

  As we divide by progressively smaller numbers, the quotient gets larger and larger. Also, we can see that in each case, the problem could be reversed by multiplying the product by the dividend to get the divisor, for instance: 2 / .1 = 20 ==> 20 * .1 = 2.
  ::随着我们以数量逐渐减少而分化,商数会越来越大。此外,我们可以看到,在每一种情况下,问题都可以通过将产品乘以红利来得到分数来扭转,例如:2 / 1 = 20 = 20 * = 2 = 20 * = 2 = 20 = 1 = 2。

  播放段落

  Unfortunately, this doesn't work if you actually divide by 0, even if you assume that dividing by zero resulted in infinity! No matter how big the number you multiply by zero, even infinity, you will never be able to get back to 2.
  ::不幸的是,如果你实际除以0,这行不通, 即使你假设除以零会导致无穷! 无论你乘以多少乘以零, 即使是无穷, 你都永远无法回到2。

  播放段落

  $\begin{array}{r}\therefore \frac{x}{0}=undefined\end{array}$
  ::x0=未定义

  播放段落

  Example 2
  ::例2

  播放段落

  Evaluate the function $\begin{array}{r}h(x)=\frac{x^2}{2x-1}\end{array}$ .
  ::评估函数 h( x) =x22x- 1。

  

  播放段落

  To evaluate this function, consider the behavior of the function as larger and larger values are inserted for x . As x approaches $\begin{array}{r}\mathrm{\infty }\end{array}$ , the function values also approach $\begin{array}{r}\mathrm{\infty }\end{array}$ . Therefore the limit of the function as x approaches $\begin{array}{r}\mathrm{\infty }\end{array}$ is: $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}\frac{x^2}{2x-1}=\mathrm{\infty }\end{array}$ . Similarly, as x approaches $\begin{array}{r}-\mathrm{\infty }\end{array}$ , f ( x ) approaches $\begin{array}{r}-\mathrm{\infty }\end{array}$ . Therefore we have $\begin{array}{r}\underset{x\to -\mathrm{\infty }}{lim}\frac{x^2}{2x-1}=-\mathrm{\infty }.\end{array}$
  ::要评估此函数, 请将函数的行为作为 x. x 的数值来考虑。 x 的 方针 * * , 函数值也接近 * 。 因此, x 方针 的函数限制是 : limx x22x- 1 。 同样, 如 x 方针 * , f (x) 方针 * 。 因此, 我们有 limx xx22x- 1 。

  播放段落

  We can also understand this limit if we analyze the equation for h ( x ). As x gets larger and larger, the value of the expression 2 x - 1 gets closer and closer to the value of the expression 2 x . That is, for sufficiently large values of x , 2 x - 1 $\begin{array}{r}\approx \end{array}$ 2 x . Therefore the values of h ( x ) approach $\begin{array}{r}\frac{x^2}{2x}=\frac{x}{2}\end{array}$ . As x gets larger and larger, so does $\begin{array}{r}\frac{x}{2}\end{array}$ . For large values of x , the function h ( x ) gets closer and closer to $\begin{array}{r}\frac{x}{2}\end{array}$ . Therefore the limit is infinity.
  ::如果分析 h(x) 的方程,我们也可以理解这个限制。随着 x 的扩大和增加,表达式 2x - 1 的值接近和接近表达式 2x 的值。也就是说,对于 X 的足够大的值, 2x - 1 2x。 因此, 当 x 的扩大和增加时, h(x) 的值是 x 22x=x2 的值。 对于 x 的大值, 函数 h(x) 的值越来越接近和接近 x2 的值, 因此, 限制是无限的 。

  播放段落

  Example 3
  ::例3

  播放段落

  Approximate the function f ( x ) = x ² + 2 x - 3.
  ::函数 f( x) = x2 + 2x - 3 近似于函数 f( x) = x2 + 2x - 3 。

  播放段落

  This function has an infinite limit as x approaches infinity. However, as x gets larger and larger, f ( x ) $\begin{array}{r}\approx \end{array}$ x ² , since the x ² value grows much more quickly than the 2 x value, particularly apparent at very large +/- values of x . If this is not immediately apparent, evaluate the function for x = 1,000,000, and you will quickly get the idea!
  ::3⁄4 ̄ ̧漯B

  播放段落

  Therefore we can use the function y = x ² to describe the end behavior of f ( x ).
  ::因此,我们可以使用函数 y = x2 来描述 f( x) 的结束行为 。

  播放段落

  Example 4
  ::例4

  播放段落

  Describe the end behavior of each graph. That is, determine if the function has a limit L , if the limit is infinite, or if the limit does not exist .
  ::描述每个图形的结束行为。 也就是说, 确定函数是否有限制 L, 是否限制是无限的, 或者限制不存在 。

  播放段落
  1. $\begin{array}{r}y=x^2\end{array}$
     ::y=x2 y=x2

  播放段落

  As x approaches $\begin{array}{r}+\mathrm{\infty }\end{array}$ , x ² also approaches $\begin{array}{r}+\mathrm{\infty }\end{array}$ . As x approaches $\begin{array}{r}-\mathrm{\infty }\end{array}$ , x ² approaches $\begin{array}{r}+\mathrm{\infty }\end{array}$ . Therefore $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}{x}^2=\underset{x\to -\mathrm{\infty }}{lim}{x}^2=\mathrm{\infty }\end{array}$ .
  ::Asxoproaches,x2 also apploaches,x2 approaches,x2 approaches,soslimxx2=limxxxx2。

  播放段落
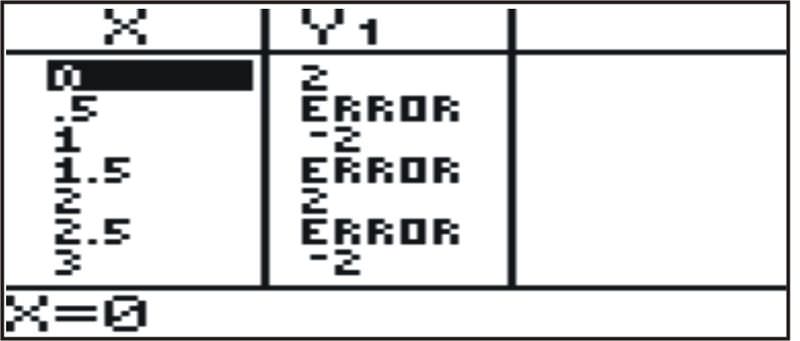
  2. $\begin{array}{r}y=2(-1{)}^x\end{array}$
     ::y=2 (- 1) x

  播放段落

  This function is difficult to understand without producing a graph. The table shows that the function only takes on two values: 2, and -2, and is undefined at non-integer values of x . As x approaches $\begin{array}{r}+\mathrm{\infty }\end{array}$ or $\begin{array}{r}-\mathrm{\infty }\end{array}$ , the function values alternate between 2 and -2. Therefore the limit does not exist.
  ::3⁄4 ̄ ̧漯B

  

  播放段落
  3. $\begin{array}{r}y=1-\frac{1}{|x|}\end{array}$
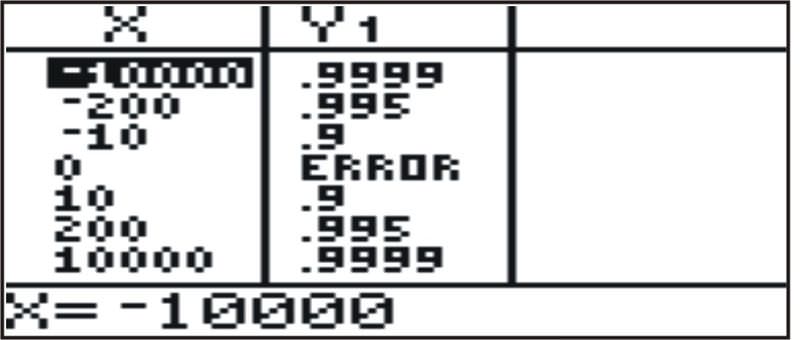
     ::y=1 - 1x

  播放段落

  If you look at the table of this function, which has negative and positive values of x , you can see that as x approaches $\begin{array}{r}+\mathrm{\infty }\end{array}$ or $\begin{array}{r}-\mathrm{\infty }\end{array}$ , the function values approach 1.
  ::如果您查看此函数的表格,该表含有 x 的负值和正值,您可以看到,作为 x 接近 {{{} 或{} ,函数值取 1。

  

  播放段落

  Therefore $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}\left(1-\frac{1}{|x|}\right)=\underset{x\to -\mathrm{\infty }}{lim}\left(1-\frac{1}{|x|}\right)=1\end{array}$ .
  ::因此, limx( 1 - 1 x) =limx( 1 - 1 x) = 1 。

  播放段落

  We can also determine this limit analytically . For large values of x , | x | is also large, and so $\begin{array}{r}\frac{1}{|x|}\end{array}$ is small (since dividing 1 by a large number results in a very small number). Therefore, for large values of x , $\begin{array}{r}1-\frac{1}{|x|}\approx 1-0=1\end{array}$ . We can make the same argument for x approaching $\begin{array}{r}-\mathrm{\infty }\end{array}$ .
  ::也可以用分析方式确定此限值 。 对于 x 的大值, x 也很大, 所以 1x 很小( 因为除以 1 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 以一 。 对于 x 的大值, 我们可以为 x 的接近提出相同的论据 。

  播放段落

  Example 5
  ::例5

  播放段落

  Evaluate $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}\frac{x^2+2x}{x-3}\end{array}$ .
  ::评估 limxx2+2xx_3 。

  播放段落

  T he numerator is of greater degree than the denominator, so the function does not approach a limit. The denominator is x - 3 , so the graph cannot include 3 .
  ::分子比分母要大得多, 所以函数不会接近极限 。 分母 isx - 3 无法在图形中包含 3 。

  播放段落

  Example 6
  ::例6

  播放段落

  Evaluate $\begin{array}{r}-2x^3-5x^2+8x\end{array}$ .
  ::评价-2x3-5x2+8x。

  播放段落

  $\begin{array}{r}-2x^3-5x^2+8x\end{array}$ is a 3rd degree equation, so it will turn twice, since it is not a rational function, there are no concerns about numerator or denominator. The function will have no limits, and will grow without bound in both the positive and negative directions. If you use a graphing calculator to graph the function, you will see that $\begin{array}{r}y=x^3\end{array}$ can be used to approximate it.
  ::2- 2x3- 5x2+8x 是 3 度方程式, 因此它会翻转两次, 因为它不是一个合理函数, 对分子或分母没有顾虑 。 该函数将没有限制, 并且不会在正向和负方向下同时增长。 如果您使用图形计算器来绘制函数图, 你会看到 y=x3 可以用来接近函数 。

  播放段落

  Review
  ::回顾

  播放段落
  1. Give an example of a limit that does not exist
     ::举一个不存在的限制的示例

  播放段落

  Questions  5-7: Assuming that $\begin{array}{r}f(x)\end{array}$ is a rational function:
  ::问题5-7:假设f(x)是一个合理功能:

  播放段落
  2. What is $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}f(x)\end{array}$ when the degree of the numerator is less than the degree of the denominator?
     ::当分子的程度小于分母的程度时, limxf(x) 是什么 ?
  播放段落
  3. What is $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}f(x)\end{array}$ when the degrees of the numerator and the denominator are equal?
     ::当分子和分母的度相等时, limxf(x) 是什么 ?
  播放段落
  4. What is $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}f(x)\end{array}$ when the degree of the numerator is greater than the degree of the denominator?
     ::当分子的程度大于分母的程度时, limxf(x) 是什么 ?

  播放段落
  5. In general, if r is a positive real number, what is $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}\frac{1}{x^r}\end{array}$ ?
     ::一般而言,如果r是正数,那么何为正数?
  播放段落
  6. In general, if r is a positive real number, what is $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}{x}^r\end{array}$ ?
     ::一般而言,如果r是正数,那么何为正数?

  播放段落

  Questions  10-13: Let a and b be real numbers and let t be a positive integer. Complete each of the following properties of limits.
  ::问题10-13:让a和b为实际数字,而不要为正整数。填写以下每种限制的属性。

  播放段落
  7. $\begin{array}{r}\underset{x\to a}{lim}{x}^t=\end{array}$
     ::立方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平方平面=
  播放段落
  8. If f is a polynomial, $\begin{array}{r}\underset{x\to a}{lim}f(x)=\end{array}$
     ::如果 f 是多元的, limxaf(x) =
  播放段落
  9. $\begin{array}{r}\underset{x\to a}{lim}k\cdot f(x)=\end{array}$
     ::立方厘米( x) =
  播放段落
  10. $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}{t}^x=\end{array}$
      ::limxtx=

  播放段落

  Questions  14-16: Evaluate.
  ::问题14-16:评价。

  播放段落
  11. $\begin{array}{r}\underset{x\to -5}{lim}\frac{(5+x{)}^2-25}{x}\end{array}$
      ::limx%5( 5+x) 2-2- 25x
  播放段落
  12. $\begin{array}{r}\underset{x\to 3}{lim}\frac{x^3-6x+2}{x^2+2x-3}\end{array}$
      ::limx=3x3 - 6x+2x2+2x- 3

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。