1.11 广场和立方体功能家庭

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节广场和立方体功能家庭

  折叠 展开

  广场和立方体功能家庭

  播放段落

  Often, the most challenging part of completing a math problem is just getting started. Once you have a 'feel' for how a particular problem should be solved, crunching the numbers is generally not very difficult.
  ::通常,完成数学问题最具挑战性的部分只是刚刚开始。 一旦你对如何解决某个特定问题有了“感觉 ” , 压缩数字通常并不难。

  播放段落

  An understanding of function families can be a big help with this, as it gives you an idea of what a more complex function should look like once it has been graphed, just by identifying the parent or most simplified version of the function.
  ::了解功能家庭可以大有帮助,因为它能让大家知道,一旦绘制出图表,一个更复杂的功能会是什么样子,只需确定该函数的父/母或最简化的版本。

  播放段落

  Do you know the parent functions for the Square, Cube, Square Root , and Reciprocal function families?
  ::您知道平方、立方、平方根和对等功能家庭的父母函数吗?

  播放段落

  Square and Cube Function Families
  ::广场和立方体功能家庭

  播放段落

  Function Family: Square Functions
  ::函数家庭:平方函数

  播放段落

  A square function is a 2nd degree equation , meaning it has an x ² .
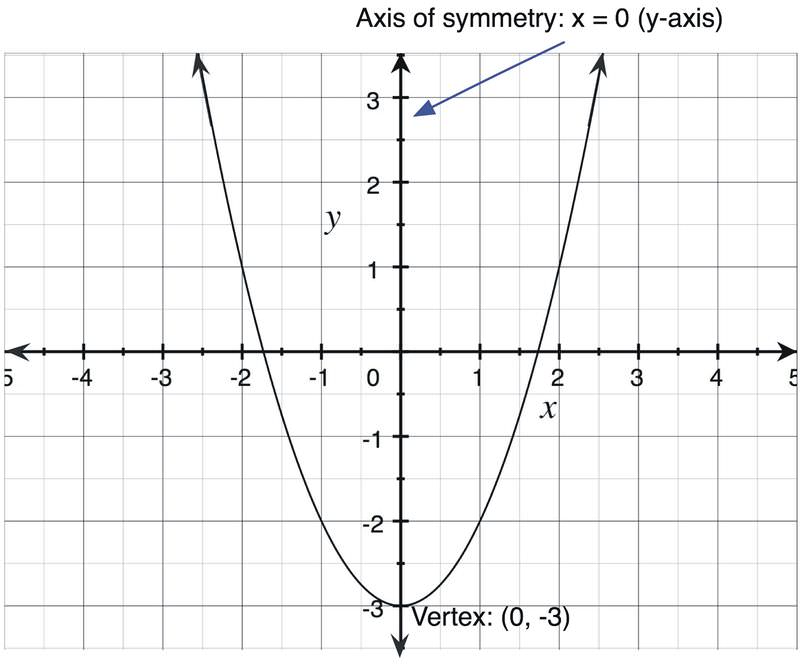
  ::方形函数是二度方程式,意思是它有一个 x2 。

  播放段落

  The graph of every square function is a parabola . A parabola has a vertex , and an axis of . The graph below shows these aspects of the graph of y = x ² - 3.
  ::每个平方函数的图形是抛物线。 抛物线有一个顶点和一个轴。 下图显示了 y = x2 - 3 的图形的这些方面。

  

  播放段落

  Function Family: Cubic Functions
  ::函数家族:立体函数

  播放段落

  A cube function is a third-degree equation: x ³ and which does not contain negative or . In general, the graphs of cube functions have a particular shape, illustrated by the graph shown here:
  ::立方体函数是三度方程式: x3, 不含负数或 。 一般而言, 立方体函数的图形有特定形状, 此处显示的图形可以说明 :

  

  播放段落

  Cubic functions have a similar shape. However, only some cubic functions will have a relative maximum and minimum. For example, the graph of y = ( x - 2) ³ - 5 x shown above, has a relative maximum around x = 0.7, and a relative minimum around x = 3.3. The shape of the cubic graph means that we can predict end behavior: one end will approach $\begin{array}{r}\mathrm{\infty }\end{array}$ , and the other will approach $\begin{array}{r}-\mathrm{\infty }\end{array}$ .
  ::立方体函数的形状相似。 但是, 只有某些立方体函数将具有相对的上限和最小值。 例如, y = (x - 2)3 - 5x 的图形显示为 y = (x - 2) = 0. 7 的相对上限, 和 x = 3. 3 的相对最小值。 立方体图形的形状表示我们可以预测最终行为: 一方接近 + , 另一方接近 \ 。

  播放段落

  It is important to note here that the cubic function grows faster than an associated quadratic function . For example, y = x ³ grows faster than y = x ² .
  ::在此必须指出, 立方函数的生长速度比相关二次函数的生长速度要快。 例如, y = x3 的生长速度比 y = x2 的生长速度要快 。

  播放段落

  Function Family: Square Root Functions
  ::函数家庭:平根函数

  播放段落

  Consider the parent of the family, $\begin{array}{r}y=\sqrt{x}\end{array}$ . The domain of the function is limited to real numbers ≥ 0, as the square root of a negative number is not a real number . Similarly, the range of the function is limited to real numbers ≥ 0. This may seem confusing if you think of squares having two roots. For example, 9 has two roots: 3, and -3. However, for $\begin{array}{r}y=\sqrt{x}\end{array}$ , we have to define the function value as the principal root , which means the positive root.
  ::y=x。 函数的域限为 = 0, 因为负数的平方根不是一个实际数字。 同样, 该函数的范围也限为 = 0。 如果您认为正方根有两个根, 这可能令人困惑。 例如, 9 有两根根 : 3 和 - 3 。 但是, y=x 的域, 我们必须将函数值定义为主根, 这意味着正根 。

  播放段落

  The function $\begin{array}{r}y=\sqrt{x}\end{array}$ is shown below:
  ::函数 y=x 显示如下:

  

  播放段落

  The same kind of limitations of will exist for any square root function .
  ::任何平方根函数都存在同样的意志限制。

  播放段落

  Function Family: Reciprocal Functions
  ::函数家庭:对等职能

  播放段落

  The function $\begin{array}{r}y=\frac{1}{x}\end{array}$ has a rather surprising graph. First, the domain cannot include 0, as the fraction $\begin{array}{r}\frac{1}{0}\end{array}$ is undefined . The range also does not include 0, as a fraction can only be zero if the numerator is zero, and the numerator of $\begin{array}{r}y=\frac{1}{x}\end{array}$ is always 1.
  ::y=1x 函数有一个相当令人惊讶的图形。 首先, 域不能包含 0, 因为分数 10 是未定义的。 范围也不包括 0, 因为如果分子为零, 分数只能为零, 而 y=1x 的分子总是 1 。

  播放段落

  In order to understand what these limitations mean for the graph, we will consider function values near x = 0 and y = 0. First, consider very small values of x . For example, consider x = 0.001. This yields $\begin{array}{r}y=\frac{1}{x}=\frac{1}{0.001}=1000\end{array}$ . As we get closer and closer to x = 0, the function values approach $\begin{array}{r}\mathrm{\infty }\end{array}$ . On the other side of the x -axis the function values will approach $\begin{array}{r}-\mathrm{\infty }\end{array}$ . We can see this behavior in the graph as a vertical asymptote : the graph is asymptotic to the y -axis.
  ::为了理解这些限制对图形意味着什么, 我们将考虑接近 x = 0 和 y = 0 的函数值。 首先, 考虑 x 的非常小的值。 例如, 考虑 x = 0.001 。 这样得出 y= 1x= 10. 001 =1000 。 当我们接近 x = 0 时, 函数值 方针 。 在 x 轴的另一边, 函数值会接近 。 我们可以在图表中将这个行为看成一个垂直的无线 : 图表对 y 轴是无线的 。

  播放段落

  We can also see in the graph that as x approaches $\begin{array}{r}+\mathrm{\infty }\end{array}$ or $\begin{array}{r}-\mathrm{\infty }\end{array}$ , the function values approach 0. The exclusion of y = 0 from the range means that the function is asymptotic to the x -axis.
  ::我们也可以在图表中看到,当 x 接近\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Y=0\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a question about identifying the parent functions of various function families.
  ::早些时候,有人问您如何确定不同功能家庭的父母职能。

  播放段落

  Can you identify the parent functions of the square, cube, square root, and reciprocal functions now?
  ::您现在能够辨别正方形、立方体、平方根和对等函数的父函数吗?

  播放段落

  Square: $\begin{array}{r}y=x^2\end{array}$
  ::平方: y=x2

  播放段落

  Cube: $\begin{array}{r}y=x^3\end{array}$
  ::立方: Y=x3

  播放段落

  Square Root: $\begin{array}{r}y=\sqrt{x}\end{array}$
  ::平方根: Y=x

  播放段落

  Reciprocal: $\begin{array}{r}y=1/x\end{array}$
  ::互惠:y=1/x

  播放段落

  Learning the function families is one of the fastest way to graph complex equations. Using parent functions and transformations (which are detailed in another set of lessons), you can graph very complex equations rather easily.
  ::学习函数家庭是绘制复杂方程式的最快方法之一。使用父函数和转换(在另一套课程中详述),您可以很容易地绘制非常复杂的方程式。

  播放段落

  Example 2
  ::例2

  播放段落

  Describe the end behavior of each function, and identify the parent function for each.
  ::描述每个函数的最终行为, 并确定每个函数的父函数 。

  播放段落
  1. y = x ² - 1
     ::y = x2 - 1 = x2 - 1

  播放段落

  The parent of this function is y = x ² .
  ::此函数的母值是 y =x2。

  播放段落

  The graph of this function is a parabola that opens up. Therefore $\begin{array}{r}\underset{x\to \pm \mathrm{\infty }}{lim}(x^2-1)=\mathrm{\infty }\end{array}$ .
  ::此函数的图形是一个打开的抛物线。因此, limx(x2- 1)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\>\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落
  2. y = - x ² + 1
     ::y = -x2 + 1

  播放段落

  The parent of this function is y = x ² .
  ::此函数的母值是 y = x2。

  播放段落

  The graph of this function is a parabola that opens down. Therefore $\begin{array}{r}\underset{-x\to \pm \mathrm{\infty }}{lim}(x^2-1)=-\mathrm{\infty }\end{array}$ .
  ::此函数的图形是一个打开的抛物线。因此, lim-x(x2- 1)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  All square functions have either a global maximum or minimum. The location of the maximum or minimum is always the vertex of the parabola. Square functions also share behavior in terms of their average rate of change . Consider for example the functions f ( x ) = x ² , g ( x ) = x ² - 3 , and g ( x ) = 2 x ² - 3. The table below shows the average rate of change (ARC) of each function on several intervals.
  ::所有正方形函数都具有全球最大值或最小值。 最大值或最小值的位置始终是抛物线的顶点。 方形函数也根据其平均变化速度而共享行为。 例如, 函数 f( x) = x2, g( x) = x2 - 3, g( x) = x2 - 3, g( x) = 2x2 - 3. 下表显示每个函数的平均变化率( ARC) 。

  播放段落

  Note: The ARC of a function on the interval (a, b) is $\begin{array}{r}\frac{f(b)-f(a)}{b-a}\end{array}$ .
  ::注:间距(a,b)的函数(f(b)-f(a)b-a)ARC。

  Interval	ARC of f ( x )	ARC of g ( x )	ARC of h ( x )
  (-1, 0)
  (0, 1)	1	1	2
  (1, 2)	3	3	6
  (2, 3)	5	5	10

  

  播放段落

  Notice that the average rate of change of f ( x ) and g ( x ) is the same on each interval, and the average rate of change of h ( x ) is twice that of the other two functions. You may also notice that the average rate of change follows a linear pattern : on each interval the rate increases at a constant rate of 2. While have a constant rate of change, quadratic functions have an average rate of change that follows a linear pattern.
  ::请注意 f( x) 和 g( x) 的平均变化率每间隔相同, h( x) 的平均变化率是另外两个函数的两倍。 您还可以注意到,平均变化率遵循线性模式: 每个间隔的利率增长率以恒定速度为2. 二次函数虽然变化率不变,但按照线性模式的平均变化率。

  播放段落

  Example 3
  ::例3

  播放段落

  Graph the function $\begin{array}{r}y=\sqrt{3-x}+1\end{array}$ , identify the parent function, and state the domain and range of the function.
  ::绘制函数 y=3 - x+1 的图形,标明父函数,并标明函数的域和范围。

  播放段落

  The parent function is $\begin{array}{r}y=\sqrt{x}\end{array}$
  ::父函数 Y=x

  

  播放段落

  From the graph you can see that the function does not take on any x values above 3. (Why not?) Therefore the domain is limited to real numbers ≤ 3. The function’s lowest value is 1, so the range is limited to all real numbers ≥ 1 .
  ::从图表中可以看到,函数没有吸收3以上的任何 x 值(为什么不? ) 。 因此,域限为 = = = 3. 函数的最低值为 1, 因此范围限于所有 = 1 = 1 。

  播放段落

  It is important to note that while the graph of a square root function might look as if it has horizontal asymptote , it does not. The function values will grow without bound (though relatively slowly!).
  ::需要注意的是,平方根函数的图形可能看起来像平方根函数的平面小数,但它没有。 函数值将不受约束地增长( 尽管相对缓慢 ! ) 。

  播放段落

  Example 4
  ::例4

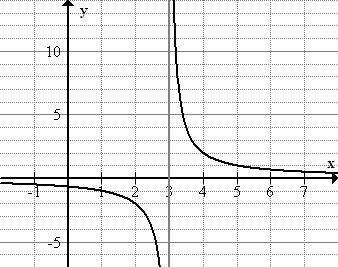
  播放段落

  Graph the function $\begin{array}{r}f(x)=\frac{2}{x-3}\end{array}$ , identify the parent function, and identify horizontal and vertical asymptotes .
  ::函数 f( x) = 2x- 3 的图形, 标明父函数, 并标明水平和垂直的单位数 。

  播放段落

  The parent function is $\begin{array}{r}y=1/x\end{array}$
  ::父函数为 Y=1/x

  

  播放段落

  The graph is asymptotic to the x -axis ( y = 0) and to the line x = 3.
  ::该图对 x 轴(y = 0) 和 线x = 3 表示无症状。

  播放段落

  Example 5
  ::例5

  播放段落

  Identify the parent function within the following  set of functions. Graph the  set of functions using a graphing calculator. Identify similarities and differences of the set.
  ::确定以下一组函数中的父函数。使用图形计算器绘制函数组。确定集的相似和不同之处。

  $\begin{array}{r}f(x)=x^2-10\end{array}$	$\begin{array}{r}f(x)=x^2-1\end{array}$	$\begin{array}{r}f(x)=x^2\end{array}$
  $\begin{array}{r}f(x)=x^2+3\end{array}$	$\begin{array}{r}f(x)=x^2+9\end{array}$

  

   

  播放段落
  1. Parent Function:  The parent function of this group of quadratic functions is the most basic function in the set: $\begin{array}{r}f(x)=x^2\end{array}$
     ::父函数 父函数 : 此类二次函数组的父函数是集( f)( x) =x2 中最基本的函数 。

  播放段落
  2. Similarities: width, shape, end behavior, and degree
     ::相似度:宽度、形状、结束行为和程度

  播放段落
  3. Differences:  x and y intercepts
     ::差异: xandy 界面

  播放段落

  Example 6
  ::例6

  播放段落

  Identify the parent function within the following set of functions. Graph the set of functions using a graphing calculator. Identify similarities and differences of the set.
  ::确定以下一组函数中的父函数。使用图形计算器绘制函数组。确定集的相似和不同之处。

  $\begin{array}{r}f(x)=(x+9{)}^3\end{array}$	$\begin{array}{r}f(x)=(x+2{)}^3\end{array}$	$\begin{array}{r}f(x)=x^3\end{array}$
  $\begin{array}{r}f(x)=(x-4{)}^3\end{array}$	$\begin{array}{r}f(x)=(x-8{)}^3\end{array}$

  

  播放段落
  1. Parent Function:  The parent function of this group of quartic functions is the most basic function in the set: $\begin{array}{r}y=x^3\end{array}$
     ::父函数 父函数 : y=x3 集中最基本函数是这组二次函数的父函数 : y=x3

  播放段落
  2. Similarities:  end behavior, domain and range, direction, and width
     ::相似点:最终行为、域和范围、方向和宽度

  播放段落
  3. Differences:  x and y intercepts, increasing and decreasing intervals
     ::差异:X和截取、增加和减少间隔

  播放段落

  Review
  ::回顾

  播放段落
  1. Explain what a square function is:
     ::解释一个平方函数是什么 :
  播放段落
  2. What is a cube function?
     ::什么是立方体函数?
  播放段落
  3. Describe the rate of growth of a cubic function related to the growth of a squared function
     ::描述与平方函数增长有关的立方函数的增长率
  播放段落
  4. For square root functions we have to define the function value as the positive root, also known as what?
     ::对于平方根函数,我们必须将函数值定义为正根, 也称为什么?
  播放段落
  5. Why are reciprocal functions asymptotic to the x-axis?
     ::为什么对等功能对 X 轴不起作用?

  播放段落

  Identify the parent function within each set of squared functions. Graph each set of functions using a graphing calculator. Identify similarities and differences of each set.
  ::确定每组平方函数中的父函数。 使用图形计算器绘制每组函数的图。 确定每组函数的相似性和差异 。

  播放段落

  Set 1:
  ::设定 1:

  $\begin{array}{r}f(x)=x^2-10\end{array}$	$\begin{array}{r}f(x)=x^2-1\end{array}$	$\begin{array}{r}f(x)=x^2\end{array}$
  $\begin{array}{r}f(x)=x^2+3\end{array}$	$\begin{array}{r}f(x)=x^2+9\end{array}$

  播放段落
  6. Set 1:
     ::设定 1:

  播放段落
  1. Parent Function:
     ::父函数 :
  播放段落
  2. Similarities:
     ::相似点:
  播放段落
  3. Differences:
     ::差异:

  播放段落

  Set 2:
  ::设定2:

  $\begin{array}{r}f(x)=(x+10{)}^2\end{array}$	$\begin{array}{r}f(x)=(x+4{)}^2\end{array}$	$\begin{array}{r}f(x)=x^2\end{array}$
  $\begin{array}{r}f(x)=(x-2{)}^2\end{array}$	$\begin{array}{r}f(x)=(x-5{)}^2\end{array}$

  播放段落
  7. Set 2:
     ::设定2:

  播放段落
  1. Parent Function:
     ::父函数 :
  播放段落
  2. Similarities:
     ::相似点:
  播放段落
  3. Differences:
     ::差异:

  播放段落

  Set 3:
  ::设定 3 :

  $\begin{array}{r}f(x)=-x^2\end{array}$	$\begin{array}{r}f(x)=x^2\end{array}$

  播放段落
  8. Set 3:
     ::设定 3 :

  播放段落
  1. Parent Function:
     ::父函数 :
  播放段落
  2. Similarities:
     ::相似点:
  播放段落
  3. Differences:
     ::差异:

  播放段落

  Use the above information and the vertex form of a quadratic equation: $\begin{array}{r}f(x)=a(x-h{)}^2+k\end{array}$ to help you answer the following questions:
  ::使用上述信息和二次方程的顶点形式: f(x)=a(x-h)2+k,帮助您回答下列问题:

  播放段落
  9. How does the a value affect the graph?
     ::此值如何影响图形 ?
  播放段落
  10. How does the h value affect the graph?
      ::h 值如何影响图形 ?
  播放段落
  11. How does the k value affect the graph?
      ::k 值如何影响图形 ?
  播放段落
  12. How are domain values similar/different?
      ::域值如何相似/不同?
  播放段落
  13. How are range values similar/different?
      ::范围值如何相似/不同?
  播放段落
  14. Does the a, h, and/or k value affect the domain?
      ::a、h和/或k值是否影响域名?
  播放段落
  15. Does the a, h, and/or k value affect the range?
      ::a、h和/或k值是否影响范围?

  播放段落

  Cubic Functions:
  ::立方函数 :

  播放段落

  Circle the parent function within each set of cubic functions. Graph each set of functions using a graphing calculator. Identify similarities and differences of each set.
  ::在每组立方函数中圆圆父函数。使用图形计算器绘制每组函数。确定每组函数的相似和不同之处。

  播放段落

  Set 4:
  ::设定4:

  $\begin{array}{r}f(x)=x^3-5\end{array}$	$\begin{array}{r}f(x)=x^3-3\end{array}$	$\begin{array}{r}f(x)=x^3\end{array}$
  $\begin{array}{r}f(x)=x^3+1\end{array}$	$\begin{array}{r}f(x)=x^3+6\end{array}$

  播放段落
  16. Set 4:
      ::设定4:

  播放段落
  1. Parent Function:
     ::父函数 :
  播放段落
  2. Similarities:
     ::相似点:
  播放段落
  3. Differences:
     ::差异:

  播放段落

  Set 5:
  ::设定 5 :

  $\begin{array}{r}f(x)=-x^3\end{array}$	$\begin{array}{r}f(x)=x^3\end{array}$

  播放段落
  17. Set 5:
      ::设定 5 :

  播放段落
  1. Parent Function:
     ::父函数 :
  播放段落
  2. Similarities:
     ::相似点:
  播放段落
  3. Differences:
     ::差异:

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。