Course: 2.10 一夫多妻制和理性不平等

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

多元和理性不平等

Often it is easier to use and remember new terms when you have a 'hook' or comparison to a term you know already.
::当您有一个“ 锁定” 或与您已经知道的术语比较时,使用和记住新术语通常比较容易。

" Polynomial inequality" is a term generally used to refer to inequalities where the x variable has a degree of 3 or greater.
::“世系不平等”一词通常用来指在x变量为3级或3级以上的情况下的不平等。

The prefix "poly" means 'multiple' or 'many', and the root word "nomial" means 'name' or 'term'.
::前缀“poly” 表示“ 多重” 或“ many ” , 根词“ 名” 表示“ 名称” 或“ term ” 。

Therefore a "polynomial" is literally: "many terms".
::因此,一个“政体”字面上是: “许多术语”。

The prefix "in" means 'not', and the root word "equal" of course means 'the same'.
::前缀“ in” 表示“ not” , 根字“ equal” 当然表示“ 相同 ” 。

Therefore and "inequality" refers to things which are "not same" or "not equal".
::因此,“不平等”是指“不同”或“不平等”的东西。

Can you use this logic to identify the origin of some of the other terms used in this lesson?
::您能否用这个逻辑来确定本课中使用的其他术语的来源?

Polynomial and Rational Inequalities
::多元和理性不平等

Polynomial Inequalities
::多元不平等

Solving polynomial inequalities is very similar to solving . The basic steps are the same:
::解决多元不平等与解决非常相似。

Set up the inequality in the form $\begin{aligned} p (x) > 0 \end{aligned}$ (or $\begin{aligned} p (x) < 0, p (x) \leq 0, p (x) \geq 0 \end{aligned}$ )
::设置 p( x) > 0 (或 p( x) < 0, p( x) =0, p( x) =0) 形式的不平等。

Find the solutions to the equation $\begin{aligned} p (x) = 0 \end{aligned}$ .
::查找公式p(x)=0的解决方案。

Divide the number line into intervals based on the solutions to $\begin{aligned} p (x) = 0 \end{aligned}$ .
::根据 p( x) =0 的解决方案将数字行除以间隔。

Use test points to find solution sets to the equation.
::使用测试点来寻找方程式的解决方案集。

Rational Inequalities
::理性不平等

There is one step added to the process of solving rational inequalities because a rational function can also change signs at its vertical asymptotes or at a break in the graph. For instance, look at the graph of the function $\begin{aligned} r (x) = \frac{x}{x^{2} - 9} \end{aligned}$ below.
::在解决合理不平等的过程中,增加了一个步骤,因为理性功能也可以改变其垂直微粒或图中断层的符号。例如,看看下面的 r(x) =x22-9 函数图。

If we want to solve the inequality $\begin{aligned} \frac{x}{x^{2} - 9} > 0 \end{aligned}$ , then we need to use the following critical points: $\begin{aligned} x = 0, x = 3, \end{aligned}$ and $\begin{aligned} x = - 3 \end{aligned}$ . $\begin{aligned} x = 0 \end{aligned}$ is the solution of setting the numerator equal to 0, and this gives us the only root of the function. $\begin{aligned} x = \pm 3 \end{aligned}$ are the vertical asymptotes, the $\begin{aligned} x - \end{aligned}$ coordinates that make the function undefined because putting in 3 or -3 for $\begin{aligned} x \end{aligned}$ will cause a division by zero.
::如果我们想要解决不平等问题xx2-9>0, 那么我们需要使用以下关键点 : x=0, x=3, 和 x3. x=0 是将分子设置为 0 的解决方案, 这给了我们函数的唯一根。 x\\ 3 是垂直的静态, x- 坐标使函数未定义, 因为将 x 插入 3 或 - 3 导致零分裂。

Testing the intervals between each critical point to see if the values in that interval satisfy the function gives us:
::测试每个临界点之间的间隔, 以确定该间隔中的值是否满足函数给我们的功能 :

Interval	Test Point	Positive/Negative?	Part of Solution Set?
$\begin{aligned} (- \infty, - 3) \end{aligned}$	-4	-	no
(-3, 0)	-2	+	yes
(0, 3)	2	-	no
$\begin{aligned} (3, + \infty) \end{aligned}$	4	+	yes

Thus, the solutions to $\begin{aligned} \frac{x}{x^{2} - 9} > 0 \end{aligned}$ are $\begin{aligned} x \in (- 3, 0) \cup (3, + \infty) \end{aligned}$ .
::因此,xx2-9>0的解决方案是 x(- 3,0)(3, )。

Examples
::实例

Example 1
::例1

Earlier, you were given a question about identifying the origins of other terms in this lesson.
::早些时候,有人问你们如何确定这一教训中其他术语的起源。

How many of the terms we have used recently were you able to track down the origins of? A few are listed below, did you find others?
::我们最近使用的术语中有多少是你们能够找到来源的?下面列出了几个词,你们找到其他词了吗?

Bi-nomial: "two-named" or "two-terms" - from "bi", meaning 'two' and "nomial", meaning 'name' or 'term'. Quad-ratic: "related to a square" - from "quadratus", meaning 'square'. Ratio-nal: "related to a ratio" - from "ratio", meaning 'reason' (as in "to reason" or "calculate") and "-al", meaning "related to".
::双名 : “ 两名 ” 或“ 两期 ” - 从“ 双 ” , 意谓“ 二 ” 和“ 名 ” , 意谓“ 名 ” 或“ 术语 ” 。四方 : “ 与一个正方形有关 ” , 意谓“ quadratus ” , 意谓“ quadratus ” 。有理 : “ 与比率有关 ” - 从“ ratio ” , 意谓“ 引因 ” (以“ 向理性 ” 或“ 计算 ” ) 和“ al ” 意谓“ 相关 ” 。

Example 2
::例2

Solve $\begin{aligned} x^{3} - 3 x^{2} + 2 x \geq 0 \end{aligned}$ .
::解决 x3 - 3x2+2x%0 。

The polynomial is already in the correct form $\begin{aligned} p (x) \geq 0 \end{aligned}$ so we solve the equation
::多多边性已经处于 p( x) =0 的正确形式中, 所以我们解析方程式

\begin{aligned} x^{3} - 3 x^{2} + 2 x & = 0 \\ x (x^{2} - 3 x + 2) & = 0 \\ x (x - 2) (x - 1) & = 0 \end{aligned}

::x3 - 3x2+2x=0x(x2 - 3x+2)=0x(x-2)(x-1)=0

The zeros are at $\begin{aligned} x = 0, x = 1, \end{aligned}$ and $\begin{aligned} x = 2 \end{aligned}$ .
::零是 x=0,x=1,和 x=2。

Interval	Test Point	Positive/Negative?	Part of Solution Set?
$\begin{aligned} (- \infty, 0) \end{aligned}$	-5	-	no
(0, 1)	$\begin{aligned} \frac{1}{2} \end{aligned}$	+	yes
(1, 2)	$\begin{aligned} \frac{3}{2} \end{aligned}$	-	no
$\begin{aligned} (2, + \infty) \end{aligned}$	3	+	yes

Notice that this inequality is greater than or equal to zero, so we include the zeros in the solution set . Therefore the solutions are $\begin{aligned} x \in [0, 1] \cup [2, + \infty] \end{aligned}$ .
::请注意,这种不平等大于或等于零,所以我们把零点包括在设定的解决方案中。因此,解决方案是 x[0,1] [2,]。

Example 3
::例3

Solve $\begin{aligned} 6 x^{4} + 5 x^{2} < 25 \end{aligned}$ .
::解决 6x4+5x2<25。

First we will change the inequality to $\begin{aligned} 6 x^{4} + 5 x^{2} - 25 < 0 \end{aligned}$ . Now, solve the equation $\begin{aligned} 6 x^{4} + 5 x^{2} - 25 = 0 \end{aligned}$ .
::首先,我们将把不平等性改变为 6x4+5x2 - 25 < 0。现在, 解析 6x4+5x2 - 25=0 方程式。

\begin{aligned} 6 x^{4} + 5 x^{2} - 25 & = 0 \\ (3 x^{2} - 5) (2 x^{2} + 5) & = 0 \end{aligned}

::6x4+5x2-25=0(3x2-5)(2x2+5)=0

The first term yields the solutions $\begin{aligned} x = \pm \sqrt{\frac{5}{3}} \end{aligned}$ and there are no real solutions for the second term.
::第一个术语产生解决方案 x53,第二个术语没有真正的解决方案。

Interval	Test Point	Positive/Negative?	Part of Solution Set?
$\begin{aligned} (- \infty, - \sqrt{\frac{5}{3}}) \end{aligned}$	-3	+	no
$\begin{aligned} (- \sqrt{\frac{5}{3}}, \sqrt{\frac{5}{3}}) \end{aligned}$	0	-	yes
$\begin{aligned} (\sqrt{\frac{5}{3}}, + \infty) \end{aligned}$	3	+	no

Finally, the solution set is $\begin{aligned} x \in (- \sqrt{\frac{5}{3}}, \sqrt{\frac{5}{3}}) \end{aligned}$ .
::最后,一套解决办法是x(-53,53)。

Example 4
::例4

Find the solution set of the inequality
::寻找不平等的一套解决办法

\begin{aligned} \frac{4 x - 12}{3 x - 2} < 0 \end{aligned}

::4 - 123x-2 < 0

From the numerator we solve $\begin{aligned} 4 x - 12 = 0 \end{aligned}$ or $\begin{aligned} x = 3 \end{aligned}$ . In the denominator, solve $\begin{aligned} 3 x - 2 = 0 \end{aligned}$ and we find the critical point $\begin{aligned} x = \frac{2}{3} \end{aligned}$ .
::我们从分子中解析 4x- 12= 0 或 x= 3。在分母中, 解析 3x-2= 0 并找到关键点 x= 23 。

Making the table
::安排会议桌

Interval	Test Point	Positive/Negative?	Part of Solution Set?
$\begin{aligned} (- \infty, \frac{2}{3}) \end{aligned}$	0	+	no
$\begin{aligned} (\frac{2}{3}, 3) \end{aligned}$	1	-	yes
$\begin{aligned} (3, + \infty) \end{aligned}$	5	+	no

Therefore, the solution set includes the numbers in the interval $\begin{aligned} (\frac{2}{3}, 3) \end{aligned}$ . Or in set-builder notation, the solution is $\begin{aligned} {x | \frac{2}{3} < x < 3} \end{aligned}$ .
::因此,所设定的解决方案包括间隔(23,3)中的数字,或者在设置-构建符符号中,解决方案是 {x23 <x<3}。

Example 5
::例5

(using technology) The McNeil Surf Company makes wetsuits. For a given number of wetsuits $\begin{aligned} x \end{aligned}$ , McNeil's profit, in dollars, is given by the function $\begin{aligned} P (x) = - 0.01 x^{2} + 25 x - 3000 \end{aligned}$ .
::McNeil Surf公司制造湿衣服。对于一定数量的湿衣服 x,McNeil的利润(美元)由函数P(x)0.01x2+25x-3000提供。

If the manager of McNeil wants the profit to stay above $9,000, what is the minimum and maximum number of wetsuits they can manufacture to maintain that level of profit?
::如果McNeil的经理希望利润维持在9 000美元以上,那么他们为保持这一利润水平可以制造的湿衣的最低和最高数量是多少?

Set up the inequality

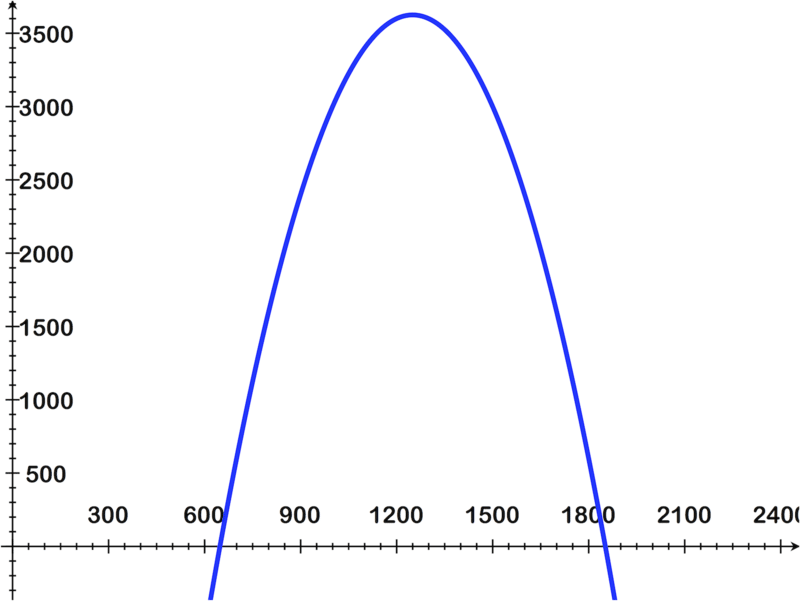
\begin{aligned} - 0.01 x^{2} + 25 x - 3000 & > 9000 \\ - 0.01 x^{2} + 25 x - 12000 & > 0 \end{aligned}

::设置不平等- 0.01x2+25x-3000>900- 0.01x2+25x-12000>0

With a calculator you can graph the function $\begin{aligned} Y_{1} = - 0.01 x^{2} + 25 x - 12000 \end{aligned}$ .
::您可以用计算器绘制函数 Y1\\ 0.01x2+25x- 12000 。

On a TI-83: use the window $\begin{aligned} [- 1000, 4000] \times [- 5000, 15000] \end{aligned}$ .
::在TI-83上:使用窗口[-1000,400]x[-500,150,000]。

The settings are:
::设置是:

$\begin{aligned} X m i n = - 1000, X m a x = 4000, X s c l = 500 \end{aligned}$
::Xmin1000,Xmax=400,Xscl=500

$\begin{aligned} Y m i n = - 5000, Y m a x = 5000, Y s c l = 1000 x r e s = 1 \end{aligned}$
::Ymin500,Ymax=500,Yscl=1000 xres=1

On a software grapher, the image looks like this with the window $\begin{aligned} x : 0 \to 2400 \end{aligned}$ and $\begin{aligned} y : 0 \to 3500 \end{aligned}$
::在软件图形仪上, 图像看起来像这样, 窗口 x: 0 2400 和 y: 0 3500 。

Using the CALC menu (2ND TRACE) , and selecting the option ZEROS , we can see that the zeros of $\begin{aligned} Y_{1} = - 0.01 x^{2} + 25 x - 12000 \end{aligned}$ are at $\begin{aligned} x = 647.920 \end{aligned}$ and $\begin{aligned} x = 1852.080 \end{aligned}$ .
::使用 CALC 菜单 (2ND TRACE) , 并选择选项 ZEROS, 我们可以看到, Y1 = 0.01x2+25x-12000 的零是 x= 647. 920 和 x= 18520.080 。

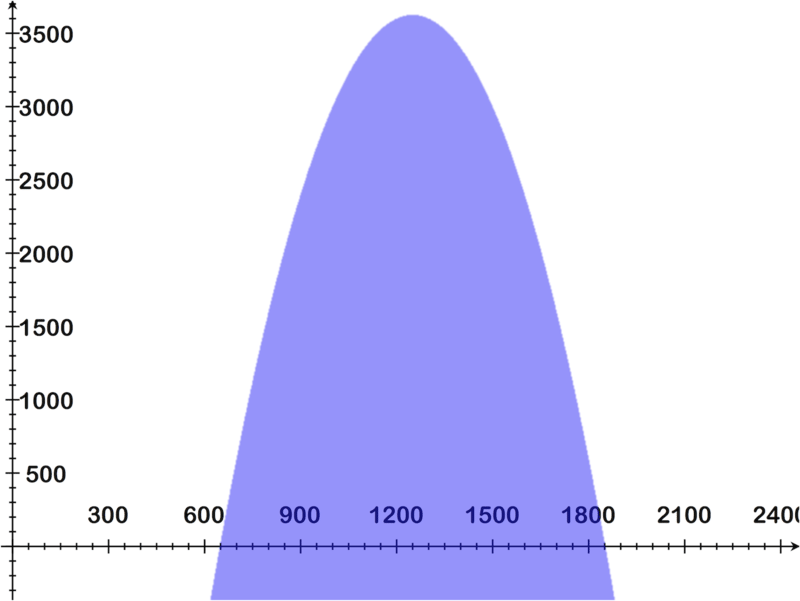
By inspecting the graph, we can see that the solution set to the inequality $\begin{aligned} - 0.01 x^{2} + 25 x - 12000 > 0 \end{aligned}$ is $\begin{aligned} x \in (648, 1852) \end{aligned}$ .
::通过查看图表,我们可以看到,解决不平等-0.01x2+25x-12000>0的解决方案是x(648,1852)。

Visually that looks like:
::直观地看似:

What is the maximum profit McNeil can make?
::McNeil能赚到的最大利润是什么?

Keeping the same graph open, use CALC MAXIMUM to solve for the maximum profit. The maximum is at (1250, 3625), indicating that the maximum profit is $3625 above the minimum we set: of $9000.
::使用 CALC MAXIMUM 解决最大利润。上限为 ( 1250, 3625 ) , 表示最大利润比我们设定的最低利润( 9 000 美元) 高出 3 625 美元。

So the actual maximum profit is $12,625 when 1250 wetsuits are produced.
::实际最大利润是12 625美元当1 250件湿衣生产时

Can you explain why this shape might make sense for a profit function?
::你能解释为什么这个形状对盈利功能有意义吗?

One possible reason the profit function might take this shape is labor costs. If McNeil wants to make a very large number of wetsuits in a short period of time, then that may require paying overtime for workers, and this could reduce the profit margin.
::盈利功能可能采取这种形式的原因之一是劳动成本。如果麦克尼尔希望在短短的时间内做大量湿衣,那么这可能需要为工人支付加班费,这可能会降低利润率。

Example 6
::例6

For the following rational function, determine limitations on the domain and the asymptotes, and then sketch the graph.
::对于以下的理性函数, 确定域和小元素的限制, 然后绘制图形。

$\begin{aligned} f (x) \geq \frac{2 x + 5}{x - 1} \end{aligned}$
:xx)2x+5x-1

To identify the graph of the inequality $\begin{aligned} f (x) \geq \frac{2 x + 5}{x - 1} \end{aligned}$ , first treat it as if it were the equality $\begin{aligned} f (x) \geq \frac{2 x + 5}{x - 1} \end{aligned}$
::为了确定不平等的图表 f(x)2x+5x-1, 先把它当做是平等 f(x)2x+5x-1

For $\begin{aligned} f (x) \geq \frac{2 x + 5}{x - 1} : \end{aligned}$
::f( x)% 2x+5x- 1 :

To find the critical points, identify the value(s) which make the denominator = 0: $\begin{aligned} x \neq 1 \end{aligned}$
::要找到临界点,请标明使分母 = 0: x1 的值

That gives us a vertical asymptote of $\begin{aligned} x = 1 \end{aligned}$
::给我们一个 x=1 的垂直空点

The horizontal asymptote becomes apparent as x becomes truly huge and the "+5" and "-1" no longer matter. At that point, we have $\begin{aligned} f (x) = \frac{2 x}{x} \to f (x) = 2 \end{aligned}$ So the horizontal asymptote is $\begin{aligned} y = 2 \end{aligned}$
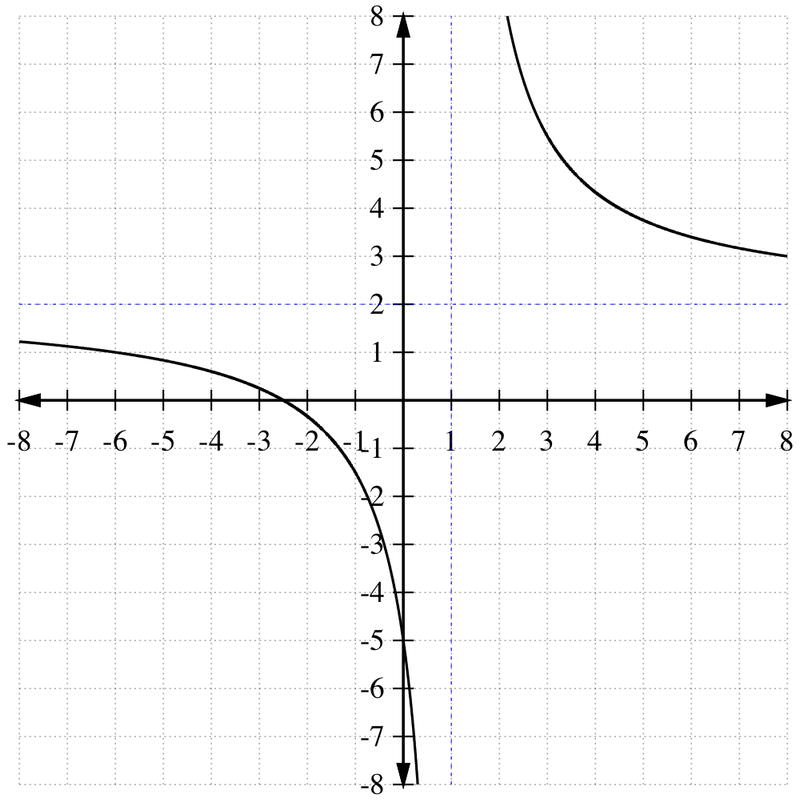
::随着 x 变得真正巨大, “ +5” 和“ 1” 不再重要, 水平末位变得显而易见。到那个时候, 我们有 f( x) = 2xxxf( x) =2, 所以水平末位是 y=2

Now that you know the shape of the graph, simply shade the area above the lines, since the original function was f ( x ) is greater-than function, and leave the lines solid since it was a greater-than or equal to .
::既然您知道图形的形状, 只需对线条上方的区域进行阴影, 因为原函数是 f( x) 大于函数, 并且让线条坚固, 因为它大于或等于。

The final graph should look like:
::最后的图表应该看起来像:

Review
::回顾

Find the solution set of the following inequalities without using a calculator. Display the solution set on a number line.
::在不使用计算器的情况下找到以下不平等的解决方案集。在数字行上显示设定的解决方案集。

$\begin{aligned} x^{2} + 2 x - 3 \leq 0 \end{aligned}$
::x2+2x-30

$\begin{aligned} 3 x^{2} - 7 x + 2 > 0 \end{aligned}$
::3x2-7x+2>0

$\begin{aligned} - 6 x^{2} - 13 x + 5 \geq 0 \end{aligned}$
::- 6x2-13x+50

$\begin{aligned} \frac{5 x - 1}{x - 2} > 0 \end{aligned}$
::5-1x-2>0

$\begin{aligned} \frac{1 - x}{x} < 1 \end{aligned}$
::1 - xx < 1

Solve: $\begin{aligned} 4 x^{3} - 4 x^{2} - 3 x > 0 \end{aligned}$
::溶解: 4x3- 4x2- 3x>0

Solve: $\begin{aligned} \frac{x^{4}}{4} - x^{2} < 0 \end{aligned}$
::溶解: x44- x2 <0

Solve: $\begin{aligned} 4 x^{3} - 8 x^{2} - x + 2 \geq 0 \end{aligned}$
::溶解: 4x3- 8x2- x+2x0

$\begin{aligned} \frac{n^{3} - 2 n^{2} - n + 2}{n^{3} + 3 n^{2} + 4 n + 12} < 0 \end{aligned}$
::n3-2n2-n+2n3+3n2+4n+12 <0

$\begin{aligned} \frac{n^{3} + 3 n^{2} - 4 n - 12}{n^{3} - 5 n^{2} + 4 n - 20} \leq 0 \end{aligned}$
::n3+3n2 - 4n - 12n3 - 5n2+4n - 200

$\begin{aligned} \frac{2 n^{3} + 5 n^{2} - 18 n - 45}{3 n^{3} - n^{2} + 27 n - 9} \geq 0 \end{aligned}$
::2n3+5n2-18n-453n3-n2+27n-90

$\begin{aligned} \frac{12 n^{3} + 16 n^{2} - 3 n - 4}{8 n^{3} + 12 n^{2} + 10 n + 15} > 0 \end{aligned}$
::12n3+16n2-3n-48n3+12n2+10n+15>0

Use a calculator to solve the following inequalities. Round your answer to three places after the decimal.
::使用计算器来解决以下的不平等。将您的答复四舍五入到小数点后的三个位。

$\begin{aligned} - 9.8 t^{2} + 357.6 t \geq 0 \end{aligned}$
::-9.8吨2+357.6吨0

$\begin{aligned} x^{3} - 5 x + 7 \leq - 4 x^{2} + 18 \end{aligned}$
::x3 - 5x+7\\\\\\\\\\\\\\2+18

$\begin{aligned} \frac{x^{2} - 2 x}{x - 5} > x^{2} - 25 \end{aligned}$
::x2-2xx-5>x2-2-25

Solve and graph: $\begin{aligned} f (x) > \frac{9 x^{2} - 4}{3 x + 2} \end{aligned}$
::溶解和图形: f( x) > 9x2 - 43x+2

The total resistance of two electronics components wired in parallel is given by $\begin{aligned} \frac{R_{1} R_{2}}{R_{1} + R_{2}} \end{aligned}$ where $\begin{aligned} R_{1} \end{aligned}$ and $\begin{aligned} R_{2} \end{aligned}$ are the individual resistances (in Ohms) of the two components. a) If the resistance of $\begin{aligned} R_{1} \end{aligned}$ is 20 Ohms, what is the maximum resistance of $\begin{aligned} R_{2} \end{aligned}$ if the total resistance must be less than 15 Ohms? b) What is the maximum theoretical resistance of this circuit? How do you know?
::R1R2R1+R2给出了平行连接的两个电子部件的总抗药性,R1和R2是这两个部件的个人抗药性。 a)如果R1的抗药性为20奥姆,如果总抗药性必须小于15奥姆,R2的最大抗药性是什么?b)这个电路最大的理论抗药性是什么?你怎么知道?

A rectangular lot of land has a length that is 7 meters more than twice its width. If the area of the lot is greater than 60 square meters, what are the possible values of the widths of the lot?
::长方形土地的长度为7米,是其宽度的两倍以上。如果其面积大于60平方米,那么其宽度的可能值是多少?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

多元和理性不平等

Polynomial and Rational Inequalities ::多元和理性不平等

Polynomial Inequalities ::多元不平等

Rational Inequalities ::理性不平等

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)