Course: 10.1 原产物带有Vertex的Parabolas

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 原产地带有Vetex的帕拉布拉斯

Collapse Expand
原产地带有Vetex的帕拉布拉斯
The area of a square is represented by the equation $\begin{aligned} y = 9 x^{2} \end{aligned}$ . What are the focus and directrix of this equation?
::公式y=9x2表示方形的区域。这个方形的重点和准点是什么?

Parabolas with Vertex at the Origin
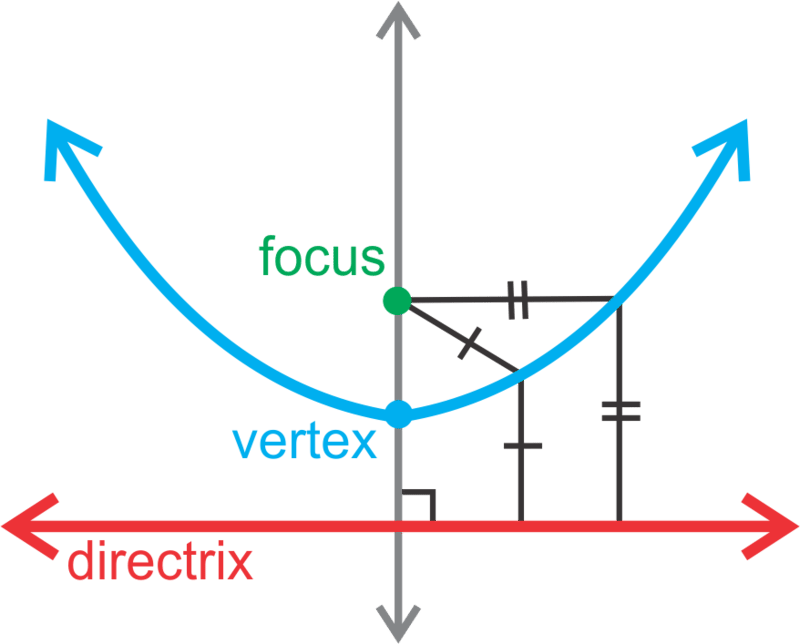
::原产地带有Vetex的帕拉布拉斯

You already know that the graph of a parabola has the parent graph $\begin{aligned} y = x^{2} \end{aligned}$ , with a vertex of $\begin{aligned} (0, 0) \end{aligned}$ and an axis of of $\begin{aligned} x = 0 \end{aligned}$ . A parabola can also be defined in a different way. It has a property such that any point on it is equidistant from another point, called the focus , and a line called the directrix .
::您已经知道, 抛物线的图形有父形图 y=x2, 其顶点为 0, 轴为 x=0。抛物线也可以以不同的方式定义。它的属性是, 它的任何点从另一个点, 称为焦点, 和直线, 其上的任何点都相等。

The focus is on the axis of symmetry and the vertex is halfway between it and the directrix. The directrix is perpendicular to the axis of symmetry.
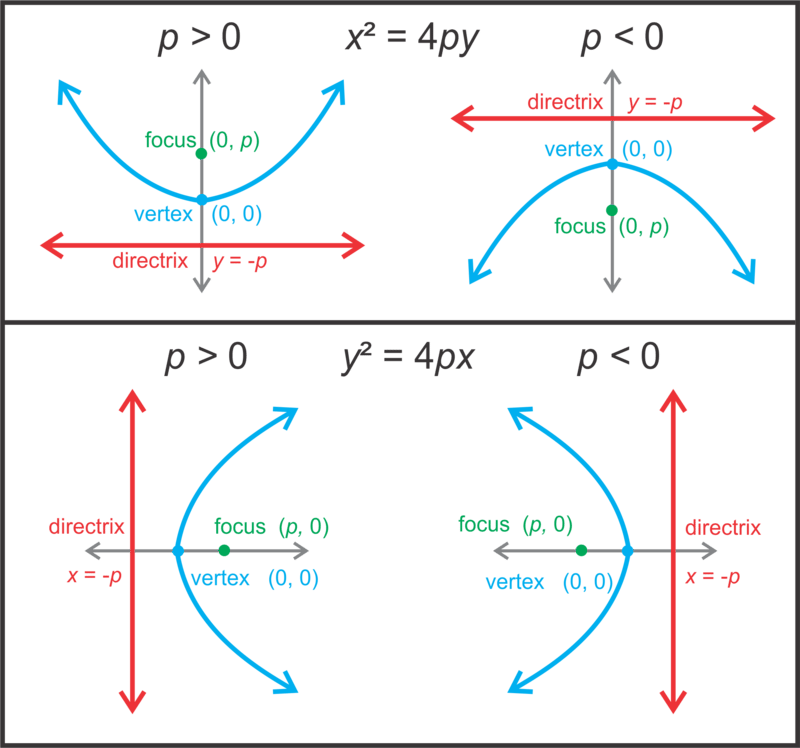
::焦点在对称轴上, 顶端介于对称轴与对称轴之间。直径与对称轴垂直。

Until now, we have been used to seeing the equation of a parabola like $\begin{aligned} y = a x^{2} \end{aligned}$ . In this concept, we will rewrite the equation to look like $\begin{aligned} x^{2} = 4 p y \end{aligned}$ where $\begin{aligned} p \end{aligned}$ is used to find the focus and directrix. We will also draw the parabola with a horizontal orientation, such that the equation will be $\begin{aligned} y^{2} = 4 p x \end{aligned}$ .
::到目前为止,我们已经习惯于看到象 y=ax2 这样的抛物线的方程。在这个概念中, 我们将重写方程, 以看起来像 x2= 4py , p 用来查找焦点和指针。我们还会绘制横向方向的抛物线, 这样方程将会是 y2= 4px 。

Notice, that when the parabola opens to the left or right, the $\begin{aligned} y \end{aligned}$ is squared. In this concept, the vertex will be $\begin{aligned} (0, 0) \end{aligned}$ .
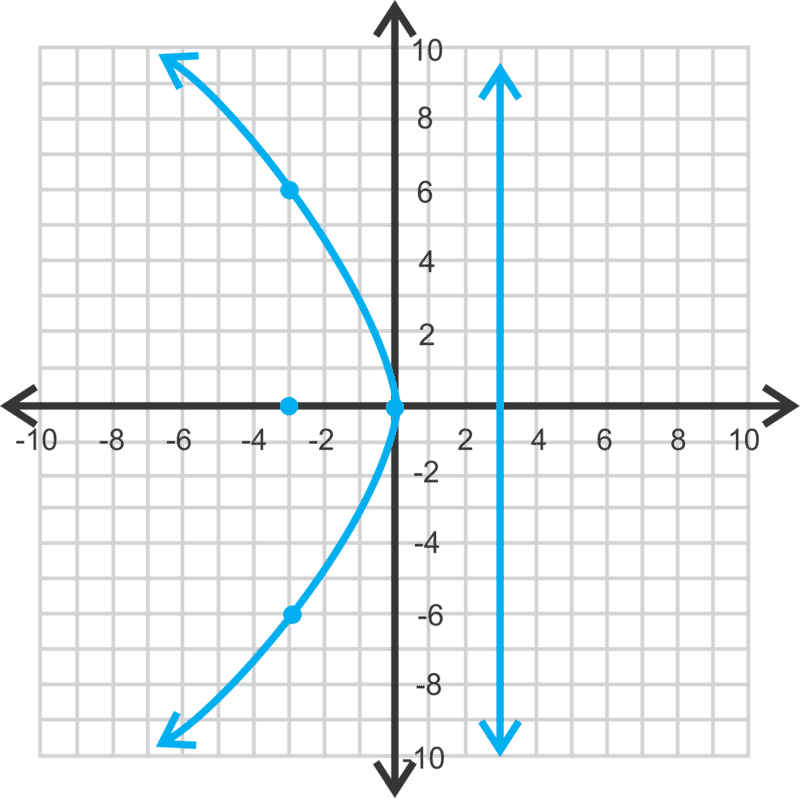
::注意, 当抛物线向左或向右打开时, y 是正方形。在这个概念中, 顶点将是 0,0 。

Let's analyze the equation $\begin{aligned} y^{2} = - 12 x \end{aligned}$ . We'll find the focus, directrix, and determine if the function opens up, down, to the left or right. Then, we'll graph the parabola.
::让我们分析一下 y2\\\ 12x 的方程。我们会找到焦点, 指针, 并确定函数是否向上、向下、向左或向右打开。然后, 我们会绘制抛物线。

To find the focus and directrix, we need to find $\begin{aligned} p \end{aligned}$ . We can set $\begin{aligned} - 12 = 4 p \end{aligned}$ and solve for $\begin{aligned} p \end{aligned}$ .
::为了找到焦点和主轴,我们需要找到p。我们可以设置 - 12=4p 并解决p。

$\begin{aligned} - 12 & = 4 p \\ - 3 & = p \end{aligned}$

::- 12=4p-3=p

Because $\begin{aligned} y \end{aligned}$ is squared, we know that the parabola opens to the left or right. Because $\begin{aligned} p \end{aligned}$ is negative, we know it is going to open to the left, towards the negative side of the $\begin{aligned} x \end{aligned}$ -axis. Using the pictures above, this parabola is like the second one under $\begin{aligned} y^{2} = 4 p x \end{aligned}$ . Therefore, the focus is $\begin{aligned} (- 3, 0) \end{aligned}$ and the directrix is $\begin{aligned} x = 3 \end{aligned}$ . To graph the parabola, plot the vertex, focus, directrix, and sketch the curve. Find at least one or two points on the curve to make sure your sketch is accurate. For example, because $\begin{aligned} (- 3, 6) \end{aligned}$ is on the parabola, then $\begin{aligned} (- 3, - 6) \end{aligned}$ is also on the parabola because it is symmetrical.
::因为 y 是正方, 我们知道 parbola 向左或右打开。因为 p 是负的, 我们知道它会向左打开, 向 x 轴的负面打开。使用上面的图片, 这个 parbola 和 y2 = 4px 下的第二个相似。因此, 焦点是 (- 3, 0) , 直线是 x = 3 。绘制 parbola 的图示, 绘制 parbola 、 verex、焦点、直线和画出曲线。在曲线上至少找到一两个点, 以确保您的草图准确。例如, 因为 (- 3, 6) 在 parbola 上, 那么 (- 3 - 6) 也位于 parbola 上, 因为它是对称的。

Notice that the points $\begin{aligned} (- 3, 6) \end{aligned}$ and $\begin{aligned} (- 3, - 6) \end{aligned}$ are equidistant from the focus and the directrix. They are both 6 units from each.
::注意要点(-3、6)和要点(-3、6)与重点和准点的距离相当,每个点各有6个单位。

The focus of a parabola is $\begin{aligned} (0, \frac{1}{2}) \end{aligned}$ . Let's find the equation of the parabola.
::抛物线的焦点是(0,12),让我们找到抛物线的方程。

Because the $\begin{aligned} p \end{aligned}$ value is the $\begin{aligned} y \end{aligned}$ -value and positive, this parabola is going to open up. So, the general equation is $\begin{aligned} x^{2} = 4 p y \end{aligned}$ . Plugging in $\begin{aligned} \frac{1}{2} \end{aligned}$ for $\begin{aligned} p \end{aligned}$ , we have $\begin{aligned} x^{2} = 4 \cdot \frac{1}{2} y \end{aligned}$ or $\begin{aligned} x^{2} = 2 y \end{aligned}$ .
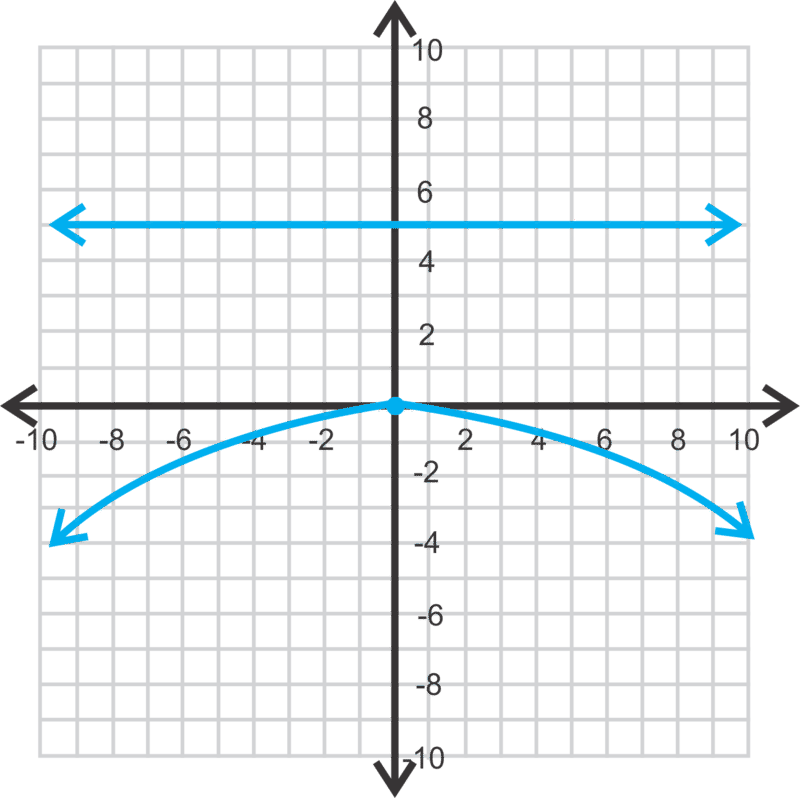
::因为 p 值是 Y 值和正值, 此抛物线将会打开。因此, 普通方程是 x2=4py 。 p 的插件在 12 中, 我们有 x2= 412y 或 x2=2y 。

Now, let's find the equation of the parabola below.
::现在,让我们来看看下面的抛物线方程式的方程式

The equation of the directrix is $\begin{aligned} y = 5 \end{aligned}$ , which means that $\begin{aligned} p = - 5 \end{aligned}$ and the general equation will be $\begin{aligned} x^{2} = 4 p y \end{aligned}$ . Plugging in -5 for $\begin{aligned} p \end{aligned}$ , we have $\begin{aligned} x^{2} = - 20 y \end{aligned}$ .
::直线的方程是 Y= 5, 这意味着 p5 和一般方程将是 x2= 4py。 p 插进 - 5, 我们有 x2\\ 20y 。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the focus and directrix of the equation $\begin{aligned} y = 9 x^{2} \end{aligned}$ .
::早些时候,有人要求你找到y=9x2方程式的焦点和准点。

To find the focus and directrix, we need to solve for $\begin{aligned} x^{2} \end{aligned}$ and then find $\begin{aligned} p \end{aligned}$ .
::要找到焦点和指针我们需要解决x2 然后找到p

$\begin{aligned} y = 9 x^{2} \\ \frac{1}{9} y = x^{2} \end{aligned}$

::y= 9x219y=x2

We can now set $\begin{aligned} \frac{1}{9} = 4 p \end{aligned}$ and solve for $\begin{aligned} p \end{aligned}$ .
::我们现在可以设定 19=4p 并解决p。

$\begin{aligned} \frac{1}{9} = 4 p \\ \frac{1}{36} = p \end{aligned}$

::19=4p136=p

Therefore, the focus is $\begin{aligned} (0, \frac{1}{36}) \end{aligned}$ and the directrix is $\begin{aligned} y = - \frac{1}{36} \end{aligned}$ .
::因此,焦点是(0,136),主轴是Y136。

Example 2
::例2

Determine if the parabola $\begin{aligned} x^{2} = - 2 y \end{aligned}$ opens up, down, left or right.
::确定抛物线 x2\%2y 是否向上、向下、向左或向右打开。

Down; $\begin{aligned} p \end{aligned}$ is negative and $\begin{aligned} x \end{aligned}$ is squared.
::向下;p为负,x为平方。

Example 3
::例3

Find the focus and directrix of $\begin{aligned} y^{2} = 6 x \end{aligned}$ . Then, graph the parabola.
::查找 y2=6x 的焦点和指向。然后,请绘制抛物线。

Solving for $\begin{aligned} p \end{aligned}$ , we have $\begin{aligned} 4 p = 6 \to p = \frac{3}{2} \end{aligned}$ . Because $\begin{aligned} y \end{aligned}$ is squared and $\begin{aligned} p \end{aligned}$ is positive, the parabola will open to the right. The focus is $\begin{aligned} (\frac{3}{2}, 0) \end{aligned}$ and the directrix is $\begin{aligned} x = - \frac{3}{2} \end{aligned}$ .
::解决 p, 我们有 4p= 6p= 32。因为 y 正方和正方, 抛物线会向右打开。焦点是 (32, 0) , 直线是 x32 。

Example 4
::例4

Find the equation of the parabola with directrix $\begin{aligned} x = - \frac{3}{8} \end{aligned}$ .
::找到有直线的抛物线方程式 x38。

If the directrix is negative and vertical $\begin{aligned} (x =) \end{aligned}$ , we know that the equation is going to be $\begin{aligned} y^{2} = 4 p x \end{aligned}$ and the parabola will open to the right, making $\begin{aligned} p \end{aligned}$ positive; $\begin{aligned} p = \frac{3}{8} \end{aligned}$ . Therefore, the equation will be $\begin{aligned} y^{2} = 4 \cdot \frac{3}{8} \cdot x \to y^{2} = \frac{3}{2} x \end{aligned}$ .
::如果直径为负和垂直(x=),我们知道方程将为y2=4px,而抛物线向右打开,使p正;p=38。因此,方程将为y2=438xy2=32x。

Review
::回顾

Determine if the parabola opens to the left, right, up or down.
::确定抛物线是否向左、右、上或下打开。

$\begin{aligned} x^{2} = 4 y \end{aligned}$
::x2=4y

$\begin{aligned} y^{2} = - \frac{1}{2} x \end{aligned}$
::y212x

$\begin{aligned} x^{2} = - y \end{aligned}$
::x2 y

Find the focus and directrix of the following parabolas.
::找到以下抛物线的焦点和准点。

$\begin{aligned} x^{2} = - 2 y \end{aligned}$
::x2 2y

$\begin{aligned} y^{2} = \frac{1}{4} x \end{aligned}$
::y2=14x y2=14x

$\begin{aligned} y^{2} = - 5 x \end{aligned}$
::y25x

Graph the following parabolas. Identify the focus and directrix as well.
::如下图所示,还标明重点和主轴。

$\begin{aligned} x^{2} = 8 y \end{aligned}$
::x2=8y

$\begin{aligned} y^{2} = \frac{1}{2} x \end{aligned}$
::y2=12x y2=12x

$\begin{aligned} x^{2} = - 3 y \end{aligned}$
::x2 3y

Find the equation of the parabola given that the vertex is $\begin{aligned} (0, 0) \end{aligned}$ and the focus or directrix.
::查找抛物线的方程,因为顶点是(0,0)和焦点或直线。

focus: $\begin{aligned} (4, 0) \end{aligned}$
::重点: (4,0)

directrix: $\begin{aligned} x = 10 \end{aligned}$
::直径: x=10

focus: $\begin{aligned} (0, \frac{7}{2}) \end{aligned}$
::重点: (0,72)

You have seen that earlier the basic parabolic equation was $\begin{aligned} y = a x^{2} \end{aligned}$ . Now, we write $\begin{aligned} x^{2} = 4 p y \end{aligned}$ . Rewrite $\begin{aligned} p \end{aligned}$ in terms of $\begin{aligned} a \end{aligned}$ and determine how they affect each other.
::您已经看到,早些时候的基本抛物线方程是 y= ax2。现在, 我们以 a 写 x2= 4py。重写 p , 并确定它们相互的影响。

Challenge Use the distance formula, $\begin{aligned} d = \sqrt{{(x_{2} - x_{1})}^{2} - {(y_{2} - y_{1})}^{2}} \end{aligned}$ , to prove that the point $\begin{aligned} (4, 2) \end{aligned}$ is on the parabola $\begin{aligned} x^{2} = 8 y \end{aligned}$ .
::挑战使用距离公式 d=(x2-x1)2-(y2-y1)2,以证明点(4,2)在抛物线x2=8y上。

Real World Application A satellite dish is a 3-dimensional parabola used to retrieve sound, TV, or other waves. Assuming the vertex is $\begin{aligned} (0, 0) \end{aligned}$ , where would the focus have to be on a satellite dish that is 4 feet wide and 9 inches deep? You may assume the parabola has a vertical orientation (opens up).
::真实世界应用程序 A 卫星天线是用于检索声音、电视或其他波浪的三维抛物线。假设顶点是 0,0 , 重点应该放在宽4英尺、深9英寸的卫星天线上? 您可以假设抛物线有一个垂直方向( 打开) 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

原产地带有Vetex的帕拉布拉斯

Parabolas with Vertex at the Origin ::原产地带有Vetex的帕拉布拉斯

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Parabolas with Vertex at the Origin
::原产地带有Vetex的帕拉布拉斯

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)