课程： 10.6 以 (h, k) 居于(h, k) 处的椭圆

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

以 (h, k) 居于(h, k) 的椭圆

Your homework assignment is to draw the ellipse $\begin{aligned} 16 (x - 2)^{2} + 4 (y + 3)^{2} = 144 \end{aligned}$ . What is the vertex of your graph and where will the foci of the ellipse be located?
::您的作业任务是绘制 16 (x-2) 2,2+4(y+3)2=144 。您的图表的顶点是什么? 椭圆的顶点在哪里?

Ellipses Centered at (h,k)
::位于 (h,k) 的椭圆

An ellipse does not always have to be placed with its center at the origin. If the center is $\begin{aligned} (h, k) \end{aligned}$ the entire ellipse will be shifted $\begin{aligned} h \end{aligned}$ units to the left or right and $\begin{aligned} k \end{aligned}$ units up or down. The equation becomes $\begin{aligned} \frac{{(x - h)}^{2}}{a^{2}} + \frac{{(y - k)}^{2}}{b^{2}} = 1 \end{aligned}$ . We will address how the vertices, co-vertices, and foci change in the following problem.
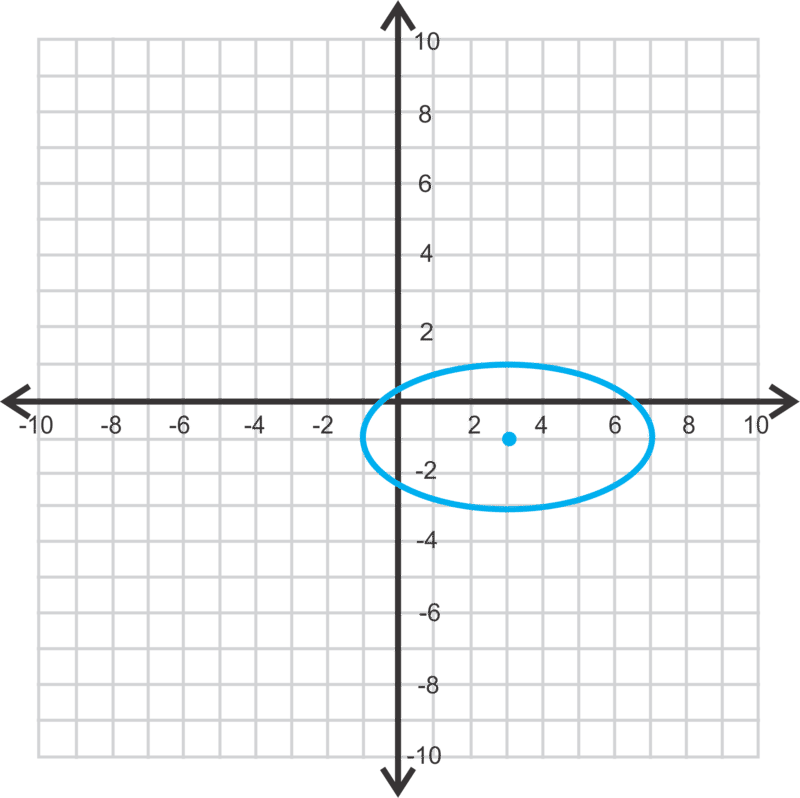
::椭圆不一定总是以其中心位于源头。如果中心是 (h, k) , 整个椭圆将被移动 h 单位到左边或右边, k 单位向上或向下。等式会变成 (x-h) 2a2+(y-k) 2b2=1. 。我们将处理以下问题的顶端、共垂直和角变化。

Let's graph $\begin{aligned} \frac{{(x - 3)}^{2}}{16} + \frac{{(y + 1)}^{2}}{4} = 1 \end{aligned}$ . Then, we'll find the vertices, co-vertices, and foci.
::让我们绘制图表( x-33) 216+(y+1)24=1。然后,我们会找到顶点、共同的顶点和顶点。

First, we know this is a horizontal ellipse because $\begin{aligned} 16 > 4 \end{aligned}$ . Therefore, the center is $\begin{aligned} (3, - 1) \end{aligned}$ and $\begin{aligned} a = 4 \end{aligned}$ and $\begin{aligned} b = 2 \end{aligned}$ . Use this information to graph the ellipse.
::首先,我们知道这是一个水平椭圆, 因为 16> 4 。因此, 中心是 (3, ~ 1) 和 a= 4 和 b= 2 。使用此信息来绘制椭圆。

To graph, plot the center and then go out 4 units to the right and left and then up and down two units. This is also how you can find the vertices and co-vertices. The vertices are $\begin{aligned} (3 \pm 4, - 1) \end{aligned}$ or $\begin{aligned} (7, - 1) \end{aligned}$ and $\begin{aligned} (- 1, - 1) \end{aligned}$ . The co-vertices are $\begin{aligned} (3, - 1 \pm 2) \end{aligned}$ or $\begin{aligned} (3, 1) \end{aligned}$ and $\begin{aligned} (3, - 3) \end{aligned}$ .
::绘制图示,绘制中心,然后从4个单位向右和向左,然后向上和向下移动两个单位。这也是您如何找到顶部和共同的顶部。顶部是(3+4,-1)或(7,-1)或(7,-1)和(-1,-1)或(3,1)或(3,1)和(3,-3)。

To find the foci, we need to find $\begin{aligned} c \end{aligned}$ using $\begin{aligned} c^{2} = a^{2} - b^{2} \end{aligned}$ .
::要找到foci, 我们需要用 c2=a2 -b2 找到 c。

\begin{aligned} c^{2} & = 16 - 4 = 12 \\ c & = 2 \sqrt{3} \end{aligned}

::c2=16-4=12c=23

Therefore, the foci are $\begin{aligned} (3 \pm 2 \sqrt{3}, - 1) \end{aligned}$ .
::因此,核心是(323)-1。

From this problem, we can create formulas for finding the vertices, co-vertices, and foci of an ellipse with center $\begin{aligned} (h, k) \end{aligned}$ . Also, when graphing an ellipse, not centered at the origin, make sure to plot the center.
::从这个问题中,我们可以创建公式来寻找具有中枢(h,k)的椭圆的顶部、共同的顶部和顶部。此外,在绘制不是以原为中心、但并非以原为中心的椭圆的图形时,确保绘制中心。

Orientation	Equation	Vertices	Co-Vertices	Foci
Horizontal	$\begin{aligned} \frac{{(x - h)}^{2}}{a^{2}} + \frac{{(y - k)}^{2}}{b^{2}} = 1 \end{aligned}$	$\begin{aligned} (h \pm a, k) \end{aligned}$	$\begin{aligned} (h, k \pm b) \end{aligned}$	$\begin{aligned} (h \pm c, k) \end{aligned}$
Vertical	$\begin{aligned} \frac{{(x - h)}^{2}}{b^{2}} + \frac{{(y - k)}^{2}}{a^{2}} = 1 \end{aligned}$	$\begin{aligned} (h, k \pm a) \end{aligned}$	$\begin{aligned} (h \pm b, k) \end{aligned}$	$\begin{aligned} (h, k \pm c) \end{aligned}$

Now, let's find the equation of the ellipse with vertices $\begin{aligned} (- 3, 2) \end{aligned}$ and $\begin{aligned} (7, 2) \end{aligned}$ and co-vertex $\begin{aligned} (2, - 1) \end{aligned}$ .
::现在,让我们来看看椭圆的等式, 包括脊椎(-3,2)和(7,2), 和共脊(2,1-1)。

These two vertices create a horizontal major axis, making the ellipse horizontal. If you are unsure, plot the given information on a set of axes. To find the center, use the midpoint formula with the vertices.
::这两个顶点创建了水平主轴, 使椭圆水平。如果您不确定, 请在一组轴上绘制给定信息。要找到中心, 请使用顶点的中点公式。

$\begin{aligned} (\frac{- 3 + 7}{2}, \frac{2 + 2}{2}) = (\frac{4}{2}, \frac{4}{2}) = (2, 2) \end{aligned}$

The distance from one of the vertices to the center is $\begin{aligned} a \end{aligned}$ , $\begin{aligned} | 7 - 2 | = 5 \end{aligned}$ . The distance from the co-vertex to the center is $\begin{aligned} b \end{aligned}$ , $\begin{aligned} | - 1 - 2 | = 3 \end{aligned}$ . Therefore, the equation is $\begin{aligned} \frac{{(x - 2)}^{2}}{5^{2}} + \frac{{(y - 2)}^{2}}{3^{2}} = 1 \end{aligned}$ or $\begin{aligned} \frac{{(x - 2)}^{2}}{25} + \frac{{(y - 2)}^{2}}{9} = 1 \end{aligned}$ .
::从一个顶端到中间的距离是a, +7-25. 从共同顶端到中间的距离是b, +1-23. 因此, 方程是 (x-22)252+(y-2)232=1或 (x-2)225+(y-2)29=1。

Finally, let's graph $\begin{aligned} 49 (x - 5)^{2} + 25 (y + 2)^{2} = 1225 \end{aligned}$ and find the foci.
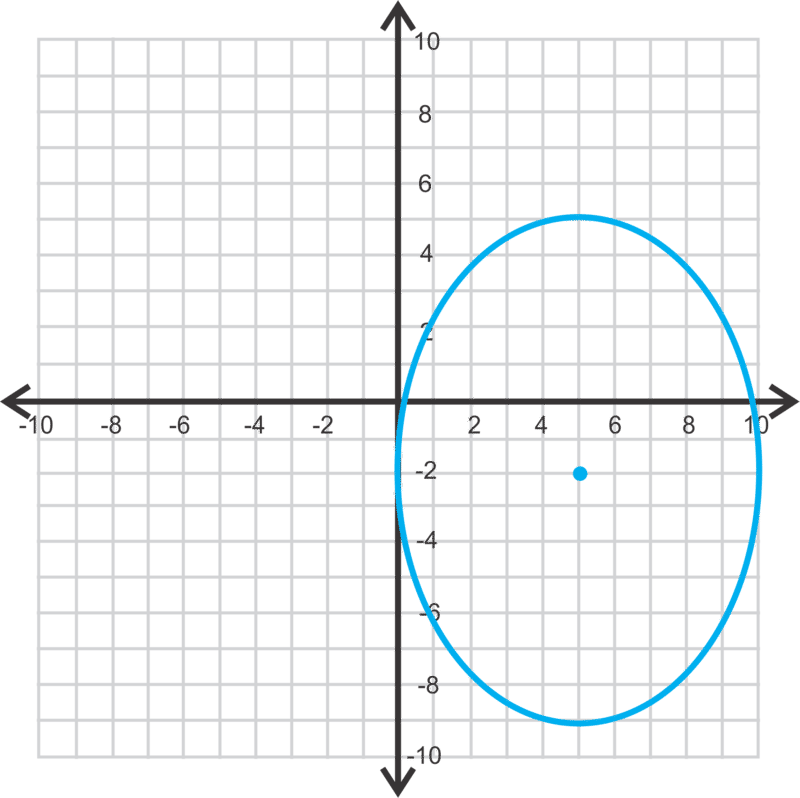
::最后,让我们看看图49(x-5)2+25(y+2)2=1225 并找到顶部。

First we have to get this into standard form, like the equations above. To make the right side 1, we need to divide everything by 1225.
::首先,我们必须把它变成标准的形式,像上面的方程式一样。为了右侧1,我们需要把所有东西除以1225。

\begin{aligned} \frac{49 {(x - 5)}^{2}}{1225} + \frac{25 {(y + 2)}^{2}}{1225} & = \frac{1225}{1225} \\ \frac{{(x - 5)}^{2}}{25} + \frac{{(y + 2)}^{2}}{49} & = 1 \end{aligned}

::49(x-5)21225+25(y+2)21225=12251225(x-55)225+(y+2)249=1

Now, we know that the ellipse will be vertical because $\begin{aligned} 25 < 49 \end{aligned}$ . $\begin{aligned} a = 7, b = 5 \end{aligned}$ and the center is $\begin{aligned} (5, - 2) \end{aligned}$ .
::我们知道椭圆是垂直的因为25<49. a=7,b=5,中心是5,2)

To find the foci, we first need to find $\begin{aligned} c \end{aligned}$ by using $\begin{aligned} c^{2} = a^{2} - b^{2} \end{aligned}$ .
::要找到角,我们首先需要通过使用 c2=a2 -b2 来找到 c。

\begin{aligned} c^{2} & = 49 - 25 = 24 \\ c & = \sqrt{24} = 2 \sqrt{6} \end{aligned}

::c2=49-25=24c=24=26

The foci are $\begin{aligned} (5, - 2 \pm 2 \sqrt{6}) \end{aligned}$ or $\begin{aligned} (5, - 6.9) \end{aligned}$ and $\begin{aligned} (5, 2.9) \end{aligned}$ .
::方块是(5,-226)或(5,-6.9)和(5,2.9)。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the vertex of your graph and to determine where the foci of the ellipse will be located.
::早些时候,有人要求你找到图表的顶端, 并确定椭圆的角的位置。

We first need to get our equation in the form of $\begin{aligned} \frac{{(x - h)}^{2}}{a^{2}} + \frac{{(y - k)}^{2}}{b^{2}} = 1 \end{aligned}$ . So we divide both sides by 144.
::我们首先需要以(x-h)2a2+(y-k)2b2=1的形式获得等式。因此,我们将双方除以144。

\begin{aligned} \frac{16 (x - 2)^{2}}{144} + \frac{4 (y + 3)^{2}}{144} = \frac{144}{144} \\ \frac{(x - 2)^{2}}{9} + \frac{(y + 3)^{2}}{36} \end{aligned}

::16(x-2-2)2144+4(y+3)2144=144144(x-2)29+(y+3)236

Now we can see that $\begin{aligned} h = 2 \end{aligned}$ and $\begin{aligned} 3 = - k \end{aligned}$ or $\begin{aligned} k = - 3 \end{aligned}$ . Therefore the origin is $\begin{aligned} (2, - 3) \end{aligned}$ .
::现在我们可以看到 h=2 和 3k 或 k3 。因此,起源于 (2, - 3) 。

Because $\begin{aligned} 9 < 36 \end{aligned}$ , we know this is a vertical ellipse. To find the foci, use $\begin{aligned} c^{2} = a^{2} - b^{2} \end{aligned}$ .
::因为9<36, 我们知道这是一个垂直的椭圆。要找到 foci, 请使用 c2=a2 - b2 。

\begin{aligned} c^{2} & = 36 - 9 = 27 \\ c & = \sqrt{27} = 3 \sqrt{3} \end{aligned}

::c2=36-9=27c=27=33

The foci are therefore $\begin{aligned} (2, - 3 + 3 \sqrt{3}) \end{aligned}$ and $\begin{aligned} (2, - 3 - 3 \sqrt{3}) \end{aligned}$ .
::因此,重点分别为(2,-3+33)和(2,-3-3-3-33)。

Example 2
::例2

Find the center, vertices, co-vertices and foci of $\begin{aligned} \frac{{(x + 4)}^{2}}{81} + \frac{{(y - 7)}^{2}}{16} = 1 \end{aligned}$ .
::查找 (x+4) 281+(y-7) 216=1 的中心、顶部、共同垂直和角。

The center is $\begin{aligned} (- 4, 7), a = \sqrt{81} = 9 \end{aligned}$ and $\begin{aligned} b = \sqrt{16} = 4 \end{aligned}$ , making the ellipse horizontal. The vertices are $\begin{aligned} (- 4 \pm 9, 7) \end{aligned}$ or $\begin{aligned} (- 13, 7) \end{aligned}$ and $\begin{aligned} (5, 7) \end{aligned}$ . The co-vertices are $\begin{aligned} (- 4, 7 \pm 4) \end{aligned}$ or $\begin{aligned} (- 4, 3) \end{aligned}$ and $\begin{aligned} (- 4, 11) \end{aligned}$ . Use $\begin{aligned} c^{2} = a^{2} - b^{2} \end{aligned}$ to find $\begin{aligned} c \end{aligned}$ .
::中心为(-4,7,a=81=9和b=16=4),使椭圆水平为水平。顶部为(-4,9,7)或(-13,7)和(-5,7),共同顶部为(-4,7,4)或(-4,3)和(-4,11),使用 c2=a2-b2来寻找c。

\begin{aligned} c^{2} & = 81 - 16 = 65 \\ c & = \sqrt{65} \end{aligned}

::c2=81-16=65c=65

The foci are $\begin{aligned} (- 4 - \sqrt{65}, 7) \end{aligned}$ and $\begin{aligned} (- 4 + \sqrt{65}, 7) \end{aligned}$ .
::核心是(-4-65,7)和(-4+65,7)。

Example 3
::例3

Graph $\begin{aligned} 25 (x - 3)^{2} + 4 (y - 1)^{2} = 100 \end{aligned}$ and find the foci.
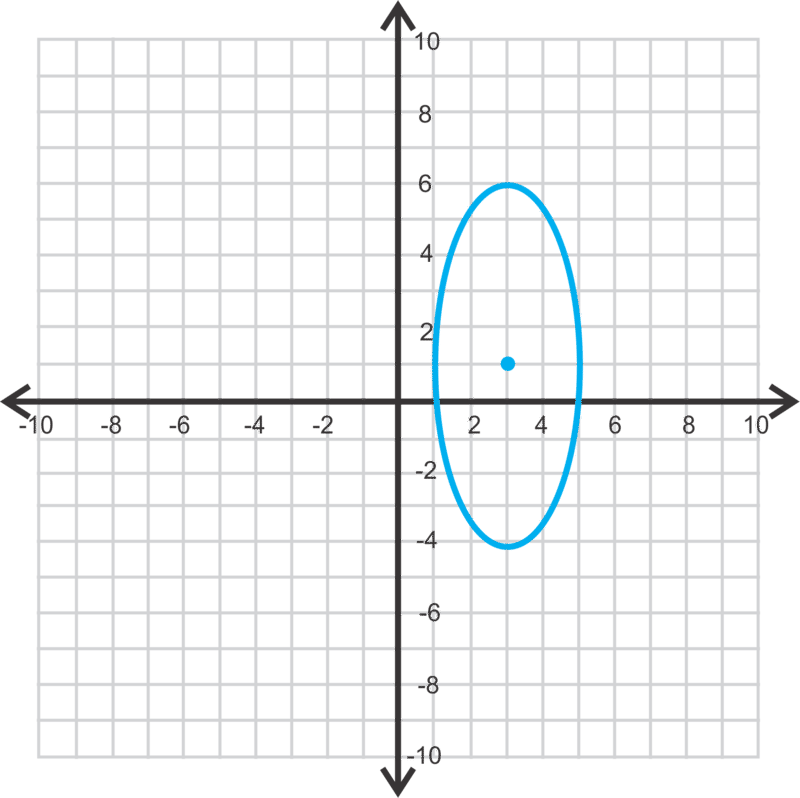
::图25(x-3)2+4(y-1)2=100并找到角。

Change this equation to standard form in order to graph.
::将此方程式更改为标准格式以图示。

\begin{aligned} \frac{25 {(x - 3)}^{2}}{100} + \frac{4 {(y - 1)}^{2}}{100} & = \frac{100}{100} \\ \frac{{(x - 3)}^{2}}{4} + \frac{{(y - 1)}^{2}}{25} & = 1 \end{aligned}

::25(x-3)2100+4(y-1)2100=100100(x-3)24+(y-1)225=1

center: $\begin{aligned} (3, 1), b = 2, a = 5 \end{aligned}$
::中间: (3, 1, b=2, a=5)

Find the foci.
::找到怪胎找到怪胎找到怪胎找到怪胎找到怪胎

\begin{aligned} c^{2} & = 25 - 4 = 21 \\ c & = \sqrt{21} \end{aligned}

::c2=25-4=21c=21

The foci are $\begin{aligned} (3, 1 + \sqrt{21}) \end{aligned}$ and $\begin{aligned} (3, 1 - \sqrt{21}) \end{aligned}$ .
::重点领域是(3,1+21)和(3,1+21)。

Example 4
::例4

Find the equation of the ellipse with co-vertices $\begin{aligned} (- 3, - 6) \end{aligned}$ and $\begin{aligned} (5, - 6) \end{aligned}$ and focus $\begin{aligned} (1, - 2) \end{aligned}$ .
::查找椭圆的等离子体和共白(-3,-6)和(-5,-6)的等离子体和焦点(1,-2)的等离子体。

The co-vertices $\begin{aligned} (- 3, - 6) \end{aligned}$ and $\begin{aligned} (5, - 6) \end{aligned}$ are the endpoints of the minor axis. It is $\begin{aligned} | - 3 - 5 | = 8 \end{aligned}$ units long, making $\begin{aligned} b = 4 \end{aligned}$ . The midpoint between the co-vertices is the center.
::共白(-3,-6)和(5,-6)是小轴的终点。是3+5+5+8 单位长,使 b=4。共白之间的中点是中点。

$\begin{aligned} (\frac{- 3 + 5}{2}, - 6) = (\frac{2}{2}, - 6) = (1, - 6) \end{aligned}$

The focus is $\begin{aligned} (1, - 2) \end{aligned}$ and the distance between it and the center is 4 units, or $\begin{aligned} c \end{aligned}$ . Find $\begin{aligned} a \end{aligned}$ .
::焦点是(1,-2),它与中心之间的距离是 4 个单位,或 c. 查找 a。

\begin{aligned} 16 & = a^{2} - 16 \\ 32 & = a^{2} \\ a & = \sqrt{32} = 4 \sqrt{2} \end{aligned}

::16=a2 - 1632=a2a=32=42

The equation of the ellipse is $\begin{aligned} \frac{{(x - 1)}^{2}}{16} + \frac{{(y + 6)}^{2}}{32} = 1 \end{aligned}$ .
::椭圆的方程式是 (x-1) 216+(y+6)232=1。

Review
::回顾

Find the center, vertices, co-vertices, and foci of each ellipse below.
::找到下方每个椭圆的中心、脊椎、共同的脊椎和角。

$\begin{aligned} \frac{{(x + 5)}^{2}}{25} + \frac{{(y + 1)}^{2}}{36} = 1 \end{aligned}$
:x+5)225+(y+1)236=1

$\begin{aligned} (x + 2)^{2} + 16 (y - 6)^{2} = 16 \end{aligned}$
:x+2)2+16(y-6)2=16

$\begin{aligned} \frac{{(x - 2)}^{2}}{9} + \frac{{(y - 3)}^{2}}{49} = 1 \end{aligned}$
:x-2)29+(y-3)249=1

$\begin{aligned} 25 x^{2} + 64 (y - 6)^{2} = 1600 \end{aligned}$
::25x2+64(y-6)2=1600

$\begin{aligned} (x - 8)^{2} + \frac{{(y - 4)}^{2}}{9} = 1 \end{aligned}$
:x-8)2+(y-4)29=1

$\begin{aligned} 81 (x + 4)^{2} + 4 (y + 5)^{2} = 324 \end{aligned}$
::81(x+4)2+4(y+5)2=324

Graph the ellipse in #1.
::在 # 1 中绘制椭圆图。

Graph the ellipse in #2.
::在 # 2 中绘制椭圆图。

Graph the ellipse in #4.
::在 # 4 中绘制椭圆图。

Graph the ellipse in #5.
::在 # 5 中绘制椭圆图。

Using the information below, find the equation of each ellipse.
::使用以下信息,找到每个椭圆的方程。

vertices: $\begin{aligned} (- 2, - 3) \end{aligned}$ and $\begin{aligned} (8, - 3) \end{aligned}$ co-vertex: $\begin{aligned} (3, - 5) \end{aligned}$
::顶点-2,-3)和(8,-3)共同顶点3,-5)

vertices: $\begin{aligned} (5, 6) \end{aligned}$ and $\begin{aligned} (5, - 12) \end{aligned}$ focus: $\begin{aligned} (5, - 7) \end{aligned}$
::脊椎5,6)和(5,12)重点5,7)

co-vertices: $\begin{aligned} (0, 4) \end{aligned}$ and $\begin{aligned} (14, 4) \end{aligned}$ focus: $\begin{aligned} (7, 1) \end{aligned}$
::共同垂直数: (0,4)和(14,4)重点: (7,1)

foci: $\begin{aligned} (- 11, - 4) \end{aligned}$ and $\begin{aligned} (1, - 4) \end{aligned}$ vertex: $\begin{aligned} (- 12, - 4) \end{aligned}$
::foci- 11,-4) 和(1,-4) 顶部- 12,-4)

Extension Rewrite the equation of the ellipse, $\begin{aligned} 36 x^{2} + 25 y^{2} - 72 x + 200 y - 464 = 0 \end{aligned}$ in standard form, by completing the square for both the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ terms.
::扩展名在标准格式中重写椭圆(36x2+25y2-72x+200y-464=0)的方程,填写方形时使用x和y两个词。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

以 (h, k) 居于(h, k) 的椭圆

Ellipses Centered at (h,k) ::位于 (h,k) 的椭圆

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)