Course: 10.8 撰写以原产地为中心的一个超博拉的等式

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 以起源为中心, 写作超波拉的等式

Collapse Expand
以起源为中心, 写作超波拉的等式
You are asked to solve a riddle. You are given the following pieces of information to help you.
::需要您解开谜题。您将获得以下信息来帮助您。

I am a centered at the origin.
::我是以起源为中心的人

My vertex is $\begin{align*}(0, -2)\end{align*}$ .
::我的顶部是( 0, - 2) 。

One of my foci is $\begin{align*}(0, -3)\end{align*}$ .
::我的一个要害是(0,-3)

What is my equation?
::我的方程式是什么?

The Equation of a Hyperbola
::超博拉之等式

In this concept, we are going to work backwards and find the equation of hyperbolas, given certain pieces of information. For this entire concept, the hyperbola will be centered at the origin.
::在这个概念中,我们将向后工作,找到超高波拉的方程式,给某些信息。对于这个整个概念,超波拉将以起源为中心。

Let's find the equation of the hyperbola, centered at the origin, with a vertex of $\begin{align*}(-4, 0)\end{align*}$ and focus of $\begin{align*}(-6, 0)\end{align*}$ .
::让我们找到双倍波拉的方程式, 以原点为中心, 顶点为( - 4, 0) 和焦点为( - 6, 0) 。

Because the vertex and focus are on the $\begin{align*}x\end{align*}$ -axis, we know that the transverse axis is horizontal. Therefore, the equation will be $\begin{align*}\frac{x^2}{a^2} - \frac{y^2}{b^2}=1\end{align*}$ . From the vertex, we know that $\begin{align*}a=4\end{align*}$ and $\begin{align*}c=6\end{align*}$ . Let’s solve for $\begin{align*}b^2\end{align*}$ using $\begin{align*}c^2=a^2+b^2\end{align*}$ .
::由于顶点和焦点在 x 轴上, 我们知道横轴是水平的。因此, 方程将是 x2a2 -y2b2=1. 从顶点上, 我们知道 a=4 和 c=6. 使用 c2=a2+b2 解决 b2 。

$\begin{aligned} 6^{2} & = 4^{2} + b^{2} \\ 36 & = 16 + b^{2} \to b^{2} = 20 \end{aligned}$
$\begin{align*}6^2 &= 4^2+b^2 \\ 36 &= 16+b^2 \rightarrow b^2=20\end{align*}$
::62=42+b236=16+b2=20

The equation of the hyperbola is $\begin{align*}\frac{x^2}{16} - \frac{y^2}{20}=1\end{align*}$ .
::双倍波拉的方程式是x216-y220=1。

Now, let's find the equation of the hyperbola, centered at the origin, with an asymptote of $\begin{align*}y=\frac{2}{3}x\end{align*}$ and vertex of $\begin{align*}(0, 12)\end{align*}$ .
::现在,让我们找到超博拉的方程, 以原点为中心, 以y=23x和顶点为 y=23x (0, 12) 的零点和顶点为中心。

We know that $\begin{align*}a=12\end{align*}$ , making the transverse axis is vertical and the general equation of the asymptote $\begin{align*}y=\frac{a}{b}x\end{align*}$ . Therefore, $\begin{align*}\frac{2}{3} = \frac{12}{b}\end{align*}$ , making $\begin{align*}b=18\end{align*}$ . Therefore, the equation of the hyperbola is $\begin{align*}\frac{y^2}{144} - \frac{x^2}{324}=1\end{align*}$ .
::我们知道,a=12, 横轴是垂直的, 和无ymptote y=abx的一般等式。因此, 23=12b, 使 b=18。因此, 超博拉的等式是 y2144 - x2324=1 。

In this problem, we showed that the slope of the asymptote can be reduced to something that is not always $\begin{align*}\frac{a}{b}\end{align*}$ , but $\begin{align*}c \left(\frac{m}{n}\right) = \frac{a}{b}\end{align*}$ , where $\begin{align*}c\end{align*}$ is some constant that we can reduce the fraction by.
::在这个问题上,我们表明,小行星的斜坡可以缩小为不总是 ab,而是 c(mn)=ab, c 是某种常数, 我们可以通过这些常数来减少小行星的分数。

Finally, let's find the equations of two hyperbolas with an asymptote of $\begin{align*}y= -\frac{5}{9}x\end{align*}$ .
::最后,让我们找到两个高音方程式的方程式, 加上一个y59x的零星状态。

This asymptote can be for either a vertical or horizontal hyperbola. $\begin{align*}-\frac{5}{9}\end{align*}$ can also be a reduced fraction of $\begin{align*}\frac{a}{b}\end{align*}$ , like in the previous problem . For example, the asymptote $\begin{align*}y=-\frac{10}{18}x\end{align*}$ reduces to $\begin{align*}y=-\frac{5}{9}x\end{align*}$ .
::可以是垂直的,也可以是水平的。 ~ 59 也可以是 ab 的缩小部分, 与前一个问题一样。例如, y { 1018x 的缩写会降低到 y 59x 。

If the hyperbola is horizontal, then the equation of the asymptote is $\begin{align*}y=-\frac{b}{a}x\end{align*}$ and that would make $\begin{align*}a=9\end{align*}$ and $\begin{align*}b=5\end{align*}$ and the equation would be $\begin{align*}\frac{x^2}{81} - \frac{y^2}{25}=1\end{align*}$ . If the equation is vertical, then the asymptote is $\begin{align*}y=-\frac{a}{b}x\end{align*}$ and $\begin{align*}a=5\end{align*}$ and $\begin{align*}b=9\end{align*}$ . The equation would be $\begin{align*}\frac{y^2}{25} - \frac{x^2}{81}=1\end{align*}$ . If the slope is reduced from a larger fraction, we could also have $\begin{align*}\frac{x^2}{324} - \frac{y^2}{100}=1\end{align*}$ or $\begin{align*}\frac{y^2}{100} - \frac{x^2}{324}=1\end{align*}$ as a possible answer.
::如果双波拉是水平的,那么时空方程式的方程式是 ybax, 这将使 a=9 和 b=5, 方程式是 x281 -y225=1. 如果方程式是垂直的, 则星际方程式是 yabx 和 a=5 和 b=9. 等式将是 y225 - x281=1. 如果斜度从较大部分缩小, 我们也可以将 x2324 -y2100=1 或 y2100 - x2324=1 作为可能的答案。

There are infinitely many hyperbolic equations with this asymptote.
::无限多的双曲方程式与这个无症状的方程式。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the equation of the parabola given the riddle.
::早些时候,你被要求从谜题中找到抛物线方程式的方程式

Because the vertex and focus are on the $\begin{align*}y\end{align*}$ -axis, we know that the transverse axis is vertical. Therefore, the equation will be $\begin{align*}\frac{y^2}{a^2} - \frac{x^2}{b^2}=1\end{align*}$ .
::因为顶点和焦点在 Y 轴上, 我们知道横轴是垂直的。因此, 方程式将是 y2a2- x2b2=1 。

From the vertex and the focus, we know that $\begin{align*}a=2\end{align*}$ and $\begin{align*}c=3\end{align*}$ . Let’s solve for $\begin{align*}b^2\end{align*}$ using $\begin{align*}c^2=a^2+b^2\end{align*}$ .
::从顶端和焦点, 我们知道 a=2 和 c=3。我们用 c2=a2+b2 解决 b2 。

$\begin{aligned} 3^{2} & = 2^{2} + b^{2} \\ 9 & = 4 + b^{2} \to b^{2} = 5 \end{aligned}$
$\begin{align*}3^2 &= 2^2+b^2 \\ 9 &= 4+b^2 \rightarrow b^2=5\end{align*}$
::32=22+b29=4+b2=5

Therefore, the equation of the hyperbola will be $\begin{align*}\frac{y^2}{4} - \frac{x^2}{5}=1\end{align*}$ .
::因此,双倍波拉的方程式将是y24-x25=1。

Find the equation of the following hyperbolas, centered at the origin, with the given information.
::用给定的信息查找以下双螺旋的方程, 以来源为中心。

Example 2
::例2

vertex: $\begin{align*}(0, 2)\end{align*}$
::顶点: (0, 2)

focus: $\begin{align*}(0, 5)\end{align*}$
::焦点: (0,5)

The vertex is on the $\begin{align*}y\end{align*}$ -axis, so this is a vertical hyperbola with $\begin{align*}a=2\end{align*}$ . $\begin{align*}c=5\end{align*}$ , so we need to find $\begin{align*}b^2\end{align*}$ .
::顶点在 Y 轴上, 因此这是一个垂直的双倍波拉, a=2. c=5, 所以我们需要找到 b2 。

$\begin{aligned} c^{2} & = a^{2} + b^{2} \\ 25 & = 4 + b^{2} \to b^{2} = 21 \end{aligned}$
$\begin{align*}c^2 &= a^2+b^2 \\ 25 &= 4+b^2 \rightarrow b^2=21\end{align*}$
::c2=a2+b225=4+b2=21

The equation of the hyperbola is $\begin{align*}\frac{y^2}{4} - \frac{x^2}{21}=1\end{align*}$ .
::双倍波拉的方程式是y24-x221=1。

Example 3
::例3

asymptote: $\begin{align*}y=x\end{align*}$
::浮点数 y=x

vertex: $\begin{align*}(4, 0)\end{align*}$
::顶点 : (4,0)

Rewriting the slope of $\begin{align*}y=x\end{align*}$ , we get $\begin{align*}y=\frac{1}{1}x\end{align*}$ . So, we know that $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are in a ratio of 1:1. Because the vertex is $\begin{align*}(4, 0)\end{align*}$ , we know that $\begin{align*}a=4\end{align*}$ and that the hyperbola is horizontal. Because $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are in a ratio of 1:1, $\begin{align*}b\end{align*}$ has to equal 4 as well. The equation of the hyperbola is $\begin{align*}\frac{x^2}{16} - \frac{y^2}{16}=1\end{align*}$ .
::重写 y=x 的斜坡, 我们得到 y= 11x 。因此, 我们知道 a 和 b 的比例是 1: 1 。因为顶点是 (4,0 ) 我们知道 a= 4 , 双曲线是水平的。因为 a 和 b 的比例是 1: 1, b 必须等于 4 。超波拉的方程式是 x216 - Y216= 1 。

Example 4
::例4

Find the equations of two hyperbolas, centered at the origin, with different $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ values and an asymptote of $\begin{align*}y=\frac{3}{4}x\end{align*}$ .
::查找两个双螺旋体的方程, 以原点为中心, 具有不同的 a 和 b 值, 以及 Y= 34x 的零星值。

One possibility is that $\begin{align*}b=3\end{align*}$ and $\begin{align*}a=4\end{align*}$ making the equation $\begin{align*}\frac{x^2}{16} - \frac{y^2}{9}=1\end{align*}$ . A second possibility could be that $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are a multiply of the ratio 4:3. So, $\begin{align*}a=8\end{align*}$ and $\begin{align*}b=6\end{align*}$ , making the equation $\begin{align*}\frac{x^2}{64} - \frac{y^2}{36}=1\end{align*}$ .
::一种可能性是 b=3 和 a=4 使方程式x216-y29=1. 第二种可能性是 a 和 b 是 4: 3. 因此, a =8 和 b=6 使方程式x264-y236=1 的乘数。

Review
::回顾

Find the equation of the hyperbola, centered at the origin, given the information below.
::查找双倍波拉的方程式, 以来源为中心, 给出以下信息。

vertex: $\begin{align*}(-2, 0)\end{align*}$ , focus: $\begin{align*}(-5, 0)\end{align*}$
::顶点-2,0),重点-5,0)

vertex: $\begin{align*}(4, 0)\end{align*}$ , focus: $\begin{align*}(7, 0)\end{align*}$
::顶点: (4,0),重点: (7,0)

$\begin{align*}b=8\end{align*}$ , focus: $\begin{align*}(-15, 0)\end{align*}$
::b=8,重点-15,0)

vertex: $\begin{align*}(-6, 0)\end{align*}$ , asymptote: $\begin{align*}y=\frac{4}{3}x\end{align*}$
::顶点 - 6 ) , 空点 : y= 43x

$\begin{align*}b=6\end{align*}$ , focus: $\begin{align*}(0, 11)\end{align*}$
::b=6,重点0,11)

vertex: $\begin{align*}(0, 5)\end{align*}$ , asymptote: $\begin{align*}y=x\end{align*}$
::顶点 : (0, 5) , 空点 : y=x

asymptote: $\begin{align*}y=-\frac{1}{2}x\end{align*}$ , vertex: $\begin{align*}(6, 0)\end{align*}$
::空点 : y12x, 顶点 : (6,0)

asymptote: $\begin{align*}y=3x\end{align*}$ , $\begin{align*}\ b=9\end{align*}$ , vertical transverse axis
::空点 : y= 3x, b= 9, 垂直横轴

vertex: $\begin{align*}(0, 8)\end{align*}$ , focus: $\begin{align*}\left(0, 6 \sqrt{2}\right)\end{align*}$
::顶点: (0,8),重点: (0,62)

Find the equation of two hyperbolas such that they have the same $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ values, the equation of an asymptote is $\begin{align*}y=\frac{4}{5}x\end{align*}$ , and centered at the origin.
::找到两个双倍的方程式, 以便它们具有相同的 a 和 b 值, 小数方程式的方程式是 y= 45x, 以源代码为中心。

Find the equation of two hyperbolas such that they have different $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ values, both horizontal, the equation of an asymptote is $\begin{align*}y=-\frac{2}{3}x\end{align*}$ , and centered at the origin.
::找到两个双倍的方程式, 以便它们具有不同的a值和b值, 两者均为水平值, 单位方程式的方程式是 y23x, 以原点为中心。

Find the equation of two hyperbolas such that they have different $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ values, both vertical, the equation of an asymptote is $\begin{align*}y=6x\end{align*}$ , and centered at the origin.
::查找两个双倍的方程式, 以便它们具有不同的a和b值, 两者都是垂直的, 一个无症状方程式的方程式是y=6x, 以原点为中心。

Find the equation of two hyperbolas such that they have the same $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ values, the equation of an asymptote is $\begin{align*}y=-\frac{10}{7}x\end{align*}$ , and centered at the origin.
::找到两个双倍的方程式, 以便它们具有相同的 a 值和 b 值, 小数方程式的方程式是 y 107x, 以源代码为中心。

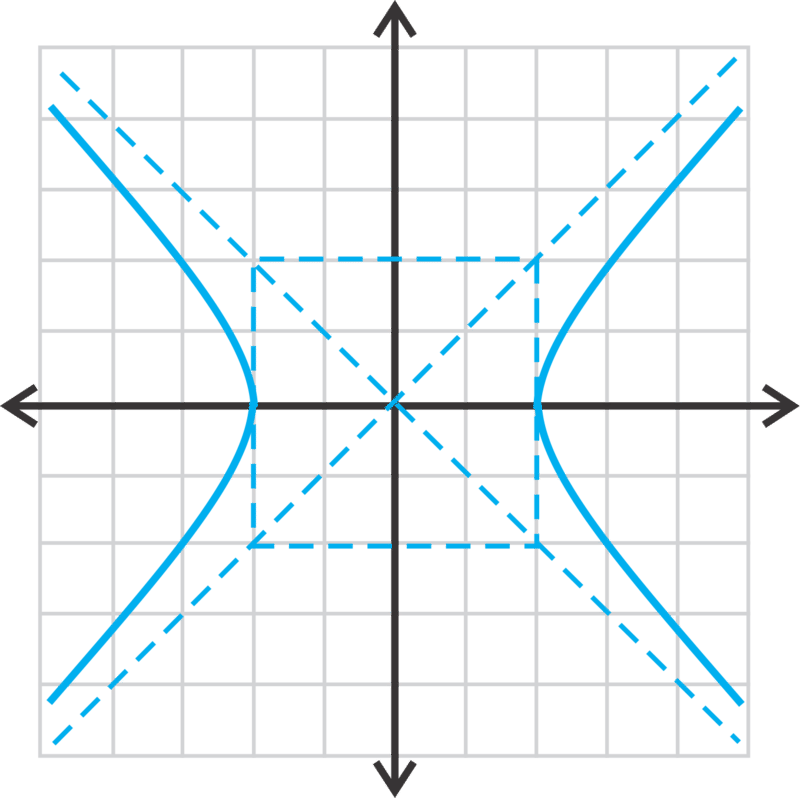
Find the equation of the hyperbolas below.
::找到下方超光子的方程

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

以起源为中心, 写作超波拉的等式

The Equation of a Hyperbola ::超博拉之等式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

The Equation of a Hyperbola
::超博拉之等式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)