课程： 10.10 一般二次赤道

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

普通二次电

You and your friends are playing the game Name the Conic Section. You draw a card with the equation $\begin{align*}x^2 - 4x - 8y + 12 = 0\end{align*}$ . What type of conic section is represented by this equation?
::您和朋友正在玩游戏名称二次曲线部分。您用公式 x2 - 4x- 8y+12=0 绘制一张牌。此公式代表哪种二次曲线部分 ?

Conic Equations
::二次曲线

The equation of any conic section can be written in the form $\begin{align*}Ax^2+Bxy+Cy^2+Dx+Ey+F=0\end{align*}$ , which is the general second-degree equation in terms of $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ . For all the you have seen so far, $\begin{align*}B=0\end{align*}$ because all axes were either horizontal or vertical. When a conic is in this form, you have to complete the square to get it into standard form.
::任何二次曲线部分的方程式可以以 Ax2+Bxy+Cy2+Dx+Ey+F=0 的形式写成,这是以 x 和 y 表示的一般二度方程式。对于迄今所见的所有方程式,B=0,因为所有轴都是水平或垂直的。如果二次曲线是这种形式,则必须填写方形,才能将其变成标准格式。

Standard Form of Conic Sections with Center $\begin{align}(h, k)\end{align}$
::与中(h,k)

	Horizontal Axis	Vertical Axis
Circle	$\begin{align}(x-h)^2+(y-k)^2=r^2\end{align}$
Parabola	$\begin{align}(y-k)^2=4p(x-h)\end{align}$	$\begin{align}(x-h)^2=4p(y-k)\end{align}$
Ellipse	$\begin{align}\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2}=1\end{align}$	$\begin{align}\frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2}=1\end{align}$
	$\begin{align}\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2}=1\end{align}$	$\begin{align}\frac{(y-k)^2}{a^2} + \frac{(x-h)^2}{b^2}=1\end{align}$

Let's determine the type of conic section $\begin{align*}x^2+y^2-6x+10y-6=0\end{align*}$ and rewrite the equation in standard form.
::让我们确定二次曲线区域 x2+y2 - 6x+10y - 6=0 的类型, 并以标准格式重写方程式。

Start by rewriting the equation with the $\begin{align*}x\end{align*}$ terms and $\begin{align*}y\end{align*}$ terms next to each other and moving the constant to the other side of the equation.
::开始重写方程式, 以 x 条件和 y 条件相邻, 并将常数移动到方程式的另一侧。

\begin{aligned} x^{2} + y^{2} - 6 x + 10 y - 6 = 0 \\ (x^{2} - 6 x) + (y^{2} + 10 y) = 6 \end{aligned}

$\begin{align*}x^2+y^2-6x+10y-6=0 \\ (x^2-6x)+(y^2+10y)=6\end{align*}$
::x2+y2 - 6x+10y-6=0(x2 - 6x)+(y2+10y)=6

Now, complete the square for both the $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ terms. To complete the square, you need to add $\begin{align*}\left(\frac{b}{2}\right)^2\end{align*}$ to both sides of the equation.
::现在, 完成 x 和 y 条件的正方形。要完成正方形, 您需要在方程的两侧添加 (b2) 2 。

\begin{aligned} (x^{2} - 6 x + 9) + (y^{2} + 10 y + 25) & = 6 + 9 + 25 \\ (x - 3)^{2} + (y + 5)^{2} & = 40 \end{aligned}

$\begin{align*}(x^2-6x+ {\color{blue}9}) + (y^2+10y+ {\color{red}25})&= 6+ {\color{blue}9}+ {\color{red}25} \\ (x-3)^2+(y+5)^2 &= 40\end{align*}$
:

x2-6x+9)+(y2+10y+25)=6+9+25(x-3)2+(y+5)2=40

By looking at the standard forms above, we can see that this is a circle. Another clue as to what type of conic it is, is that $\begin{align*}A\end{align*}$ and $\begin{align*}C\end{align*}$ are equal in the general second-degree equation.
::通过查看上面的标准表格,我们可以看到这是一个圆圈。另一个关于什么类型的二次曲线的线索是A和C在一般二度方程中是相等的。

Now, let's determine the type of conic section $\begin{align*}20x^2-20y^2-80x+240y+320=0\end{align*}$ and rewrite the equation in standard form.
::现在,让我们来决定二次曲线部分的类型 20x2 - 20y2 - 80x+240y+320=0, 并以标准格式重写方程式。

Using the logic from the previous problem , we can conclude that this conic is not a circle. It is also not a parabola because it has both the $\begin{align*}x^2\end{align*}$ and $\begin{align*}y^2\end{align*}$ terms. Rewrite the equation, grouping the $\begin{align*}x\end{align*}$ terms together, $\begin{align*}y\end{align*}$ terms together, and moving the constant over to the other side. Then, pull out the GCF of each set of terms.
::使用前一个问题的逻辑, 我们可以得出这样的结论: 这个二次曲线不是圆形。它也不是抛物线, 因为它有 x2 和 y2 两个条件。重写方程式, 将 x 术语组合在一起, y 术语组合在一起, 并将常数移到另一边。然后, 将每组条件的 GFSP 拔出。

\begin{aligned} 20 x^{2} - 20 y^{2} - 90 x + 240 y + 320 & = 0 \\ 20 x^{2} - 80 x - 20 y^{2} + 240 y & = - 320 \\ 20 (x^{2} - 4 x) - 20 (y^{2} - 12 y) & = - 320 \end{aligned}

$\begin{align*}20x^2-20y^2-90x+240y+320 &= 0 \\ 20x^2-80x-20y^2+240y &= -320 \\ 20(x^2-4x)-20(y^2-12y)&= -320\end{align*}$
::20x2 - 20y2 - 20y2 - 90x+240y+320=020x2 - 80x - 20y2+240y_ 320(x2 - 4x) - 20(y2 - 12y)______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Now, complete the square for the $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ terms. When determining what constant will “complete the square” for each grouping, don’t forget to multiply the constant by the number outside the parenthesis before adding it to the other side.
::现在, 完成 x 和 y 条件的方块。在确定每个组群的常数将“ 完成方块 ” 时, 不要忘记将常数乘以括号外的数, 然后再添加到另一边。

\begin{aligned} 20 (x^{2} - 4 x) - 20 (y^{2} - 12 y) & = - 320 \\ 20 (x^{2} - 4 x + 4) - 20 (y^{2} - 12 y + 36) & = - 320 + 80 - 720 \\ \frac{20 (x - 2)^{2}}{- 960} - \frac{20 (y - 6)^{2}}{- 960} & = \frac{- 960}{- 960} \\ - \frac{(x - 2)^{2}}{48} + \frac{(y - 6)^{2}}{48} & = 1 \\ \frac{(y - 6)^{2}}{48} - \frac{(x - 2)^{2}}{48} & = 1 \end{aligned}

$\begin{align*}20(x^2-4x)-20(y^2-12y) &=\text{-}320 \\ 20(x^2-4x+ {\color{blue}4})-20(y^2-12y+ {\color{red}36}) &=\text{-}320+ {\color{blue}80}- {\color{red}720} \\ \frac{20(x-2)^2}{\text{-}960} - \frac{20(y-6)^2}{\text{-}960} &= \frac{\text{-}960}{\text{-}960} \\ \text{-}\frac{(x-2)^2}{48} + \frac{(y-6)^2}{48} &=1\\ \frac{(y-6)^2}{48}- \frac{(x-2)^2}{48} &=1\end{align*}$
::20x2-4x)-20(y2-12y)=-32020(x2-4x+4)-20(y2-12y+36)=-320+80-72020(x-2-2)2-960-20(y-6)2-960=-960-960-(x-2)2-248+(y-6)248=1(y-6)248-(x-2)248=(x-2)248=1

We now see that this conic is a hyperbola. Going back the original equation, $\begin{align*}C\end{align*}$ is negative. In order for a general second-degree equation to be a hyperbola, $\begin{align*}A\end{align*}$ or $\begin{align*}C\end{align*}$ (not both) must be negative. If $\begin{align*}A\end{align*}$ and $\begin{align*}C\end{align*}$ are both positive or negative and not equal, the equation represents an ellipse.
::我们现在看到这个二次曲线是一个超大曲线。回到原来的方程, C是负的。要使一般二度方程式变成超大曲线, A 或 C (不是两者兼有)必须是负的。如果 A 和 C 是正或负的, 而不是等同的, 这个方程式代表椭圆。

Finally, let's write the equation of the conic below.
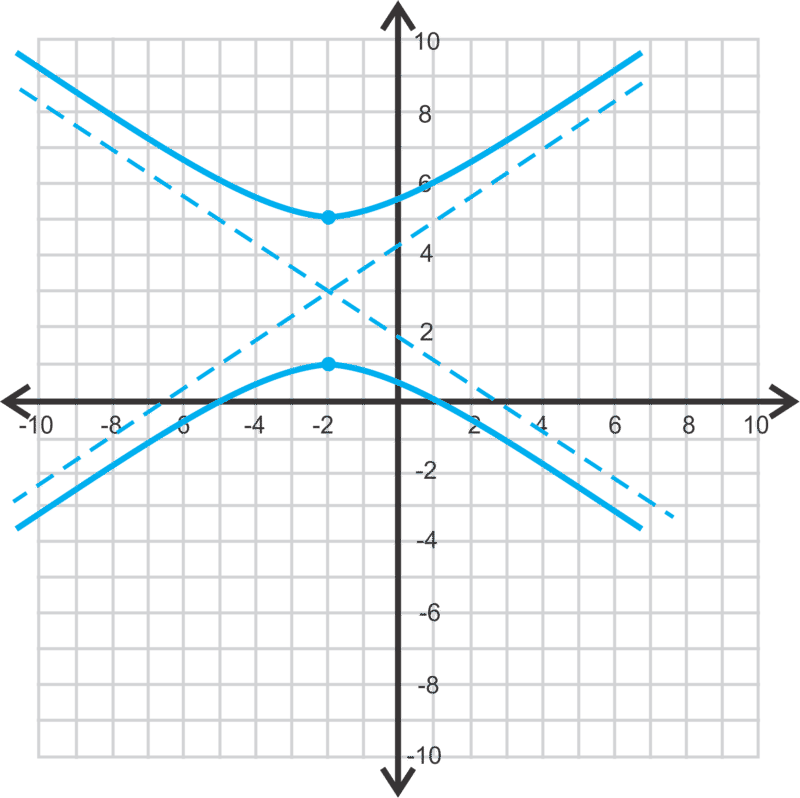
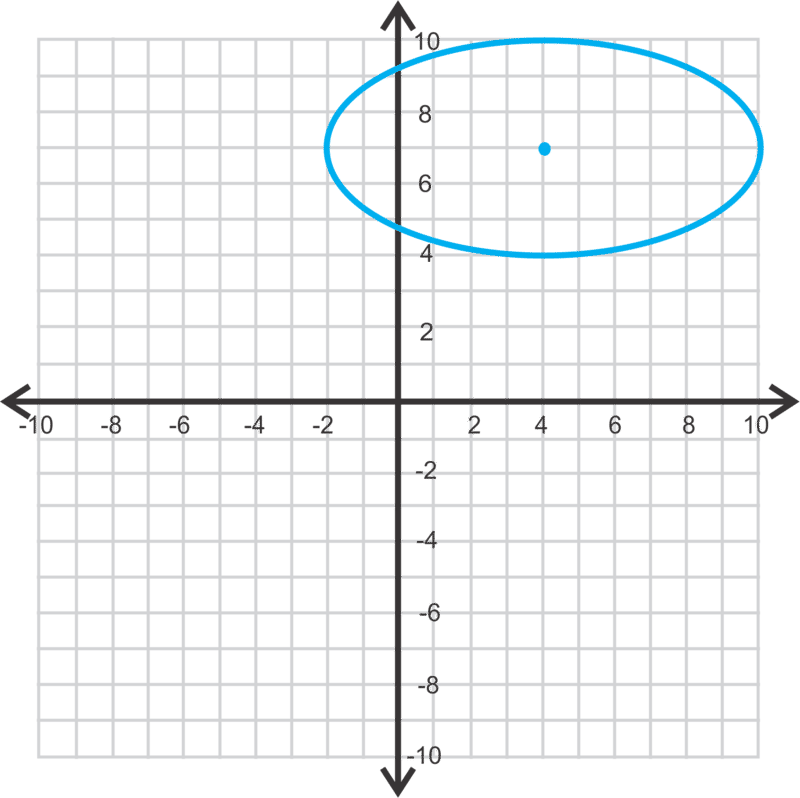
::最后,让我们写下下面的二次曲线的方程式。

Just by looking at the graph, we know this is a horizontal ellipse. The standard equation for this ellipse is $\begin{align*}\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2}=1\end{align*}$ . The center is $\begin{align*}(-3, 6)\end{align*}$ , the major axis is 14 units long, making $\begin{align*}a=7\end{align*}$ , and the minor axis is 6 units long, making $\begin{align*}b=3\end{align*}$ . The equation is therefore $\begin{align*}\frac{(x-(-3))^2}{7^2} + \frac{(y-6)^2}{3^2}=1\end{align*}$ or $\begin{align*}\frac{(x+3)^2}{49} + \frac{(y-6)^2}{4}=1\end{align*}$ .
::通过查看图表,我们知道这是一个水平椭圆。这个椭圆的标准方程式是 (x-h) 2a2+(y-k) 2b2=1. 中心是 (- 3, 6) , 主轴是 14 个单位, 使 a= 7 , 小轴是 6 个单位, 使 b= 3 。因此, 这个方程式是 (x- (-3) 272+(y-6) 232=1 或 (x+3)249+(y-6)24=1 。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine the type of conic section represented by the equation $\begin{align*}x^2 - 4x - 8y + 12 = 0\end{align*}$ .
::早些时候,您被要求确定方程式 x2 - 4x - 8y+12=0 所代表二次曲线段的类型。

Start by rewriting the equation with the $\begin{align*}x\end{align*}$ terms and $\begin{align*}y\end{align*}$ terms next to each other.
::开始重写方程式, 以 x 条件和 Y 条件相邻。

$\begin{align*}x^2-4x = 8y -12\end{align*}$
::x2- 4x=8y- 12

Now, complete the square for the $\begin{align*}x\end{align*}$ terms. To complete the square, we need to add 4 to both sides of the equation.
::现在, 完成 x 条件的方块。要完成方块, 我们需要在方块的两侧增加 4 个。

\begin{aligned} (x^{2} - 4 x + 4) = 8 y - 12 + 4 \\ (x - 2)^{2} = 8 y - 8 \end{aligned}

$\begin{align*}(x^2-4x+ {\color{blue}4}) = 8y -12 + {\color{blue}4}\\ (x-2)^2 = 8y-8\end{align*}$
:

x2-4x+4)=8y-12+4(x-2)2=8y-8

Finally, factor out the LCD from the right side of the equation.
::最后,从方程的右侧计出液晶显示器。

$\begin{align*}(x-2)^2 = 8(y-1)\end{align*}$
:x-2)2=8(y-1)

By looking at the standard forms above, we can see that this is a parabola.
::通过看上面的标准表格,我们可以看到这是一个抛物线。

For Examples 2 & 3, determine the type of conic section and rewrite each equation in standard form.
::对于例2和例3,确定二次曲线段的类型,并以标准格式重写每个方程。

Example 2
::例2

$\begin{align*}9x^2+16y^2+18x-135=0\end{align*}$
::9x2+16y2+18x-135=0

Complete the square. Ellipse.
::完成方形椭圆形

\begin{aligned} 9 x^{2} + 16 y^{2} + 18 x - 135 & = 0 \\ 9 x^{2} + 18 x + 16 y^{2} & = 135 \\ 9 (x^{2} + 2 x + 1) + 16 y^{2} & = 135 + 9 \\ 9 (x + 1)^{2} + 16 y^{2} & = 144 \\ \frac{(x + 1)^{2}}{16} + \frac{y^{2}}{9} & = 1 \end{aligned}

$\begin{align*}9x^2+16y^2+18x-135 &=0 \\ 9x^2+18x+16y^2 &=135 \\ 9(x^2+2x+ {\color{red}1})+16y^2 &=135+ {\color{red}9} \\ 9(x+1)^2+16y^2 &=144 \\ \frac{(x+1)^2}{16} + \frac{y^2}{9} &=1\end{align*}$
::9x2+166y2+18x-135=09x2+18x+166y2=1359(x2+2x+1)+16y2=135+99(x+1)2+16y2=144(x+1)216+y29=1

Example 3
::例3

$\begin{align*}y^2-3x-8y+10=0\end{align*}$
::y2 - 3x-8y+10=0

Complete the square. Parabola.
::完成广场帕拉波拉

\begin{aligned} y^{2} - 3 x - 8 y + 10 & = 0 \\ y^{2} - 8 y - 3 x & = - 10 \\ y^{2} - 8 y + 16 & = 3 x - 10 + 16 \\ (y - 4)^{2} & = 3 x + 6 \\ (y - 4)^{2} & = 3 (x + 2) \end{aligned}

$\begin{align*}y^2-3x-8y+10 &=0 \\ y^2-8y-3x &=-10 \\ y^2-8y+ {\color{red}16} &=3x-10+{\color{red}16} \\ (y-4)^2 &=3x+6 \\ (y-4)^2 &=3(x+2)\end{align*}$
::y2 - 3x - 8y+10=0y2 - 8y - 3x_ 3x_ 10y2 - 8y+16=3x - 10+16(y - 4)2=3x+6(y - 4)2=3(x+2)

Example 4
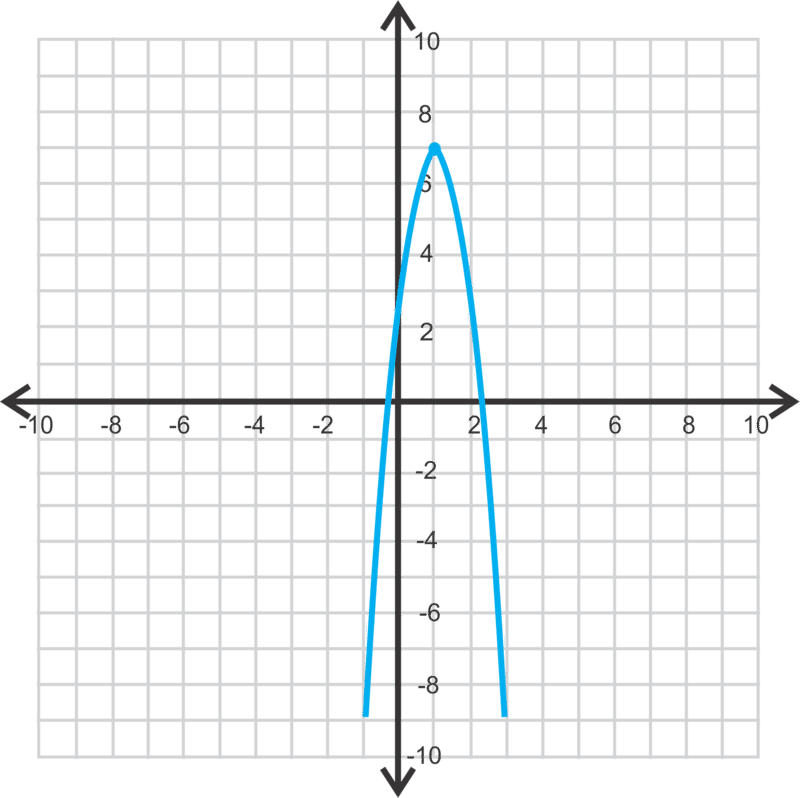
::例4

Write the equation of the conic below.
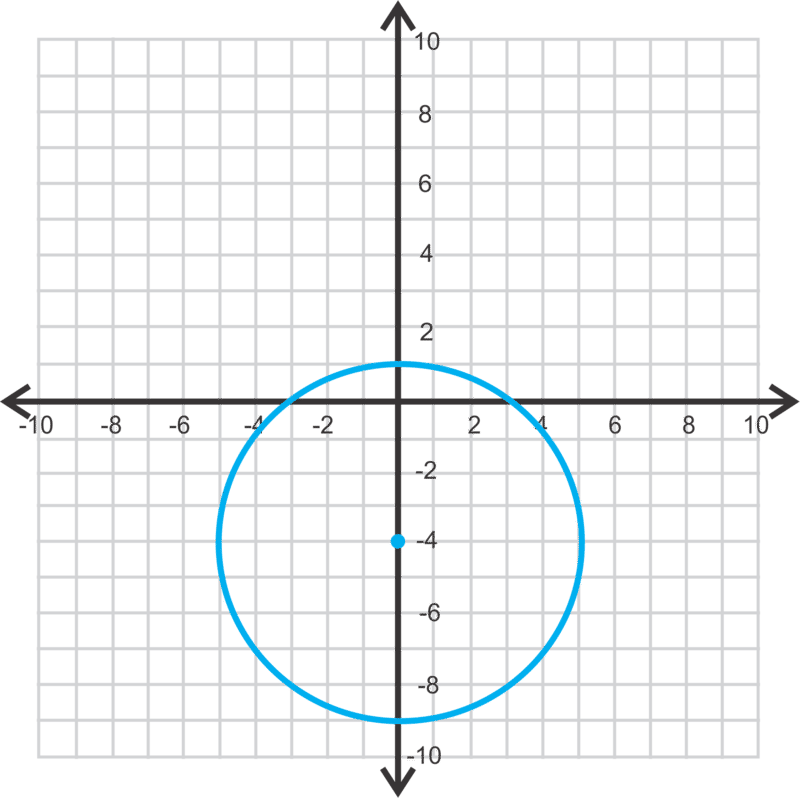
::在下面写下二次曲线的方程。

This is a circle because the distance around the center is the same. The center is $\begin{align*}(0, -4)\end{align*}$ and the radius is 5. The equation is $\begin{align*}x^2+(y+4)^2=25\end{align*}$ .
::这是一个圆, 因为中心周围的距离相同。中心是 0, ~ 4, 半径是 5 。方程式是 x2+(y+4) 2= 25 。

Review
::回顾

In the general conic equation, why does B have to equal zero in order to create a conic?
::在一般二次等式中,为什么B必须等于零才能产生二次等式?

Find the equation of each conic section below.
::查找以下每个二次曲线段的方程。

Rewrite each equation in standard form, classify the conic, and find the center. If the conic is a parabola, find the vertex.
::以标准格式重写每个方程式, 分类二次曲线, 并找到中心。如果二次曲线是抛物线, 请找到顶点。

$\begin{align*}3x^2+3y^2-6x+9y-14=0\end{align*}$
::3x2+3y2-6x+9y-14=0

$\begin{align*}6x^2+12x-y+15=0\end{align*}$
::6x2+12x-y+15=0

$\begin{align*}x^2+2y^2+4x+2y-27=0\end{align*}$
::x2+2y2+4x+2y-27=0

$\begin{align*}x^2-y^2+3x-2y-43=0\end{align*}$
::x2-y2+3x-2y-43=0

$\begin{align*}y^2-8x-6y+49=0\end{align*}$
::y2-8x-6y+49=0

$\begin{align*}-64x^2+225y^2-256x-3150y-3631=0\end{align*}$
::- 64x2+225y2-256x-3150y-3631=0

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

普通二次电

Conic Equations ::二次曲线

Standard Form of Conic Sections with Center ( h , k ) \begin{align*}(h, k)\end{align*} ::与中(h,k)

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)