课程： 10.12 线、四方和二次曲线的溶解系统

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节线条、四面形和二次曲线的溶解系统

折叠展开
线条、四面形和二次曲线的溶解系统
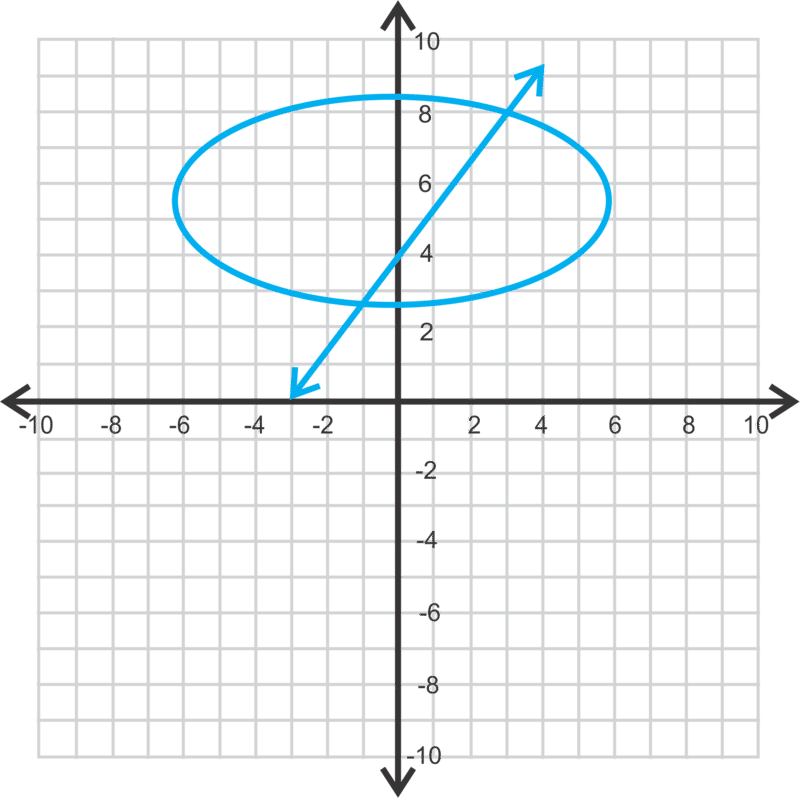
You are given the ellipse $\begin{align*}\frac{x^2}{4} + \frac{y^2}{9} = 1\end{align*}$ and the line $\begin{align*}y = \frac{3}{2}x + 3\end{align*}$ . You want to determine at which point(s), if any, the two equations intersect without graphing. Does the line intersect the ellipse? If so, at which point(s) does it do so?
::您得到了 extlipse x24+y29=1 和 y=32x+3 的线条。您想要确定在哪个点( 如果有的话) , 两个方程式交叉, 而不绘制图形。该线是否交叉了 extlipse ? 如果是的话, 它会在哪个点这样做 ?

Systems of Lines, Quadratics and Conics
::线、四方和二次曲线系统

Previously , we solved a system involving two lines or three planes, by using graphing, substitution, and linear combinations. In this concept, we will add circles, , and to systems of equations. Because both $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ can be squared in these equations, there will often be more than one answer.
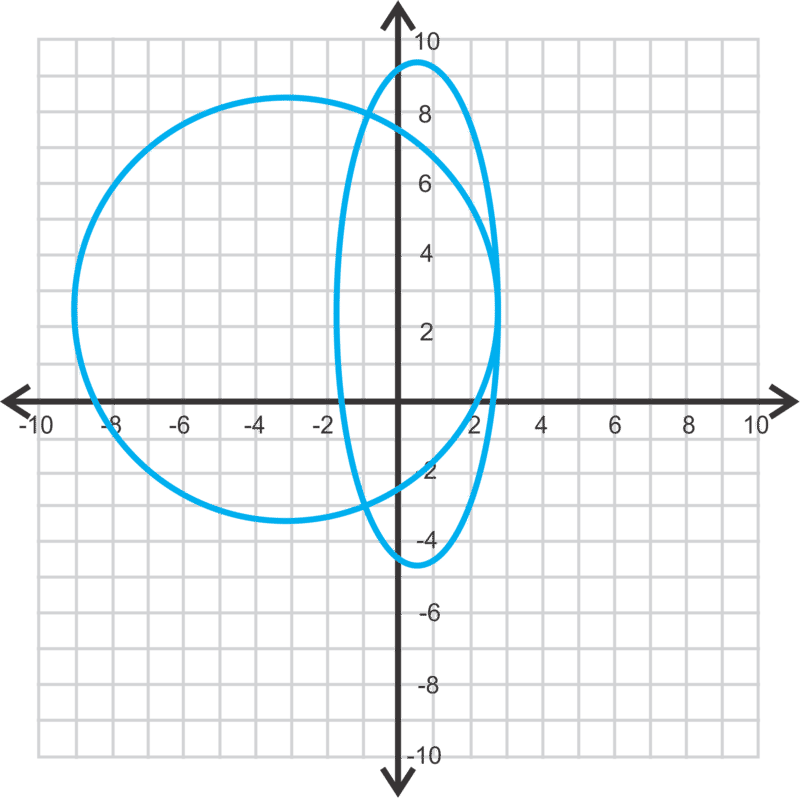
::以前,我们通过图形化、替代和线性组合解决了涉及两行或三平面的系统。在这个概念中,我们将增加圆圈、圆圈和方程系统。由于 x 和 y 都可以在这些方程中方形中方形,因此往往会有一个以上的答案。

Let's estimate the solutions for the system of equations below.
::我们来估计一下下面方程式系统的解决方案

These two ellipses intersect in four places. They look to be the following points:
::这两个省略号在四个地方交叉。它们看起来是以下各点:

$\begin{align*}(0, 7)\end{align*}$ , $\begin{align*}(4.7, 5.5)\end{align*}$ , $\begin{align*}(4.9, 4.3)\end{align*}$ , and $\begin{align*}(-1, 2.9)\end{align*}$
:0,7,47,47,5.5,4.9,4.3)和(-1,2.9)

Keep in mind these are only estimates. In the next problem , we will show how to find the exact answers.
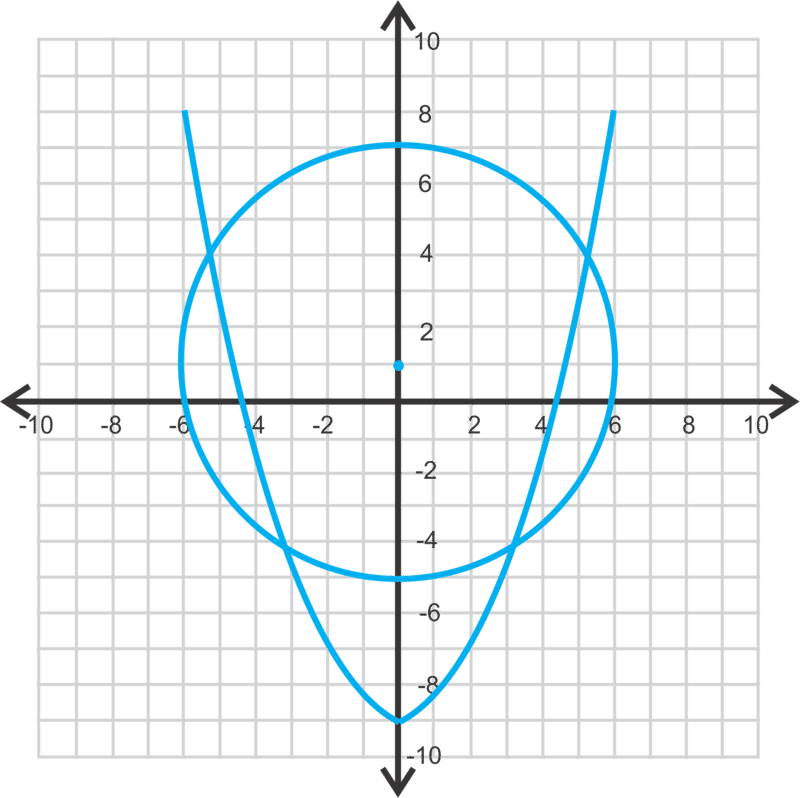
::记住这些只是估计数。在下一个问题上,我们将展示如何找到准确的答案。

Now, let's solve $\begin{align*}x^2+y^2 &=25 \\ 3x+2y &=6\end{align*}$ .
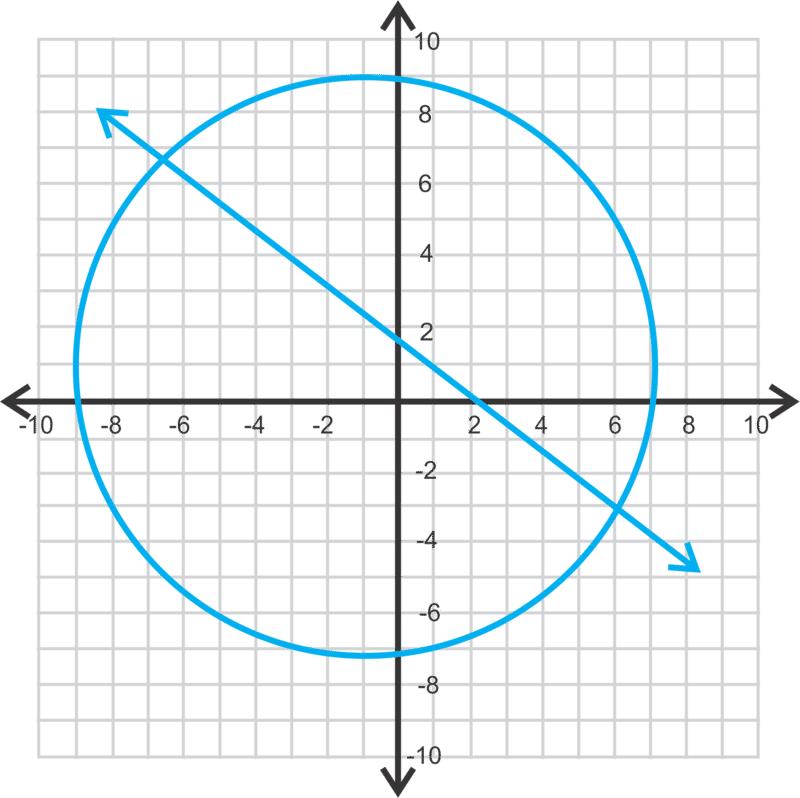
::现在,让我们解决 x2+y2=253x+2y=6。

Let’s solve this system by graphing. The first equation is a circle , centered at the origin, with a radius of 5. The second equation is a line. In slope intercept form, it is $\begin{align*}y=-\frac{3}{2}x+3\end{align*}$ .
::让我们通过图形化来解决这个系统。第一个方程式是一个圆形, 以原点为中心, 半径为 5 。第二个方程式是一条线。在斜坡截击形式中, 是 y32x+3 。

Next, let’s estimate where the line and circle intersect. In the second quadrant, it looks like $\begin{align*}(-1.2, 4.8)\end{align*}$ and in the fourth quadrant it looks like $\begin{align*}(4, -3)\end{align*}$ . These are our estimated answers.
::接下来,让我们来估计线和圆的交叉点。在第二个象体中,它看起来像(-1.2,4.8),在第四个象体中,它看起来像(4,-3),这是我们估计的答案。

To find the exact value of these points of intersection , we need to use substitution. Substitute in the linear equation in for $\begin{align*}y\end{align*}$ into the circle equation and solve for $\begin{align*}x\end{align*}$ .
::要找到这些交叉点的准确值, 我们需要使用替代。在 y 的线性方程中替换 y , 在圆形方程中替换 x 的解析。

$\begin{aligned} x^{2} + {(- \frac{3}{2} x + 3)}^{2} & = 25 \\ x^{2} + \frac{9}{4} x^{2} - 9 x + 9 & = 25 \\ \frac{13}{4} x^{2} - 9 x - 16 & = 0 \\ 13 x^{2} - 36 x - 64 & = 0 \end{aligned}$
$\begin{align*}x^2+\left(-\frac{3}{2}x+3\right)^2 &=25 \\ x^2+\frac{9}{4}x^2-9x+9 &=25 \\ \frac{13}{4}x^2-9x-16 &=0 \\ 13x^2-36x-64 &=0\end{align*}$
::x2+ (- 32x+3) 2= 25x2+94x2- 9x+9= 25134x2- 9x- 16= 013x2- 36x- 64=0

Use the Quadratic Formula:
::使用二次曲线公式 :

$\begin{aligned} x & = \frac{36 \pm \sqrt{36^{2} - 4 (13) (- 64)}}{2 (13)} \\ = \frac{36 \pm \sqrt{4624}}{26} \\ = \frac{36 \pm 68}{26} \end{aligned}$
$\begin{align*}x &= \frac{36 \pm \sqrt{36^2-4(13)(-64)}}{2(13)} \\ &= \frac{36 \pm \sqrt{4624}}{26} \\ &= \frac{36 \pm 68}{26}\end{align*}$
::x=36_362-4(13)(-642(13)=36_462426=36_6826)

The solutions, for $\begin{align*}x\end{align*}$ , are $\begin{align*}\frac{36+68}{26}=4\end{align*}$ and $\begin{align*}\frac{36-68}{26}=-1\frac{3}{13}\end{align*}$ . Plug these into either equation to solve for $\begin{align*}y\end{align*}$ .
::x的解决方案是36+6826=4和36-68261313。

$\begin{align*}y=-\frac{3}{2}(4)+3=-3\end{align*}$ and $\begin{align*}y=-\frac{3}{2} \left(-\frac{16}{13}\right)+3=4 \frac{11}{13}\end{align*}$
::y*32(4)+33和y32(-1613)+3=41113

The points are $\begin{align*}(4, -3)\end{align*}$ and $\begin{align*}\left(-1 \frac{3}{13}, 4 \frac{11}{13}\right)\end{align*}$ .
::要点是(4,-3)和(1313,34,1113)。

The technique used in this problem is how it is recommended you approach each problem. First, graph the system so that you have an idea of how many solutions there are and where they are located. Then, use substitution to solve for the exact answers.
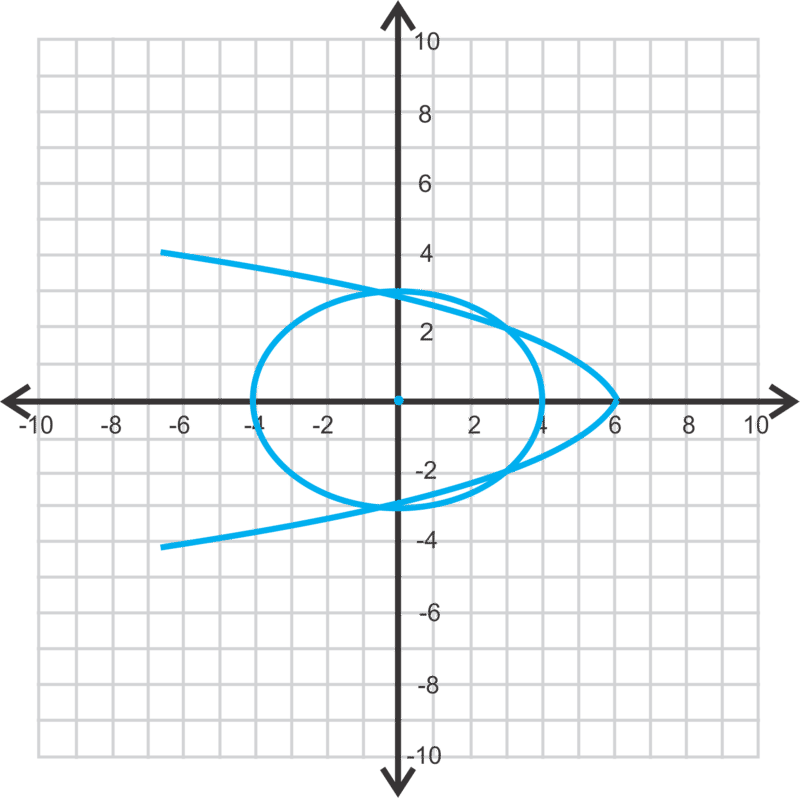
::这个问题所使用的技术是建议您如何处理每个问题。首先, 绘制系统图, 以便您了解有多少解决方案, 以及这些解决方案的位置。然后, 使用替代来解答准确的答案。

Finally, let's solve $\begin{align*}& \frac{x^2}{16} + \frac{y^2}{9}=1 \\ & y^2=-\frac{4}{3}(x-6)\end{align*}$ .
::最后,让我们解析 x216+y29=1y243(x-6)

Graphing the two equations, we have four points of intersection below. The second equation is solved for $\begin{align*}y^2\end{align*}$ , so substitute that into the first equation.
::在绘制两个方程式图时, 我们在下面有四个交叉点。第二个方程式为 y2 解答, 将它替换为第一个方程式。

$\begin{aligned} \frac{x^{2}}{16} - \frac{4 (x - 6)}{3 \cdot 9} & = 1 \\ \frac{x^{2}}{16} - \frac{4 x - 24}{27} & = 1 \\ 27 x^{2} - 16 (4 x - 24) & = 432 \\ 27 x^{2} - 64 x - 48 & = 0 \end{aligned}$
$\begin{align*}\frac{x^2}{16} - \frac{4(x-6)}{3 \cdot 9} &= 1 \\ \frac{x^2}{16} - \frac{4x-24}{27} &=1 \\ 27x^2-16(4x-24) &=432 \\ 27x^2-64x-48 &=0\end{align*}$
::x216-4(x-6)39=1x216-4x-2427=127x2-16(4x-24)=43227x2-64x-48=0

Now, use the Quadratic Formula to solve for $\begin{align*}x\end{align*}$ .
::现在,使用二次曲线公式解析 x。

$\begin{aligned} x & = \frac{64 \pm \sqrt{(- 64)^{2} - 4 (27) (- 48)}}{2 (27)} \\ = \frac{64 \pm \sqrt{9280}}{54} \\ = \frac{32 \pm 4 \sqrt{145}}{27} \end{aligned}$
$\begin{align*}x &= \frac{64 \pm \sqrt{(-64)^2-4(27)(-48)}}{2(27)} \\ &= \frac{64 \pm \sqrt{9280}}{54} \\ &= \frac{32 \pm 4 \sqrt{145}}{27}\end{align*}$
::x=64(-64)2-4(27)(-482(27)=64-928054=32-414527)

Plugging these into the calculator we get $\begin{align*}x = \frac{32+4 \sqrt{145}}{27} \approx 2.97\end{align*}$ and $\begin{align*}x = \frac{32-4 \sqrt{145}}{27} \approx -0.6\end{align*}$ . Looking at the graph, we know that there will be two different $\begin{align*}y\end{align*}$ -values for each $\begin{align*}x\end{align*}$ -value to give four points of intersection. Using the estimations, solve for $\begin{align*}y\end{align*}$ . You can choose either equation.
::将这些插进计算器中, 我们得到 x=32+414527\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x=32\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\计算计算器我们得到的 x=32 -\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

$\begin{aligned} y^{2} & = - \frac{4}{3} (2.97 - 6) y^{2} = - \frac{4}{3} (- 0.6 - 6) \\ y^{2} & = 4.04 a n d y^{2} = 8.8 \\ y & = \pm 2.01 y = \pm 2.97 \end{aligned}$
$\begin{align*}y^2 &= -\frac{4}{3}(2.97-6) \qquad \qquad \quad \quad y^2= -\frac{4}{3}(-0.6-6) \\ y^2 &= 4.04 \qquad \qquad \qquad and \qquad \ y^2= 8.8 \\ y &= \pm 2.01 \qquad \qquad \qquad \qquad \quad \ \ y= \pm 2.97\end{align*}$
::y2 y2 (- 0. 6-6)y2= 4. 4 y2 y2= 8. 8 y@ 2. 01 y2. 97

The points are $\begin{align*}(2.97, 2.01)\end{align*}$ , $\begin{align*}(2.97, -2.01)\end{align*}$ , $\begin{align*}(-0.6, 2.97)\end{align*}$ , and $\begin{align*}(-0.6, -2.97)\end{align*}$ .
::这些点是(2.972.01)、2.97-2.01、(-0.6,2.97)和(-0.6,-2.97)。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine if the line $\begin{align*}y = \frac{3}{2}x + 3\end{align*}$ intersects the ellipse $\begin{align*}\frac{x^2}{4} + \frac{y^2}{9} = 1\end{align*}$ , and if so, at which point(s).
::早些时候,您被要求确定 y= 32x+3 线是否将椭圆 x24+y29=1 相交, 如果是的话, 在哪个点上。

First, let's get rid of the fractions in the equation of the ellipse to make it easier to work with. To do so, we multiply by the LCD.
::首先,让我们除去椭圆方程式中的分数, 以便更容易工作。为了做到这一点, 我们乘以液晶。

$\begin{aligned} \frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 \\ 36 \frac{x^{2}}{4} + 36 \frac{y^{2}}{9} = 36 \cdot 1 \\ 9 x^{2} + 4 y^{2} = 36 \end{aligned}$
$\begin{align*} \frac{x^2}{4} + \frac{y^2}{9} = 1\\ 36 \frac{x^2}{4} + 36 \frac{y^2}{9} = 36 \cdot 1\\ 9x^2 + 4y^2 = 36\end{align*}$
::x24+y29=136x24+36y29=36_19x2+4y2=36

Now we can substitute the equation of the line $\begin{align*}y = \frac{3}{2}x + 3\end{align*}$ in for y and solve for x .
::现在,我们可以用 Y 替换 y = 32x+3 线的方程式, 并用 x 解析。

$\begin{aligned} 9 x^{2} + 4 (\frac{3}{2} x + 3)^{2} = 36 \\ 9 x^{2} + 4 (\frac{9}{4} x^{2} + 9 x + 9) = 36 \\ 9 x^{2} + 9 x^{2} + 36 x + 36 = 36 \\ 18 x^{2} + 36 x = 0 \\ 18 x (x + 2) = 0 \end{aligned}$
$\begin{align*}9x^2 + 4(\frac{3}{2}x + 3)^2 = 36\\ 9x^2 + 4(\frac{9}{4}x^2 + 9x + 9) = 36\\ 9x^2 + 9x^2 + 36x + 36 = 36\\ 18x^2 + 36x = 0\\ 18x(x + 2) = 0\\\end{align*}$
::9x2+4( 32x+3) 2=369x2+4( 94x2+9x+9)=369x2+9x2+9x2+36x+36=3618x2+36x=018x( x+2)=0

So, $\begin{align*}x = 0\end{align*}$ or $\begin{align*}x = -2\end{align*}$
::x=0 或 x2

Finally we can substitute these x values into the equation of the line to find the corresponding y values.
::最后,我们可以将这些 x 值替换为线的方程, 以找到相应的 y 值。

$\begin{align*}y = \frac{3}{2}(0) + 3 = 3 \end{align*}$
::y=32(0)+3=3

$\begin{align*}y = \frac{3}{2}(-2) + 3 = 0\end{align*}$
::y32(-2)+3=0

Therefore, the line intersects the ellipse at points $\begin{align*}(0, 3)\end{align*}$ and $\begin{align*}(-2, 0)\end{align*}$ .
::因此,该线在点(0.3)和点(-2,0)交叉了椭圆。

Example 2
::例2

Estimate the solutions to the system below.
::下文对系统的解决办法作出估计。

$\begin{align*}(3, -0.1)\end{align*}$ and $\begin{align*}(4.5, -6)\end{align*}$
:3,-0.1)和(4.5,-6)

Find the solutions to the systems below.
::找到以下系统的解决办法。

Example 3
::例3

$\begin{aligned} x^{2} + (y - 1)^{2} & = 36 \\ x^{2} & = 2 (y + 9) \end{aligned}$
$\begin{align*}x^2+(y-1)^2 &= 36 \\ x^2 &= 2(y+9)\end{align*}$
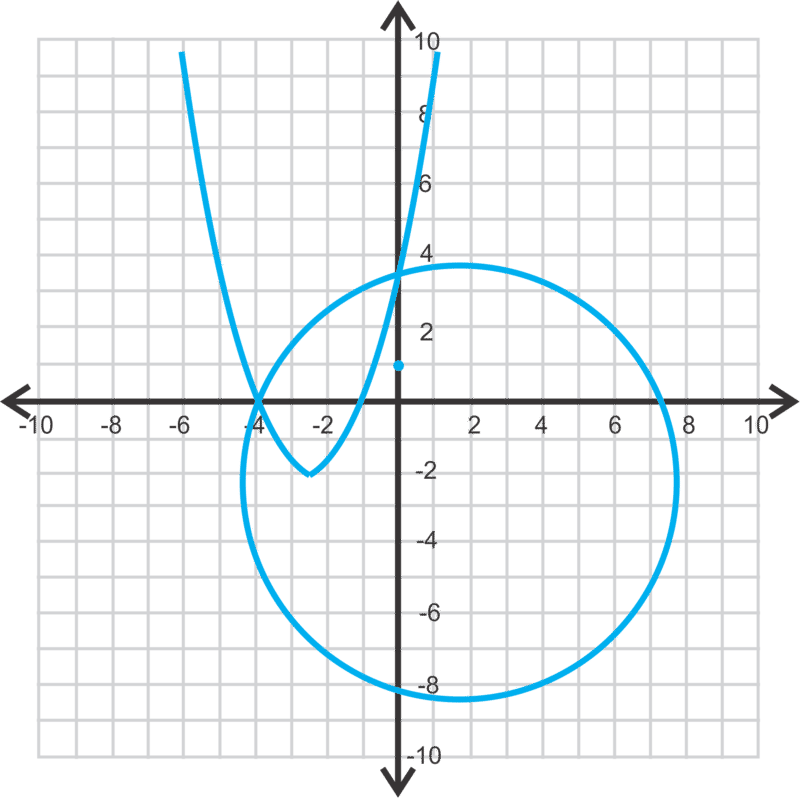
::x2+(y- 1)2=36x2=2(y+9)

This is a circle and a parabola that intersects in four places.
::这是一个圆形和一个抛物线,在四个地方交叉。

Using substitution for $\begin{align*}x^2\end{align*}$ , we have:
::使用 x2 的替代, 我们有:

$\begin{aligned} 2 (y + 9) + (y - 1)^{2} & = 36 \\ 2 y + 18 + y^{2} - 2 y + 1 & = 36 \\ y^{2} & = 17 \\ y & = \pm \sqrt{17} \approx \pm 4.12 \end{aligned}$
$\begin{align*}2(y+9)+(y-1)^2 &=36 \\ 2y+18+y^2-2y+1 &=36 \\ y^2 &= 17 \\ y &= \pm \sqrt{17} \approx \pm 4.12\end{align*}$
::2(y+9)+(y-1)2=362y+18+y2-2y+1=36y2=17y=17_174.12

The corresponding $\begin{align*}x\end{align*}$ -values are:
::相应的x值为:

$\begin{aligned} x^{2} & = 2 (4.12 + 9) x^{2} = 2 (- 4.12 + 9) \\ x^{2} & = 26.25 a n d x^{2} = 9.76 \\ x & = \pm 5.12 x = \pm 3.12 \end{aligned}$
$\begin{align*}x^2 &= 2(4.12+9) \qquad \qquad \quad x^2= 2(-4.12+9) \\ x^2 &= 26.25 \qquad \qquad and \qquad x^2= 9.76 \\ x &= \pm 5.12 \qquad \qquad \qquad \quad \ \ x= \pm 3.12\end{align*}$
::x2=2( 4.12+9)x2=2(- 4.12+9)x2=26.25和x2=9.76x=5.12x3.12

The solutions are: $\begin{align*}(4.12, 5.12)\end{align*}$ , $\begin{align*}(4.12, -5.12)\end{align*}$ , $\begin{align*}(-4.12, 3.12)\end{align*}$ and $\begin{align*}(-4.12, -3.12)\end{align*}$ .
::解决办法是4.12,5.12),(4.12,-5.12),(4.12,3.12)和(4.12,-3.12)。

Example 4
::例4

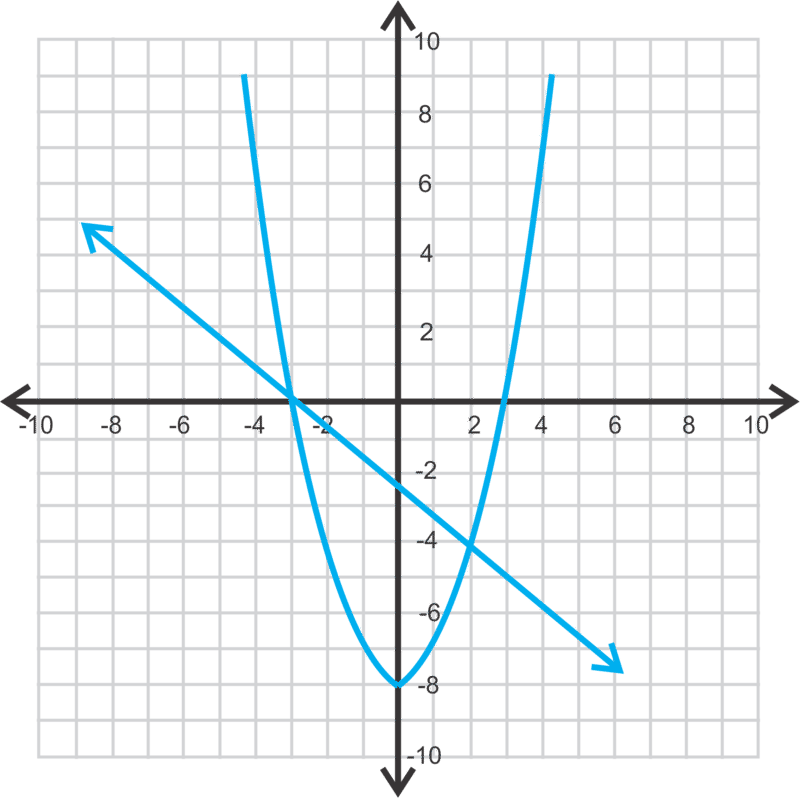
$\begin{aligned} x^{2} & = y + 8 \\ 4 x + 5 y & = 12 \end{aligned}$
$\begin{align*}x^2 &=y+8 \\ 4x+5y &= 12\end{align*}$
::x2=y+84x+5y=12

This is a line and a parabola that intersect in two points.
::这是一条线和一条抛物线,两点相交。

Solve the first equation for $\begin{align*}y\end{align*}$ and substitute into the second.
::解决y的第一个方程式替换为第二个方程式

$\begin{aligned} 4 x + 5 (x^{2} - 8) & = 12 \\ 4 x + 5 x^{2} - 40 & = 12 \\ 5 x^{2} + 4 x - 52 & = 0 \\ x & = \frac{- 4 \pm \sqrt{4^{2} - 4 (5) (- 52)}}{2 (5)} \\ x & = \frac{- 4 \pm \sqrt{1056}}{10} \approx 3.65, 2.85 \end{aligned}$
$\begin{align*}4x+5(x^2-8) &=12 \\ 4x+5x^2-40 &=12 \\ 5x^2+4x-52 &=0 \\ x &= \frac{-4 \pm \sqrt{4^2-4(5)(-52)}}{2(5)} \\ x &= \frac{-4 \pm \sqrt{1056}}{10} \approx 3.65,2.85\end{align*}$
::4x+5(x2-8) = 124x+5x2-40= 125x2+4x-52=0x}442-4(5)(-52) (5)x41056103.65.2.85

Using the first equation, $\begin{align*}y=3.65^2-8=5.32\end{align*}$ and $\begin{align*}y = 2.85^2-8=0.12\end{align*}$ . The points are $\begin{align*}(3.65, 5.32)\end{align*}$ and $\begin{align*}(2.85, 0.12)\end{align*}$ .
::使用第一个方程,y=3.652-8=5.32和y=2.852-8=0.12。点分别为(3.65,5.32)和(2.85,0.12)。

Review
::回顾

Estimate the solutions for each system of equations below.
::估计以下每一方程式系统的解决办法。

Solve each system of equations below.
::解决下方方程式的每一个系统。

.

$\begin{aligned} 5 x^{2} + 3 y & = 17 \\ x - y & = 1 \end{aligned}$
$\begin{align*}5x^2+3y &= 17 \\ x-y &= 1\end{align*}$

.

$\begin{aligned} x^{2} + y^{2} & = 7.5 \\ x + 2 y & = 6 \end{aligned}$
$\begin{align*}x^2+y^2 &= 7.5 \\ x+2y &= 6\end{align*}$

.

$\begin{aligned} x^{2} & = y + 4 \\ \frac{x^{2}}{4} + (y + 2)^{2} & = 1 \end{aligned}$
$\begin{align*}x^2 &= y+4 \\ \frac{x^2}{4}+(y+2)^2 &= 1\end{align*}$

.

$\begin{aligned} (x - 1)^{2} + (y - 3)^{2} & = 25 \\ x^{2} & = - 2 (y - 10) \end{aligned}$
$\begin{align*}(x-1)^2+(y-3)^2 &= 25 \\ x^2 &= -2(y-10)\end{align*}$

.

$\begin{aligned} x^{2} + y^{2} & = 16 \\ 4 x - 3 y & = 18 \end{aligned}$
$\begin{align*}x^2+y^2 &=16 \\ 4x-3y &= 18\end{align*}$

.

$\begin{aligned} (x + 4)^{2} + (y + 1)^{2} & = 36 \\ \frac{(x + 1)^{2}}{4} + \frac{(y - 2)^{2}}{25} & = 1 \end{aligned}$
$\begin{align*}(x+4)^2+(y+1)^2 &= 36 \\ \frac{(x+1)^2}{4} + \frac{(y-2)^2}{25} &= 1\end{align*}$

How many different ways can a circle and a parabola intersect? Draw each possibility.
::圆形和抛物线交错有多少种不同的方式? 绘制每一种可能性。

How many different ways can a circle and an ellipse intersect? Draw each possibility.
::圆形和椭圆交叉可以有多少种不同的方式? 绘制每一种可能性。

Create a system of two circles with no solution. What would the graph look like?
::创建一个由两个圆组成的系统, 没有解决方案。图形会是什么样子 ?

Challenge Find the solutions for the system
::为系统找到解决办法的挑战

$\begin{aligned} x^{2} + y^{2} & = r^{2} \\ y & = m x \end{aligned}$
$\begin{align*}x^2+y^2 &= r^2 \\ y &= mx\end{align*}$
::x2+y2=r2y=mx

Leave your answers in terms of $\begin{align*}m\end{align*}$ and $\begin{align*}r\end{align*}$ .
::留下你的答案以m和r。

Challenge Determine if the system of three equations below have one common solution.
::确定以下三个方程式系统是否有一个共同的解决办法。

$\begin{aligned} x^{2} + 3 y^{2} & = 16 \\ 3 x^{2} + y^{2} & = 16 \\ y & = x \end{aligned}$
$\begin{align*}x^2+3y^2 &= 16 \\ 3x^2+y^2 &= 16 \\ y &= x\end{align*}$
::x2+3y2=163x2+y2=16y=x

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

线条、四面形和二次曲线的溶解系统

Systems of Lines, Quadratics and Conics ::线、四方和二次曲线系统

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Systems of Lines, Quadratics and Conics
::线、四方和二次曲线系统

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)