章节大纲

  • 常规

    全部折叠 展开全部

  • 简单和复合利息

    Suppose you are re-negotiating an allowance with your parents. Currently you are given $25 per week, but it is the first of June, and you have started mowing the lawn and taking out the trash every week. You think your allowance should be increased.
    ::假设你正在与父母重新谈判津贴。现在,你每周得到25美元,但这是6月1日,你开始修剪草坪,每星期清除垃圾。你认为你的津贴应该增加。

    Your father considers the situation and makes you the following offer:
    ::你父亲会考虑情况 并给你以下条件:

    "I tell you what. I will give you three options for your allowance, you tell me which you would like"
    ::"我告诉你,我会给你三个选择 来支付你的津贴,你告诉我你想要什么"

    "Option A: You keep earning  $25 per week."
    ::"备选A:你每周挣25美元"

    "Option B: You take $15 this week, then $16 next week, and so on. I'll continue adding $1 per week until the  last week of the year (which is 30 weeks) ."
    ::选项B:你这周拿15美元,下周16美元,等等。我将继续每周加1美元,直到今年的最后一周(即30周)为止。”

    "Option C: I'll give you 1 penny this week, and then double your allowance each week until the first of October which is 17 weeks away. You'll be paid whatever that rate is for the rest of the year."
    ::选择C:我这周给你一分钱, 然后每星期加倍你的津贴,直到10月1日, 也就是17周之后的10月1日,

    Which option would you choose?
    ::你会选择哪一种选择?

    Simple and Compound Interest
    ::简单和复合利息

    is interest which accrues based only on the principal of an investment or loan . The simple interest is calculated as a percent of the principal.
    ::即只根据投资或贷款本金计算的利息,简单利息按本金的%计算。

    Simple Interest: i = p ⋅ r ⋅ t .
    ::简单利息:i=prt。

    Variable i is interest, p represents the principal amount, r represents the interest rate, and t represents the amount of time the interest has been accruing. For example, say you borrow $2,000 from a family member, and you insist on repaying with interest. You agree to pay 5% interest, and to pay the money back in 3 years.
    ::变量 i 是利息, p 代表本金金额, r 代表利率, t 代表利息累积的时间。 例如, 说您从家庭成员那里借了 2 000 美元, 您坚持用利息偿还。 您同意支付5% 的利息, 并在三年后还清 。

    The interest you will owe will be 2000(0.05)(3) = $300. This means that when you repay your loan, you will pay $2300. Note that the interest you pay after 3 years is not 5% of the original loan, but 15%, as you paid 5% of $2000 each year for 3 years.
    ::您将拖欠的利息为 2000( 0.05 ) (3) = 300 美元。 这意味着当您偿还贷款时, 您将支付2300 美元。 请注意, 3 年后您支付的利息不是原始贷款的5%, 而是15%, 因为在3 年中您每年支付2 000美元中的5% 。

    Now let’s consider an example in which interest is compounded. Say that you invest $2000 in a bank account, and it earns 5% interest annually. How much is in the account after 3 years?
    ::现在让我们来举一个利息复加的例子。 假设你在银行账户上投资了2 000美元,每年赚取5 % 的利息。 3年后,该账户的利息是多少?

    Compound interest: A ( t ) = p ⋅ ( 1 + r ) t
    ::复利: A( t) =p( 1+r) t

    Here, A ( t ) is the A mount in the account after a given t ime in years, p rincipal is the initial investment, and r ate is the interest rate. Note that we use ( 1 + r ) instead of just r , so we can find the entire amount in the account, not just the interest paid.
    ::在这里, A( t) 是特定年份时间后账户中的金额, 本金是初始投资, 利率是利率 。 注意我们使用(1+r) 而不是只使用 r, 这样我们就可以在账户中找到全部金额, 而不仅仅是支付的利息 。

    A ( t ) = 2000 ⋅ ( 1.05 ) 3
    ::A(t) = 2000(1.053)3

    After three years, you will have $2315.25 in the account, which means that you will have earned $315.25 in interest.
    ::三年后,你将有2315.25美元入帐,这意味着你将赚取315.25美元的利息。

    Compounding results in more interest because the principal on which the interest is calculated increased each year. Another way to look at it is that compounding creates more interest because you are earning interest on interest, and not just on the principal.
    ::复利导致更多的兴趣,因为计算利息的本金每年会增加。 另一种观点是,复利会产生更多的兴趣,因为你正在赚取利息利息,而不仅仅是本金利息。

    Examples
    ::实例

    Example 1
    ::例1

    Earlier, you were asked which allowance option you would choose.
    ::早些时候,有人问你会选择哪种津贴选择。

    Assume you want to make the most money possible and  that there are 30 weeks left until the end of the year.
    ::假设你想尽量赚钱 并且还有30周时间到年底

    Option A = 25 ⋅ 30 = $ 750 total
    ::备选A=2530=750美元共计

    Option B = 15 + 16 + 17... + 45 = $ 930 total
    ::备选B=15+16+17...+45=930美元

    Option C (assuming 17 weeks until Oct. 1 st ) = $ 0.01 ⋅ ( 2 17 ) = $ 1 , 310.72 each week after Oct 1 st
    ::备选办法C(假设17周至10月1日)=0.01 (217美元)=10月1日之后的一周1 310.72美元

    It is entirely possible that dear old dad didn't take seriously enough, he may need a second job!
    ::这完全有可能,亲爱的老爹没有 足够认真对待, 他可能需要第二份工作!

    Example 2
    ::例2

    Use the formula for compound interest to determine the amount of money in an investment after 20 years, if you invest $2000, and the interest rate is 5% compounded annually.
    ::使用复合利息公式来确定20年后投资金额,如果投资2 000美元,利率每年增加5%。

    The investment will be worth $5306.60.
    ::投资价值5306.60美元

    A(t) = P(1 + r) t
    ::A(t)=P(1+r)t

    A(20) = 2000(1.05) 20
    ::A(20) = 2000(1.05)20

    A(20) = $5306.60
    ::A(20) = 5306.60

    Example 3
    ::例3

    How long will it take for $2000, invested at 5% compounded annually, to reach $7,000?
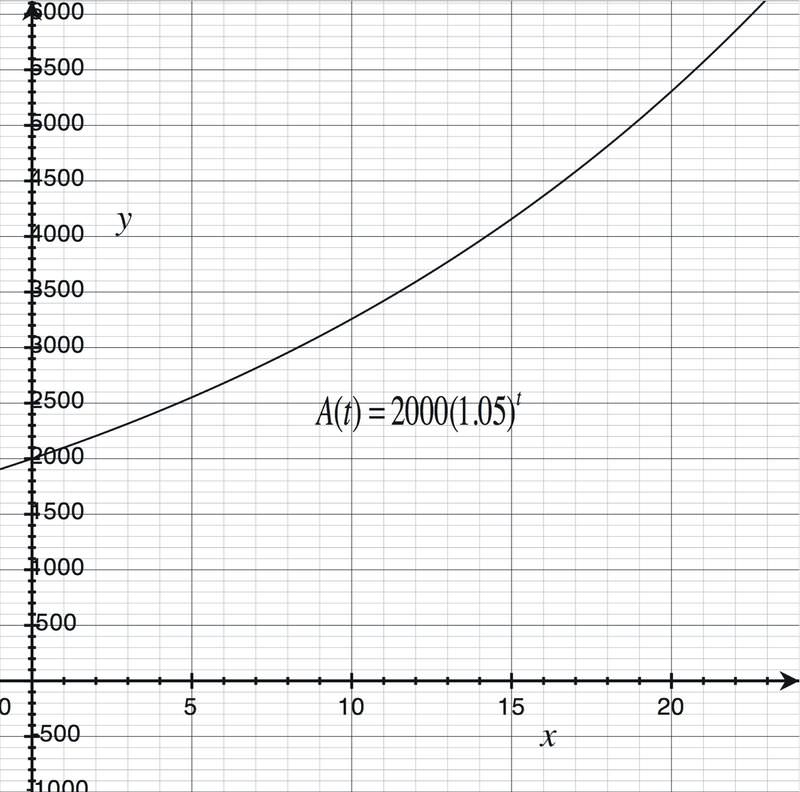
    ::两千元投资需要多久才能达到七千美元?

    If we graph the function A(t) = 2000(1.05) t , we can see the values for any number of years.
    ::如果我们图形显示函数A(t) = 2000(1.05t),我们可以看到任何年份的值。

    If you graph this function using a graphing calculator, you can determine the value of the investment by tracing along the function, or by pressing on your graphing calculator and then entering an x value.
    ::如果您使用图形计算器来图形显示此函数,您可以通过沿着函数跟踪,或者按下图形计算器然后输入 x 值来确定投资的价值。

    You can also choose an investment value you would like to reach, and then determine the number of years it would take to reach that amount. Find the intersection of the exponential function with the line y = 7000.
    ::您也可以选择您想要达到的投资值,然后确定达到该数值需要多少年。找到指数函数与Y = 7000线的交叉点。

    lesson content

    You can see here that the line and the curve intersect at a little less than x = 26. Therefore it would take almost 26 years for the investment to reach $7000.
    ::您可以在这里看到线和曲线在小于x=26时交错, 因此投资需要近26年才能达到7000美元。

    Example 4
    ::例4

    What is the value of an investment after 20 years, if you invest $2000, and the interest rate is 5% compounded continuously ?
    ::投资20年后的价值是多少? 如果你投资2000美元, 利率是5%,

    The more often interest is compounded, the more it increases, but there is a limit. Each time you increase the number of compoundings, you decrease the fraction of the annual interest that is applied to each compounding. Eventually, the differences become so small as to be negligible. This is known as continuous compounding .
    ::利息越是复杂,利息增加越多,但有限度。每次增加化合物数量,就会减少每种化合物年利息的一小部分。最终,差异变得很小,以至于微不足道。这被称为连续化合物。

    The function A ( t ) = Pe rt is the formula we use to calculate the amount of money when interest is continuously compounded, rather than interest that is compounded at discrete intervals, such as monthly or quarterly.
    ::函数 A(t) = Pert 是指当利息持续增加时我们用来计算金额的公式,而不是在每月或季度等离散间隔(如月度或季度)中复合的利息。

    A ( t ) = Pe rt
    ::A(t) = 珀尔特

    A (20) = 2000 e .05(20)
    ::A(20) = 2000e.05(20)

    A (20) = 2000 e 1
    ::A(20) = 2000e1

    A (20) = $5436.56
    ::A(20)=5436.56美元

    Example 5
    ::例5

    Compare the values of the investments shown in the table. If everything else is held constant , how does the compounding influence the value of the investment?
    ::比较表格中显示的投资价值。 如果其他一切保持不变, 复合会如何影响投资的价值 ?

      Principal r n t
    a. $4,000 .05 1 (annual) 8
    b. $4,000 .05 4 (quarterly) 8
    c. $4,000 .05 12 (monthly) 8
    d. $4,000 .05 365 (daily) 8
    e. $4,000 .05 8760 (hourly) 8

    Use the compound interest formula. For this example, the n is the quantity that changes: A ( 8 ) = 4000 ( 1 + .05 n ) 8 n
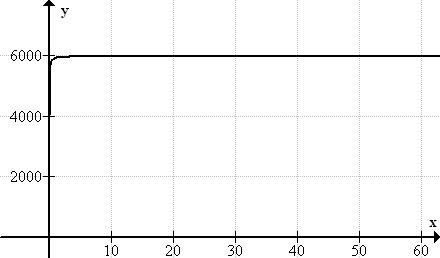
    ::使用复方利息公式。 对于此示例, n 是更改的数量 : A( 8) = 40000(1+. 05n) 8n

      Principal r n t A
    a. $4,000 .05 1 (annual) 8 $5909.82
    b. $4,000 .05 4 (quarterly) 8 $5952.52
    c. $4,000 .05 12 (monthly) 8 $5962.34
    d. $4,000 .05 365 (daily) 8 $5967.14
    e. $4,000 .05 8760 (hourly) 8 $5967.29

    A graph of the function f ( x ) = 4000 ( 1 + .05 x ) 8 x is shown below:
    ::函数f( x) = 40000(1+. 05x) 8xis 图表如下:

    The graph seems to indicate that the function has a horizontal asymptote at $6000. However, if we zoom in, we can see that the horizontal asymptote is closer to 5967.
    ::图表似乎显示该函数的水平零点为6000美元。然而,如果我们放大,我们可以看到,水平零点接近5967美元。

    lesson content

    What does this mean? This means that for the investment of $4000, at 5% interest, for 8 years, compounding more and more frequently will never result in more than about $5968.00.
    ::这意味着,对于4000美元的投资,即5%的利息,8年的投资,增加的频率越来越频繁,不会超过5968.00美元。

    Example 6
    ::例6

    Determine the value of each investment.
    ::确定每项投资的价值。

    1. You invest $5000 in an account that gives 6% interest, compounded monthly. How much money do you have after 10 years?
      ::你投资了5000美元在一个账户中,该账户提供6%的利息,每月复计。十年后你有多少钱?

    $5000, invested for 10 years at 6% interest, compounded monthly.
    ::投资10年, 利息6%, 每月复数。

    A ( t ) = P ( 1 + r n ) n t
    ::A(t) = P(1+rn)

    A ( 10 ) = 5000 ( 1 + .06 12 ) 12 ⋅ 10
    ::A(10)=5000(1+.0612+.0612)12_10

    A ( 10 ) = 5000 ( 1.005 ) 120
    ::A(10)=500000(1.005)120

    A ( 10 ) = $ 9096.98
    ::A(10)=9096.98美元

    1. You invest $10,000 in an account that gives 2.5% interest, compounded quarterly. How much money do you have after 10 years?
      ::你投资一万元到一个账户里 提供2.5%的利息, 每季度复计。十年后你有多少钱?

    $10000, invested for 10 years at 2.5% interest, compounded quarterly.
    ::1 000美元,投资10年,利息2.5%,每季度一次。

    Quarterly compounding means that interest is compounded four times per year. So in the equation , n = 4.
    ::季度复利意味着利息每年复利四次。在等式中,n=4。

    A ( t ) = P ( 1 + r n ) n t
    ::A(t) = P(1+rn)

    A ( 10 ) = 6000 ( 1 + .025 4 ) 4 ⋅ 10
    ::A(10)=60000(1+.02544)410

    A ( 10 ) = 6000 ( 1.00625 ) 40
    ::A(10)=60000(1.00625)40

    A ( 10 ) = $ 12 , 830.30
    ::A(10)=12 830.30美元

    In each example, the value of the investment after 10 years depends on three quantities: the principal of the investment, the number of compoundings per year, and the interest rate.
    ::在每个例子中,投资10年后的价值取决于三个数量:投资本金、每年增殖次数和利率。

    Example 7
    ::例7

    How long will it take $2000 to grow to $25,000 at a 5% interest rate?
    ::以5%的利率增长到25 000美元需要2 000美元多久?

    It will take about 50 years:
    ::大约需要50年时间:

    A ( t ) = Pe rt  
    25,000 = 2000 e .05(t)  
    12.5 = e .05(t) Divide both sides by 2000
    ln 12.5 = ln e .05( t ) Take the ln of both sides
    ln 12.5 = .05 t ln e Use the power property of logs
    ln 12.5 = .05 t × 1 ln e = 1
    ln 12.5 = 0.5 t Isolate t
    t = l n 12.5 .05 ≈ 50.5  

    Review
    ::回顾

    1. What is the formula for figuring simple interest?
      ::确定简单利息的公式是什么?
    2. What is the formula for figuring compound interest?
      ::确定复合利息的公式是什么?
    3. If someone invested $4500.00, how much would they have earned after 4 years, at a simple interest rate of 2%?
      ::如果有人投资4500.00美元,那么四年后他们能挣多少? 利率只有2%?
    4. Kyle opened up a savings account in July. He deposited $900.00. The bank pays a simple interest rate of 5% annually. What is Kyle's balance at the end of 4 years?
      ::Kyle在7月开了一个储蓄账户,他存了900.00美元。银行每年支付5%的简单利率。四年结束时Kyle的余额是多少?
    5. After having an account for 6 years, how much money does Roberta have in the account, if her original deposit was $11,000, and her bank's yearly simple interest rate is 8.4%?
      ::在拥有一个6年的账户之后,如果Roberta的原始存款为11 000美元,而且她的银行每年的简单利率为8.4%,那么罗贝塔在该账户中有多少钱?
    6. Tom called his bank today to check on his savings account balance. he was surprised to find a balance of $6600, when he started the account with just $5000.00 8 years ago. Based on this data, what percentage rate has the bank been paying on the account?
      ::汤姆今天打电话给他的银行查看他的储蓄账户余额。 他惊讶地发现6600美元的余额,8年前他开户时只有5000.00美元。 根据这个数据,银行在账户上支付的百分比是多少?
    7. Julie opened a 4% interest account with a bank that compounds the interest quarterly. If Julie were to deposit $3000.00 into the account at the beginning of the year, how much could she expect to have at the end of the year?
      ::朱莉在一家银行开了一个4%的利息账户,这家银行每季增加利息。 如果朱莉在年初向该账户存款300美元,那么她在年底能期望多少?
    8. Susan has had a saving account for a few years now. The bank has been paying her simple interest at a rate of 5%. She has earned $45.00 on her initial deposit of $300.00. How long has she had the account?
      ::Susan的储蓄账户已经存了几年了。 银行一直以5%的利率支付她的简单利息。 她的初始存款为300.00美元,挣了45美元。 她有这个账户多久了?
    9. What is the balance on a deposit of $818.00 earning 5% interest compounded semiannually for 5 years?
      ::818.00美元存款的余额是多少? 5年中每半年赚取5%的利息,每半年再加5%。
    10. What is the yearly simple interest rate that Ken earns, if after only three months he earned $16.00 on an initial $800.00 deposit?
      ::Ken每年的简单利率是多少? 如果三个月后,他在最初的800.00美元存款上赚了16美元,那么每年的简单利率是多少?
    11. Write an expression that correctly represents the balance on an account after 7 years, if the account was compounded yearly at a rate of 5%, with an initial balance of $1000.00
      ::写一个表达式,正确代表7年后账户余额的余额,如果账户每年以5%的费率复算,初始余额为1000.00美元,则该表达式在7年后正确代表账户余额。
    12. Caryl gives each of his three kids $3000.00 each, and they each use it to open up a simple interest saving accounts at three different banks. Georgia, his oldest, is earning 3% annually at her bank. Kirk earns 7% annually at his bank. Lottie's bank is paying her an annual rate of 4%. At the end of 6 years show much will each of them have in their respective accounts.
      ::Caryl给三个孩子每人3000.00美元,他们每人用它在三个不同的银行开一个简单的利息储蓄账户。 Georgia,他最年长的乔治亚,每年在她的银行里挣3%。Kirk每年在他的银行里挣7%。Lottie的银行每年付她4%的利率。在6年结束时,每个银行在各自的账户里都有很大的收益。
    13. Kathy receives an inheritance check for $3000.00 and decides to put it in a saving account so she can send her daughter to college when she gets older. After looking she finds an account that pays compounding interest annually at a rate of 14%. The balance on the account can be represented by a function, where x is the time in years. Write a function, and then use it to determine how much will be in the account at the end of 7 years.
      ::Kathy收到一份3000.00美元的继承支票,并决定将支票存入储蓄账户,以便她女儿长大后可以送她上大学。在查看她找到一个每年以14%的利率支付加息的账户。账户余额可以由函数代表,其中x是年中的时间。写一个函数,然后用它来确定在7年结束时该账户的金额。
    14. Stan is late on his car payment. The finance company charges 3% interest per month it is late. His monthly payment is $300.00. What is the total amount he will owe if he pays the August first bill October first? (assuming he was able to make his September bill on - time)
      ::Stan的汽车付款迟了。 金融公司每月收取3%的利息。 他每月的付款为300.00美元。 如果他支付8月10月的10月第一张账单,他将拖欠的总额是多少? (假设他能够按时提出9月的账单)

    Today, you get your first credit card. It charges 12.49% interest on all purchases and compounds that interest monthly. Within one day you max out the credit limit of $1,200.00.
    ::今天,你可以拿到第一张信用卡。它收取12.49%的利息,每月购买和加注利息。在一天之内,你将最多不超过1 200.00美元的信用限额。

    1. If you pay the monthly accrued interest plus $50.00 towards the initial $1,200 amount every month, how much will you still owe at the end of the first 12 months?
      ::如果你每月向最初的1 200美元支付每月累计利息加50美元,那么在头12个月结束时,你还欠了多少钱?
    2. How much will you have paid in total at the end of the year?
      ::到年底你总共要付多少钱?

    You are preparing for retirement. You invest $10,000 for 5 years, in an account that compounds monthly at 12% per year. However, unless this money is in an IRA or other tax-free vehicle, with zero inflation, you also have an annual tax payment of 30% on the earned interest.
    ::您正在准备退休。 您投资了 10,000 美元, 为期五年, 在一个每月12 % 的账户里。 但是, 除非这笔钱是在爱尔兰共和军或其他免税的车辆里, 并且通货膨胀率为零, 否则您每年还得按所得利息缴纳30%的税款 。

    1. How much will you have in 5 years?
      ::5年后你还要多少钱?
    2. Now take into account that the money loses 3% spending value per year due to inflation, how much is what you have saved really worth at the end of the 5 years?
      ::现在考虑到由于通货膨胀,这笔钱每年损失3%的支出价值,在五年结束时,你所节省的钱到底值多少钱?

    Review (Answers)
    ::回顾(答复)

    Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
    ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。