3.13 指数增长

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 指数增长

  Collapse Expand

  指数增长

  播放段落

  Andrew and Kaz have designed a website for fans of their favorite online game "EverStar." The membership started off rather slow, but has been growing at an increasing rate over the last few weeks. Their sign-up records look like this:
  ::Andrew和Kaz为他们最喜欢的在线游戏“EverStar ” 的粉丝设计了一个网站。 会员人数开始相当缓慢,但在过去几周中一直在增长。 他们的注册记录是这样的:

  Week	Members
  1	10
  2	22
  3	48
  4	106
  5	233

  播放段落

  How could Andrew and Kaz write a function to allow them to calculate the projected membership of the website over the next few weeks?
  ::Andrew和Kaz如何写下一个功能, 让他们计算未来几周网站预计成员人数?

  播放段落

  Exponential Growth
  ::指数增长

  播放段落

  In prior lessons, we have explored the application of given to particular questions. In this lesson we will examine the process of deriving a function from observed data, so that we can infer or predict data values that were not or could not be observed.
  ::在以往的教训中,我们探索了特定问题的应用,在这个教训中,我们将研究从观察到的数据中产生函数的过程,以便我们可以推断或预测没有或无法观察到的数据值。

  播放段落

  In general, if you have enough information about a situation, you can write an exponential function to model growth in the situation.
  ::一般来说,如果您掌握了足够的形势信息,您可以写一个指数函数来模拟形势的增长。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a question about the new website of Andrew and Kaz.
  ::之前有人问你 安德鲁和卡兹的新网站

  播放段落

  Andrew and Kaz can model the growth of their site over the next few weeks by using the data they have collected to estimate a weekly growth rate as a percentage of current membership.
  ::Andrew和Kaz可以利用他们收集的数据来估计其每周增长率占目前成员的百分比,以此来模拟其网站在未来几周的增长。

  播放段落

  Based on their current data, their membership is growing at a rate of apx 220% per week. Future membership could therefore be estimated with a function like: $\begin{array}{r}{M}_f=M_i(2.2{)}^t\end{array}$
  ::根据他们目前的数据,他们的会员人数正在以每周220%的apx220%的速度增长。 因此,可以估计未来会员人数,其功能如下:Mf=MI(2.2)t。

  播放段落

  It is important to note that this is only an educated guess, as there will be many many factors which might alter the continued growth of their site!
  ::需要指出的是,这只是一个经过教育的猜测,因为有许多因素可能会改变网站的持续增长。

  播放段落

  Example 2
  ::例2

  播放段落

  A social networking website is started by a group of 10 friends. They advertise their site before they launch, and membership grows fast: the membership doubles every day.
  ::社交网站由十位朋友组成。 他们成立前就刊登网站广告, 会员人数增长很快:会员人数每天翻一番。

  播放段落
  1. Derive an equation to model the growth of the site.
     ::生成一个方程式来模拟网站的生长
  播放段落
  2. At this rate, what will the membership be in a week?
     ::按这个速度,一周后会是什么成员?
  播放段落
  3. When will the membership reach 100,000?
     ::成员何时能达到10万人?

  播放段落

  To model this situation, let’s look at how the membership changes each day:
  ::以这种情形为模范, 让我们看看会籍如何天天改变:

  Time (in days)	Membership
  0	10
  1	2 × 10 = 20
  2	2 × 2 × 10 = 40
  3	2 × 2 × 2 × 10 = 80
  4	2 × 2 × 2 × 2 × 10 = 160

  播放段落

  Notice that the membership on day x is 10(2 ^x ).
  ::通知第x天成员为10(2x)。

  播放段落
  1. We can model membership with the function M ( x ) = 10(2 ^x ).
     ::我们可以以 M(x) = 10(2x) 的功能模拟会员资格。
  播放段落
  2. In seven days, the membership will be M (7) = 10(2 ⁷ ) = 1280.
     ::七天内,成员为M(7)=10(27)=1 280。
  播放段落
  3. We can solve an exponential equation to find out when the membership will reach 100,000:
     ::我们可以解决一个指数式的方程式,

  播放段落

  $\begin{array}{r}10(2^x)=100,000\end{array}$
  ::10(2x)=100 000

  播放段落

  $\begin{array}{r}{2}^x=10,000\end{array}$
  ::2x=10 000

  播放段落

  $\begin{array}{r}log{2}^x=log10,000\end{array}$
  ::log2x=log10 000

  播放段落

  $\begin{array}{r}xlog2=4\end{array}$
  ::xlog2=4

  播放段落

  $\begin{array}{r}x=\frac{4}{log2}\approx 13.3\end{array}$ days.
  ::x=4log213.3天。

  播放段落

  Example 3
  ::例3

  播放段落

  Suppose the membership of the website in "Example 2" grew more reasonably. The new website membership doubles every 7 days.
  ::假设网站的“实例2”成员增加得更合理。 新的网站成员每七天翻一番。

  播放段落
  1. Derive a function to model this growth.
     ::产生一个函数来模拟这种增长。
  播放段落
  2. What would the membership be in 3 months?
     ::3个月内会是什么成员?

  Time (in days)	Membership
  0	10
  7	2 × 10 = 20
  14	2 × 2 × 10 = 40
  21	2 × 2 × 2 × 10 = 80
  28	2 × 2 × 2 × 2 × 10 = 160

  播放段落

  We can no longer use the function M ( x ) = 10(2 ^x ). However, we can use this function to find another function to model this new situation. Looking at one data point will help. Consider for example the fact that M (21) = 10(2 ³ ). This is the case because 21 days results in 3 periods of doubling. In order for x = 21 to produce 2 ³ in the equation, the exponent in the function must be x /7. So we have $\begin{array}{r}M(x)=10\left(2^{\frac{x}{7}}\right)\end{array}$
  ::我们不能再使用 M(x) 函数 = 10( 2x) = 10( 2x) 。 但是, 我们可以使用此函数来找到另一个函数来模拟这一新的情况。 查看一个数据点会有帮助 。 例如, 考虑M( 21) = 10( 23) 。 21天的结果是3个周期翻一番, 情况就是这样 。 为了让 x = 21 生成方程中的 23, 函数的出处必须是 x/7 。 因此, 我们的 M( x) = 10( 2x7) 。

  播放段落

  Let’s verify that this equation makes sense for the data in the table:
  ::让我们验证这个方程式对于表格中的数据是否合理:

  播放段落

  $\begin{array}{r}M(0)=10\left(2^{\frac{0}{7}}\right)=10(1)=10\end{array}$
  ::M(0)=10(207)=10(1)=10

  播放段落

  $\begin{array}{r}M(7)=10\left(2^{\frac{7}{7}}\right)=10(2)=20\end{array}$
  ::M(7)=10(277)=10(2)=20

  播放段落

  $\begin{array}{r}M(14)=10\left(2^{\frac{14}{7}}\right)=10(2^2)=10(4)=40\end{array}$
  ::M(14)=10(2147)=10(22)=10(4)=40

  播放段落

  $\begin{array}{r}M(21)=10\left(2^{\frac{21}{7}}\right)=10(2^3)=10(8)=80\end{array}$
  ::M(21)=10(2217)=10(23)=10(8)=80

  播放段落

  $\begin{array}{r}M(28)=10\left(2^{\frac{28}{7}}\right)=10(2^4)=10(16)=160\end{array}$
  ::M(28)=10(2287)=10(24)=10(16)=160

  播放段落

  Notice that each x value represents one more event of doubling, and in order for the function to have the correct power of 2, the exponent must be ( x /7).
  ::注意每个 x 值代表一个加倍的又一个事件,并且为了使函数具有正确的2的功率,推算方必须是(x/7)。

  播放段落
  1. A function that models the new growth is: $\begin{array}{r}M(x)=10\left(2^{\frac{x}{7}}\right)\end{array}$
     ::函数模型新增长的函数为: M(x)=10(2x7)
  播放段落
  2. The membership reaches 100,000 in about 3 months (93 days):
     ::成员在大约3个月(93天)内达到100 000人:

  播放段落

  $\begin{array}{r}10\left(2^{\frac{x}{7}}\right)=100,000\end{array}$
  ::10(2x7)=100 000

  播放段落

  $\begin{array}{r}{2}^{\frac{x}{7}}=100,000\end{array}$
  ::2x7=100 000

  播放段落

  $\begin{array}{r}log{2}^{\frac{x}{7}}=log100,000\end{array}$
  ::log2x7 = 100,000 log

  播放段落

  $\begin{array}{r}\frac{x}{7}log2=4\end{array}$
  ::x7log2=4

  播放段落

  $\begin{array}{r}xlog2=28\end{array}$
  ::xlog2=28

  播放段落

  $\begin{array}{r}x=\frac{28}{log2}\approx 93\end{array}$
  ::x=28log293

  播放段落

  Example 4
  ::例4

  播放段落

  The population of a town was 20,000 in 1990. Because of its proximity to technology companies, the population grew to 35,000 by the year 2000.
  ::1990年,一个城镇的人口为20,000人,由于靠近技术公司,到2000年,人口增至35,000人。

  播放段落
  1. Derive an equation to model the described growth rate.
     ::产生一个方程式来模拟所描述的增长率。
  播放段落
  2. If the growth continues at this rate, how long will it take for the population to reach 1 million?
     ::如果增长率继续以这种速度增长,人口达到100万需要多长时间?

  播放段落

  The general form of the exponential growth model is much like the continuous compounding function you learned in the previous lesson. We can model exponential growth with a function of the form P (t) = P ₀ e ^kt . The expression P ( t ) represents the population after t years, the coefficient P ₀ represents the initial population, and k is a growth constant that depends on the particular situation.
  ::指数增长模型的一般形式与您在上一课中所学到的连续复合函数非常相似。 我们可以用表P(t) = P0ekt 的函数来模拟指数增长。 表达式P(t) 代表 T 年之后的人口, 系数P0 代表初始人口, k 是一个增长常数, 取决于具体情况 。

  播放段落

  In the situation above, we know that P ₀ = 20,000 and that P (10) = 35,000. We can use this information to find the value of k :
  ::在上述情况下,我们知道P0=20 000,P(10)=35 000。

  播放段落

  $\begin{array}{r}P(t)=P_0{e}^{kt}\end{array}$
  ::P(t) = P0ekt

  播放段落

  $\begin{array}{r}P(10)=35000=20,000e^{k\cdot 10}\end{array}$
  ::P(10)=35000=20,000ek10

  播放段落

  $\begin{array}{r}\frac{35,000}{20,000}=e^{10k}\end{array}$
  ::355,520,000=e10k

  播放段落

  $\begin{array}{r}1.75=e^{10k}\end{array}$
  ::1.75=e10k

  播放段落

  $\begin{array}{r}ln1.75=ln{e}^{10k}\end{array}$
  ::In 1. 75=lne10k (lne10k)

  播放段落

  $\begin{array}{r}ln1.75=10klne\end{array}$
  ::IN1.75=10klne( 10klne)

  播放段落

  $\begin{array}{r}ln1.75=10k(1)\end{array}$
  ::IN1.75=10k(1)

  播放段落

  $\begin{array}{r}ln1.75=10k\end{array}$
  ::In. 1. 75=10k

  播放段落

  $\begin{array}{r}k=\frac{ln1.75}{10}\approx 0.056\end{array}$
  ::k=001. 7510 0.056

  播放段落
  1. We can model the population growth with the function $\begin{array}{r}P(t)=20,000e^{\frac{ln1.75}{10}t}\end{array}$ .
     ::我们可以以 P(t) = 20,000 eln1.7510t 的功能来模拟人口增长。
  播放段落
  2. We can determine when the population will reach 1,000,000 by solving an equation, or using a graph.
     ::我们可以通过解答方程式或使用图表来决定人口何时会达到1 000 000人。

  播放段落

  Using an equation:
  ::使用方程式 :

  播放段落

  $\begin{array}{r}1,000,000=20,000e^{\frac{ln1.75}{10}t}\end{array}$
  ::1 000 000=20 000 eln1.7510t

  播放段落

  $\begin{array}{r}50=e^{\frac{ln1.75}{10}t}\end{array}$
  ::50=eln1.7510t

  播放段落

  $\begin{array}{r}ln50=ln\left(e^{\frac{ln1.75}{10}t}\right)\end{array}$
  ::In50=ln( eln1. 7510t)

  播放段落

  $\begin{array}{r}ln50=\frac{ln1.75}{10}t(lne)\end{array}$
  ::In50 = 0. 7510t( lne)

  播放段落

  $\begin{array}{r}ln50=\frac{ln1.75}{10}t(1)\end{array}$
  ::IN50=1.7510t(1)

  播放段落

  $\begin{array}{r}10ln50=ln1.75t\end{array}$
  ::10n50 = 1. 75t

  播放段落

  $\begin{array}{r}t=\frac{10ln50}{ln1.75}\approx 70\end{array}$
  ::t = 10ln50ln1.7570

  播放段落

  At this rate, it would take about 70 years for the population to reach 1 million.
  ::按此速度计算,人口达到100万将需要70年左右的时间。

  播放段落

  Example 5
  ::例5

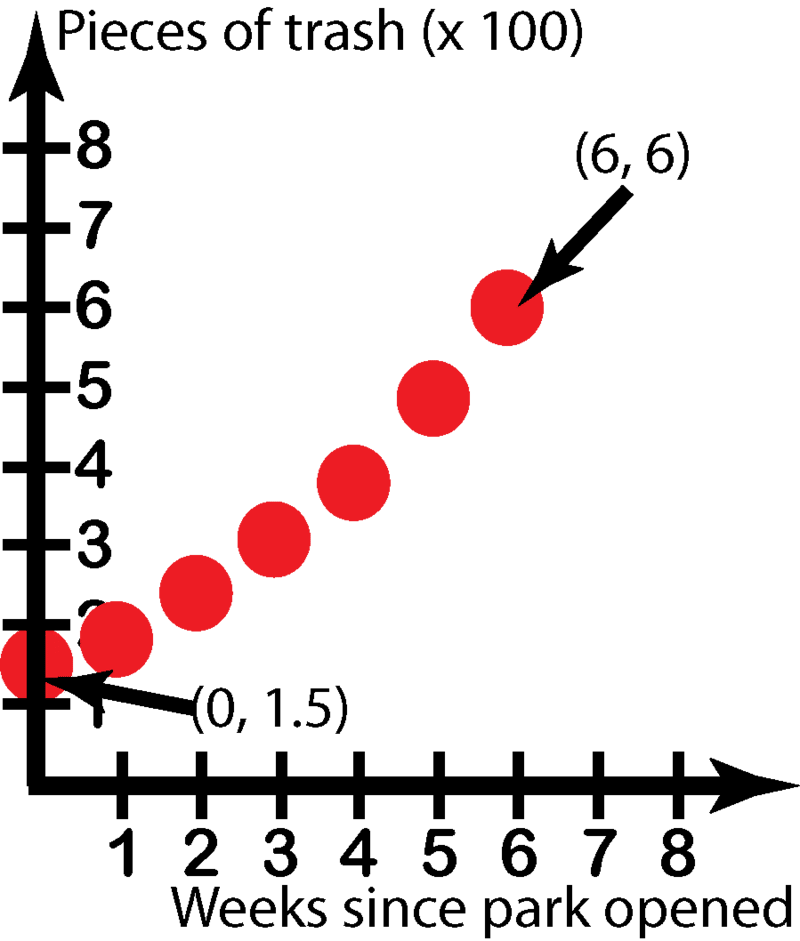
  播放段落

  You are presented with data collected from a National Forest Campground. According to the ranger who provided it, the number of pieces of garbage found in the park has been increasing exponentially during the year as the summer season approaches. Using the data points on the graph below, derive an exponential equation which describes the data.
  ::向您展示了从国家森林营地收集的数据。 根据提供这些数据的护林员,随着夏季的临近,该公园中发现的垃圾数量在这一年中呈指数式增长。使用下图的数据点,得出一个指数式方程式来描述数据。

  

  播放段落

  To find the equation of the line of an exponential equation from specific points, we can use the "base-intercept" form: $\begin{array}{r}y=P_0(a^x)\end{array}$ where $\begin{array}{r}{P}_0\end{array}$ is the y-coordinate of our starting value, assuming that to also be x = 0 (the starting time).
  ::要从特定点找到指数方程的方程式, 我们可以使用“ 基准截取” 格式: y=P0( 轴) , P0 是我们起始值的 Y 坐标, 假设也为 x = 0( 起始时间 ) 。

  播放段落

  Start by finding the base a with: $\begin{array}{r}a=(\frac{y_2}{y_1}{)}^{\frac{1}{x_2-x_1}}\end{array}$
  ::以查找基底为 a 开始: a= (y2y1) 1x2- x1

  播放段落

  $\begin{array}{r}a=(\frac{6}{1.5}{)}^{\frac{1}{6-0}}\end{array}$ : using the data from the first and last points on the graph
  ::a=(61.5)16-0:使用图中第一个和最后一个点的数据。

  播放段落

  $\begin{array}{r}a=4^{\frac{1}{6}}\end{array}$
  ::a=416

  播放段落

  $\begin{array}{r}a=1.259921\end{array}$
  ::a=1.259921

  播放段落

  Substitute the new value for a into the base- intercept form :
  ::替换 ain 的 新值 :

  播放段落

  $\begin{array}{r}y=1.5({1.259921}^x)\end{array}$
  ::y=1.5(1.259921x)

  播放段落

  $\begin{array}{r}\therefore y=1.5({1.259921}^x)\end{array}$ is the equation for estimating the number of pieces of trash (in hundreds) in any given week.
  ::y=1.5(1.259921x)是估算任何特定星期垃圾件数(以百计)的方程式。

  播放段落

  Review
  ::回顾

  播放段落

  Write an exponential function to model the situation.
  ::写入指数函数以模拟情况。

  播放段落
  1. Your salary of $35,000 increases 8% each year.
     ::你35,000美元的工资每年增加8%
  播放段落
  2. A population of 300,000 increases by 12% each year.
     ::300,000人口每年增加12%。
  播放段落
  3. A business had a $23,000 profit in 2009. Then the profit increased by 20% per year for the next 5 years.
     ::一个企业2009年的利润为23 000美元,随后在未来5年内每年利润增加20%。

  播放段落

  Answer the questions about the given investment.
  ::回答关于特定投资的问题。

  播放段落
  4. What is the balance after 7 years if you deposit $2800 in an account that pays 4% interest compounded yearly?
     ::7年后的余额是多少? 如果你把2800美元存入一个每年支付4%利息的账户里?
  播放段落
  5. What is the balance after 3 years if you deposit $3500 in an account that pays 2% interest compounded yearly?
     ::3年后的余额是多少? 如果你把3500美元存入一个每年支付2%利息的账户里?
  播放段落
  6. What is the balance after 15 years if you deposit $1800 in an account that pays 8% interest compounded quarterly?
     ::15年后的余额是多少? 如果你把1800美元存入一个每季度支付8%利息的账户?

  播放段落

  The property value on a specific block in a large city grows exponentially every year. In the year 2011, you purchased a piece of property on this block. The table below represents the value of the property you purchased each year since 2006
  ::大城市特定区块的地产价值每年以指数指数增长。2011年,您在这一区块上购买了一块地产。下表显示了2006年以来每年购买的财产价值。

  Year	Value
  2006	$379,786
  2007	$401,259
  2008	$423,946
  2009	$447,917
  2010	$473,242
  2011	$500,000

  播放段落

  Use this data for questions 7-10:
  ::将这些数据用于问题7-10:

  播放段落
  7. By what percentage is the price of the property in this block increasing per year?
     ::这个区块的财产价格每年以多少百分比增长?
  播放段落
  8. Derive the function to model the growth of the value of the property.
     ::生成函数以模拟财产价值的增长。
  播放段落
  9. What will the property be worth in the year 2020?
     ::2020年该地产值多少?
  播放段落
  10. When will the property be worth 750 thousand dollars?
      ::财产什么时候会值七十五万美元?
  播放段落
  11. In 1995, the world’s population was 5.7 billion and was growing at a relative rate of 2% per year. Find the population of the world in the year 2020
      ::1995年,世界人口为57亿,每年以2%的相对增长率增长。 2020年,世界人口将达到2 % 。
  播放段落
  12. You are working with a bacteria that doubles in cellular quantity every thirty minutes. If the initial population of the bacteria is 95, what is the population of bacteria a) After three hours? b) After one day?
      ::如果最初的细菌数量是95,那么3小时之后的细菌数量是多少? (b)一天之后?
  播放段落
  13. After losing your job, and needing cash fast, you decide to try your hand at gambling. This turns out to be a terrible decision on your part, as you lose more money and in fact end up owing the casino. At an interest rate of 22% per year, how much will you owe on a loan of $4,000: a)after one year? b)after three years?
      ::失去工作后,需要快速现金,你决定尝试赌博。这实际上对你来说是一个可怕的决定,因为你损失了更多的钱,实际上还欠了赌场。 年利率为22%,4000美元的贷款需要多少钱? 一年之后? (b)三年后?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。