课程： 4.1 极坐标 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节极地坐标

折叠展开
极地坐标
Everyone has dreamed of flying at one time or another. Not only would there be much less traffic to worry about, but directions would be so much simpler!
::每个人都梦想在某个时候飞翔,不仅需要担心的交通量要少得多,而且方向要简单得多!

Walking or driving: "Go East 2 blocks, turn left, then North 6 blocks. Wait for the train. Turn right, East 3 more blocks, careful of the cow! Turn left, go North 4 more blocks and park."
::步行或驾驶:“往东走2个街区,向左转,然后向北走6个街区。等待火车。右转,往东走3个街区,小心牛!左转,往北走4个街区和公园。”

Flying: "Fly 30 deg East of North for a little less than 11 and 1/4 blocks. Land."
::飞行:"北面以东飞行30度, 飞行区小于11和14个街区,陆地"

Nice daydream, but what does it have to do with ?
::做白日梦不错,但又有什么关系呢?

Polar Coordinates
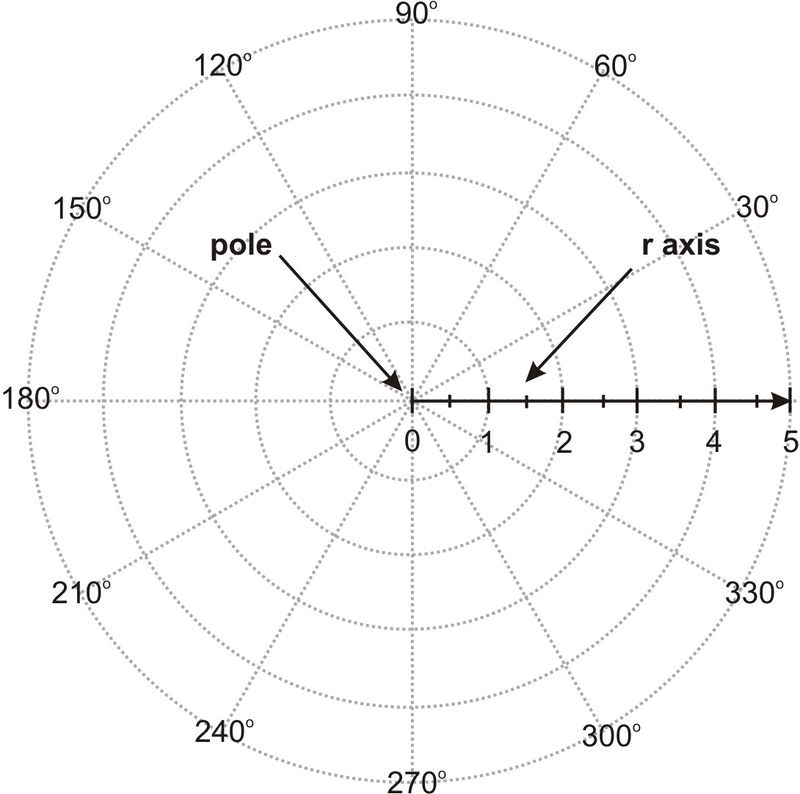
::极地坐标

The polar coordinate system is an alternative to the Cartesian coordinate system you have used in the past to graph functions. The polar coordinate system is specialized for visualizing and manipulating angles.
::极地坐标系统是您过去用于图形函数的笛卡尔坐标系统的一种替代。极地坐标系统专门用于可视化和操纵角度。

Angles are identified by travelling counter-clockwise around the circular graph from the 0 deg line, or r-axis (where the + x axis would be) to a specified angle.
::通过逆时针绕圆形图从 0 deg 线或 r 轴(即 + x 轴的位置) 绕圆形图到指定角进行反时针飞行来识别角。

To plot a specific point, first go along the r -axis by r units. Then, rotate counterclockwise by the given angle, commonly represented "θ". Be careful to use the correct units for the angle measure (either radians or degrees).
::要绘制一个特定点, 请先用 r 单位沿 r 轴沿 r 轴。然后, 以给定角度逆时针旋转, 通常表示“ {} ” 。注意使用正确的单位来测量角( 弧度或度) 。

Radians
::弧度

Usually polar plots are done with radians (especially if they include trigonometric functions), but sometimes degrees are used.
::极地通常使用弧度(特别是如果包括三角函数),但有时使用度。

A radian is the angle formed between the r axis and a polar axis drawn to meet a section of the circumference that is the same length as the radius of a circle.
::弧度是指圆轴与极轴之间形成角,以便与圆圆半径相同长度的环绕部分相匹配。

Given that the circumference of a circle is $\begin{aligned} 2 π \cdot r \end{aligned}$ , and since r is the radius, that means there are $\begin{aligned} 2 π \end{aligned}$ radians in a complete circle, and $\begin{aligned} 1 π \end{aligned}$ radians in 1/2 of a circle.
::鉴于圆环的周长是 2 ° r ,而且由于 r 是半径,这意味着整个圆的弧度是 2 ;圆的弧度是 1/2 。

If 1/2 of a circle is $\begin{aligned} π \end{aligned}$ radians, and is 180 deg, that means that there are $\begin{aligned} \frac{180}{π} \end{aligned}$ degrees in each radian.
::如果圆1/2是弧度,为180度,则每个弧度为180°。

That translates to approximately 57.3 degrees = 1 radian.
::相当于约57.3度=1弧度。

Graphing Using Technology
::利用技术图图绘制图图

Polar equations can be graphed using a graphing calculator: With the graphing calculator- go to MODE . There select RADIAN for the angle measure and POL (for Polar) on the FUNC (function)line. When Y = is pressed, note that the equation has changed from y = to r = . There input the polar equation. After pressing graph, if you can’t see the full graph, adjust x - and y - max/min, etc in WINDOW.
::极方程式可以用图形计算器绘制图解: 图形计算器- 转到 MODE 。在 FUNC( 函数) 线上选择角度量的 RADIAN 和 POL( 用于极地) 。当 Y = 按下时, 注意方程式已经从 y = 改为 r = 。在按下图后, 输入极方方程式。如果您在 WINDOW 中看不到整图, 请调整 x 和 y 最大/ min 等。

Examples
::实例

Example 1
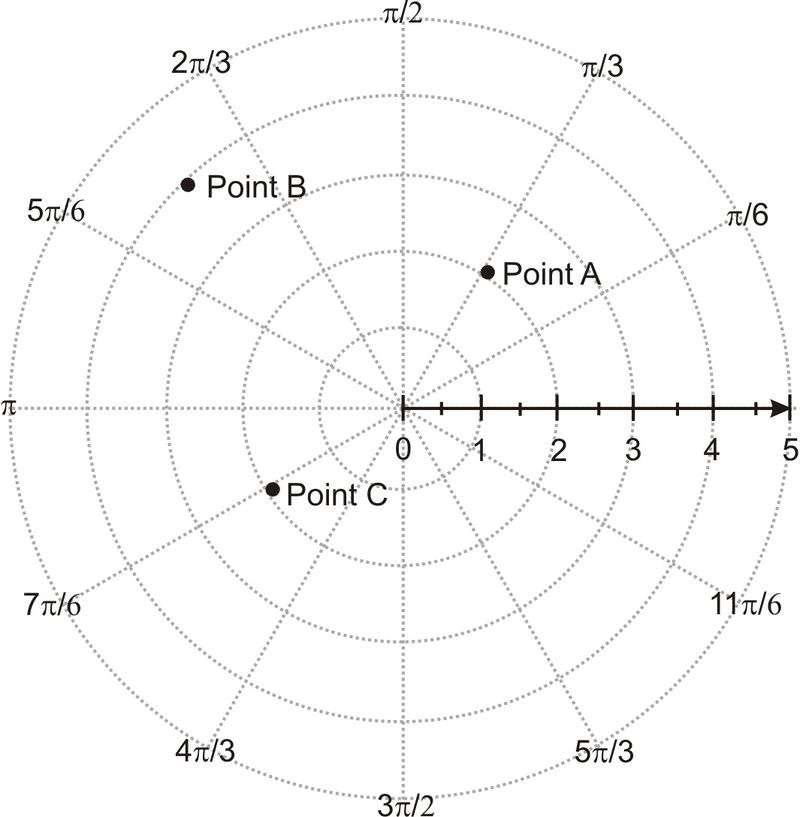
::例1

Plot the points on a polar coordinate graph: Point A $\begin{aligned} (2, \frac{π}{3}) \end{aligned}$ , Point B $\begin{aligned} (4, 135^{o}) \end{aligned}$ , and Point C $\begin{aligned} (- 2, \frac{π}{6}) \end{aligned}$ .
::在极地坐标图上绘制点数:A点(2 3)、B点(4 135o)和C点(-2 6)。

Below is the pole, polar axis and the points A, B and C.
::下面是极、极轴和A、B和C点。

Example 2
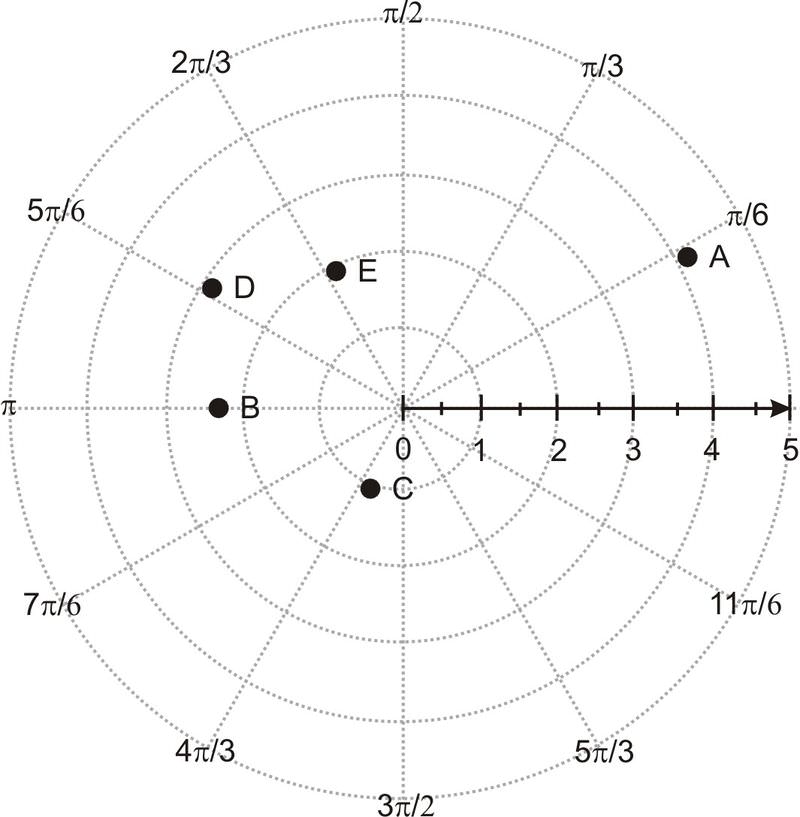
::例2

Plot the following points.
::绘制以下各点。

$\begin{aligned} (4, 30^{o}) \end{aligned}$
:4,30o)

$\begin{aligned} (2.5, π) \end{aligned}$

$\begin{aligned} (- 1, \frac{π}{3}) \end{aligned}$

$\begin{aligned} (3, \frac{5 π}{6}) \end{aligned}$

$\begin{aligned} (- 2, 300^{o}) \end{aligned}$
:-2,300,300o)

Example 3
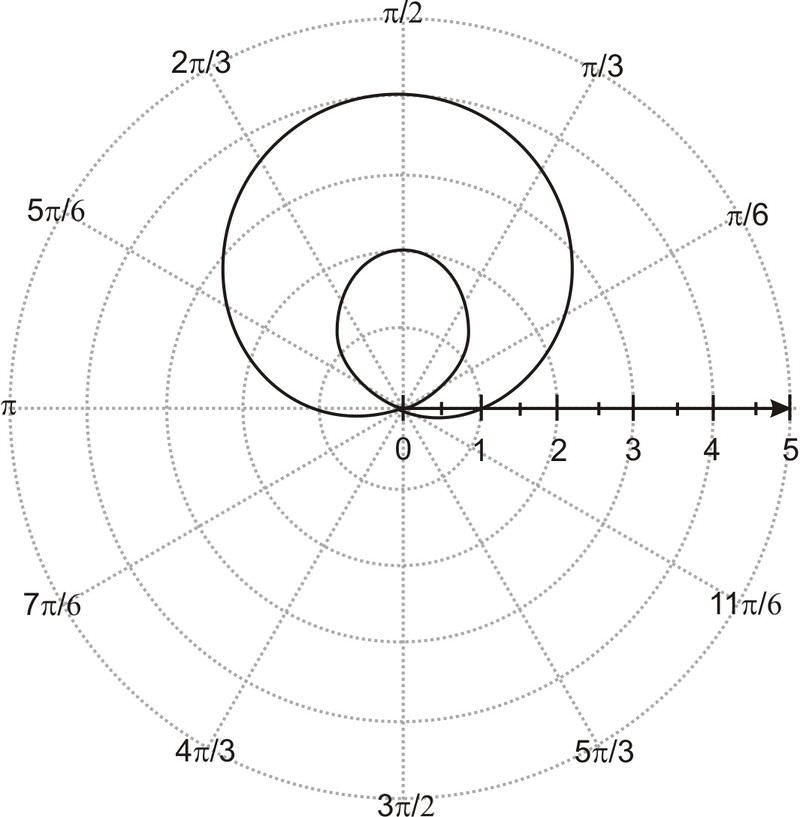
::例3

Use a graphing calculator or plotting program to plot the following equations.
::使用图形计算器或绘图程序绘制以下方程式。

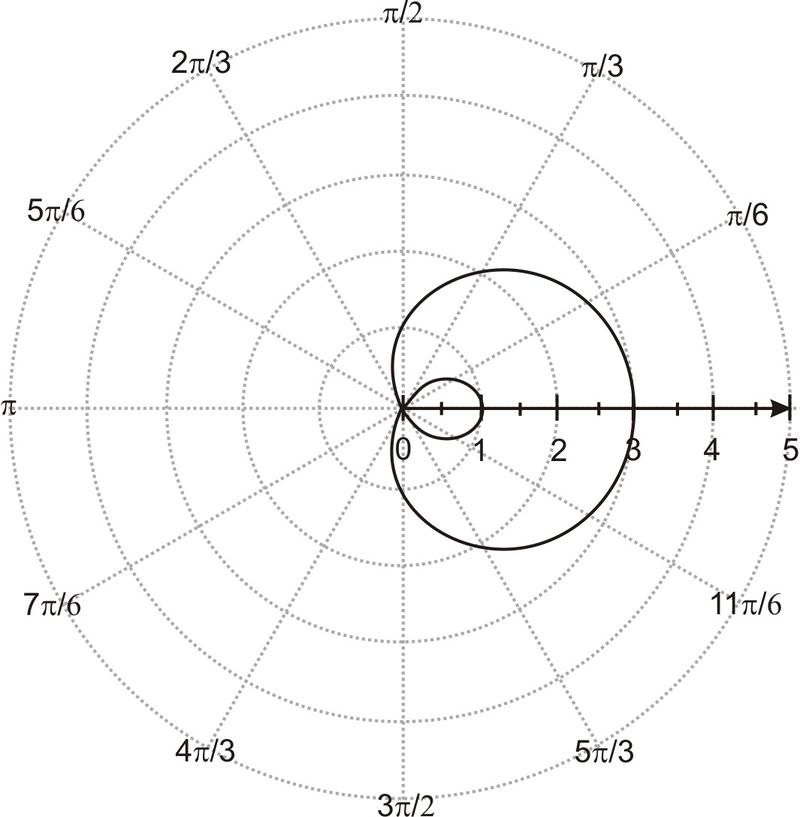
$\begin{aligned} r = 1 + 3 s i n θ \end{aligned}$
::r=1+3sin

$\begin{aligned} r = 1 + 2 c o s θ \end{aligned}$
::r=1+2cos

Review the steps above under graphing using technology if you are having trouble.
::若您遇到问题,请在使用技术绘制图图时审查上述步骤。

Example 4
::例4

Convert from radians to degrees.
::将弧度转换为度。

Recall that $\begin{aligned} π r a d = 180^{o} \end{aligned}$ and $\begin{aligned} 1 r a d = \frac{180}{π} \approx {57.3}^{o} \end{aligned}$ .
::回想一下:180oand1rad=18057.3o。

$\begin{aligned} \frac{π}{2} \end{aligned}$

If $\begin{aligned} π r a d = 180^{o} \end{aligned}$ then $\begin{aligned} \frac{π}{2} r a d = 90^{o} \end{aligned}$
::若变差=180othen=90o

$\begin{aligned} 5.17 \end{aligned}$

If $\begin{aligned} 1 r a d \approx {57.3}^{o} \end{aligned}$ then $\begin{aligned} 5.17 r a d \approx 296^{o} \end{aligned}$
::如果1rad=57.3othen5.17rad=296o

$\begin{aligned} \frac{3 π}{2} \end{aligned}$

If $\begin{aligned} π r a d = 180^{o} \end{aligned}$ then $\begin{aligned} \frac{3 π}{2} r a d = 270^{o} \end{aligned}$
::如果功=180othen32rad=270o

Example 5
::例5

Convert from degrees to radians.
::将度转换为弧度。

Recall that $\begin{aligned} \frac{180^{o}}{π} = {57.3}^{o} \approx 1 r a d \end{aligned}$ .
::回忆到: 180o57.3o1rad。

$\begin{aligned} 251^{o} \end{aligned}$
::251o

If $\begin{aligned} {57.3}^{o} \approx 1 r a d \end{aligned}$ then $\begin{aligned} 251^{o} \approx 4.38 r a d \approx 1.4 π r a d \end{aligned}$
::如果57.3o=1radthen251o=4.38rad=1.4rad

$\begin{aligned} 360^{o} \end{aligned}$
::360o

If $\begin{aligned} {57.3}^{o} \approx 1 r a d \end{aligned}$ then $\begin{aligned} 360^{o} \approx 6.28 r a d \end{aligned}$
::如果是57.3o=1radthen360o=6.28rad

$\begin{aligned} 327^{o} \end{aligned}$
::327o

If $\begin{aligned} {57.3}^{o} \approx 1 r a d \end{aligned}$ then $\begin{aligned} \frac{327^{o}}{{57.3}^{o}} \approx 5.71 r a d \end{aligned}$
::如果57.3o=1radthen327o57.3o5.71rad

Example 6
::例6

Convert from degrees to radians, answer in terms of $\begin{aligned} π \end{aligned}$ .
::将度转换为弧度,回答为 °。

Recall that $\begin{aligned} 2 π r a d = 360^{o} \end{aligned}$ and therefore $\begin{aligned} π r a d = 180^{o} \end{aligned}$ .
::回顾2rad=360o,因此rad=180o。

$\begin{aligned} 90^{o} \end{aligned}$
::90o

If $\begin{aligned} π r a d = 180^{o} \end{aligned}$ then $\begin{aligned} \frac{π}{2} r a d = 90^{o} \end{aligned}$
::若变差=180othen=90o

$\begin{aligned} 270^{o} \end{aligned}$
::270o

If $\begin{aligned} π r a d = 180^{o} \end{aligned}$ and $\begin{aligned} \frac{π}{2} r a d = 90^{o} \end{aligned}$ then $\begin{aligned} 1 \frac{1}{2} π r a d \to \frac{3}{2} π \to \frac{3 π}{2} r a d = 270^{o} \end{aligned}$
::如果拉德=180oand2rad=90othen1112332rad=270o

$\begin{aligned} 45^{o} \end{aligned}$
::45o 45o

If $\begin{aligned} \frac{π}{2} r a d = 90^{o} \end{aligned}$ then $\begin{aligned} \frac{π}{4} r a d = 45^{o} \end{aligned}$
::If... 2rad=90othen...4rad=45o

Review
::回顾

Why can a point on the plane not be labeled using a unique ordered pair $\begin{aligned} (r, θ) \end{aligned}$ .
::为何不能使用独家定购的一对(r,______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Explain how to graph $\begin{aligned} (r, θ) \end{aligned}$ if $\begin{aligned} r < 0 \end{aligned}$ and/or $\begin{aligned} θ > 360 \end{aligned}$ .
::如果 r < 0 和/或 360 , 请解释如何图形(r, ) 。

Graph each point on the polar plane.
::绘制极地平面上每一点的图表。

A $\begin{aligned} (6, 145^{o}) \end{aligned}$
::A(6 145o)

B $\begin{aligned} (2, \frac{13 π}{6}) \end{aligned}$
::B(2,136)

C $\begin{aligned} (\frac{7}{4}, - 210^{o}) \end{aligned}$
::C(74,-210o)

D $\begin{aligned} (5, \frac{π}{2}) \end{aligned}$
::D(52美元)

E $\begin{aligned} (3.5, \frac{- π}{8}) \end{aligned}$
::E(3.5,8)

Name two other pairs of polar coordinates for each point.
::每点指定另外两对极坐标。

$\begin{aligned} (1.5, 170^{o}) \end{aligned}$
:1.5,170o)

$\begin{aligned} (- 5, \frac{π}{- 3}) \end{aligned}$

$\begin{aligned} (3, 305^{o}) \end{aligned}$
:3,305o)

Graph each polar equation.
::绘制每一极方程的图解。

$\begin{aligned} r = 3 \end{aligned}$
::r=3

$\begin{aligned} θ = \frac{π}{5} \end{aligned}$

$\begin{aligned} r = 15.5 \end{aligned}$
::r=15.5

$\begin{aligned} r = 1.5 \end{aligned}$
::r=1.5

$\begin{aligned} θ = - 175^{o} \end{aligned}$
::175o

Find the distance between the given points.
::查找给定点之间的距离。

$\begin{aligned} P_{1} (5, \frac{π}{2}) \end{aligned}$ and $\begin{aligned} P_{2} (7, \frac{3 π}{9}) \end{aligned}$
::P1(5,第2,第2,第5,第2,和第2,第7,第3,第9段)

$\begin{aligned} P_{1} (1.3, - 52^{o}) \end{aligned}$ and $\begin{aligned} P_{2} (- 13.6, - 162^{o}) \end{aligned}$
::P1(1.3,-52o)和P2(2-13.6,-162o)

$\begin{aligned} P_{1} (3, 250^{o}) \end{aligned}$ and $\begin{aligned} P_{2} (7, 90^{o}) \end{aligned}$
::P1(3,250o)和P2(7,90o)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

极地坐标

Polar Coordinates ::极地坐标

Radians ::弧度

Graphing Using Technology ::利用技术图图绘制图图

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Polar Coordinates
::极地坐标

Radians
::弧度

Graphing Using Technology
::利用技术图图绘制图图

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)