课程： 4.2 极地和笛卡尔转变

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节极地和笛卡尔转变

折叠展开
极地和笛卡尔转变
You will see during this lesson that points can be converted from rectangular form to polar form with a little algebra and trigonometry.
::您可以在此课中看到, 点可以从矩形形式转换为极形, 使用一点代数和三角测量法。

Can the equation of a shape be converted also? How about a circle, for instance?
::形状的方程式也可以转换吗? 例如圆形如何?

Polar and Cartesian Transformation
::极地和笛卡尔转变

Polar Form to Rectangular Form
::极表到矩形表

Sometimes a problem will be given with coordinates in polar form but rectangular form may be needed.
::有时会有极地坐标问题,但可能需要矩形坐标。

To transform the polar point $\begin{aligned} (4, \frac{3 π}{4}) \end{aligned}$ into rectangular coordinates: first identify (r, θ).
::将极点(4,34)转换成矩形坐标:首先识别(r, )。

r = 4 and $\begin{aligned} θ = \frac{3 π}{4} \end{aligned}$ .
::r = 4 和 34。

Second, draw a vertical line from the point to the polar axis (the horizontal axis). The distance from the pole to where the line you just drew intersects the polar axis is the x value, and the length of the line segment from the point to the polar axis is the y value.
::第二,从点到极轴(水平轴)绘制一条垂直线。从极线到您刚才所画的线交叉的极轴的距离是 x 值,从点到极轴的线段长度是 y 值。

These distances can be calculated using trigonometry:
::这些距离可以用三角测量法计算:

x = r θ and y = r θ
::x = r = r = y = r = r = r =

$\begin{aligned} x = 4 cos \frac{3 π}{4} \end{aligned}$ and $\begin{aligned} y = 4 sin \frac{3 π}{4} \end{aligned}$ or $\begin{aligned} x = - 2 \sqrt{2} y = 2 \sqrt{2} \end{aligned}$
::x=4 34 y=4 34 或 x22 Y=22

$\begin{aligned} (4, \frac{3 π}{4}) \end{aligned}$ in is equivalent to $\begin{aligned} (- 2 \sqrt{2}, 2 \sqrt{2}) \end{aligned}$ in rectangular coordinates.
::矩形坐标(4,34)等于(-22,22)。

Rectangular Form to Polar Form
::矩形窗体到极形的矩形窗体

Going from rectangular coordinates to polar coordinates is also possible, but it takes a bit more work. Suppose we want to find the polar coordinates of the rectangular point (2, 2). To begin doing this operation, the distance that the point (2, 2) is from the origin (the radius, r ) can be found by
::从矩形坐标向极地坐标从矩形坐标到极地坐标也是可能的,但还需要多做一点工作。假设我们想找到矩形点的极坐标(2, 2) 。开始此操作时, 点(2, 2) 与原点( 半径, r) 的距离( 半径, r) 可以通过

$\begin{aligned} r = \sqrt{x^{2} + y^{2}} \end{aligned}$
::r= rx2+y2

$\begin{aligned} r = \sqrt{2^{2} + 2^{2}} \end{aligned}$
::r=22+22

$\begin{aligned} r = \sqrt{8} = 2 \sqrt{2} \end{aligned}$
::r=8=22

The angle that the line segment between the point and the origin can be found by
::点和起源点之间的线段角, 由

$\begin{aligned} tan θ = \frac{y}{x} \end{aligned}$
::晒黑 *yx

$\begin{aligned} tan θ = \frac{2}{2} \end{aligned}$
::丹丹 22

$\begin{aligned} tan θ = 1 \end{aligned}$
::晒黑 #% 1

$\begin{aligned} θ = {tan}^{- 1} 1 \end{aligned}$
::~ 坦 - 11 ~ 坦 - 塔 - 11 ~ 坦 - 塔 - 11 ~ 塔 - 塔 - 11 ~ 塔 - 塔 - 11 ~ 塔 - 塔 - 11 ~ 塔 - 塔 - 11 ~ 塔 - 塔 - 塔 - 11 ~ 塔 - 塔 - 塔 - 塔 - 11 ~ 塔 - 塔 - 塔 - 塔 - 塔 - 塔 - 11

$\begin{aligned} θ = \frac{π}{4} \end{aligned}$

Since this point is in the first quadrant (both the x and y coordinate are positive) the angle must be 45 ^o or $\begin{aligned} \frac{π}{4} \end{aligned}$ radians. It is also possible that when θ = 1 the angle can be in the third quadrant, or $\begin{aligned} \frac{5 π}{4} \end{aligned}$ radians. But this angle will not satisfy the conditions of the problem, since a third quadrant angle must have both x and y negative.
::由于此点位于第一个象限( x 和 y 坐标均为正) , 角度必须是 45 o 或 + 4 弧度。当 = = 1 时, 角度也可以在第三个象限中, 或 5 4 弧度中。但是, 这个角无法满足问题的条件, 因为第三个象限角度必须具有 x 和 y 负。

Note: when using $\begin{aligned} tan θ = \frac{y}{x} \end{aligned}$ to find the measure of θ you should consider, at first, the quotient $\begin{aligned} tan θ = | \frac{y}{x} | \end{aligned}$ and find the first quadrant angle that satisfies this condition. This angle will be called the reference angle , denoted θ _ref . Find the actual angle by analyzing which quadrant the angle must be given the signs of x and y .
::注意 : 当使用 tan yx 来查找的度量时, 您应该首先考虑 tan , 并找到第一个满足此条件的象方角。这个角度将被称为参考角 , 表示 ref 。通过分析 x 和 y 的标记, 找到实际角度。

Examples
::实例

Example 1
::例1

Earlier, you were asked if the equation of a circle could be converted from rectangular form to polar form.
::早些时候,有人问您是否可将圆形的方程从矩形转换为极形。

Equation of a circle: x ² + y ² = k ² is the equation of a circle with a radius of k in rectangular coordinates.
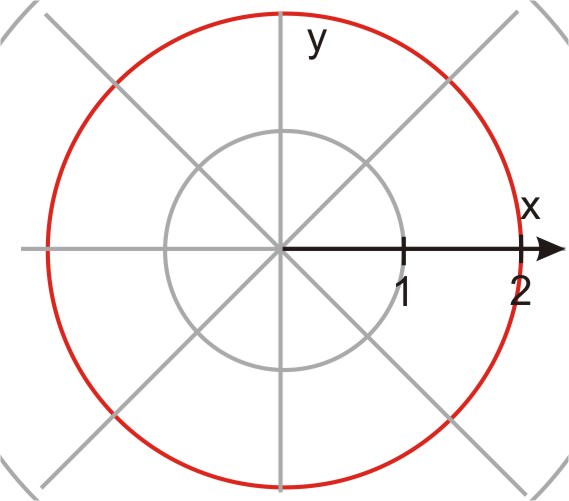
::圆的方程式: x2 + y2 = k2 是圆的方程式,方形坐标为 k 半径。

The equation of a circle is extremely simple in polar form. In fact, a circle on a polar graph is analogous to a horizontal line on a rectangular graph!
::圆形的方程式以极的形式非常简单。事实上, 极图上的圆形类似于矩形图上的水平线 !

You can transform this equation to polar form by substituting the polar values for x , y . Recall x = r cos θ and y = r sin θ .
::您可以用 X , y. recall x = r cos 和 y = r sin 来替换极值, 将这个方程式转换为极形。

( r cos θ ) ² + ( r sin θ ) ² = k ² ,
:r cos )2 + (r sin )2 = k2,

square the terms: r ² cos ² θ + r ² sin ² θ = k ² ,
::平方条件: r2 cs2 + r2 sin2 = k2,

factor the r ² from both terms on the left: r ² (cos ² θ + sin ² θ ) = k ²
::左边两个条件的 r2 系数: r2 (cos2+ sin2) = k2

recall the identity : cos ² θ + sin ² θ = 1
::恢复身份: COS2+ sin2=1

r ² = k ²
::r2 = k2

Therefore: $\begin{aligned} r = \pm k \end{aligned}$ is an equation for a circle in polar units.
::因此:rk是极地单位圆形的方程式。

When r is equal to a constant, the polar graph is a circle.
::当 r 等于常数时,极图是一个圆。

Example 2
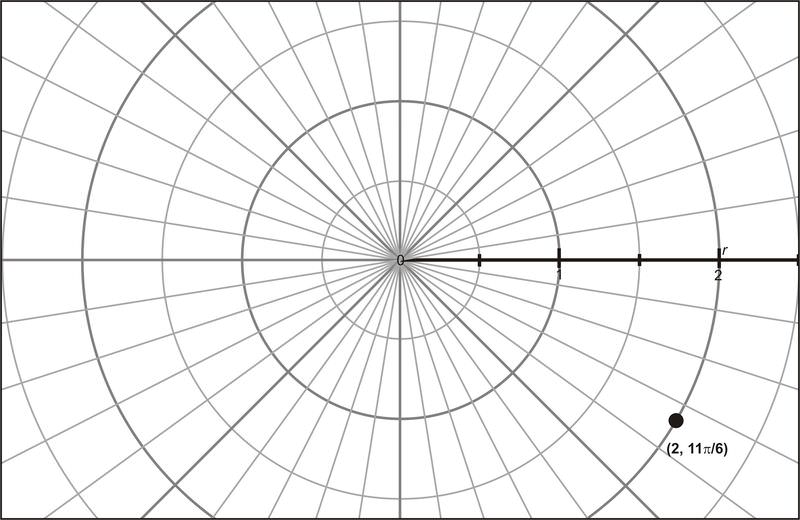
::例2

Transform the polar coordinates $\begin{aligned} (2, \frac{11 π}{6}) \end{aligned}$ to rectangular form.
::将极坐标(2,116)转换为矩形。

$\begin{aligned} r = 2 \end{aligned}$ and $\begin{aligned} θ = \frac{11 π}{6} \end{aligned}$
::r=2和116

$\begin{aligned} x = r cos θ \end{aligned}$ and $\begin{aligned} y = r sin θ \end{aligned}$
::x=r cos 和y=r sin

$\begin{aligned} x = 2 cos \frac{11 π}{6} \end{aligned}$ and $\begin{aligned} y = 2 sin \frac{11 π}{6} \end{aligned}$ or $\begin{aligned} x = 3 \sqrt{2} y = - 1 \end{aligned}$
::x=2 cs 116 and y=2 sin 116 or x=32 y1

$\begin{aligned} (2, \frac{11 π}{6}) \end{aligned}$ is equivalent to $\begin{aligned} (3 \sqrt{2}, - 1) \end{aligned}$ or in decimal form, approximately $\begin{aligned} (4.342, - 1) \end{aligned}$ .
:2,116)相当于(32,-1)或小数点(约4.342,-1),或小数点(约4.342,-1)。

Example 3
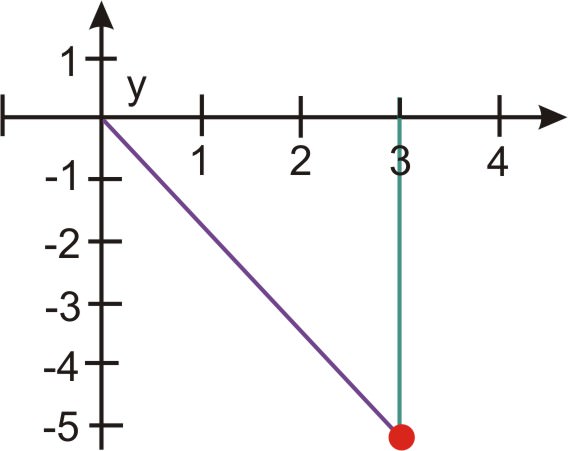
::例3

Find the polar coordinates for $\begin{aligned} (3, - 3 \sqrt{3}) \end{aligned}$ .
::寻找极地坐标(3,-33)。

$\begin{aligned} x = 3 \end{aligned}$ and $\begin{aligned} y = - 3 \sqrt{3} \end{aligned}$
::x=3 和 y33

Draw a right triangle in standard form. Find the distance the point is from the origin and the angle the line segment that represents this distance makes with the +x axis:
::以标准格式绘制右三角形。查找点与源值的距离, 以及代表此距离的线条段与 +x 轴的角 :

$\begin{aligned} r = \sqrt{3^{2} + (- 3 \sqrt{3})^{2}} \end{aligned}$
::r=32+(-33)2

$\begin{aligned} = \sqrt{9 + 27} \end{aligned}$

$\begin{aligned} = \sqrt{36} \end{aligned}$

$\begin{aligned} = 6 \end{aligned}$

And for the angle,
::对于角度,

$\begin{aligned} tan θ_{r e f} = | \frac{(- 3 \sqrt{3})}{3} | \end{aligned}$
:- 333)3

$\begin{aligned} tan θ_{r e f} = \sqrt{3} \end{aligned}$
::棕色 & erref= 3

$\begin{aligned} θ_{r e f} = {tan}^{- 1} \sqrt{3} \end{aligned}$
::ref=tan-13

$\begin{aligned} θ_{r e f} = \frac{π}{3} \end{aligned}$
::瑞夫3号

So, $\begin{aligned} θ_{r e f} = \frac{π}{3} \end{aligned}$ and we can look at the signs of x and y -- (+, -) -- to see that $\begin{aligned} θ = \frac{5 π}{3} \end{aligned}$ since it is a 4 ^th quadrant angle.
::所以,“ref}3”和我们可以看到 x 和 y - (+, -) 的符号, 来看到 \\\ 5\ 3, 因为它是第 4 象限角度。

The rectangular point $\begin{aligned} (3, - 3 \sqrt{3}) \end{aligned}$ is equivalent to the polar point $\begin{aligned} (6, \frac{5 π}{3}) \end{aligned}$ .
::矩形点(3,-3,-3)相当于极点(6,53)。

Recall that when solving for θ , we used
::记得当我们解决的解决时,我们用

$\begin{aligned} tan θ = | \frac{(- 3 \sqrt{3})}{3} | \end{aligned}$ or $\begin{aligned} tan θ = \sqrt{3} \end{aligned}$
::或棕色 3

We found
::我们找到了

$\begin{aligned} θ = \frac{5 π}{3} \end{aligned}$ . BUT, θ could also be $\begin{aligned} θ = \frac{2 π}{3} \end{aligned}$ . You must examine the signs of each coordinate to see that the angle must be in the fourth quadrant in rectangular units or between $\begin{aligned} \frac{3 π}{2} \end{aligned}$ and 2π in polar units. Of the two possible angles for θ, only $\begin{aligned} \frac{5 π}{3} \end{aligned}$ is valid. Note that when you use tan ^-1 on a calculator you will always get an answer in the range $\begin{aligned} - \frac{π}{2} \leq θ \leq \frac{π}{2} \end{aligned}$ .
::533. 但是, 也可以是23。您必须检查每个坐标坐标的标记, 才能看到角必须在矩形单位的第四象方块中或在 32 和 2之间, 在极值单位中。在的两个可能的角中, 只有 53 有效。请注意, 当您在计算器上使用 tan-1 时, 您总是会得到 22 的答案。

Example 4
::例4

Convert the following rectangular coordinates to polar coordinates.
::将以下矩形坐标转换为极坐标。

$\begin{aligned} (3, 3 \sqrt{3}) \end{aligned}$

$\begin{aligned} (6, 66^{\circ}) \end{aligned}$

$\begin{aligned} (- 2, 2) \end{aligned}$

$\begin{aligned} (2 \sqrt{2}, 225^{\circ}) \end{aligned}$

Convert the following polar coordinates to rectangular coordinates.
::将以下极坐标转换为矩形坐标。

$\begin{aligned} (4, \frac{2 π}{3}) \end{aligned}$

$\begin{aligned} (- 2, 2 \sqrt{3}) \end{aligned}$

$\begin{aligned} (- 1, \frac{5 π}{6}) \end{aligned}$

$\begin{aligned} (\frac{\sqrt{3}}{2}, - \frac{1}{2}) \end{aligned}$

Example 5
::例5

Express the equation in rectangular form: $\begin{aligned} r = 6 c o s θ \end{aligned}$ .
::矩形表示方程式:r=6cos。

$\begin{aligned} r^{2} = 6 r c o s θ \end{aligned}$ : multiply both sides by $\begin{aligned} r \end{aligned}$
::r2= 6rcos : 将两边乘以 r

$\begin{aligned} x^{2} + y^{2} = 6 x \end{aligned}$ : Using $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$ and $\begin{aligned} x = r c o s θ \end{aligned}$
::x2+y2=6x : 使用 x2+y2=r2 和 x=rcos

$\begin{aligned} ∴ x^{2} + y^{2} = 6 x \end{aligned}$ is the equation in rectangular form.
::x2+y2=6x是矩形方程式。

Example 6
::例6

Express the equation in rectangular form: $\begin{aligned} r = 6 \end{aligned}$ .
::以矩形形式表示方程式:r=6。

This one is easy:
::这很简单:

$\begin{aligned} r = 6 \end{aligned}$ is the polar form of the equation for a circle
::r=6 是圆形方程式的极形

$\begin{aligned} r^{2} = 6^{2} \end{aligned}$ : square both sides
::r2=62:双方平方

$\begin{aligned} x^{2} + y^{2} = 36 \end{aligned}$ : Using $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$ and simplifying
::x2+y2=36 : 使用 x2+y2=r2 并简化

$\begin{aligned} ∴ x^{2} + y^{2} = 36 \end{aligned}$ is the equation in rectangular form.
::+2+y2=36 是矩形方程式。

Review
::回顾

How is the point with polar coordinates $\begin{aligned} (5, π) \end{aligned}$ represented in rectangular coordinates?
::矩形坐标中以极坐标(5 )表示的点值(5 )如何?

Plot each point below in polar coordinates (r, θ). Then write the rectangular coordinates (x, y) for the point.
::在极坐标(r, )下绘制下方的每个点。然后写出点的矩形坐标( x, y)。

$\begin{aligned} (3, 60^{o}) \end{aligned}$
:3 600o)

$\begin{aligned} (- 10, \frac{π}{3}) \end{aligned}$

$\begin{aligned} (15, π) \end{aligned}$

The rectangular coordinates (x, y) are given. For each question: a) Find two pairs of polar coordinates (r, θ), one with r > 0 and the other with r < 0. b) Express θ in radians, and round to the nearest hundredth.
::给定矩形坐标(x, y)。每个问题a) 找出两对极坐标(r, ),一对极坐标(r, ),一对极坐标(r, ),一对极坐标(r > 0),另一对角坐标(r < 0. b) ,以弧度表示Express ,圆到最接近的一百度。

$\begin{aligned} (5, - 5) \end{aligned}$

$\begin{aligned} (0, 10) \end{aligned}$

$\begin{aligned} (- 8, 6) \end{aligned}$

Transform each polar equation to an equation using rectangular coordinates. Identify the graph, and give a rough sketch or description of the sketch.
::使用矩形坐标将每个极方程转换为方程。标明图形, 并给出粗略的草图或草图描述。

$\begin{aligned} θ = \frac{π}{10} \end{aligned}$

$\begin{aligned} r = 8 \end{aligned}$
::r=8

$\begin{aligned} r s i n θ = 7 \end{aligned}$
::罗辛7

$\begin{aligned} r c o s θ = - 3 \end{aligned}$
::rcos 3

Transform each rectangular equation to an equation using polar coordinates. Identify the graph, and give a rough sketch or description of the sketch.
::使用极坐标将每个矩形方程式转换为方程式。标明图形, 并给出粗略的草图或草图描述。

$\begin{aligned} x^{2} + y^{2} - 2 x = 0 \end{aligned}$
::x2+y2 - 2x=0

$\begin{aligned} y = \sqrt{3} x \end{aligned}$
::y=3x y=3x

$\begin{aligned} y = - 5 \end{aligned}$
::y 5

$\begin{aligned} x y = 15 \end{aligned}$
::xy= 15

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

极地和笛卡尔转变

Polar and Cartesian Transformation ::极地和笛卡尔转变

Polar Form to Rectangular Form ::极表到矩形表

Rectangular Form to Polar Form ::矩形窗体到极形的矩形窗体

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Polar and Cartesian Transformation
::极地和笛卡尔转变

Polar Form to Rectangular Form
::极表到矩形表

Rectangular Form to Polar Form
::矩形窗体到极形的矩形窗体

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)