12.10 树图图和概率分布

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节树图图和概率分布

  折叠 展开

  树图图和概率分布

  播放段落

  In any given day of the week, there is a 62% likelihood that it will be cloudy in Seattle. What is the probability that there will be less than 3 cloudy days in Seattle during your one-week visit?
  ::在每周的某一天里,西雅图有62%的可能性会阴云。 在你为期一周的访问中,西雅图的云天将少于3天的可能性有多大?

  播放段落

  Probability Distribution
  ::概率分布

  播放段落

  Sometimes it is useful to create a tree diagram to illustrate the possible outcomes of multiple events and their individual probabilities, calculate the probabilities of the combined events and the sample space . In other cases, we might use combinations or permutations to create a table. A Probability Distribution is a table which includes all possible outcomes (sample space) and their respective probabilities.
  ::有时,创建一个树形图以说明多个事件及其个别概率的可能结果、计算合并事件概率和样本空间是有益的。在另一些情况下,我们可以使用组合或变相来创建表格。概率分布是一个包括所有可能的结果(抽样空间)及其各自概率的表格。

  播放段落

  Let's solve the following problems.
  ::让我们解决以下的问题。

  播放段落
  1. A game of chance involves flipping a coin and selecting a chip from one of two urns. If the coin toss results in heads, then you select from urn A which contains 8 yellow chips and 5 green chips. If the coin toss results in tails, then you select from urn B which contains 6 yellow chips and 6 green chips. Use this information to create a tree diagram illustrating the possible outcomes and their probabilities and then determine the probability of selecting a yellow chip.
     ::机会游戏涉及翻硬币和从两分之一的骨灰体中选择一个芯片。 如果硬币投向头部, 那么您从包含 8 个黄色芯片和 5 个绿色芯片的 urn A 中选择一个。 如果硬币投向尾巴, 那么从 urn B 中选择一个包含 6 个黄色芯片和 6 个绿色芯片的 urn B 中选择一个。 使用此信息创建树图, 显示可能的结果及其概率, 然后确定选择黄色芯片的概率 。

  播放段落

  First, we need to make a tree diagram. The first branches of the diagram show the coin toss results and the second sets of branches show the chip selection results. Notice that each set of branches in the tree diagram has probabilities which sum to 1. This happens because one of the outcomes must occur. In other words, you either select a yellow or a green chip (there is no other outcome in the sample space) so the sum of the probabilities will be 1. These types of events are called Complimentary Events .
  ::首先,我们需要绘制一个树图。 图表的第一个分支显示硬币投出结果, 第二组分支显示芯片选择结果。 请注意, 树图中的每组树枝的概率等于 1 。 发生这种情况是因为结果之一必须发生。 换句话说, 您要么选择一个黄色芯片, 要么选择一个绿色芯片( 样本空间中没有其他结果) , 因此概率的总和将是 1 。 这些类型事件被称为“ 辅助事件 ” 。

  

  播放段落

  By multiplying “across” the branches, we can determine the probabilities of the combined events. Now, look at the sum of the probabilities on the far right: $\begin{align*}\frac{4}{13}+\frac{5}{26}+\frac{1}{4}+\frac{1}{4}=1\end{align*}$ . The entire sample space is shown here so the sum of the probabilities of all the possible outcomes should be 1. This is an excellent way to check for accuracy in your tree diagram calculations.
  ::将“ 跨” 分支乘以“ 跨” 分支, 我们就可以确定合并事件的概率。 现在, 看看极右的概率总和: 413+526+14+14+14=1。 这里显示的是整个样本空间, 这样所有可能结果的概率总和应该是 1 。 这是检查树图计算准确性的最佳方法 。

  播放段落

  Now, to answer the question: What is the probability of selecting a yellow chip? Looking at the diagram, there are two ways to select a yellow chip. One, we could toss the coin and get heads and then select a yellow chip from urn A and this probability is $\begin{align*}\frac{4}{13}\end{align*}$ . Two, we could toss the coin and get tails and then select a yellow chip and this probability is $\begin{align*}\frac{1}{4}\end{align*}$ . We can add the probabilities of these two “paths” to the same end result and get $\begin{align*}\frac{4}{13}+\frac{1}{4}=\frac{29}{52} \thickapprox 0.5577\end{align*}$ .
  ::现在,回答一个问题:选择黄色芯片的概率是多少?看看图表,有两种选择黄色芯片的方法。第一,我们可以扔硬币,然后得到头部,然后从URn A中选择黄色芯片,这个概率是413。第二,我们可以扔硬币,得到尾巴,然后选择黄色芯片,这个概率是14。我们可以把这两个“路径”的概率加到同一个最终结果上,然后得到413+14=2952\\\0.5577。

  播放段落
  2. In a box of 20 candies, there are 8 which contain nuts. If 5 pieces are randomly selected and consumed, create a probability distribution table to show the probability of selecting 0, 1, 2, 3, 4, or 5 candies which contain nuts in the sample.
     ::在20个糖果盒中,有8个含有坚果。如果随机选择和消费了5个,则创建一个概率分布表,以显示在样本中选择0、1、2、3、4或5个含有坚果的糖果的概率。

  播放段落

  First, let’s create a formula for determining the probability of each of the outcomes. We can use combinations to help us do this. First, how many ways are there to select 5 pieces of candy from a box of 20 pieces? This is a , so $\begin{align*}_{20}C_5\end{align*}$ or $\begin{align*}\dbinom{20}{5}\end{align*}$ . This value will be the total number of possible outcomes and thus the denominator of our probability ratio. Now, how many ways are there to select 0 of the 8 candies with nut and 5 of the 12 candies without nuts? Again, we have combinations and their product can be found for the numerator of our probability ratio: $\begin{align*}\dbinom{8}{0} \dbinom{12}{5}\end{align*}$ . Now we can put it all together and find the probability of selecting 0 candies with nuts: $\begin{align*}\frac{\dbinom{8}{0} \dbinom{12}{5}}{\dbinom{20}{5}}=\frac{33}{646} \thickapprox 0.05108\end{align*}$
  ::首先,让我们创建一个公式来决定每个结果的概率。 我们可以使用组合来帮助我们做到这一点。 首先, 有多少种方法可以从一个20块的盒子中选择5块糖果? 这是一个, 所以 20C5 或 (205 ) 。 这个数值将是可能结果的总数, 也就是我们概率比率的分母 。 现在, 有多少种方法可以选择8个带坚果的糖果中的0个和12个没有坚果的糖果中的5个? 再说一遍, 我们的概率比率计数器可以找到组合和它们的产品 80 (125) 现在, 我们可以把它们组合在一起, 并找到用坚果选择0个糖果的可能性 : (80)( 125) (205) = 33646 0.05108) 。

  播放段落

  Similarly, for 1 candy containing nuts: $\begin{align*}\frac{\dbinom{8}{1} \dbinom{12}{4}}{\dbinom{20}{5}}=\frac{165}{646} \thickapprox 0.25542\end{align*}$
  ::同样,1个含有坚果的糖果81)(124)(205)=1656460.25542)

  播放段落

  For 2 candies with nuts we get: $\begin{align*}\frac{\dbinom{8}{2} \dbinom{12}{3}}{\dbinom{20}{5}}=\frac{385}{969} \thickapprox 0.39732\end{align*}$ , and so on.
  ::对于两个带坚果的糖果,我们得到82)(123)(205)=3859690.39732,等等)。

  播放段落

  The table below  shows all of the final probabilities for each outcome in the sample space. This is called a Probability Distribution Table.
  ::下表显示了样本空间中每项结果的所有最终概率,称为概率分布表。

  播放段落

  What happens if we add up all of the probabilities in this table?
  ::如果我们把这张桌子上所有的概率加在一起会怎么样?

  $\begin{align*}0.05108 + 0.25542 + 0.39732 + 0.23839 + 0.05418 + 0.00361 = 1\end{align*}$

  播放段落

  This means that the probability of getting one of these outcomes is 100%. Also, this shows that our probability distribution is correct because we have included all of the possible outcomes and the sum of their probabilities is 1. In other words, this illustrates that there are no other possible outcomes since there is a 100% chance of getting one of these results.
  ::这意味着获得其中一种结果的概率是100%。 此外,这也表明我们的概率分布是正确的,因为我们已经包括了所有可能的结果,而其概率的总和是1。 换句话说,这表明没有其他可能的结果,因为获得其中一种结果的可能性是100%。

  Number of Candies Selected Containing Nuts	Probability
  0	$\begin{align*}\frac{33}{646} \thickapprox 0.05108\end{align*}$
  1	$\begin{align*}\frac{165}{646} \thickapprox 0.25542\end{align*}$
  2	$\begin{align*}\frac{385}{969} \thickapprox 0.39732\end{align*}$
  3	$\begin{align*}\frac{77}{323} \thickapprox 0.23839\end{align*}$
  4	$\begin{align*}\frac{35}{646} \thickapprox 0.05418\end{align*}$
  5	$\begin{align*}\frac{7}{1938} \thickapprox 0.00361\end{align*}$

  播放段落
  3. Over time, Ronald has shown that in 2 of 5 attempts he makes a bulls eye with a bow and arrow. Create a probability distribution table which shows the possible outcomes and the associated probabilities when Ronald shoots three arrows.
     ::随着时间的推移,罗纳德已经证明,在5次尝试中的2次中,他用弓箭做牛眼。 创建一个概率分布表,显示罗纳德射3支箭时可能的结果和相关概率。

  播放段落

  First, we will consider each bulls eye a success and each non bulls eye a failure. So, the probability of a success is $\begin{align*}\frac{2}{5}\end{align*}$ and the probability of a failure is $\begin{align*}\frac{3}{5}\end{align*}$ . The probability of zero successes is $\begin{align*}\left(\frac{3}{5}\right)^3=\frac{27}{125}=0.216\end{align*}$ . Similarly, the probability of three successes is $\begin{align*}\left(\frac{2}{5}\right)^3=\frac{8}{125}=0.064\end{align*}$ . With three shots, there are two other possibilities to consider. Ronald could also have one success and two failures or two successes and one failure. In these cases, we must consider that any one or two of the shots could be successes so we will multiply by the number of “combinations” that are possible. For example, if Ronald has one success, then there are $\begin{align*}\dbinom{3}{1}\end{align*}$ or 3 ways this could occur: SFF, FSF or FFS. So we will multiple the combinations by the probability of one success and two failures: $\begin{align*}\tbinom{3}{1} \left(\frac{2}{5}\right)^1 \left(\frac{3}{5}\right)^2=\frac{54}{125}=0.432\end{align*}$ . For two successes and one failure we have $\begin{align*}\tbinom{3}{2} \left(\frac{2}{5}\right)^2 \left(\frac{3}{5}\right)^1=\frac{36}{125}=0.288\end{align*}$ . Now, make a probability distribution table:
  ::首先,我们将认为每只公牛的眼睛都是成功的,每一只非公牛的眼睛都是失败的。因此,成功概率为25,失败概率为35。零成功概率为(353=27125=0.216. ) 零成功概率为(353=27125=0.216. 类似地,三次成功概率为(253=8125=0.064 ) 。同样,有另外两种可能性可以考虑。罗纳德也可以有一个成功和两个失败或两个成功或一个失败。在这些案例中,我们必须考虑其中任何一个或两个失败都可能是成功,这样我们就能够乘以可能的“组合”数量。例如,如果罗纳德有一个成功,那么就会有(31)或3种可能发生成功或失败的方法:SFF、FSFF或FFS。因此,我们将乘以一个成功和两个失败的几率(31)(251)(352)1(352=54125)=0.432.32。对于两个成功和一个失败,我们必须考虑一个成功和一个失败(32)(252)(351)=36125=0.288)。 现在,请按一个概率分布表:

  Number of Bulls Eyes	Probability
  0	0.216
  1	0.432
  2	0.288
  3	0.064

  播放段落

  This is an example of a special type of probability called a Binomial Probability because its rule resembles the Binomial Theorem. In order for a problem to be a binomial probability it must consist of multiple independent trials, called Bernoulli Trials, in which there is either a success or a failure. In other words, $\begin{align*}P(\text{success}) + P(\text{failure}) = 1\end{align*}$ and the result of each trial is independent of the result of a previous trial.
  ::这是一个特殊概率类型的例子,被称为二元概率,因为其规则类似于二元论。 如果问题要成为二元概率,它必须包括多个独立的审判,称为伯诺利审判,其中要么成功,要么失败。换句话说,P(成功)+P(失败)=1,每次审判的结果独立于先前审判的结果。

  播放段落

  If we let $\begin{align*}n = \text{number of trials}\end{align*}$ , $\begin{align*}p = \text{probability of a success}\end{align*}$ and $\begin{align*}r = \text{number of successes}\end{align*}$ , we can use the following formula to determine the probability of any number of successes.
  ::如果我们使用n=试验次数、p=成功概率和r=成功次数,我们可以使用以下公式来确定成功次数的概率。

  播放段落

  $$\begin{align*}P( r \ \text{successes}) = \dbinom{n}{r}(p)^r(1-p)^{n-r}.\end{align*}$$
  ::P(r 成功)=(nr (p)r(1-p)n-r。

  播放段落

  Notice that this formula is exactly what we did to find the probability of Ronald shooting two bulls eyes:
  ::注意这个公式正是我们所做的 来发现Ronald射杀两只公牛眼睛的概率:

  播放段落

  For two bulls eyes, $\begin{align*}n=3\end{align*}$ , $\begin{align*}p=\frac{2}{5}\end{align*}$ , and $\begin{align*}r=2\end{align*}$ : $\begin{align*}\dbinom{3}{2} \left(\frac{2}{5}\right)^2 \left(1- \frac{2}{5}\right)^{3-2}=\dbinom{3}{2} \left(\frac{2}{5}\right)^2 \left(\frac{3}{5}\right)^1=\frac{36}{125}=0.288\end{align*}$ .
  ::对于两只公牛的眼睛, n=3, p=25, r=232)(25)(2)(1-25)3-2=(32)(25)(2)(35)1=36125=0.288)。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find  the probability that there will be less than 3 cloudy days in Seattle during your one-week visit. 
  ::早些时候,你被要求去西雅图找寻 在你为期一周的访问中 可能不到3天的云天

  播放段落

  Less than seven cloudy days implies that there could be 0, 1, or 2 cloudy days during your one-week visit. We can add these individual probabilities to determine the probability. For the Binomial Probability, $\begin{align*}n=7\end{align*}$ (since there are 7 days in a week), $\begin{align*}p=0.62\end{align*}$ and $\begin{align*}r\end{align*}$ takes on the values 0, 1 and 2.
  ::少于七天的云天意味着在您一周的访问中可能有0天、1天或2天的云天。 我们可以添加这些个别概率来确定概率。 对于二元概率, n=7 (因为每周有7天), p=0.62 和 r 以 0, 1 和 2 值为准。

  $$\begin{align*}\dbinom{7}{0}(0.62)^0(0.38)^7+\dbinom{7}{1}(0.62)^1(0.38)^6+ \dbinom{7}{2}(0.62)^2(0.38)^5=0.0.001144 + 0.01306774 + 0.06396902568 = 0.07818076568\end{align*}$$

  播放段落

  Therefore, there is only about a 7.8% chance that less than 3 days of your trip will be cloudy. Better make sure to pack an umbrella!
  ::因此,只有7.8%的可能性,不到3天的行程会阴云。 最好记得打包伞!

  播放段落

  Example 2
  ::例2

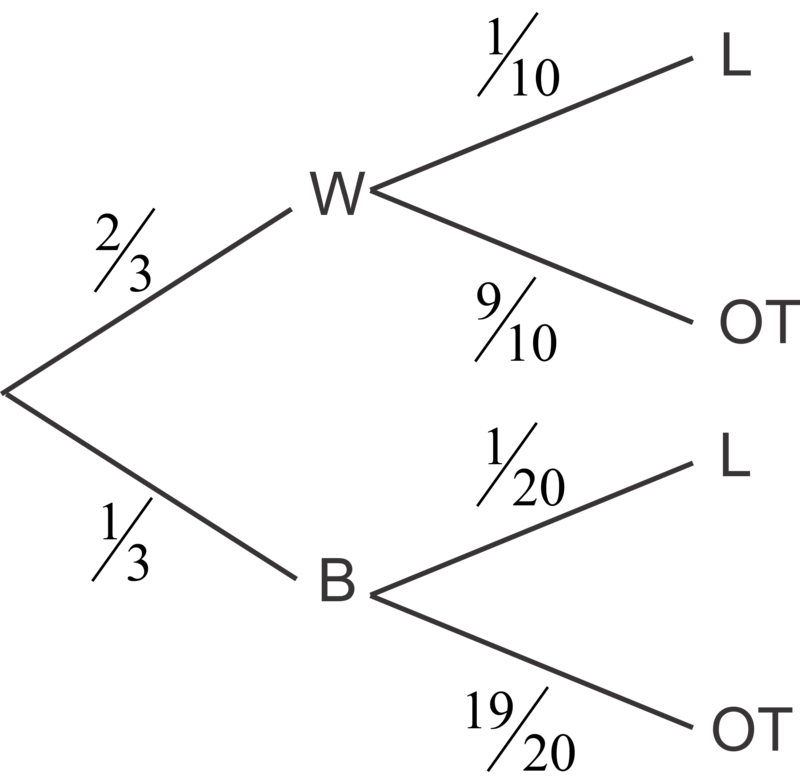
  播放段落

  Sarah either walks or rides the bus to school. When she walks she is more likely to be late to school than when she rides the bus. Complete the tree diagram and find the probability that Sarah is late for school.
  ::Sarah要么走路,要么乘公交车上学。当她走路时,她比乘公交车时更有可能迟到。完成树图,发现Sarah上学时可能迟到。

  

   

  播放段落

  To find the probability that Sarah is late we need to add the probabilities of the two different ways she can be late. She can walk and be late or she can ride the bus and be late:
  ::为了发现莎拉迟到的概率,我们需要加上她可能迟到的两种不同方式的概率。她可以走路和迟到,或者坐公共汽车和迟到:

  播放段落

  $\begin{align*}P(\text{walk and late}) + P(\text{bus and late}) =\left(\frac{2}{3}\right) \left(\frac{1}{10}\right)+ \left(\frac{1}{3}\right) \left(\frac{1}{20}\right)=\frac{1}{12} \thickapprox 0.08333\end{align*}$
  ::P(行走和迟到)+P(客车和迟到)=(23)(110)+(13)(120)=1120.08333

  播放段落

  Example 3
  ::例3

  播放段落

  In a case of 15 light bulbs there are 2 defective bulbs. Create a probability distribution which illustrates the possible outcomes and their respective probabilities if we randomly select 3 bulbs from the box. Show that the sum of the probabilities is 1.
  ::在15个灯泡中,有2个有缺陷的灯泡。如果我们随机从盒子中选择3个灯泡,则建立概率分布,显示可能的结果和各自的概率。显示概率之和是1。

  Number of defective bulbs	Probability
  0	$\begin{align*}\frac{\dbinom{2}{0} \dbinom{13}{3}}{\dbinom{15}{3}}=0.628571\end{align*}$
  1	$\begin{align*}\frac{\dbinom{2}{1} \dbinom{13}{2}}{\dbinom{15}{3}}=0.342857\end{align*}$
  2	$\begin{align*}\frac{\dbinom{2}{2} \dbinom{13}{1}}{\dbinom{15}{3}}=0.028571\end{align*}$

  $\begin{align*}0.62857 + 0.342857 + 0.028571 = 0.999998\end{align*}$

  播放段落

  Since we rounded the individual probabilities, the sum may reflect this inaccuracy. For all intents and purposes, this answer is 1.
  ::由于我们四舍五入了个别概率,这一数额可能反映了这一不准确性。

  播放段落

  Note that it is not possible to select a sample containing 3 defective bulbs because there are only 2 defective bulbs in the box.
  ::请注意,无法选择含有3个有缺陷的灯泡的样本,因为盒子里只有2个有缺陷的灯泡。

  播放段落

  Example 4
  ::例4

  播放段落

  On any given workday, there is a 15% chance that Professor Calculus will cause an explosion in his laboratory. Use the Binomial Probability formula to determine the probability that Professor Calculus will cause less than three explosions in a five day work week.
  ::在任何工作日,卡尔库卢斯教授有15%的几率在其实验室引起爆炸。 使用二元概率公式来确定卡尔库卢斯教授在五天工作周内造成不到三次爆炸的几率。

  播放段落

  Less than three explosions implies that Professor Calculus could cause 0, 1 or 2 explosions in the work week. We can add these individual probabilities to determine the probability. For the Binomial Probability, $\begin{align*}n=5\end{align*}$ (since there are 5 days in the work week), $\begin{align*}p=0.15\end{align*}$ and $\begin{align*}r\end{align*}$ takes on the values 0, 1 and 2.
  ::少于三次爆炸意味着微积分教授可以在工作周内造成0、1或2次爆炸。我们可以添加这些个别概率来确定概率。对于二元概率,n=5(因为工作周有5天),p=0.15和r取用值0、1和2。

  $$\begin{align*}\dbinom{5}{0}(0.15)^0(0.85)^5+\dbinom{5}{1}(0.15)^1(0.85)^4+ \dbinom{5}{2}(0.15)^2(0.85)^3=0.443705 + 0.391505 + 0.138178 = 0.973388\end{align*}$$

  播放段落

  Review
  ::回顾

  播放段落

  Jamie and Olivia are best friends and neighbors. As such they often eat dinner together at one of their houses. About 30% of the time, they eat at Jamie’s house and her mother makes a non vegetarian meal 65% of the time. The rest of the time, they eat at Olivia’s house and her mother serves a vegetarian meal 55% of the time.
  ::杰米和奥利维亚是最好的朋友和邻居。 因此,他们经常在他们家中一起吃晚饭。 大约30%的时间,他们在杰米家吃饭,而她母亲做非素食餐的时间占65%。 剩下的时间,他们在奥利维亚家吃饭,而她母亲做素食餐的时间占55%。

  播放段落
  1. Make a tree diagram, including the appropriate probabilities to illustrate this scenario.
     ::绘制一棵树图,包括说明这一情景的适当概率。
  播放段落
  2. What is the probability of going to Olivia’s house and eating a meal containing meat?
     ::前往Olivia家吃一顿含有肉的饭的几率有多大?
  播放段落
  3. What is the probability that the girls will eat a vegetarian dinner?
     ::女孩们吃素食晚餐的几率有多大?

  播放段落

  Tommy has 20 water balloons in bucket. There is a $\begin{align*}\frac{1}{8}\end{align*}$ chance of each balloon exploding on him before he even has a chance to throw it. Use a Binomial Probability Distribution to answer the following questions.
  ::汤米在桶里有20个水气球。 每只气球有18次爆炸的机率在他甚至有机会扔之前就爆炸。 使用一个二元概率分布来回答下列问题 。

  播放段落
  4. What is the probability that Tommy throws eight without any breaking on him?
     ::汤米投出八分的概率是多少?
  播放段落
  5. What is the probability that exactly five of the eight balloons he attempts to throw explode on him?
     ::在他试图向他投掷的八个气球中,确切的五个气球爆炸的可能性有多大?
  播放段落
  6. What is the probability that more than two of the eight explode on him?
     ::八人中有二人以上的爆炸机率有多大?

  播放段落

  A vaccine has a 92% success rate. The vaccine is given to 50 patients in a medical practice. Use a Binomial Probability Distribution to answer the following questions.
  ::疫苗的成功率为92%,在医疗实践中,50名病人接种了疫苗,使用二元概率分布来回答下列问题。

  播放段落
  7. What is the probability that it works for all patients?
     ::它对所有病人有效的可能性有多大?
  播放段落
  8. What is the probability that is fails for exactly 9 patients?
     ::9个病人的失败概率是多少?
  播放段落
  9. What is the probability that it fails for more than 1 patient?
     ::超过1个病人的失败概率是多少?

  播放段落

  Five cards are randomly selected from a deck of cards.
  ::五张卡片是从牌牌牌牌中随机选取的。

  播放段落
  10. Create a probability distribution table for the number of “high” cards (jack, queen, king or ace) in a 5 card hand chosen at random.
      ::为随机选择的5张卡手中的“高”卡片数(杰克、皇后、王牌或王牌)创建一个概率分布表。
  播放段落
  11. What is the probability of getting at least one high card?
      ::获得至少一张高卡的可能性有多大?
  播放段落
  12. What is the probability of getting at least two?
      ::获得至少两个的可能性有多大?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。