13.1 毕达哥里安神论及其交汇
Section outline
-
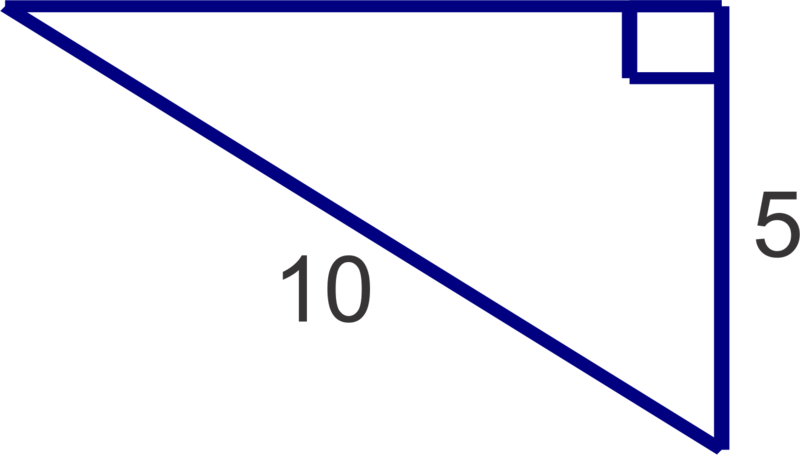
Mr. Aubel wants to rope off half of his rectangular garden plot to keep the deer out. He will run the rope around the outside of the garden and diagonally down the center to form a right triangle . The garden measures 5 yards by 8 yards. How many full yards of rope does Mr. Aubel need?
::Aubel先生想把一半的长方形花园的地块绳子绑起来,把鹿拖出来。他将绕着花园外面的地盘跑绳子,然后从中间直奔中间,形成一个右三角形。花园的5码乘8码乘8码。Aubel先生需要多少长的绳子?Pythagorean Theorem and Its Converse
::毕达哥里安神论及其交汇The Pythagorean Theorem refers to the relationship between the lengths of the three sides in a right triangle. It states that if and are the legs of the right triangle and is the hypotenuse , then . For example, the lengths 3, 4, and 5 are the sides of a right triangle because . Keep in mind that is always the longest side.
::Pytagorean Theorem 指的是右三角形中三边长度之间的关系。 它指出, 如果 a和 b 是右三角形的腿, c 是下限, 那么 a2+b2=c2. 例如, 3、 4和 5 是右三角形的两边, 因为 32+42=52( 9+16=25) 。 记住 c 总是最长的一面 。The converse of this statement is also true. If, in a triangle , is the length of the longest side and the shorter sides have lengths and , and , then the triangle is a right triangle.
::此语句的反义也是正确的。 如果在三角形中, c 是最长的边的长度, 较短的边有 a 和 b 的长度, 和 a2+b2=c2 的长度, 那么三角形是一个右三角形 。Proof of Pythagorean Theorem
::毕达哥里安神论的证明There are many and here is one of them. We will be using the concept that the area of a figure is equal to the sum of the areas of the smaller figures contained within it and algebra to derive the Pythagorean Theorem.
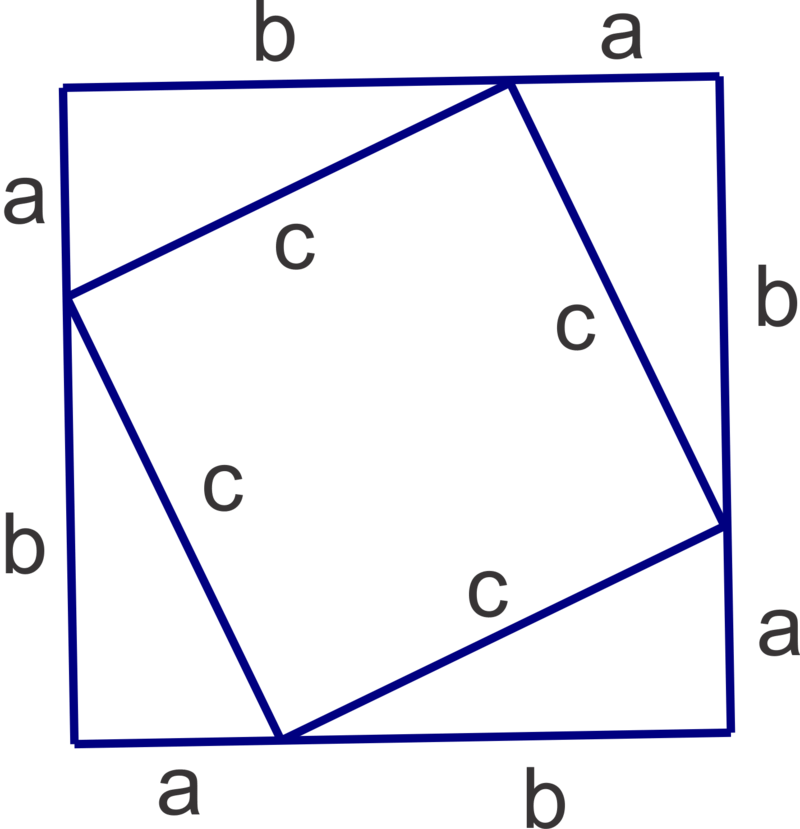
::有很多这样的数字。 我们将使用这个概念, 一个数字的面积等于它所含较小数字的面积和代数的总和, 来产生比达哥伦神话。Using the figure below (a square with a smaller square inside), first write two equations for its area, one using the lengths of the sides of the outer square and one using the sum of the areas of the smaller square and the four triangles.
::使用下图(一个内方较小方的广场),首先为其区域写两个方程式,一个方程式使用外方形两侧的长度,一个方程式使用较小方形和四个三角形的面积之和。Area 1:
::面积1a+b)2=a2+2ab+b2
Area 2:
::面积2:c2+4(12ab)=c2+2abNow, equate the two areas and simplify:
::现在,将这两个领域等同起来,并简化:
::a2+2ab+b2=c2+2aba2+b2=c2Finding a missing side
::寻找缺失的一面In a right triangle and , let's find the length of the third side.
::在右三角形a=7和c=25中,让我们找到第三边的长度。We can start by substituting what we know into the Pythagorean Theorem and then solve for the unknown side, :
::我们可以先把我们所知道的东西 换成毕达哥里安神话 然后解决未知的一面 b:
::72+b2=2524=24=72+b2=2524+b2=625b2=576b=24Now, let's find the length of the third side of the triangle below and leave our answer in reduced radical form.
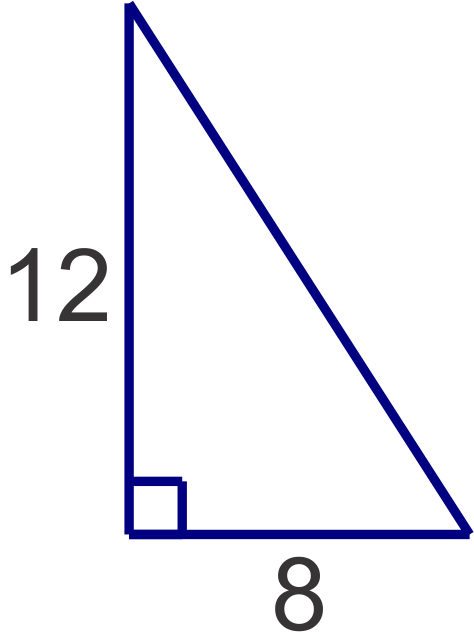
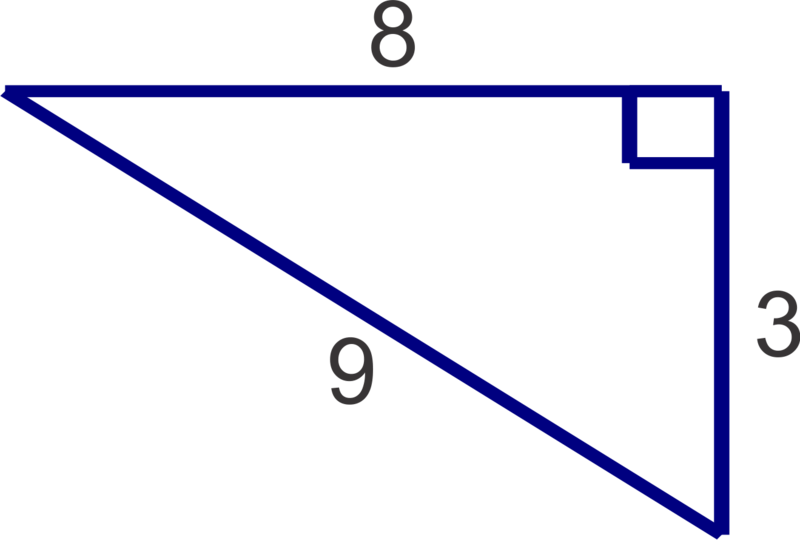
::现在,让我们找到下面三角形第三边的长度 并让我们的答案 降低激进的形式。Since we are given the lengths of the two legs, we can plug them into the Pythagorean Theorem and find the length of the hypotenuse.
::既然我们得到了两条腿的长度 我们可以把它们塞进毕达哥里安神话中 并找到下限的长度
::82+122=c264=c144=c2c2=c2c2=208c=208=208=16/13=413Finally, let's determine whether a triangle with lengths 21, 28, 35 is a right triangle.
::最后,让我们来决定一个长度为21,28,35的三角形是否右三角形。We need to see if these values will satisfy . If they do, then a right triangle is formed. So,
::我们需要看看这些值是否满足 a2+b2=c2. 如果满足,则形成一个右三角形。所以,Yes, the Pythagorean Theorem is satisfied by these lengths and a right triangle is formed by the lengths 21, 28 and 35.
::是的,毕达哥里安神话对这些长度感到满意,右三角形由21、28和35长度组成。Examples
::实例Example 1
::例1Earlier, you were asked to find how many yards of rope Mr. Aubel needs.
::早些时候,你被要求找到 Aubel先生需要多少码绳子We are looking for the perimeter of the triangle. We are given the lengths of the sides so we need to find the hypotenuse.
::我们正在寻找三角形的周边。我们得到了侧面的长度, 所以我们需要找到下限。Let's use the Pythagorean Theorem.
::让我们使用毕达哥伦神话
::52+82=c225+64=c289=c2c=89Now to find the perimeter of the triangle, add the lengths of the three sides.
::现在找到三角形的周边, 加上三边的长度 。Therefore, Mr. Aubel will need 23 yards of rope.
::因此,Aubel先生需要23码的绳子For the given two sides, determine the length of the third side if the triangle is a right triangle.
::对于给定的两边, 如果三角形是右三角形, 请确定第三边的长度 。Example 2
::例2and
::a=10和b=5Example 3
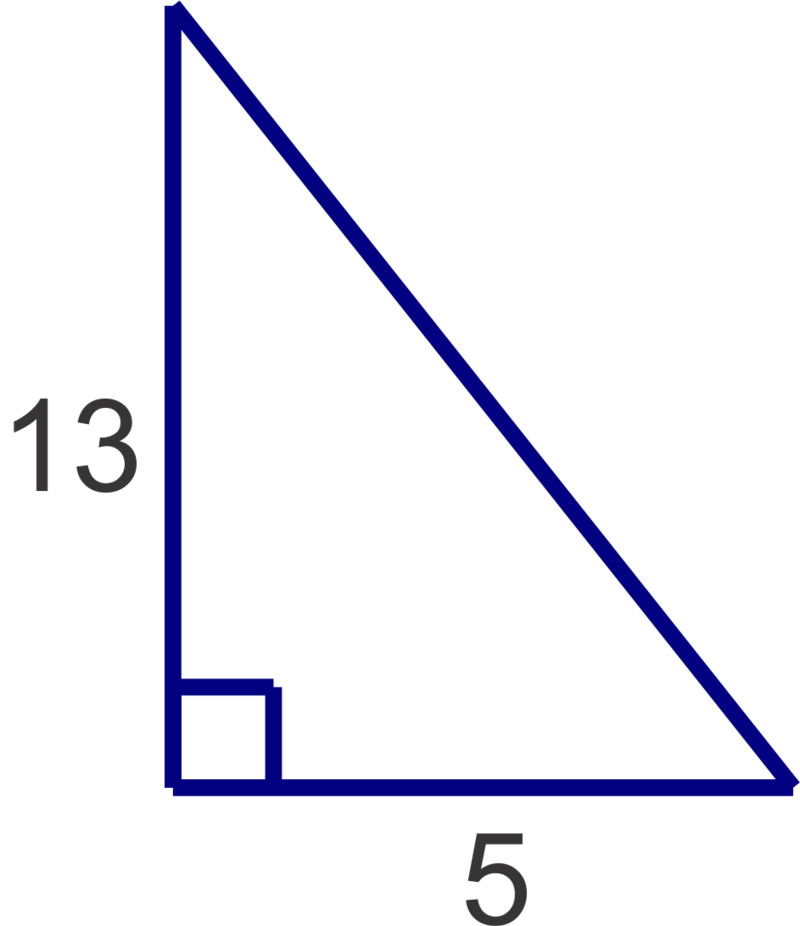
::例3and
::a=5和c=13Use the Pythagorean Theorem to determine if a right triangle is formed by the given lengths.
::使用 Pytagorean 定理符来确定右三角形是否由给定长度组成 。Example 4
::例416, 30, 34
Yes, this is a right triangle.
::162+302=256+900=1156342=1156Example 5
::例59, 40, 42
No, this is not a right triangle.
::92+402=81+1600=1681422=1764 不,这不是右三角形。Example 6
::例62, 2, 4
This one is tricky, in a triangle the lengths of any two sides must have a sum greater than the length of the third side. These lengths do not meet that requirement so not only do they not form a right triangle, they do not make a triangle at all.
::这个问题很棘手, 在三角形中, 任何两边的长度必须有一个大于第三边长度的数值。 这些长度不符合这一要求, 因此不仅不能形成正确的三角形, 根本无法形成三角形 。Review
::回顾Find the unknown side length for each right triangle below.
::查找下面每个右三角形的未知侧边长度。-
-
-
-
::a=6,b=8 -
::b=6,c=14,b=6,c=14 -
::a=12,c=18
Determine whether the following triangles are right triangles.
::确定以下三角是否为右三角。Do the lengths below form a right triangle? Remember to make sure that they form a triangle.
::下方的长度是否形成右三角形 ? 记住要确定它们组成三角形 。- 3, 4, 5
- 6, 6, 11
- 11, 13, 17
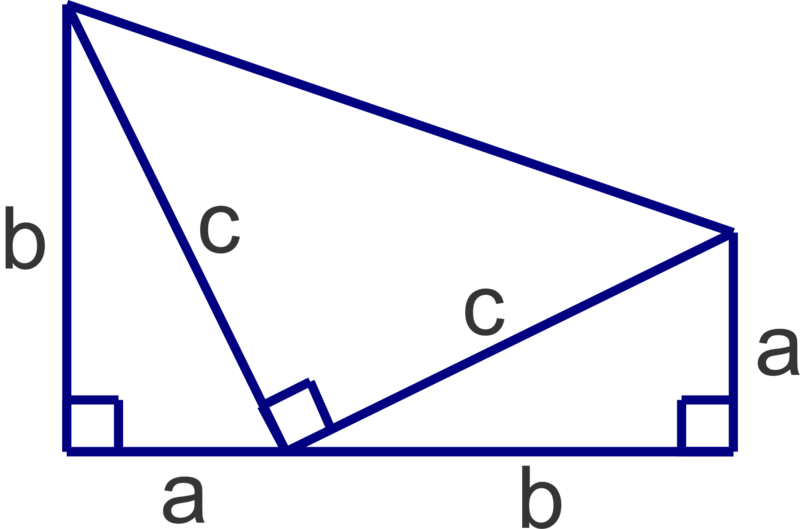
Major General James A. Garfield (and former President of the U.S.) is credited with deriving this proof of the Pythagorean Theorem using a trapezoid. Follow the steps to recreate his proof.
::James A. Garfield少将(美国前总统)利用一个隐形体来推断出毕达哥伦神话的这个证据。-
Find the area of the trapezoid using the trapezoid area formula:
::使用 cugarezoid 区域公式 查找区域区域 : A= 12 (b1+b2) h -
Find the sum of the areas of the three right triangles in the diagram.
::查找图表中三个右三角形区域的总和。 -
The areas found in the previous two problems should be the same value. Set the expressions equal to each other and simplify to get the Pythagorean Theorem.
::前两个问题中发现的区域应该相同值。 设置对等的表达式, 并简化以获取 Pytagoren Theorem 。
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -