5.3 三个不同职位

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三级职位

  Collapse Expand

  三级职位

  播放段落

  Brian just entered the museum. Looking at the "You are here" map, he sees that his favorite exhibit, "Dinosaurs in Motion!" has been moved to the third floor, and is in the fourth room on the right.
  ::布莱恩刚进入博物馆。看看“你在这里”地图, 他看到他最喜欢的展览,“恐龙在运动中!” 已经搬到三楼, 在右边的第四间房。

  播放段落

  Brian knows the museum well, so he knows the entrance is the first room on the left on the first floor, and is already familiar with the museum layout of 8 rooms on each side of the main hall on each floor, with the stairs at the front of the building.
  ::Brian对博物馆很熟悉, 所以他知道入口是一楼左侧的第一个房间, 并且已经熟悉博物馆的布局,

  播放段落

  How could the location of the dinosaur exhibit be described in 3-dimensional coordinates? What is the displacement of the dinosaur room from his position at the front entrance?
  ::如何用三维坐标来描述恐龙展览的位置? 恐龙室从他位于前门入口的位置上移走的原因是什么?

  播放段落

  Three-Dimensional Positions
  ::三级职位

  播放段落

  The rectangular (or Cartesian) coordinate system is used to describe a plane divided into four quadrants , as shown below left. (Note, the colored squares are used to help you visualize the space, remember that the coordinate planes actually extend outward toward infinity.)
  ::矩形(或Cartesian)坐标系统用于描述以下左侧显示的分为四夸的平面。 (注意,彩色方形用于帮助您视觉空间, 记住坐标平面实际上向无穷向外延伸 。 )

  

  播放段落

  The Cartesian coordinate system use to describe three-dimensional space consists of an origin and six open axes, + z and – z are perpendicular to the x-y plane. These axes define three planes which divide the space into eight parts knowns as octants as shown above right. Think of these planes as cutting space three ways: left to right, top to bottom, and front to back.
  ::笛卡尔坐标系统用于描述三维空间,该空间由原体和六个开放轴、+z和-z组成,与X-y平面垂直。这些轴定义了三平面,将空间分为八个部分,如上方所示,八个部分为八位。 将这些飞机视为切除空间的三种方式:左到右,上到下,前到后。

  播放段落

  By convention, we number the four quadrants of the x-y plane in this way: points in quadrant 1 have +x and +y coordinates, those in quadrant 2 have –x and +y, those in quadrant 3 have –x and –y, and those in quadrant 4 have +x and –y. There is currently no standardized numbering system for the octants in three-dimensional space, although most people identify the region with +x, +y, and +z as the first octant. The method used to identify the octants is to indicate verbally the portion of space they occupy. For example, the first octant could also be identified as (top, front, right).
  ::按惯例,我们用这种方式对X-y平面的四四位数进行编号:象限1的点有+x和+y座标,象项2的点有x和+y,象项3的点有x和-y,象项4的点有+x和-y,而象项4的点有+x和-y。目前三维空间的八进制没有标准化的编号系统,尽管大多数人将区域以+x、+y和+z确定为第一个八进制。 用来识别八进体的方法是用口头表示它们占据的空间部分。 比如,第一个八进制也可以被确定为(顶部、前、右 ) 。

  

  播放段落

  Position vectors in 3D space are still represented by arrows that begin at the origin and end at the point in question. The diagram above shows a point, P, located in the front, lower, right octant. The three components of the position vector (P _x , P _y , and P _z ) are shown in the diagram. According to the Pythagorean Theorem, the magnitude of the position vector is given by:
  ::3D 空格中的定位矢量仍然由箭头代表,箭头从源头开始,到有关点结束。上面的图表显示一个点,P,位于前方,下方,右八进制。在图表中显示位置矢量的三个组成部分(Px、Py和Pz)。根据 Pythagoren 理论,位置矢量的大小由下列因素提供:

  播放段落

  $\begin{array}{r}|\stackrel{\to }{P}|=\sqrt{P_x^2+P_y^2+P_z^2}\end{array}$
  ::PPx2+Py2+Pz2

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked a question about Brian, who wants to describe the location of the dinosaur exhibit in 3-dimensions.
  ::早些时候,有人问到关于Brian的一个问题, 他想描述恐龙展览在三层楼的位置。

  播放段落

  Brian knows the museum well, so he knows the entrance is the first room on the left on the first floor, and is already familiar with the museum layout of 8 rooms on each side of the main hall on each floor, with the stairs at the front of the building. How could the location of the dinosaur exhibit be described in 3-dimensional coordinates? What is the displacement of the dinosaur room from his position at the front entrance?
  ::Brian对博物馆很熟悉,因此他知道入口是一楼左侧的第一个房间,并且已经熟悉博物馆在每层大厅两侧8个房间的布局,以及大楼前面的楼梯。 如何用三维坐标描述恐龙展览的位置? 恐龙展览从他位于前门的位子上移到什么位置?

  播放段落

  A coordinate system can be assumed to use any units you wish, in this case the location information is given in units of "rooms" and "floors". Let the x axis represent the horizontal left and right-hand sides of the main halls, y can be the vertical axis, and z can be the front-back axis of rooms down each hall.
  ::可以假设一个坐标系统可以使用您想要的任何单位, 在这种情况下, 位置信息是以“ 房间” 和“ 地板” 的单位提供的 。 让 x 轴代表主大厅的横向左侧和右侧, y 可以是垂直轴, z 可以是每个大厅下的房间的前后方轴 。

  播放段落

  Let Brian's starting position at the entrance represent $\begin{array}{r}(0,0,0)\end{array}$ in three dimensional rectangular coordinates. "Dinosaurs in Motion!" is on the third floor, and is in the fourth room on the right.
  ::让Brian在入口处的开始位置 代表(0,0,0) 在三维的矩形坐标上。“恐龙在运动!”在三楼,在右边的第四间房。

  播放段落

  $\begin{array}{r}(2,3,4)\end{array}$  would represent the dinosaur exhibit room.
  :2,3,4)将代表恐龙展览室。

  播放段落

  Since we were clever, and oriented our coordinate system on the entrance, the vector displacement is the same as the room's location: $\begin{array}{r}⟨2rooms,3floors,4rooms⟩\end{array}$ .
  ::由于我们很聪明,把坐标系统定位在入口处, 矢量移位与房间位置相同: 2房间,3层,4间房。

  播放段落

  Example 2
  ::例2

  播放段落

  Darnell was driving home from a football game in a nearby town when he swerved to avoid a deer which had run onto the road. Fortunately for Darnell, he was able to avoid hitting the deer. Unfortunately, his car ended up in the ditch beside the road. When he was unable to remove the car from the ditch by himself, he walked across a nearby field to the Tucker family farm to ask for help. Darnell later looked at a topographical map and identified his trip across the field. He traveled 300 yards south and 750 yards west from where he left his car. The map showed that he also walked uphill from an altitude of 800 feet to an altitude of 850 feet above sea level. If we treat the location of Darnell’s car as the origin of coordinates, what the position vector of the Tucker farm?
  ::Darnell在附近一个城镇的橄榄球赛场上开车回家,当时他转身躲开一只鹿跑上路。幸运的是,Darnell幸运的是,他能够避免撞到鹿。不幸的是,他的车停在路旁的沟里。当他无法将车从沟里搬走时,他穿过附近的田野,到塔克家农场寻求帮助。Darnell后来看了一张地形图,并确定了他的田间之行。他南行300码,西行750码,离开他的车。地图显示,他也从800英尺的高度上山,到海拔850英尺的高度。如果我们把Darnell家汽车的位置当作坐标来源,塔克农场的位置是什么?

  播放段落

  Define a coordinate system where x = E, y = N, and z = up. Since Darnell walked south and west from the car, the x and y coordinates of the farm are both negative. If we measure all of the distances in feet (1 yard = 3 feet), the farm’s position vector can be written as $\begin{array}{r}\stackrel{\to }{P}=⟨P_{east},P_{north},P_{up}⟩=⟨-2250,-900,50⟩\end{array}$ .
  ::定义坐标系统 x = E, y = N 和 z = 上方的坐标系统。 由于 Darnell 从汽车向南和西行走, 农场的 x 和 y 坐标都是负的。 如果我们测量足足的所有距离(1 码 = 3 英尺) , 农场的位置矢量可以写成 PPast, Pnort, Pnorth, Pup2250, - 9000, 50 。

  播放段落

  Note in this example that Darnell’s walking distance was given in yards, while the elevation change was given in feet. You need to watch out for these small changes when you are solving real-life problems.
  ::请注意,在这个例子中,Darnell的行走距离是用院子给定的,而高度变化则是用脚给定的。 当您正在解决现实生活问题时,您需要注意这些小的改变。

  播放段落

  Example 3
  ::例3

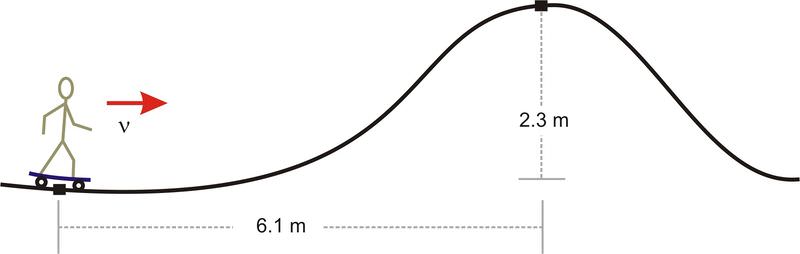
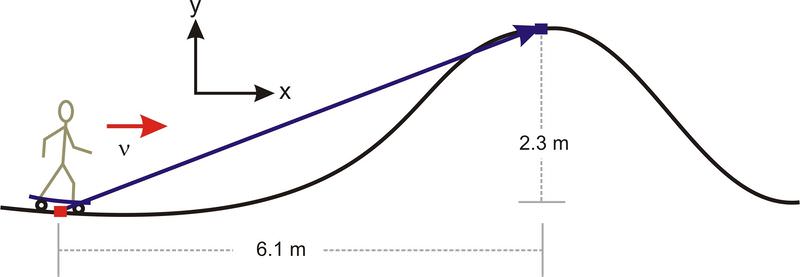
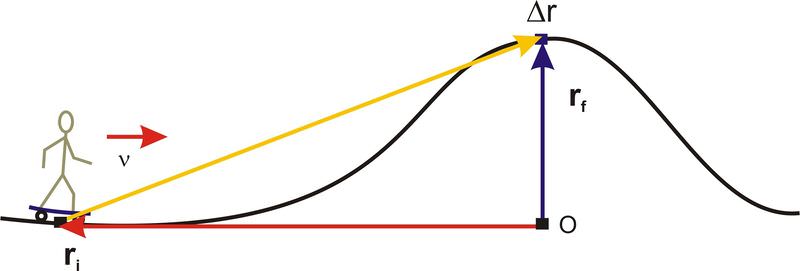
  播放段落

  Zeke is enjoying an afternoon at the local skate-park. The diagram below shows his starting position and his ending position at the highest point on the new hill.
  ::Zeke正在当地滑冰场享受一个下午,下图显示他的起点和在新山顶的最高点的终点。

  播放段落

  Choose two different coordinate systems which could describe this system. Find Zeke’s initial and final position vectors in each of the two coordinate systems. Then identify the displacement vector from his starting position to his final position at the top of the hill.
  ::选择两个不同的坐标系统来描述这个系统 。 在两个坐标系统中的每一个系统中找到 Zeke 的初始位置和最终位置矢量 。 然后从开始的位置到山顶的最后位置来识别移位矢量 。

  

  播放段落

  One possible origin of coordinates is located at Zeke’s starting position. In this case, the initial position vector is given by $\begin{array}{r}\stackrel{\to }{r_i}=⟨0m,0m,0m⟩\end{array}$ and his final position is given by $\begin{array}{r}\stackrel{\to }{r_f}=⟨6.1m,2.3m,0m⟩\end{array}$ . Zeke’s displacement is the difference between these two vectors, $\begin{array}{r}\stackrel{\to }{\mathrm{△}r}=\stackrel{\to }{r_f}-\stackrel{\to }{r_i}=⟨6.1m,2.3m,0m⟩-⟨0m,0m,0m⟩=⟨6.1m,2.3m,0m⟩\end{array}$
  ::坐标来源之一可能位于 Zeke 的起始位置。 在这种情况下, 初始位置矢量由 ri@m, 0m, 0m提供, 其最终位置由 rf\\ 610m, 230m, 0m提供。 Zeke 的偏移是这两个矢量的区别, rärfri610m, 230m, 0m0m, 0m6m, 0m6m, 230m, 0m

  

  播放段落

  Another possible origin of coordinates is at the point marked O in the diagram below. In this case his original position is given by $\begin{array}{r}\stackrel{\to }{r_i}=⟨-6.1m,0m,0m⟩\end{array}$ and his final position is given by $\begin{array}{r}\stackrel{\to }{r_f}=⟨0m,2.3m,0m⟩\end{array}$ . Zeke’s displacement is the difference between these two vectors, $\begin{array}{r}\stackrel{\to }{\mathrm{△}r}=\stackrel{\to }{r_f}-\stackrel{\to }{r_i}=⟨0m,2.3m,0m⟩-⟨-6.1m,0m,0m⟩=⟨6.1m,2.3m,0m⟩\end{array}$
  ::另一个可能的坐标来源是下图中标注的O点。 在这种情况下,他原来的位置由 ri610m,0m,0m提供,他的最后位置由 rf0m,2.3m,0m提供。 Zeke 的偏移是这两个矢量的区别,即 rrffri0m,2.3m,0m610m,0m,0m6m,1m,2.3m,0m1m。

  

  播放段落

  Note that the position vectors representing this motion depend on the choice of coordinate system, but the displacement vector is independent of the coordinate system.
  ::请注意,代表该运动的位置矢量取决于协调系统的选择,但移位矢量独立于协调系统。

  播放段落

  Example 4
  ::例4

  播放段落

  An architecture student designs a spiral staircase, a model of which is shown below. The staircase winds its way around a cylinder of radius 3.5 m and height 11 m. The staircase makes 1 7/8 turns progressing counter-clockwise from its beginning at point A to its end point at B. Using an origin of coordinates at the bottom center of the staircase, determine the position vectors of points A and B. Then find the displacement vector between the two points.
  ::建筑师学生设计螺旋楼梯,其模型如下所示。楼梯在半径3.5米和高度11米的圆柱形周围向风。 楼梯使1/7/8旋转, 从A点开始到B点的终点,逆时针旋转。 使用楼梯下角坐标来源,确定A点和B点的位置矢量。 然后在两点之间找到移位矢量。

  

  播放段落

  As you can see in the top view of the diagram, point A is directly to the left of the origin, therefore the position vector for point A is given by $\begin{array}{r}\stackrel{\to }{r_A}=⟨-R,0,0⟩=⟨-3.5m,0,0⟩\end{array}$ .
  ::从图表的顶端视图中可以看到,A点直接位于来源的左边,因此A点的位置矢量由 RAR,0,03.5m,0,0。

  播放段落

  Point B is located 11m above point A and 7/8 of one turn counter-clockwise is equal to 1/8 of one turn clockwise, so θ = 45 ^o . We can also use the geometry of the system to determine the x and z coordinates of point B: $\begin{array}{r}\stackrel{\to }{r_B}=⟨-R\text{cos}\theta ,R\text{sin}\theta ,H⟩=⟨(-3.5m)\text{cos}{45}^{\circ },(3.5m)\text{sin}{45}^{\circ },11m⟩\end{array}$ $\begin{array}{r}=⟨-2.475m,2.475m,11m⟩\end{array}$
  ::B点位于A点上方11米处,7/8点的反时针值等于1/8点的时钟,因此==45o。我们也可以使用该系统的几何测量来确定B点的x和z坐标:rBQR cos __,R sin __,H(3.5m) cs 45,(3.5m) sin 45,11m2.475m,2.475m,11m__

  播放段落

  The displacement vector between these two points is the vector which obeys the equation: $\begin{array}{r}\stackrel{\to }{\mathrm{△}r}=\stackrel{\to }{r_B}-\stackrel{\to }{r_A}\end{array}$
  ::这两个点之间的移位矢量是符合方程式的矢量:

  播放段落

  $\begin{array}{r}\stackrel{\to }{\mathrm{△}r}=⟨-2.475m,2.475m,11m⟩-⟨-3.5m,0m,0m⟩\end{array}$
  ::2.475m,2.475m,11m 3.5m,0m,0m

  播放段落

  $\begin{array}{r}\stackrel{\to }{\mathrm{△}r}=⟨(-2.475m-(-3.5m)),(2.475m-0m),(11m-0m)⟩=⟨1.025m,2.475m,11m⟩\end{array}$
  :-2.475m-(-3.5m)),(2.475m-0m),(11-0m) 1.025m,2.475m,11m

  播放段落

  Example 5
  ::例5

  播放段落

  Identify the midpoint between points P = (3.7, 8.4, -2.1) and Q = (5.5, -1.9, -8.6).
  ::确定P=(3.7,8.4,-2.1)和Q=(5.5,1.9,-8.6)之间的中点。

  播放段落

  To find the midpoint between two points, determine the average of the two positions.
  ::为在两点之间找到中点,确定两个职位的平均数。

  播放段落

  $\begin{array}{r}M=\left(\frac{1}{2}(3.7+5.5),\frac{1}{2}(8.4+(-1.9)),\frac{1}{2}(-2.1+(-8.6))\right)=\left(\frac{1}{2}(9.2),\frac{1}{2}(6.5)),\frac{1}{2}(-10.7))\right)\end{array}$
  ::M=12(12(3.7+5.5),12(8.4+(-1.9),12(2.1+(-8.6)))=12(12(9),12(6.5),12(-10.7))

  播放段落

  $\begin{array}{r}M=(4.6,3.25,-5.35)\end{array}$
  ::M=(4.6,3.25,-5.35)

  播放段落

  Example 6
  ::例6

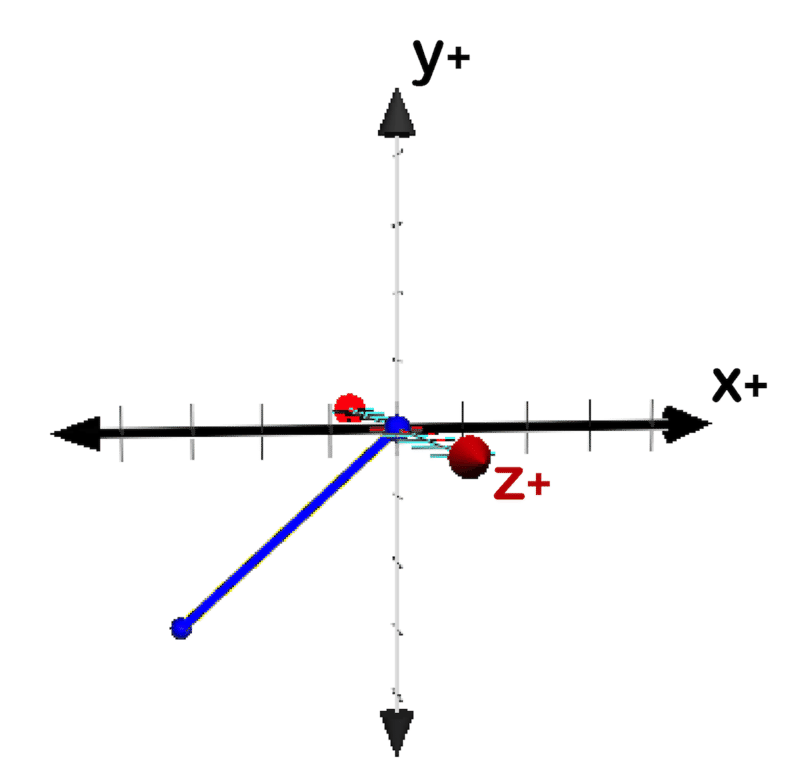
  播放段落

  Draw the three dimensional vector $\begin{array}{r}\stackrel{\to }{A}=3\hat{i}+2\hat{j}+5\hat{k}\end{array}$ .
  ::绘制三维矢量 A3i2j5k。

  播放段落

  I, j and k are unit vectors respectively in the positive direction of the x, y, and z axes.
  ::I、j和k分别是x、y和z轴正方向的单位矢量。

  

  播放段落

  Example 7
  ::例7

  播放段落

  Draw the three dimensional vector $\begin{array}{r}\stackrel{\to }{A}=-3\hat{i}+-4\hat{j}-5\hat{k}\end{array}$ .
  ::绘制三维矢量 A3i4j5k。

  播放段落

  I, j and k are unit vectors respectively in the negative direction of the x, y, and z axes.
  ::I、j和k分别是x、y和z轴负向的单位矢量。

  

  播放段落

  Review
  ::回顾

  播放段落

  Given: initial and final position vectors the coordinate system. Identify the displacement vector or midpoint from the initial to the final position.
  ::给定值: 初始和最终位置矢量协调系统。 确定移位矢量或中点, 从初始到最终位置。

  播放段落
  1. What is the displacement or difference between these two vectors? The initial position vector $\begin{array}{r}\stackrel{\to }{r_i}=⟨0m,0m,0m⟩\end{array}$ and the final position vector $\begin{array}{r}\stackrel{\to }{r_f}=⟨16.1m,7.5m,3m⟩\end{array}$ .
     ::这两个矢量之间的移位或区别是什么?初始位置矢量 ri0m,0m,0m和最终位置矢量 rf16.1m,7.5m,3m。
  播放段落
  2. What is the displacement or difference between these two vectors? The initial position vector $\begin{array}{r}\stackrel{\to }{r_i}=⟨0mi,0mi,0mi⟩\end{array}$ and the final position vector $\begin{array}{r}\stackrel{\to }{r_f}=⟨9.4mi,12.5mi,6.6mi⟩\end{array}$ .
     ::这两个矢量之间的移位或区别是什么?初始位置矢量 ri0mi,0mi,0mi和最终位置矢量 rf9.4mi,12.5mi,6.6mi。
  播放段落
  3. What is the displacement or difference between these two vectors? The initial position vector $\begin{array}{r}\stackrel{\to }{r_i}=⟨5km,3km,8km⟩\end{array}$ and the final position vector $\begin{array}{r}\stackrel{\to }{r_f}=⟨10km,20km,19km⟩\end{array}$ .
     ::这两种矢量之间的移位或区别是什么? 初始位置矢量 ri5km,3km,8km和最终位置矢量 rf10km,20km,19km。
  播放段落
  4. What is the displacement or difference between these two vectors? The initial position vector $\begin{array}{r}\stackrel{\to }{r_i}=⟨1cm,3cm,1cm⟩\end{array}$ and the final position vector $\begin{array}{r}\stackrel{\to }{r_f}=⟨5.1cm,2cm,5cm⟩\end{array}$ .
     ::这两个矢量之间的移位或区别是什么?初始位置矢量 ri1cm,3cm,1cm和最终位置矢量 rf5.1cm,2cm,5cm。
  播放段落
  5. What is the displacement or difference between these two vectors? The initial position vector $\begin{array}{r}\stackrel{\to }{r_i}=⟨5.6mm,10.2mm,2.2mm⟩\end{array}$ and the final position vector $\begin{array}{r}\stackrel{\to }{r_f}=⟨20.4mm,31.1mm,1.1mm⟩\end{array}$ .
     ::这两种矢量之间的移位或区别是什么?初始位置矢量 ri5.6毫米, 10.2毫米, 2.2毫米 和最终位置矢量 rf20.4毫米, 31.1毫米, 1.1毫米 。
  播放段落
  6. What is the displacement or difference between these two vectors? The initial position vector $\begin{array}{r}\stackrel{\to }{r_i}=⟨1in,2in,3in⟩\end{array}$ and the final position vector $\begin{array}{r}\stackrel{\to }{r_f}=⟨4in,5in,3in⟩\end{array}$ .
     ::这两种矢量之间的移位或区别是什么? 初始位置矢量 ri1in, in, in, 3in 和最终位置矢量 rf4in, 5in, in 。

  播放段落

  Identify the midpoint between points A and B.
  ::确定A点和B点之间的中点。

  播放段落
  7. A = $\begin{array}{r}⟨0m,0m,0m⟩\end{array}$ and B = $\begin{array}{r}⟨16.1m,7.5m,3m⟩\end{array}$
     ::A = 0 m, 0 m, 0 m 和 B + 1610m, 750m, 3m 和 B + 1610m, 750m, 3m
  播放段落
  8. A = $\begin{array}{r}⟨0mi,0mi,0mi⟩\end{array}$ and B = $\begin{array}{r}⟨9.4mi,12.5mi,6.6mi⟩\end{array}$
     ::A=0mi,0mi,0mi和B=9.4mi,12.5mi,6.6mi
  播放段落
  9. A = $\begin{array}{r}⟨5km,3km,8km⟩\end{array}$ and B = $\begin{array}{r}⟨10km,20km,19km⟩\end{array}$
     ::A=5公里,3公里,8公里和B=10公里,20公里,19公里
  播放段落
  10. A = $\begin{array}{r}⟨1cm,3cm,1cm⟩\end{array}$ and B = $\begin{array}{r}⟨5.1cm,2cm,5cm⟩\end{array}$
      ::A=1厘米、3厘米、1厘米和B=5.1厘米、2厘米、5厘米
  播放段落
  11. A = $\begin{array}{r}⟨5.6mm,10.2mm,2.2mm⟩\end{array}$ and B = $\begin{array}{r}⟨20.4m,31.1mm,1.1mm⟩\end{array}$
      ::A=5.6毫米、10.2毫米、2.2毫米和B=20.4毫米、31.1毫米、1.1毫米
  播放段落
  12. A = $\begin{array}{r}⟨1in,2in,3in⟩\end{array}$ and B = $\begin{array}{r}⟨4in,5in,3in⟩\end{array}$
      ::A=#1in,2in,3in和B=#4in,5in,3in

  播放段落

  Draw the three dimensional vector.
  ::绘制三维矢量。

  播放段落
  13. $\begin{array}{r}\stackrel{\to }{A}=3\hat{i}+2\hat{j}+5\hat{k}\end{array}$
      ::啊~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
  播放段落
  14. $\begin{array}{r}\stackrel{\to }{A}=5\hat{i}-3\hat{j}+1\hat{k}\end{array}$
      ::啊~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
  播放段落
  15. $\begin{array}{r}\stackrel{\to }{A}=7\hat{i}+1\hat{j}-4\hat{k}\end{array}$
      ::啊~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
  播放段落
  16. $\begin{array}{r}\stackrel{\to }{A}=-7\hat{i}-4\hat{j}+8\hat{k}\end{array}$
      ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}
  播放段落
  17. $\begin{array}{r}\stackrel{\to }{A}=-4\hat{i}+7\hat{j}-3\hat{k}\end{array}$
      ::A4i7j3k
  播放段落
  18. $\begin{array}{r}\stackrel{\to }{A}=-3\hat{i}-2\hat{j}-5\hat{k}\end{array}$
      ::啊~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。