课程： 13.11 利用r和theta在协调计划中找到点

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节使用 r 和 Theta 在坐标平面中找到点

折叠展开
使用 r 和 Theta 在坐标平面中找到点
Trig Riddle: I am a point. My are $\begin{aligned} (2, 330^{\circ}) \end{aligned}$ . What are my Cartesian coordinates?
::Trig Riddle:我是一个点。我是2,330。我的笛卡尔座标是什么?

Convert Polar Coordinates to Cartesian Coordinates
::将极坐标转换为笛卡尔坐标

Let's look at how to convert Polar coordinates to Cartesian coordinates. This is, essentially, the reverse of the process used to convert Cartesian coordinates to Polar coordinates.
::让我们来看看如何将极地坐标转换为笛卡尔坐标。这基本上是把笛卡尔坐标转换为极地坐标的过程的反方向。

Given the point $\begin{aligned} (6, 120^{\circ}) \end{aligned}$ , let's find the equivalent Cartesian coordinates.
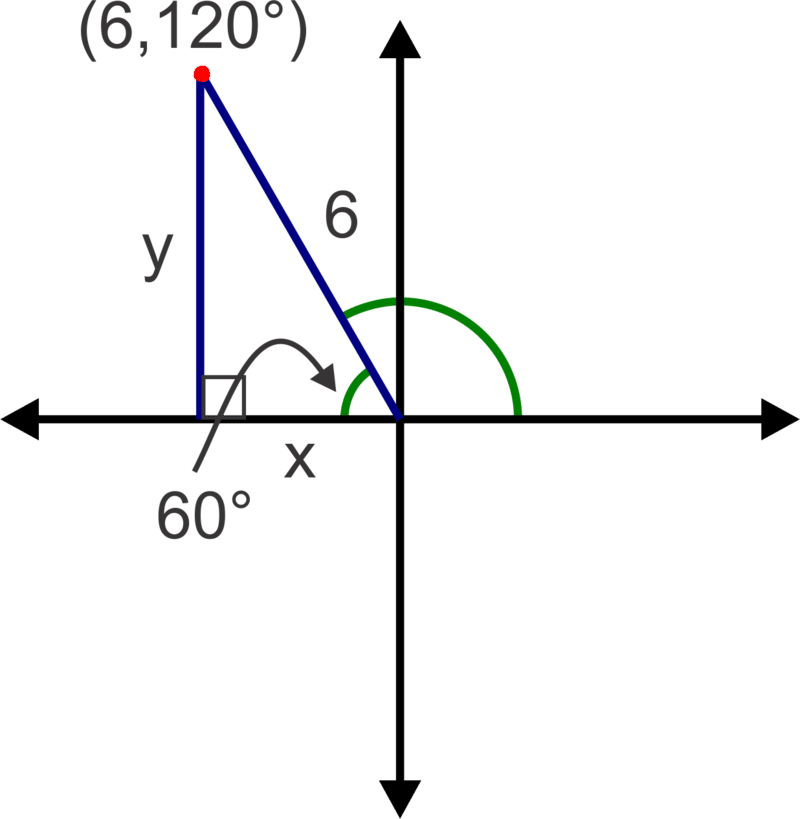
::根据点数(6,120),让我们找到等同的笛卡尔坐标。

First, consider the diagram below and the right triangle formed by a perpendicular segment to the $\begin{aligned} x \end{aligned}$ -axis and hypotenuse equal to the radius. We can find the legs of the right triangle using and thus the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ coordinates of the point.
::首先, 请考虑下图和右三角形, 右三角形由直角段组成, 与 X 轴和下角等值, 等于半径。我们可以使用右三角形的腿, 从而找到点的 x 和 y 坐标。

From the diagram we can see that the reference angle is $\begin{aligned} 60^{\circ} \end{aligned}$ . Now we can use right triangle trigonometry to find $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . In this particular case, we can also use special right triangle ratios or the unit circle .
::从图表中我们可以看到参考角度是 60 。现在我们可以使用右三角三角三角测量来找到 x 和 y。在此特定情况下, 我们也可以使用特殊右三角比或单位圆。

$\begin{aligned} \cos 60^{\circ} & = \frac{x}{6} \sin 60^{\circ} = \frac{y}{6} \\ x & = 6 \cos 60^{\circ} = 6 (\frac{1}{2}) = 3 a n d y = 6 \cos 60^{\circ} = 6 (\frac{\sqrt{3}}{2}) = 3 \sqrt{3} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么?

Since the point is in the second quadrant, the $\begin{aligned} x \end{aligned}$ value should be negative giving the Cartesian coordinates $\begin{aligned} (- 3, 3 \sqrt{3}) \end{aligned}$ .
::由于点位于第二个象限, x 值应为负值,显示笛卡尔坐标(-3,33)。

Recall that every point on the unit circle was $\begin{aligned} (\cos θ, \sin θ) \end{aligned}$ , where $\begin{aligned} θ \end{aligned}$ represented the angle of rotation from the positive $\begin{aligned} x \end{aligned}$ axis and the radius (distance from the origin) was 1. In these problems, our radius varies as we are no longer restricted to the unit circle. In the previous problem , observe that the coordinates $\begin{aligned} (x, y) \end{aligned}$ are essentially $\begin{aligned} (6 \cos 60^{\circ}, 6 \sin 60^{\circ}) \end{aligned}$ where 6 was the radius and $\begin{aligned} 60^{\circ} \end{aligned}$ was the reference angle. We could have used the angle of rotation, $\begin{aligned} 120^{\circ} \end{aligned}$ , and the only difference would be that the cosine ratio would be negative which would automatically make the $\begin{aligned} x \end{aligned}$ coordinate negative. We can generalize this into a rule for converting from Polar coordinates to Cartesian coordinates:
::回顾单位圆的每个点是(cos,sin), 代表正x轴的旋转角度,半径(与原点的距离)为1. 在这些问题上,我们的半径因我们不再局限于单位圆而有所不同。在前一个问题上, 注意坐标( x,y) 基本上( x, y) 6 =半径, 6 =半径, 60 = 6 = 参考角度。我们本可以使用旋转角度, 120 =, 唯一的区别是, 共弦比为负, 这会自动使x坐标为负。我们可以将这一规则概括为从极坐标转换为笛切斯坐标的规则 :

$\begin{aligned} (r, θ) = (r \cos θ, r \sin θ) \end{aligned}$

:r,)=(rcos,rsin)

Now, given the point, $\begin{aligned} (10, - 220^{\circ}) \end{aligned}$ , let's find the Cartesian coordinates.
::现在,考虑到这一点, (10, -220), 让我们找到笛卡尔座标。

Using the rule with $\begin{aligned} r = 10 \end{aligned}$ and $\begin{aligned} θ = 220^{\circ} \end{aligned}$ and the calculator:
::使用 r= 10 和 220 和计算器的规则 :

$\begin{aligned} (10 \cos (- 220^{\circ}), 10 \sin (- 220^{\circ})) = (- 7.66, 6.43) \end{aligned}$

:10cos(-220),10sin(-220)=(-7.66,6.43)

Finally, given the point, $\begin{aligned} (9, \frac{11 π}{6}) \end{aligned}$ , let's find the exact value of the Cartesian coordinates.
::最后,鉴于这一点,(9,11,6),让我们找出笛卡尔座标的确切价值。

This time $\begin{aligned} r = 9 \end{aligned}$ and $\begin{aligned} θ = \frac{11 π}{6} \end{aligned}$ . So, $\begin{aligned} (9 \cos \frac{11 π}{6}, 9 \sin \frac{11 π}{6}) = (9 (\frac{\sqrt{3}}{2}), 9 (- \frac{1}{2})) = (\frac{9 \sqrt{3}}{2}, - \frac{9}{2}) \end{aligned}$ .
::这一次 r=9 和 \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\92\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ -92\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\92\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\92。。\\\\\\\\\\\\\\\\\\\92。。\\

First, draw a diagram. From this diagram we can see that the reference angle is $\begin{aligned} 30^{\circ} \end{aligned}$ . Now we can use right triangle trigonometry to find $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . In this particular case, we can also use special right triangle ratios or the unit circle.
::首先, 绘制图表。从这个图表中, 我们可以看到引用角度是 30\\\\\\ 30\\\ 。现在我们可以使用右三角三角三角测量来查找 x 和 y。在此特定情况下, 我们也可以使用特殊的右三角比或单位圆。

$\begin{aligned} \cos 30^{\circ} & = \frac{x}{2} \sin 30^{\circ} = \frac{y}{2} \\ x & = 2 \cos 30^{\circ} = 2 (\frac{\sqrt{3}}{2}) = \sqrt{3} a n d y = 2 \sin 30^{\circ} = 2 (\frac{1}{2}) = 1 \end{aligned}$

::30x2 sin 30Y2x=2cos 30302(32) 3和y=2sin}3022(12)=1

Since the point is in the fourth quadrant, the $\begin{aligned} y \end{aligned}$ value should be negative giving the Cartesian coordinates $\begin{aligned} (\sqrt{3}, - 1) \end{aligned}$ .
::由于点在第四象限,Y值应为负值,表示笛卡尔坐标(3,-1)。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the Cartesian coordinates for a point whose Polar coordinates are $\begin{aligned} (2, 330^{\circ}) \end{aligned}$ .
::早些时候,有人要求你找到笛卡尔座标,以找到极地座标(2 330)所在的点。

First draw a diagram. From the diagram we can see that the reference angle is $\begin{aligned} 30^{\circ} \end{aligned}$ . Now we can use right triangle trigonometry to find $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . In this particular case, we can also use special right triangle ratios or the unit circle.
::首先绘制图表。从图表中我们可以看到参考角度是 30\\\\\\\\\\\\\ n现在我们可以使用右三角三角三角测量来找到 x和 y。在此特定情况下, 我们也可以使用特殊的右三角三角比或单位圆。

$\begin{aligned} \cos 30^{\circ} & = \frac{x}{2} \sin 30^{\circ} = \frac{y}{2} \\ x & = 2 \cos 30^{\circ} = 2 (\frac{\sqrt{3}}{2}) = \sqrt{3} a n d y = 2 \cos 30^{\circ} = 2 (\frac{1}{2}) = 1 \end{aligned}$

::30x2 sin 30Y2x=2cos 30302(32) 3和y=2cos 302(12)=1

Since the point is in the fourth quadrant, the $\begin{aligned} y \end{aligned}$ value should be negative giving the Cartesian coordinates $\begin{aligned} (\sqrt{3}, - 1) \end{aligned}$ .
::由于点在第四象限,Y值应为负值,表示笛卡尔坐标(3,-1)。

Example 2
::例2

Use your calculator to find the Cartesian coordinates equivalent to the Polar coordinates $\begin{aligned} (11, 157^{\circ}) \end{aligned}$ .
::使用计算器找到与极地坐标(11,157)相等的笛卡尔坐标(11,157)。

$\begin{aligned} (11 \cos 157^{\circ}, 11 \sin 157^{\circ}) \approx (- 10.13, 4.30) \end{aligned}$
:11cos157,11sin157)(-1013.4.30)

Example 3
::例3

Find the exact value of the Cartesian coordinates equivalent to the Polar coordinates $\begin{aligned} (8, 45^{\circ}) \end{aligned}$ .
::找到相当于极地坐标(8,45)的笛卡尔座标的准确值。

$\begin{aligned} (8 \cos 45^{\circ}, 8 \sin 45^{\circ}) = (8 (\frac{\sqrt{2}}{2}), 8 (\frac{\sqrt{2}}{2})) = (4 \sqrt{2}, 4 \sqrt{2}) \end{aligned}$
:8cos45,8sin45) =(8(22),8(22) =(42,42)

Example 4
::例4

Find the exact value of the Cartesian coordinates equivalent to the Polar coordinates $\begin{aligned} (5, - \frac{π}{2}) \end{aligned}$ .
::找到相当于极地坐标(5,2)的笛卡尔座标的准确值。

$\begin{aligned} (5 \cos (- \frac{π}{2}), 5 \sin (- \frac{π}{2})) = (5 (0), 5 (- 1)) = (0, - 5) \end{aligned}$
:5cos(2),5sin(2)) =(5(0),5(-1) =(0),5(-5) =(0)

Review
::回顾

Use your calculator to find the Cartesian coordinates equivalent to the following Polar coordinates. Give your answers rounded to the nearest hundredth.
::使用您的计算器找到与以下极坐标相等的笛卡尔座标。将答案四舍五入到最接近的一百位。

$\begin{aligned} (13, 38^{\circ}) \end{aligned}$

$\begin{aligned} (25, - 230^{\circ}) \end{aligned}$

$\begin{aligned} (17, 345^{\circ}) \end{aligned}$

$\begin{aligned} (2, 140^{\circ}) \end{aligned}$

$\begin{aligned} (7, \frac{2 π}{5}) \end{aligned}$

$\begin{aligned} (9, 2.98) \end{aligned}$

$\begin{aligned} (3, - 5.87) \end{aligned}$

$\begin{aligned} (10, \frac{13 π}{7}) \end{aligned}$

Find the exact value Cartesian coordinates equivalent to the following Polar coordinates.
::找到与以下极地坐标相等的笛卡尔座标的准确值。

$\begin{aligned} (5, \frac{π}{3}) \end{aligned}$

$\begin{aligned} (6, - \frac{π}{4}) \end{aligned}$

$\begin{aligned} (12, \frac{5 π}{6}) \end{aligned}$

$\begin{aligned} (7, π) \end{aligned}$

$\begin{aligned} (11, 2 π) \end{aligned}$

$\begin{aligned} (14, \frac{4 π}{3}) \end{aligned}$

$\begin{aligned} (27, \frac{3 π}{4}) \end{aligned}$

$\begin{aligned} (40, - \frac{5 π}{6}) \end{aligned}$

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

使用 r 和 Theta 在坐标平面中找到点

Convert Polar Coordinates to Cartesian Coordinates ::将极坐标转换为笛卡尔坐标

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Convert Polar Coordinates to Cartesian Coordinates
::将极坐标转换为笛卡尔坐标

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)