Course: 5.7 空间飞机 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 空间飞机

Collapse Expand
空间飞机
Orlando is building a coffee table for his mother. He has the round surface cut and sanded and is ready to attach the legs. As he tries a few different heights, he notices that unless the spot on the floor is really flat, and he is extremely careful to make the legs exactly the same length, the table is unsteady and wobbles annoyingly.
::奥兰多正在为他的母亲建一个咖啡桌。他有圆形表面切割和沙子,准备绑住腿。当他尝试几处不同的高度时,他注意到,除非地板上的位置是平的,而且他非常小心地使腿的长度完全相同,否则,桌子是不稳定的,摇晃的,令人烦恼的。

How can Orlando ensure that the table remains stable, even if the floor is not entirely flat where his mom decides to put it?
::奥兰多如何能确保桌子保持稳定,即使地板不是完全平的,而他的母亲却决定把桌子放在地板上?

Planes in Space
::空间飞机

Vectors can be used to identify directions in space and also the orientation of a plane by identifying the direction perpendicular to that plane. In this section we will look at that calculation in reverse. Rather than determining the normal vector to a plane using two vectors which lie in that plane, we will be using the normal vector to determine the equation for the plane itself. We will also use the normal vectors to determine the intersection angle between any pair of planes.
::矢量可用于识别空间方向和飞机方向,方法是识别与该平面垂直的方向。在本节中,我们将反向查看这一计算结果。我们不是使用该平面上的两个矢量来确定平面上的正常矢量,而是使用正常矢量来确定平面本身的方程。我们还将使用正常矢量来确定任何一对平面之间的交叉角度。

Intercept Form
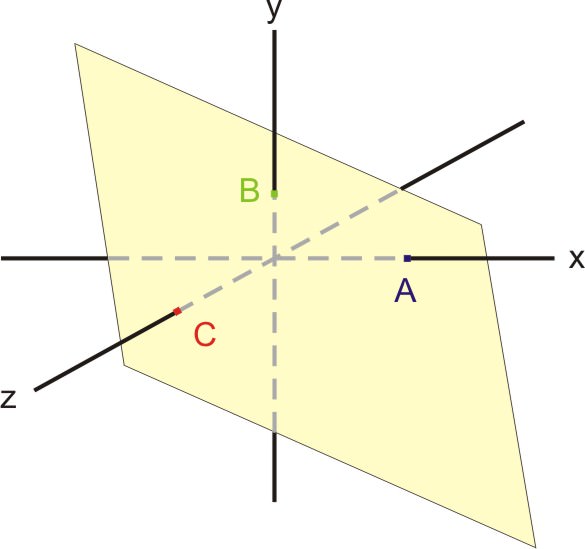
::拦截形式

The diagram below shows a plane that crosses all three coordinate axes. Points A, B, and C are the locations where the plane crosses each of the coordinate axes, called intercepts . Their locations are given by A = (a, 0, 0), B = (0, b, 0), and C = (0, 0, c). The line segments AB , BC , and CA all lie in the plane. Furthermore, segment AB is a portion of the line of intersection between this plane and the x-y axis; segment BC is a portion of the line of intersection between this plane and the y-z axis; and segment CA is a portion of the line of intersection between this plane and the z-x axis.
::下图显示一个横跨所有三个坐标轴的平面。 A、 B和 C点是该平面跨过每个坐标轴的位置,称为拦截。其位置由 A = (a, 0, 0, 0, B = 0, B = 0, b, 0 ) 和 C = (0, 0, c) 给出。线段AB、 BC 和 CA 全部在平面上。此外, 分段AB 是此平面和 X- y 轴之间交叉线的一部分; BC 段是此平面和 y- Z 轴之间交叉线的一部分; CA 段是此平面和 Z- X 轴之间交叉线的一部分。

The intercept form of the equation for a plane is given by
::飞机方程的截截截形式由

$\begin{aligned} 1 = \frac{x}{a} + \frac{y}{b} + \frac{z}{c} \end{aligned}$
::1=xa+yb+zc =xa+yb+zc =xa+yb+zc =xa+yb+zc

Using a Normal Vector
::使用普通矢量

Another way to specify a plane is to know two vectors within the plane. Recall that if two vectors lie in the same plane, the normal to that plane can be found using the of the two vectors. Sometimes we are given the equations of the vectors themselves. Sometimes, however, we are only given a set of points that lie on the plane. If we know three points that lie on the plane, we can use the method developed when looking at to find equations for the vectors between those points and then use those vectors to identify the plane. We only need three points to accomplish this task.
::指定一个平面的另一种方式是知道在平面上的两个矢量。回顾如果两个矢量位于同一个平面上, 就可以用两个向量本身的方程式找到该平面的正常值。有时我们得到矢量本身的方程式。然而, 有时我们只得到一连串在平面上的点数。如果我们知道飞机上有三个点, 我们就可以使用开发的方法来寻找这两个点之间的矢量方程式, 然后用这些矢量来识别该平面。我们只需要三个点来完成这个任务。

Since the normal to the plane is, by definition, perpendicular to all possible vectors within a plane and since the dot product of two vectors is equal to zero for any two perpendicular vectors, we can define a plane in terms of the dot product of the normal vector with any vector, $\begin{aligned} \vec{v} \end{aligned}$ , within the plane:
::由于根据定义,飞机的正常值与飞机内所有可能的矢量是垂直的,而且由于两个矢量的圆点产物在任何两个垂直矢量中等于零,我们可以用正常矢量的圆点产物来定义一个平面,在平面内的任何矢量,v:

$\begin{aligned} \vec{n} \times \vec{v} = 0 \end{aligned}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不,不

Which we can also write as
::我们也可以写作为

$\begin{aligned} ⟨ n_{x}, n_{y}, n_{z} ⟩ \times ⟨ (x - x_{0}), (y - y_{0}), (z - z_{0}) ⟩ = 0 \end{aligned}$
::nx,ny,nznz(x-x0),(y-y0),(z-z0)0

If we compute the dot product, we obtain another equation which specifies the plane in terms of the normal vector and two points on the plane, ( x , y , z ) and ( x ₀ , y ₀ , z ₀ ).
::如果我们计算点产品,我们就会获得另一个方程,以正常矢量和平面上两点(x、y、z)和(x0、y0、z0)来指定平面的正向量和平面上两点。

n _x ( x - x ₀ ) + n _y ( y - y ₀ ) + n _z ( z - z ₀ ) = 0
::nx (x - x0) + ny (y - y0) + z (z - z0) = 0

This equation is frequently written as
::此等式经常被写为

n _x x + n _y y + n _z z + d = 0
::nxx + Nyy + nzz + d = 0

Where
::何处处

d = - n _x x _o - n _y y _o - n _z z _o
:d) = -nxxo -nyyo - nzzo

and the intercepts of the plane with the x, y, and z axes are given by:
::用x、y和z轴拦截的飞机的截击由下列人员提供:

$\begin{aligned} a = - \frac{d}{n_{x}}, b = - \frac{d}{n_{y}}, \end{aligned}$ and $\begin{aligned} c = - \frac{d}{n_{z}} \end{aligned}$
::adnx, bdny, 和 cdnz

If you only have the normal vector and one point on the plane, first determine the of the position vector of that point onto the normal vector using the dot product. Then you will have the locations of two points on the plane and can use the normal and two points method described above.
::如果您在平面上只有正常矢量和一分, 请使用点产品先确定该点在正常矢量上的位置矢量。然后您将拥有平面上两个点的位置, 并且可以使用上文描述的正常和两个点的方法。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Orlando, who is making a table for his mother.
::早些时候,你被问及奥兰多的问题, 奥兰多正在为他的母亲做桌子。

How can he ensure that the table remains stable, even if the floor is not entirely flat where his mom decides to put it?
::他如何能确保桌子保持稳定,即使地板不是完全平的,而他的妈妈却决定把桌子放在地板上?

Recall from the lesson that any plane can be defined by three points. If Orlando makes the table with only three legs, then the endpoints of each leg will define a stable plane for the table to sit on. Even if the plane defined by the leg endpoints is not exactly parallel to the average plane of the floor across the entire room, the table itself will remain stable.
::从任何飞机都可以用三个点来定义。如果奥兰多的桌子只有三条腿,那么每条腿的端点将确定一个稳定的平面,供桌子坐坐。即使腿端点所定义的平面与整个房间的平面平均平面并不完全平行,但表本身也会保持稳定。

Example 2
::例2

Find the intercepts of the plane given by the equation 3 x + 5 y - 2 z - 4 = 0.
::查找方程式 3x + 5y - 2z - 4 = 0 给出的飞机拦截量。

Rewrite the equation of the plane in the format of the intercept form of the plane equation.
::重写平面方程式的方程式以截取方程式的形式重写平面方程式。

3 x + 5 y - 2 z = 4
::3x + 5y - 2z = 4

$\begin{aligned} 1 = \frac{3}{4} x + \frac{5}{4} y + \frac{- 2}{4} z \end{aligned}$
::1=34x+54y24z

$\begin{aligned} a = \frac{4}{3}, b = \frac{4}{5} \end{aligned}$ , and $\begin{aligned} c = \frac{4}{- 2} = - 2 \end{aligned}$ . Thus the intercepts of this plane are
::a=43, b=45, c=4 -2 *2。因此,这架飞机的拦截是

$\begin{aligned} (\frac{4}{3}, 0, 0), (0, \frac{4}{5}, 0) \end{aligned}$ , and $\begin{aligned} (0, 0, - 2) \end{aligned}$ .
:43,0,0,0,(0,45,0)和(0,0,02)。

Example 3
::例3

A plane has intersections at (12, 0, 0), (0, 6, 0), and (0, 0, 4). Write the equation of the plane.
::飞机在12、0、0、0(0、6、0)和(0、0、4)处有交叉点。

$\begin{aligned} 1 = \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = \frac{x}{12} + \frac{y}{6} + \frac{z}{4} \end{aligned}$ or $\begin{aligned} 12 = x + 2 y + 3 z \end{aligned}$
::1=xa+yb+zc=x12+y6+z4或12=x+2y+3z

Example 4
::例4

Use the equation 3 x + 5 y - 2 z - 4 = 0 to determine the normal unit-vector to that plane.
::使用方程 3x + 5y - 2z - 4 = 0 确定该平面的正常单位矢量。

Comparing this equation to n _x x + n _y y + n _z z + d = 0, we can see that $\begin{aligned} \vec{n} = ⟨ 3, 5, - 2 ⟩ \end{aligned}$ . To find the unit normal vector , find the magnitude of this normal vector and divide each component by the magnitude.
::用 nxx + nny + nzz + nzz + d = 0来比较这个方程,我们可以看到 n 3,5, - 2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ nxxxxxxx\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

$\begin{aligned} | \vec{n} | = \sqrt{n_{x}^{2} + n_{y}^{2} + n_{z}^{2}} = \sqrt{3^{2} + 5^{2} + (- 2)^{2}} = \sqrt{38} \end{aligned}$
::nx2+ny2+nz2=32+52+(-2)2=38

$\begin{aligned} \hat{n} = ⟨ \frac{3}{\sqrt{38}}, \frac{5}{\sqrt{38}}, \frac{- 2}{\sqrt{38}} ⟩ \end{aligned}$
::n338,538,-238

Example 5
::例5

The three points P = (3, 7, 2), Q = (1, 4, 3), and R = (2, 3, 4) define a plane. Determine the equation of the plane.
::三点P = (3, 7, 2),Q = (1, 4, 3),R = (2, 3, 4) 定义一平面。确定平面的方程。

First find the vectors between two pairs of the points.
::首先在两对点之间找到矢量。

$\begin{aligned} \vec{P Q} = ⟨ (Q_{x} - P_{x}), (Q_{y} - P_{y}), (Q_{z} - P_{z}) ⟩ = ⟨ (1 - 3), (4 - 7), (3 - 2) ⟩ = \end{aligned}$ $\begin{aligned} ⟨ - 2, - 3, 1 ⟩ \end{aligned}$
::P(Qx-Px),(Qy-Py),(Qz-Pz) (1-3),(4-7),(3-2),(2)-3,1

$\begin{aligned} \vec{P R} = ⟨ (R_{x} - P_{x}), (R_{y} - P_{y}), (R_{z} - P_{z}) ⟩ = ⟨ (2 - 3), (3 - 7), (4 - 2) ⟩ = \end{aligned}$ $\begin{aligned} ⟨ - 1, - 4, 2 ⟩ \end{aligned}$
::PR(Rx-Px),(Ry-Py),(Rz-Pz) (2-3),(3-7),(4-2),(1) - 4,2

The cross product of these two vectors is normal to the plane.
::这两个矢量的交叉产物对飞机来说是正常的。

$\begin{aligned} \vec{P Q} \times \vec{P R} = ⟨ (P Q_{y} P R_{z} - P Q_{z} P R_{y}), (P Q_{z} P R_{x} - P Q_{x} P R_{z}), (P Q_{x} P R_{y} - P Q_{y} P R_{x}) ⟩ \end{aligned}$
::P(PQyPRz-PQzPRy),(PQzPRx-PQxPRz),(PQxPRy-PQPRx)

$\begin{aligned} \vec{P Q} \times \vec{P R} = ⟨ [(- 3 \cdot 2) - (1 \cdot - 4)], [(1 \cdot - 1) - (- 2 \cdot 2)], [(- 2 \cdot - 4) - (- 1 \cdot - 3)] ⟩ \end{aligned}$
::PP[(-32)-(14)],[(11)-(-22),[(-24)-(-13)]

$\begin{aligned} \vec{n} = \vec{P Q} \times \vec{P R} = ⟨ [(- 6) - (- 4)], [(- 1) - (- 4)], [(8) - (3)] ⟩ = ⟨ - 2, 3, 5 ⟩ \end{aligned}$
:-6)-(-4),[-1)-(-4)],[(8)-(3)-],[2,3,5]

This normal vector and one of the points will give an equation for the plane.
::这个正常的向量和一个点将给平面一个方程

n _x ( x - P _x ) + n _y ( y - P _y ) + n _z ( z - P _z ) = 0
::nx (x - Px) + ny (y - Py) + z (z - Pz) = 0

-2( x - 3) + 3( y - 7) + 5( z - 2) = 0
::-2(x-3) + 3(y-7) + 5(z-2) = 0

-2 x + 3 y + 5 z + (6 - 21 - 10) = 0
::-2x + 3y + 5z + 5z + (6 - 21 - 10) = 0

-2 x + 3 y + 5 z - 25 = 0
::-2x + 3y + 5z - 25= 0

Example 6
::例6

Rewrite the equation of the plane 7 x + 3 y + z + 12 = 0 in intercept form.
::重写 7x + 3y + z + 12 = 0 的截取式平面的方程式。

The equation $\begin{aligned} 1 = \frac{x}{a} + \frac{y}{b} + \frac{z}{c} \end{aligned}$ must be true for all points on a plane. Therefore, we should first rearrange 7 x + 3 y + z + 12 = 0 into the form $\begin{aligned} 1 = \frac{x}{a} + \frac{y}{b} + \frac{z}{c} \end{aligned}$ .
::等式 1 = Xa+yb+zc 必须是适用于平面上所有点的。因此, 我们应该首先将 7x + 3y + z + 12 = 0 改为 1= Xa+yb+zc 。

7 x + 3 y + z = -12
::7x + 3y + z = -12

$\begin{aligned} \frac{7}{- 12} x + \frac{3}{- 12} y + \frac{1}{- 12} z = 1 \end{aligned}$
::7-12x+3-12y+1-12z=1

Therefore, $\begin{aligned} a = \frac{- 12}{7}, b = \frac{- 12}{3} = - 4 \end{aligned}$ , and $\begin{aligned} c = \frac{- 12}{1} = - 12 \end{aligned}$ and the position vectors of the three intercepts are $\begin{aligned} \vec{A} = ⟨ - 1.714, 0, 0 ⟩, \vec{B} = ⟨ 0, - 4, 0 ⟩ \end{aligned}$ , and $\begin{aligned} \vec{C} = ⟨ 0, 0, - 12 ⟩ \end{aligned}$
::因此,a127,b1234,和c12112 以及这3个拦截器的方位为A1.714,00.0,B0,4,0,和C0,0,-12。

Example 7
::例7

Determine the equation for the unit vector which is perpendicular to the plane, 7 x + 3 y + z + 12 = 0.
::确定与平面垂直的单位矢量的方程式, 7x + 3y + z + 12 = 0。

Comparing this equation to $\begin{aligned} n_{x} x + n_{y} y + n_{z} z + d = 0 \end{aligned}$ , we can see that $\begin{aligned} \vec{n} = ⟨ 7, 3, 1 ⟩ \end{aligned}$
::将这个方程比作 nxx+nyy+nzz+d=0, 我们可以看到n7,3,1

$\begin{aligned} \hat{n} = \frac{\vec{n}}{| \vec{n} |} = \frac{⟨ n_{x}, n_{y}, n_{z} ⟩}{\sqrt{n_{x}^{2} + n_{y}^{2} + n_{z}^{2}}} = \frac{⟨ 7, 3, 1 ⟩}{\sqrt{(7)^{2} + (3)^{2} + (1)^{2}}} = \frac{⟨ 7, 3, 1 ⟩}{\sqrt{49 + 9 + 1}} \end{aligned}$
::nnnnux,ny,nznx2+ny2+nz2+nz2+7,3,1(7)2+(3)2+(1)2+7,3,149+9+1

$\begin{aligned} = \frac{⟨ 7, 3, 1 ⟩}{\sqrt{59}} = ⟨ \frac{7}{\sqrt{59}}, \frac{3}{\sqrt{59}}, \frac{1}{\sqrt{59}} ⟩ \end{aligned}$

Example 8
::例8

A plane is defined by three points having position vectors $\begin{aligned} \vec{r_{1}} = ⟨ 1, 0, - 1 ⟩, \vec{r_{2}} = ⟨ 2, 4, 6 ⟩ \end{aligned}$ , and $\begin{aligned} \vec{r_{3}} = ⟨ - 3, 7, 5 ⟩ \end{aligned}$ . Determine the components of the unit vector which is perpendicular to the plane passing through those points.
::平面由具有向量位置的三点确定,即向量1°1°0,0°1°,r2°2°2,4°6°,和r3°3°3,7°5°。确定与通过这些点的平面垂直的单位向量的组件。

The cross-product determines the direction perpendicular to a pair of vectors. Therefore we can use these three points to define two vectors in the same plane. The vector from point 1 to point 2 is given by subtracting vector 2 from vector 1:
::交叉产品决定与一对矢量的垂直方向。因此, 我们可以使用这三个点来定义同一平面上的两个矢量。从1点到2点的矢量是通过从矢量 1 中减去矢量 2 来给定的。

$\begin{aligned} \vec{r_{1 - 2}} = \vec{r_{1}} - \vec{r_{2}} = ⟨ 1, 0, - 1 ⟩ - ⟨ 2, 4, 6 ⟩ = ⟨ 1 - 2, 0 - 4, - 1 - 6 ⟩ = ⟨ - 1, - 4, - 7 ⟩ \end{aligned}$
::1-2_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Likewise, the vector from point 1 to point 3 is given by subtracting vector 3 from vector 1:
::同样,从第1点到第3点的矢量通过从第1点减去第1点的矢量3而得出:

$\begin{aligned} \vec{r_{1 - 3}} = \vec{r_{1}} - \vec{r_{3}} = ⟨ 1, 0, - 1 ⟩ - ⟨ - 3, 7, 5 ⟩ = ⟨ 1 - (- 3), 0 - 7, - 1 - 5 ⟩ = \end{aligned}$ $\begin{aligned} ⟨ 4, - 7, - 6 ⟩ \end{aligned}$
::-1,0,-1,3,7,5,1-(-3,3,0-7,7,5-)-7,-1,5,4,7,6--

Now we can use the cross-product of the two vectors in the plane to determine a vector which is perpendicular to that plane,
::现在我们可以使用飞机上两个矢量的交叉产品来确定一个与飞机垂直的矢量

$\begin{aligned} \vec{n} = \vec{r_{1 - 2}} \times \vec{r_{1 - 3}} = ⟨ (r_{1 - 2 y} r_{1 - 3 z} - r_{1 - 2 z} r_{1 - 3 y}), (r_{1 - 2 z} r_{1 - 3 x} - r_{1 - 2 x} r_{1 - 3 z}), (r_{1 - 2 x} r_{1 - 3 y} - r_{1 - 2 y} r_{1 - 3 x}) ⟩ \end{aligned}$
::nr1-21-3(r1-2yr1-3z-r1-2zr1-2zr1-3y,r1-2zr1-3x-r1-2xr1-3z,r1-2xr1-3z,r1-2xr1-3y-r1-2r1-3yr1-3x)

$\begin{aligned} \vec{n} = \vec{r_{1 - 2}} \times \vec{r_{1 - 3}} = ⟨ ((- 4) (- 6) - (- 7) (- 7)), ((- 7) (4) - (- 1) (- 6)), ((- 1) (- 7) - (- 4) (4)) ⟩ \end{aligned}$
::nr1-2r1-3(-4)-6)-(-7)-7),(-7)(4)-(-1)-6),(-1)-7)-(-4)-(-4)(4)

$\begin{aligned} \vec{n} = \vec{r_{1 - 2}} \times \vec{r_{1 - 3}} = ⟨ ((24) - (49), ((- 28) - (6)), ((7) - (- 16)) ⟩ = ⟨ - 25, - 34, 23 ⟩ \end{aligned}$
:24)-(49),(28)-(6),(7)-(16))-(25)-34,23

Now use the definition of the unit vector to complete the problem.
::现在使用单位矢量的定义来完成问题。

$\begin{aligned} \hat{n} = \frac{\vec{n}}{| \vec{n} |} = \frac{⟨ n_{x}, n_{y}, n_{z} ⟩}{\sqrt{n_{x}^{2} + n_{y}^{2} + n_{z}^{2}}} = \frac{⟨ - 25, - 34, 23 ⟩}{\sqrt{(- 25)^{2} + (- 34)^{2} + (23)^{2}}} \end{aligned}$
::nnnnnux,ny,nznx2+ny2+Nz2+Nz2}25,-34,23(-25)2+(-34)2+(-23)2

$\begin{aligned} = \frac{⟨ - 25, - 34, 23 ⟩}{\sqrt{625 + 1156 + 529}} = \frac{⟨ - 25, - 34, 23 ⟩}{\sqrt{2310}} \end{aligned}$

$\begin{aligned} \hat{n} = \frac{\vec{n}}{| \vec{n} |} = \frac{⟨ - 25, - 34, 23 ⟩}{48.06} = ⟨ - 0.5202, - 0.7074, 0.4785 ⟩ \end{aligned}$
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

Example 9
::例9

Determine the components of the unit vector which is perpendicular to the plane 12 x + 23 y + 14 z - 5 = 0.
::确定与平面12x + 23y + 14z - 5 = 0 垂直的单位矢量的组件。

Comparing this equation to $\begin{aligned} n_{x} x + n_{y} y + n_{z} z + d = 0 \end{aligned}$ , we can see that $\begin{aligned} \vec{n} = ⟨ 12, 23, 14 ⟩ \end{aligned}$ .
::将这个方程比作 nxx+nyy+nzz+d=0, 我们可以看到n12, 23, 14。

Now we can use the definition of the unit vector to complete the problem.
::现在我们可以使用单位矢量的定义来解决这个问题。

$\begin{aligned} \hat{n} = \frac{\vec{n}}{| \vec{n} |} = \frac{⟨ n_{x}, n_{y}, n_{z} ⟩}{\sqrt{n_{x}^{2} + n_{y}^{2} + n_{z}^{2}}} = \frac{⟨ 12, 23, 14 ⟩}{\sqrt{12^{2} + 23^{2} + 14^{2}}} = \frac{⟨ 12, 23, 14 ⟩}{\sqrt{869}} \end{aligned}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}Nánnnnx2+ny2+ny2+Nz2+Nz2+12,23,14122+232+14212,23,14869 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

$\begin{aligned} = \frac{⟨ 12, 23, 14 ⟩}{29.5} = ⟨ \frac{12}{29.5}, \frac{23}{29.5}, \frac{14}{29.5} ⟩ \end{aligned}$

Review
::回顾

Given the following intersections, write the equation of the plane.
::根据下面的交叉点写下飞机的方程

$\begin{aligned} (7, 0, 0), (0, 3, 0) \end{aligned}$ and $\begin{aligned} (0, 0, 19) \end{aligned}$
:7,0,0,0,(0,03,0)和(0,0,19)

$\begin{aligned} (2, 0, 0), (0, 8, 0) \end{aligned}$ and $\begin{aligned} (0, 0, 5) \end{aligned}$
:2,0,0,0,0,8,0)和(0,0,0,5)

$\begin{aligned} (13, 0, 0), (0, 21, 0) \end{aligned}$ and $\begin{aligned} (0, 0, 17) \end{aligned}$
:13,0,0,0,(0,21,0)和(0,0,0,17)

$\begin{aligned} (5, 0, 0), (0, 1, 0) \end{aligned}$ and $\begin{aligned} (0, 0, 2) \end{aligned}$
:5,0,0,0,(0,0,0,0)和(0,0,0)

$\begin{aligned} (27, 0, 0), (0, 12, 0) \end{aligned}$ and $\begin{aligned} (0, 0, 18) \end{aligned}$
:27,0,0,0,(0,12,0)和(0,0,0,18)

Find the intercepts of the plane given the following equations.
::根据以下方程式找到飞机的拦截数据

$\begin{aligned} 3 x + 2 y + z - 6 = 0 \end{aligned}$
::3x+2y+z-6=0

$\begin{aligned} 1 x - 7 y - z + 10 = 0 \end{aligned}$
::1x-7y-z+10=0

$\begin{aligned} - 2 x + 9 y + 4 z - 1 = 0 \end{aligned}$
::− 2x+9y+4z-1=0

$\begin{aligned} 6 x - 11 y + 2 z + 3 = 0 \end{aligned}$
::6-11y+2z+3=0

$\begin{aligned} - 2 x + 5 y + 5 z + 6 = 0 \end{aligned}$
::− 2x+5y+5z+6=0

Use the given equations to determine the normal unit-vector to that plane.
::使用给定方程确定该平面的正常单位矢量。

$\begin{aligned} 7 x + 5 y - 1 z - 10 = 0 \end{aligned}$
::7x+5y-1z-10=0

$\begin{aligned} 4 x - 13 y + 5 z - 3 = 0 \end{aligned}$
::4-13y+5z-3=0

$\begin{aligned} - 8 x + 7 y + 2 z + 5 = 0 \end{aligned}$
::-8x+7y+2z+5=0

$\begin{aligned} 10 x + 3 y - z - 2 = 0 \end{aligned}$
::10x+3y-z-2=0

$\begin{aligned} - 1 x - 2 y + 7 z + 16 = 0 \end{aligned}$
::− 1x-2y+7z+16=0

Determine the equation of the planes below using the three points given.
::使用给定的三点确定下方平面的方程。

$\begin{aligned} P = (3, 6, 9), Q = (9, 6, 3) \end{aligned}$ and $\begin{aligned} R = (6, - 9, 9) \end{aligned}$
::P=(3,6,9,9)(9,6,3)和R=(6,9,9)

$\begin{aligned} P = (1, - 7, 2), Q = (4, 2, 9) \end{aligned}$ and $\begin{aligned} R = (3, - 5, 1) \end{aligned}$
::P=(1, - 7,2, (4, 2, 9) 和 R= (3, -5, 1)

$\begin{aligned} P = (3, 8, 10), Q = (- 2, 5, 8) \end{aligned}$ and $\begin{aligned} R = (7, 4, 8) \end{aligned}$
::P=(3,8,10)、(-2,5,8)和R=(7,4,8)

$\begin{aligned} P = (9, - 1, 4), Q = (6, 2, - 8) \end{aligned}$ and $\begin{aligned} R = (12, 9, 10) \end{aligned}$
::P=(9,-1,4), (6,2,-8)和R=(12,9,10)

$\begin{aligned} P = (5, 8, - 9), Q = (- 5, 3, 9) \end{aligned}$ and $\begin{aligned} R = (10, 4, - 6) \end{aligned}$
::P=(5,5,8,-9)(-5,3,9)和R=(10,4,-6)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

空间飞机

Planes in Space ::空间飞机

Intercept Form ::拦截形式

Using a Normal Vector ::使用普通矢量

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

= ⟨ 7 , 3 , 1 ⟩ 59 = ⟨ 7 59 , 3 59 , 1 59 ⟩

Example 8 ::例8

Example 9 ::例9

Review ::回顾

Review (Answers) ::回顾(答复)

Planes in Space
::空间飞机

Intercept Form
::拦截形式

Using a Normal Vector
::使用普通矢量

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

$\begin{aligned} = \frac{⟨ 7, 3, 1 ⟩}{\sqrt{59}} = ⟨ \frac{7}{\sqrt{59}}, \frac{3}{\sqrt{59}}, \frac{1}{\sqrt{59}} ⟩ \end{aligned}$

Example 8
::例8

Example 9
::例9

Review
::回顾

Review (Answers)
::回顾(答复)