14.6 三角特征介绍

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 特里格特征介绍

  Collapse Expand

  特里格特征介绍

  播放段落

  You are given a list of Trig Identities. One of those identities is $\begin{array}{r}\cos (-\theta )=\cos \theta \end{array}$ . Prove this identity without graphing.
  ::您被给出了 Trig 身份列表。 其中之一是 cos = cos。 无需图形化来证明此身份 。

  播放段落

  Trigonometric Identities
  ::三角度数特征

  播放段落

  Trigonometric identities are true for any value of $\begin{array}{r}x\end{array}$ (as long as the value is in the domain). You have learned about secant, cosecant , and cotangent , which are all reciprocal functions of sine, cosine and tangent. These functions can be rewritten as the because they are always true.
  ::三角特性对于 x 的任何值都是真实的( 只要值在域内 ) 。 您已经学会了松散、 共生和余切, 它们是正弦、 共生和正切的对等函数。 这些函数可以被重写为真实, 因为它们总是真实的 。

  播放段落

  Reciprocal Identities: $\begin{array}{r}\csc \theta =\frac{1}{\sin \theta }\sec \theta =\frac{1}{\cos \theta }\cot \theta =\frac{1}{\tan \theta }\end{array}$
  ::对等身份:csc_1sin_sec_1cos_1cos_1cot_1tan_

  播放段落

  Other identities involve the tangent, variations on the , phase shifts, and negative angles. We will discover them in this concept.
  ::其他身份涉及相切、相异、相异、阶段变化和负面角度。我们会在这个概念中发现它们。

  播放段落

  We know that  $\begin{array}{r}\tan \theta =\frac{opposite}{adjacent}\end{array}$ . Let's show that $\begin{array}{r}\tan \theta =\frac{\sin \theta }{\cos \theta }\end{array}$ . This is the Tangent Identity .
  ::我们都知道那个塔尼欧对面的相邻点。让我们来展示一下塔尼欧的相邻点。这是坦尼欧的特征。

  播放段落

  Whenever we are trying to verify, or prove, an identity, we start with the statement we are trying to prove and work towards the desired answer. In this case, we will start with $\begin{array}{r}\tan \theta =\frac{\sin \theta }{\cos \theta }\end{array}$ and show that it is equivalent to $\begin{array}{r}\tan \theta =\frac{opposite}{adjacent}\end{array}$ . First, rewrite in terms of the ratios of the sides.
  ::每当我们试图核实或证明身份时,我们首先要从我们试图证明和努力达到理想答案的声明开始。 在这种情况下,我们首先要从Tansincos开始,并表明它相当于tanpositeadjearcent。 首先,重写两边的比例。

  播放段落

  $$\begin{array}{rl}\tan \theta & =\frac{\sin \theta }{\cos \theta }\\ & =\frac{\frac{opposite}{hypotenuse}}{\frac{adjacent}{hypotenuse}}\end{array}$$

  
  :c) 近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近似近近似近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近近

  播放段落

  Then, rewrite the complex fraction as a division problem and simplify.
  ::然后,重写复杂的碎片作为一个分裂问题,并简化。

  播放段落

  $$\begin{array}{rl}& =\frac{opposite}{hypotenuse}÷\frac{adjacent}{hypotenuse}\\ & =\frac{opposite}{\cancel{hypotenuse}}\cdot \frac{\cancel{hypotenuse}}{adjacent}\\ & =\frac{opposite}{adjacent}\end{array}$$

  
  ::在对面的近地点的近地点的近地点的近地点的近地点的近地点

  播放段落

  We now have what we wanted to prove and we are done. Once you verify an identity, you may use it to verify other identities.
  ::一旦你核实了身份,你就可以用它来验证其他身份。

  播放段落

  Now, let's show that $\begin{array}{r}{\sin }^2\theta +{\cos }^2\theta =1\end{array}$ is a true identity.
  ::现在,让我们来证明,sin2 -cos2 -1 是一个真实的身份。

  播放段落

  Change the sine and cosine in the equation into the ratios. In this problem, we will use $\begin{array}{r}y\end{array}$ as the opposite side, $\begin{array}{r}x\end{array}$ is the adjacent side, and $\begin{array}{r}r\end{array}$ is the hypotenuse (or radius), as in the unit circle .
  ::将方程中的正弦和正弦修改为比率。 在此问题上, 我们将使用 y 作为对面的一面, x 是相邻的一面, r 是下限( 半径) , 如单位圆 。

  播放段落

  $$\begin{array}{rl}{\sin }^2\theta +{\cos }^2\theta & =1\\ {\left(\frac{y}{r}\right)}^2+{\left(\frac{x}{r}\right)}^2& =1\\ \frac{y^2}{r^2}+\frac{x^2}{r^2}& =1\\ \frac{y^2+x^2}{r^2}& =1\end{array}$$

  
  :yr)2+(xr)2=1y2r2+x2r2=1y2+x2r2=1y2+x2r2=1

  播放段落

  Now, $\begin{array}{r}{x}^2+y^2=r^2\end{array}$ from the Pythagorean Theorem. Substitute this in for the numerator of the fraction.
  ::现在, x2+y2=r2 来自 Pythagorena 定理。 将其替换为分数的分子 。

  播放段落

  $$\begin{array}{r}\frac{r^2}{r^2}=1\end{array}$$

  
  ::r2r2=1

  播放段落

  This is one of the and very useful.
  ::这是非常有用的其中之一。

  播放段落

  Finally, let's verify that $\begin{array}{r}\sin \left(\frac{\pi }{2}-\theta \right)=\cos \theta \end{array}$ by using the graphs of the functions.
  ::最后,让我们使用函数的图表来验证 sin(2)=cos。

  播放段落

  The function $\begin{array}{r}y=\sin \left(\frac{\pi }{2}-x\right)\end{array}$ is a phase shift of $\begin{array}{r}\frac{\pi }{2}\end{array}$ of the sine curve.
  ::函数 y=sin( 2- x) 是正弦曲线 2 的相位移动 。

  

  播放段落

  The red function above is $\begin{array}{r}y=\sin x\end{array}$ and the blue is $\begin{array}{r}y=\cos x\end{array}$ . If we were to shift the sine curve $\begin{array}{r}\frac{\pi }{2}\end{array}$ , it would overlap perfectly with the cosine curve, thus proving this Cofunction Identity .
  ::上面的红色函数是 y=sinx,蓝色函数是 y=cosx。如果我们移动正弦曲线 2, 它会与余弦曲线完全重叠, 从而证明此函数特性 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to prove the identity of  $\begin{array}{r}\cos (-\theta )=\cos \theta \end{array}$  without graphing. 
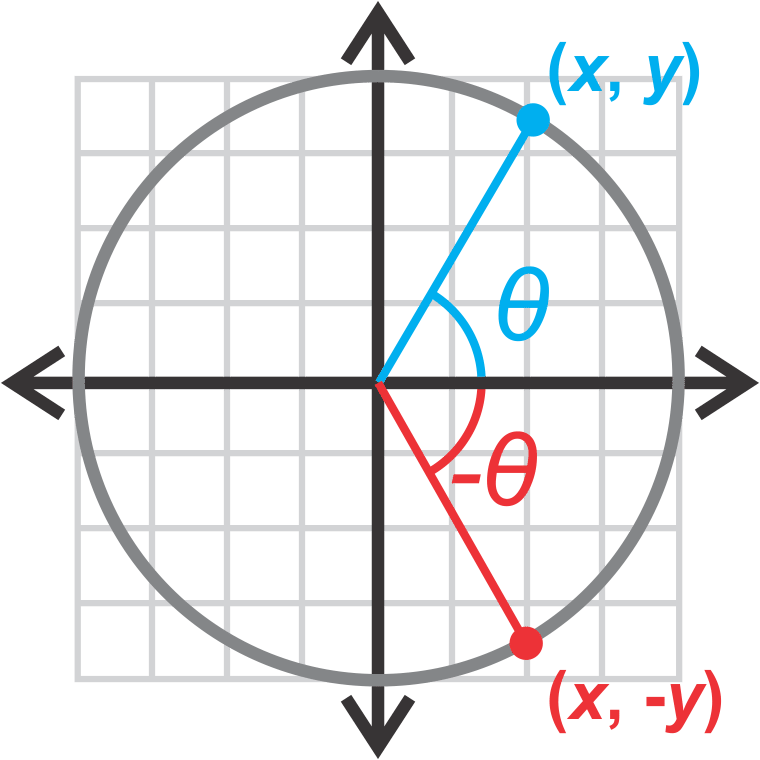
  ::早些时候,你被要求证明 COS()=COS() 的身份,而没有图形化。

  播放段落

  First, recall that $\begin{array}{r}\cos \theta =x\end{array}$ , where $\begin{array}{r}(x,y)\end{array}$ is the endpoint of the terminal side of $\begin{array}{r}\theta \end{array}$ on the unit circle.
  ::首先,请记住,Cosx,其中(x,y)是 __ 的终点端在单位圆上。

  播放段落

  Now, if we have $\begin{array}{r}\cos (-\theta )\end{array}$ , what is its endpoint? Well, the negative sign tells us that the angle is rotated in a clockwise direction, rather than the usual counter-clockwise. If we make this rotation, we see that $\begin{array}{r}\cos (-\theta )=x\end{array}$ as well, as illustrated in the following diagram.
  ::现在,如果我们有Cos(),它的终点是什么?那么,负信号告诉我们,角度是顺时针方向旋转的,而不是通常的反时针方向旋转的。如果我们进行这种旋转,我们可以看到Cos()=x,如下图所示。

  

  播放段落

  We know that $\begin{array}{r}x=x\end{array}$ , so we can set the two expressions equal to one another.
  ::我们知道 x=x, 所以我们可以设置两个等同的表达式 。

  播放段落

  $\begin{array}{r}\cos \theta =\cos (-\theta )\end{array}$
  :) ()

  播放段落

  We can now flip this identity around to get:
  ::我们现在可以翻转这个身份 来获得:

  播放段落

  $\begin{array}{r}\cos (-\theta )=\cos \theta \end{array}$
  ::cos() =cos() =cos() =cos()

  播放段落

  Example 2
  ::例2

  播放段落

  Prove the Pythagorean Identity: $\begin{array}{r}1+{\tan }^2\theta ={\sec }^2\theta \end{array}$ .
  ::证明毕达哥里人的身份: 1+tan2sec2。

  播放段落

  First, let’s use the Tangent Identity and the Reciprocal Identity to change tangent and secant in terms of sine and cosine.
  ::首先,让我们使用“长相身份”和“对等身份”来改变正弦和顺弦。

  播放段落

  $$\begin{array}{rl}1+{\tan }^2\theta & ={\sec }^2\theta \\ 1+\frac{{\sin }^2\theta }{{\cos }^2\theta }& =\frac{1}{{\cos }^2\theta }\end{array}$$

  
  ::1+tan2sec21+sin2cos21cos222222

  播放段落

  Now, change the 1 into a fraction with a base of $\begin{array}{r}{\cos }^2\theta \end{array}$ and simplify.
  ::现在,将 1 转换成一个分数, 以 com2++++ 为基础, 并简化 。

  播放段落

  $$\begin{array}{rl}1+\frac{{\sin }^2\theta }{{\cos }^2\theta }& =\frac{1}{{\cos }^2\theta }\\ \frac{{\cos }^2\theta }{{\cos }^2\theta }+\frac{{\sin }^2\theta }{{\cos }^2\theta }& =\frac{1}{{\cos }^2\theta }\\ \frac{{\cos }^2\theta +{\sin }^2\theta }{{\cos }^2\theta }& =\frac{1}{{\cos }^2\theta }\\ \frac{1}{{\cos }^2\theta }& =\frac{1}{{\cos }^2\theta }\end{array}$$

  
  ::1+sin2cos21cos2cos2cos2sin2cos21cos2cos2cos2cos2cos221cos21cos21cos21cos21cos21cos221cos22221cos221cos2222cos22cos2cos22cos22cos2cos22cos2cos22cos2cos22cos2cos2cos2cos22cos222c222c222222222222222222222222222222

  播放段落

  In the second to last step, we arrived at the original Pythagorean Identity $\begin{array}{r}{\sin }^2\theta +{\cos }^2\theta \end{array}$ in the numerator of the left-hand side. Therefore, we can substitute in 1 for this and the two sides of the equation are the same.
  ::在最后一步的第二步中,我们到达了左侧分子中最初的“毕达哥里安身份”sin2cos2。因此,我们可以以1取代这一边,而等式的两面是相同的。

  播放段落

  Example 3
  ::例3

  播放段落

  Without graphing, show that $\begin{array}{r}\sin (-\theta )=-\sin \theta \end{array}$ .
  ::没有图形化,请显示 sin()sin()sin() 。

  播放段落

  First, recall that $\begin{array}{r}\sin \theta =y\end{array}$ , where $\begin{array}{r}(x,y)\end{array}$ is the endpoint of the terminal side of $\begin{array}{r}\theta \end{array}$ on the unit circle.
  ::首先,请记住,siny, 其中(x,y) 是 __ 的终点端在单位圆上。

  播放段落

  Now, if we have $\begin{array}{r}\sin (-\theta )\end{array}$ , what is it’s endpoint? Well, the negative sign tells us that the angle is rotated in a clockwise direction, rather than the usual counter-clockwise. By looking at the picture, we see that $\begin{array}{r}\sin (-\theta )=-y\end{array}$ . Therefore, if $\begin{array}{r}\sin \theta =y\end{array}$ , then $\begin{array}{r}-\sin \theta =-y\end{array}$ and combining the equations, we have $\begin{array}{r}\sin (-\theta )=-\sin \theta \end{array}$ .
  ::现在,如果我们有sin {{{{{}},它的终点是什么?嗯,负信号告诉我们,这个角度是按时针方向旋转的,而不是通常的反时针方向旋转的。看一看这个图片,我们就会看到这个角度。因此,如果是 sin},那么-siny 和 组合方程式,我们就有了 sin}{{}{{}}{sin}}。

  

  播放段落

  Review
  ::回顾

  播放段落
  1. Show that $\begin{array}{r}\cot \theta =\frac{\cos \theta }{\sin \theta }\end{array}$ .
     ::显示那个小鸡鸡。
  播放段落
  2. Show that $\begin{array}{r}\tan \theta =\frac{\sec \theta }{\csc \theta }\end{array}$ .
     ::显示塔纳塞卡。
  播放段落
  3. Show that $\begin{array}{r}1+{\cot }^2\theta ={\csc }^2\theta \end{array}$ .
     ::显示 1+cot2csc2。
  播放段落
  4. Explain why $\begin{array}{r}\cos \left(\frac{\pi }{2}-\theta \right)=\sin \theta \end{array}$ by using the graphs of the two functions.
     ::使用两个函数的图形来解释为什么 cos( 2) =sin( sin) 。
  播放段落
  5. Show that $\begin{array}{r}\sec (-\theta )=\sec \theta \end{array}$ .
     ::显示 sec =sec 。
  播放段落
  6. Explain why $\begin{array}{r}\tan (-\theta )=-\tan \theta \end{array}$ is true, using the Tangent Identity and the other Negative Angle Identities.
     ::解释为何Tan()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()(()()()()()()琌痷痷龟 ノ(()()(())(()(()() ) (() ) ((() ) (() ) (((()琌)琌琌琌琌)琌琌琌琌琌痷))琌琌琌 (((() () (())琌 ()琌痷)琌痷)琌痷)琌琌痷

  播放段落

  Verify the following identities.
  ::验证以下身份 。

  播放段落
  7. $\begin{array}{r}\cot \theta \sec \theta =\csc \theta \end{array}$
     ::
  播放段落
  8. $\begin{array}{r}\frac{\cos \theta }{\cot \theta }=\frac{\tan \theta }{\sec \theta }\end{array}$
     ::
  播放段落
  9. $\begin{array}{r}\sin \theta \csc \theta =1\end{array}$
     ::性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别 性别
  播放段落
  10. $\begin{array}{r}\cot (-\theta )=-\cot \theta \end{array}$
      :) () () () () () () () () () ()
  播放段落
  11. $\begin{array}{r}\tan x\csc x\cos x=1\end{array}$
      ::tanxcscxcosx=1 NAME OF TRANSLATORS
  播放段落
  12. $\begin{array}{r}\frac{{\sin }^2\left(-x\right)}{{\tan }^{2}x}={\cos }^{2}x\end{array}$
      :- x)tan2\\\\ x=cos2\\\ x

  播放段落

  Show that $\begin{array}{r}{\sin }^2\theta +{\cos }^2\theta =1\end{array}$ is true for the following values of $\begin{array}{r}\theta \end{array}$ .
  ::显示 sin2cos21 对以下的 __ 值是真实的 。

  13. $\begin{array}{r}\frac{\pi }{4}\end{array}$
  14. $\begin{array}{r}\frac{2\pi }{3}\end{array}$
  15. $\begin{array}{r}-\frac{7\pi }{6}\end{array}$
  播放段落
  16. Recall that a function is odd if $\begin{array}{r}f(-x)=-f(x)\end{array}$ and even if $\begin{array}{r}f(-x)=f(x)\end{array}$ . Which of the six trigonometric functions are odd? Which are even?
      ::回顾如果 f(- x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。